地震作用下地铁隧道与邻近建筑相互影响研究

卢致强 曹 平 李冀伟 刘建伟

(中铁隆工程集团有限公司,610045,成都//第一作者,高级工程师)

地震作用下地铁隧道与邻近建筑相互影响研究

卢致强 曹 平 李冀伟 刘建伟

(中铁隆工程集团有限公司,610045,成都//第一作者,高级工程师)

以西安地铁某区间隧道侧穿学校公寓为研究对象,利用MIDAS GTS数值模拟软件进行时程分析。重点研究了地震作用下地铁隧道与邻近建(构)筑物间的相互影响。研究结果表明,隧道结构刚度较周围地层大,对周围地层变形存在约束性,使隧道周围地层的整体刚度有所提高,隧道结构的修建不会造成周围地层及邻近建筑所受地震作用增大,而邻近建筑的存在会造成隧道结构所受的地震作用增大。根据研究结果,针对隧道邻近建(构)筑物提出了抗震构造措施,为类似工程提供参考。

地铁隧道; 邻近建筑; 地震作用; 时程分析; 数值模拟

Author′s address Ranken Railway Construction Group Co.,Ltd.,610045,Chengdu,China

我国地处欧亚地震带和环太平洋地震带之间,地震活动频繁,是世界上最大的大陆浅源强震活动区,而大量的隧道工程位于高地震烈度区[1]。地下结构由于受到地层的约束,加之城市隧道大多采用抗震性能较好的整体现浇钢筋混凝土结构及能够适应地层变形的装配式圆形结构,震害明显低于地上结构[2]。但高烈度地震区内的地铁大规模建设是在近些年才出现的,大多数还没有经过大地震的检验,因此灾难性的震害记录不多。1995年日本阪神大地震中,神户市地铁车站及区间隧道遭到严重破坏,引起了众多地震工作者的高度重视。随着城市地铁建设的发展及某些地区地铁震害的出现,我国于2014年12月1日开始实施GB 50909—2014《城市轨道交通结构抗震设计规范》,规定抗震设防地区的城市轨道交通结构必须进行抗震设计[2]。城市轨道交通作为国家生命线工程之一,必须对其抗震计算给予高度重视。

在城市繁华地区或一些特定地段,由于受既有建(构)筑物、地质条件的限制及地下空间综合开发、利用的需要,地铁隧道与其它结构物间的距离变得越来越小。地震作用下,地铁与邻近建(构)筑物相互影响的研究成为一个不容忽视的课题。根据住房和城乡建设部颁布的《市政公用设施抗震设防专项论证技术要点(地下工程篇)》,需要对地下结构沿线的地震风险源进行风险判定及评估。但国内外对于地震作用下地下结构与邻近建(构)筑物相互影响的研究极少,亟待深入和完善指导实际工程的理论和技术。目前,岩土工程数值模拟技术已非常成熟,不仅可模拟地层及隧道衬砌结构,而且可输入地震时程,较为真实地模拟地震作用。本文利用MIDAS GTS数值分析软件,针对西安地铁某区间隧道侧穿学校公寓进行数值模拟,并结合既有工程经验及相关规范,分析地震作用下地铁隧道与邻近建筑的相互影响,提出有效的抗震措施。

1 工程及地质概况

1.1 工程概况

邻近建筑公寓为5层砖混结构,筏板基础,基础埋深约2 m。地铁区间隧道自该建筑南侧穿过。隧道与该楼最小水平距离约4.1 m,最小竖向距离约8.5 m。地铁区间为左右分建的两条单洞单线隧道,断面为马蹄形,内净空为8.3 m (宽)×8.45 m (高);二衬采用C35混凝土,厚度0.5 m;左右线线间距约为15 m;隧道埋深约10.5 m。区间隧道与该公寓位置关系如图1、2所示。

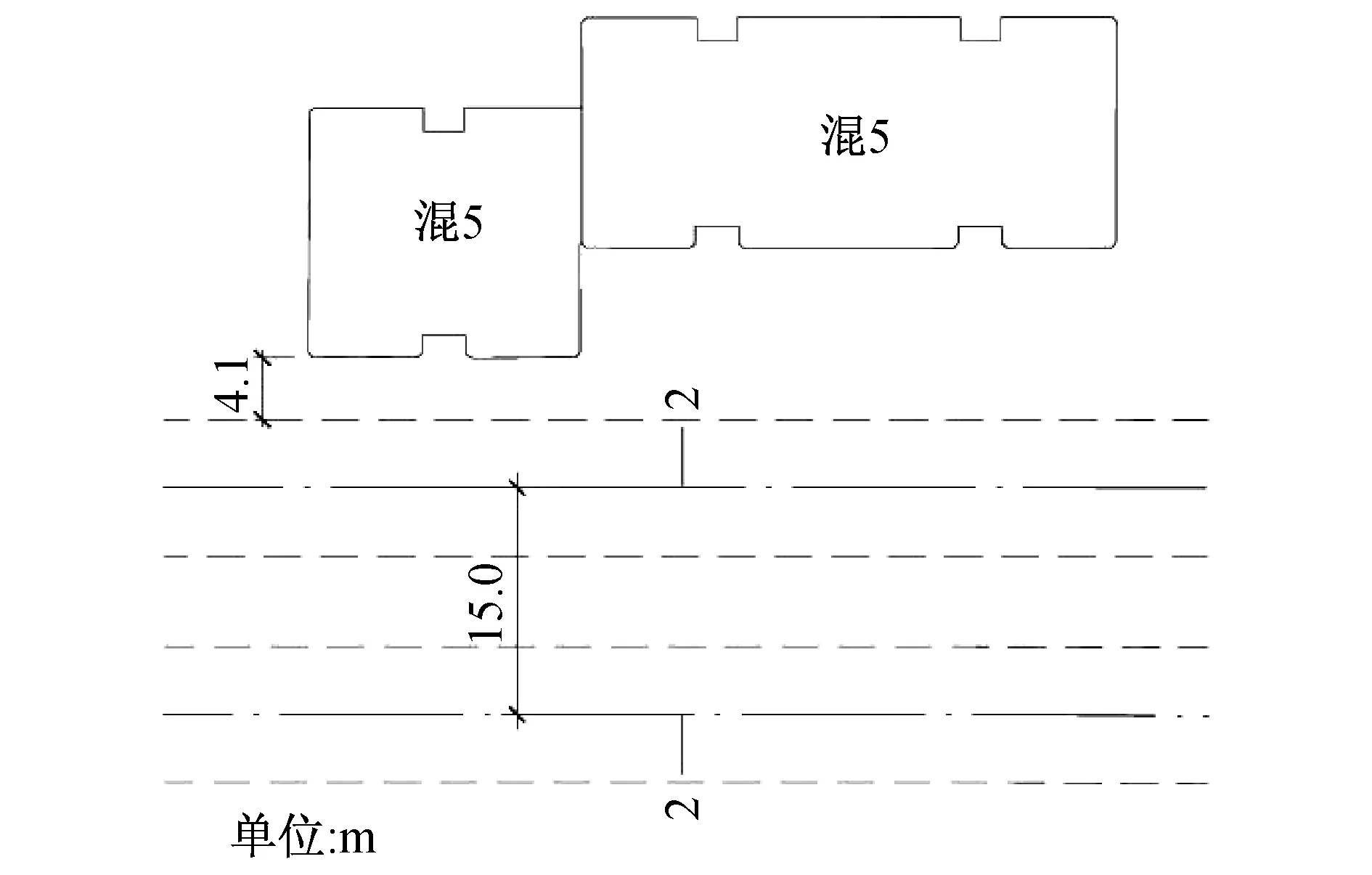
图1 区间隧道与公寓水平位置关系图

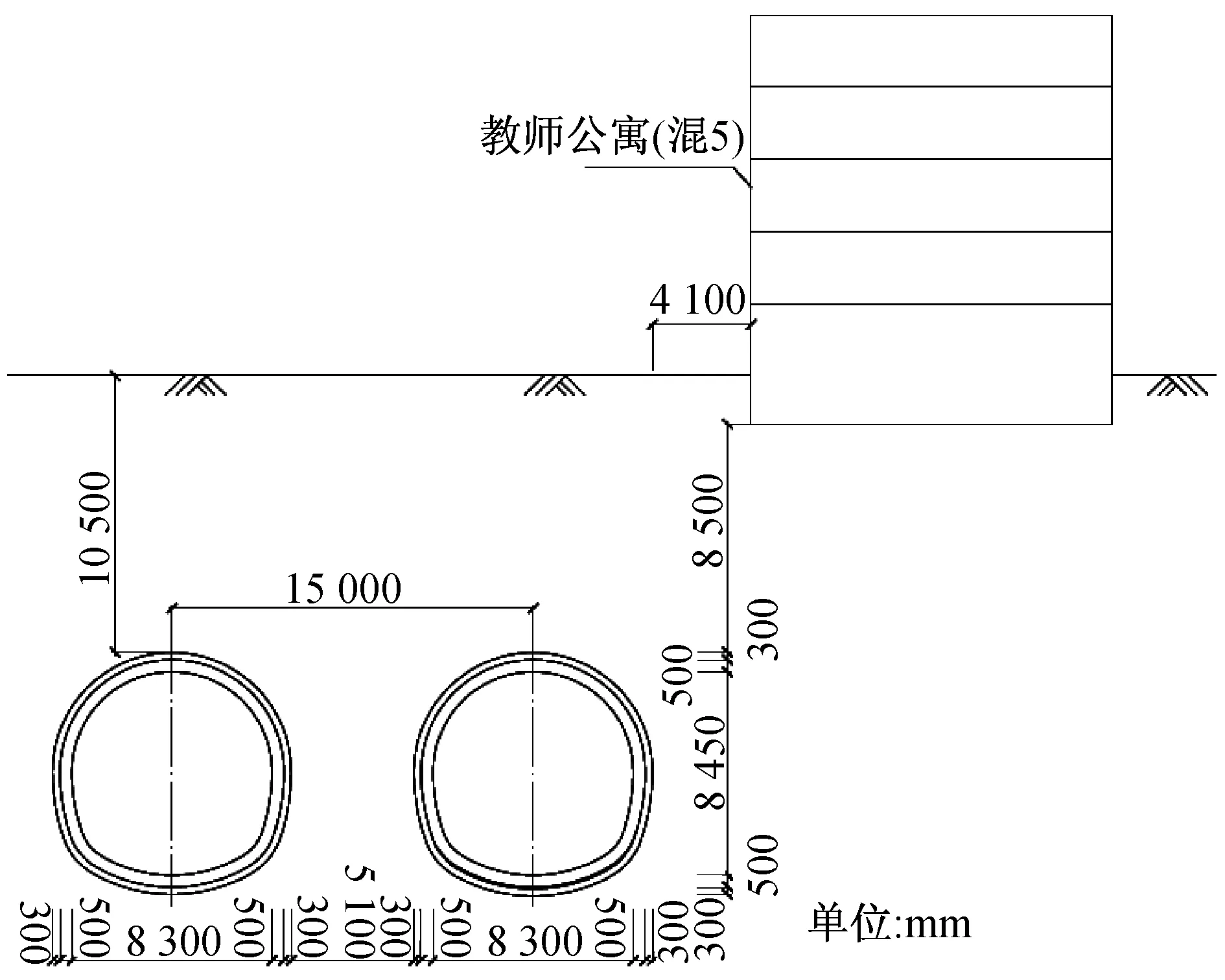
图2 区间隧道与公寓竖向位置关系图

1.2 地质概况

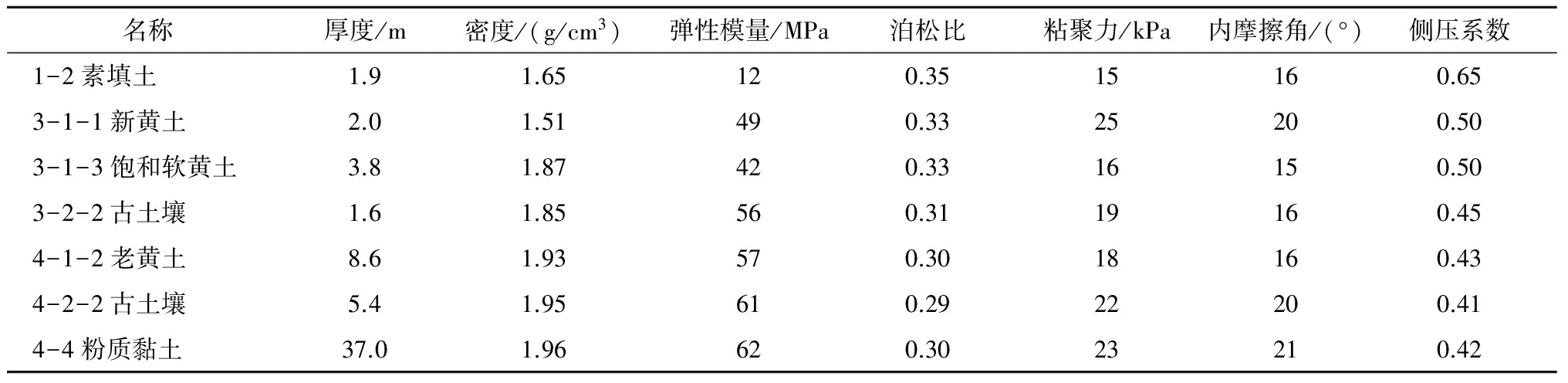
表1 土层和材料参数

模拟时所采用的动弹性模量可根据《岩土工程勘察规范》由剪切波速、压缩波速及土的质量密度进行计算得到。本文模拟时采用的动弹性模量根据勘察报告,按西安地区经验取弹性模量的10倍。

2 计算模型及输入

2.1 模型的建立

计算采用地层-结构模型进行时程分析。该分析把地震运动视为一个随时间变化的过程,并将地下结构物和周围土体介质视为共同受力变形的整体,通过直接输入地震时程,在满足变形协调的前提下,分别计算结构物和土体介质在各个时刻的位移、速度、加速度、应变及内力等,以验算场地的稳定性以及隧道结构和邻近建筑的抗震性能。

模型计算采用MIDAS GTS软件进行时程分析。动力有限元数值分析中,为保证计算精度及控制频散、提高截止频率,要求集中质量有限元单元尺寸与关注的最小波长之比不大于1/6。在模拟的波长内包含6～8个数目的单元长度,将有较高的精度。因此在对建立的有限元分析模型进行网格划分时,所关心振动波的高频(短波)成分决定网格单元尺寸,低频(长波)成分决定模型边界范围的大小[3]。根据《城市轨道交通结构抗震设计规范》,采用动力分析时,由于直接输入地震波作用,限制土层单元尺寸时,通常竖向单元尺寸不大于1 m即可满足要求;对于模型尺寸,计算模型的侧面人工边界距离地下结构的距离不小于3倍地下结构水平有效宽度,底面取至设计地震作用的基准面且距离结构不小于3倍地下结构竖向有效高度,上表面取至实际地表。

对于有限的计算区域,在地震激励下,波动能量将在人工截取的边界上发生反射,使波发生震荡,导致模拟失真[4]。为解决有限模型边界上波的反射问题,《城市轨道交通结构抗震设计规范》规定模型边界一般采用粘性或粘弹性人工边界。粘弹性边界不仅可较好地模拟地基的辐射阻尼,而且能模拟远场地球介质的弹性恢复性能,具有良好的低频稳定性[5]。本文计算模型采用集中粘弹性人工边界,即在有限元模型中任一人工边界节点的法向和切向分别设置并联的弹簧单元和阻尼器单元[6-7]。在MIDAS GTS中通过输入基床系数及阻尼,实现粘弹性人工边界的加载。

综上,所建立模型尺寸长133.4 m,高76.2 m。模拟时,地层采用平面单元,邻近建筑按质量等效为平面单元。模型地表面为自由面,周边采用粘弹性人工边界。计算中土体采用摩尔-库仑模型,初始应力场仅考虑土体自重应力场,不考虑地层的构造应力。

2.2 地震动时程

根据勘察报告,本场地类别为Ⅱ类。场地土类型为中软～中硬土。拟建场地位于抗震设防烈度8度区内,地震动峰值加速度值amax为0.20g,设计地震分组为第一组。场地类别为Ⅱ类的地震动反应谱特征周期为0.35 s。

本场地土类型为中硬土,场地类别为Ⅱ类场地。本区间计算采用50年超越概率为10%的基岩加速度反应谱和峰值加速度作为地震动时程合成的目标峰值和反应谱,采用三角级迭代法合成土层地震反应分析所需的基岩地震动时程。地震动时程数据如表2所示。地震动时程曲线如图3所示。

表2 地震动时程数据

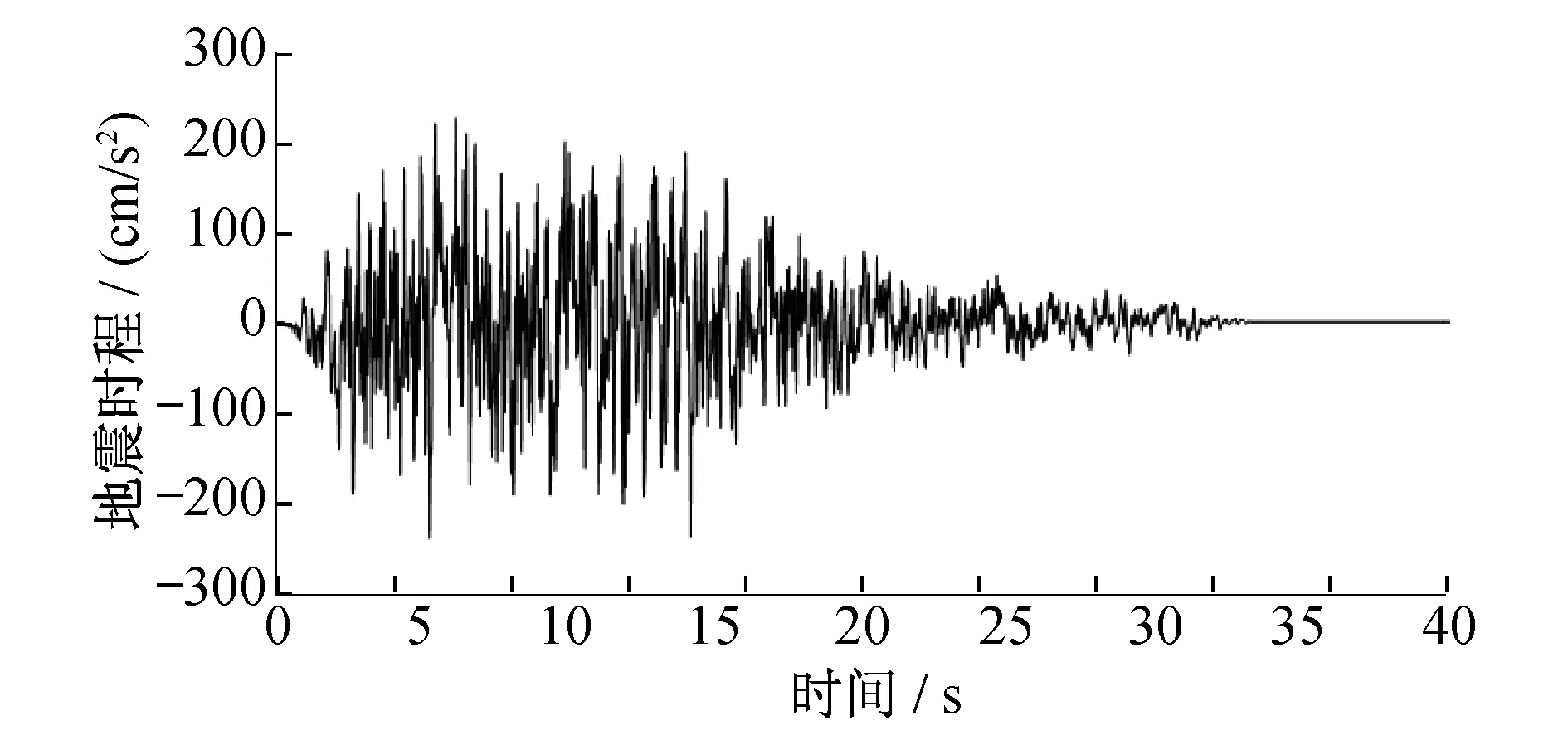
图3 50年超越概率10%基岩水平地震动时程图

2.3 计算工况

分别针对工况1、2、3进行模拟分析,通过三种工况对比,分析地铁隧道与邻近建筑抗震性能的相互影响。

工况1:未修建地铁隧道,存在邻近建筑(见图4);

工况2:修建地铁隧道,存在邻近建筑(见图5);

工况3:修建地铁隧道,无邻近建筑(见图6)。

3 数值模拟结果及分析

3.1 数值模拟结果

工况1计算结果如图7、8所示。由图7、8可知,地震作用时,邻近建筑顶部的最大位移为79.49 mm,发生于7.75 s;最大层间位移发生于建筑顶层,最大层间位移为3.185 mm,发生于7.45 s。

图4 工况1

图5 工况2

图6 工况3

图7 工况1时建筑顶部位移时程曲线

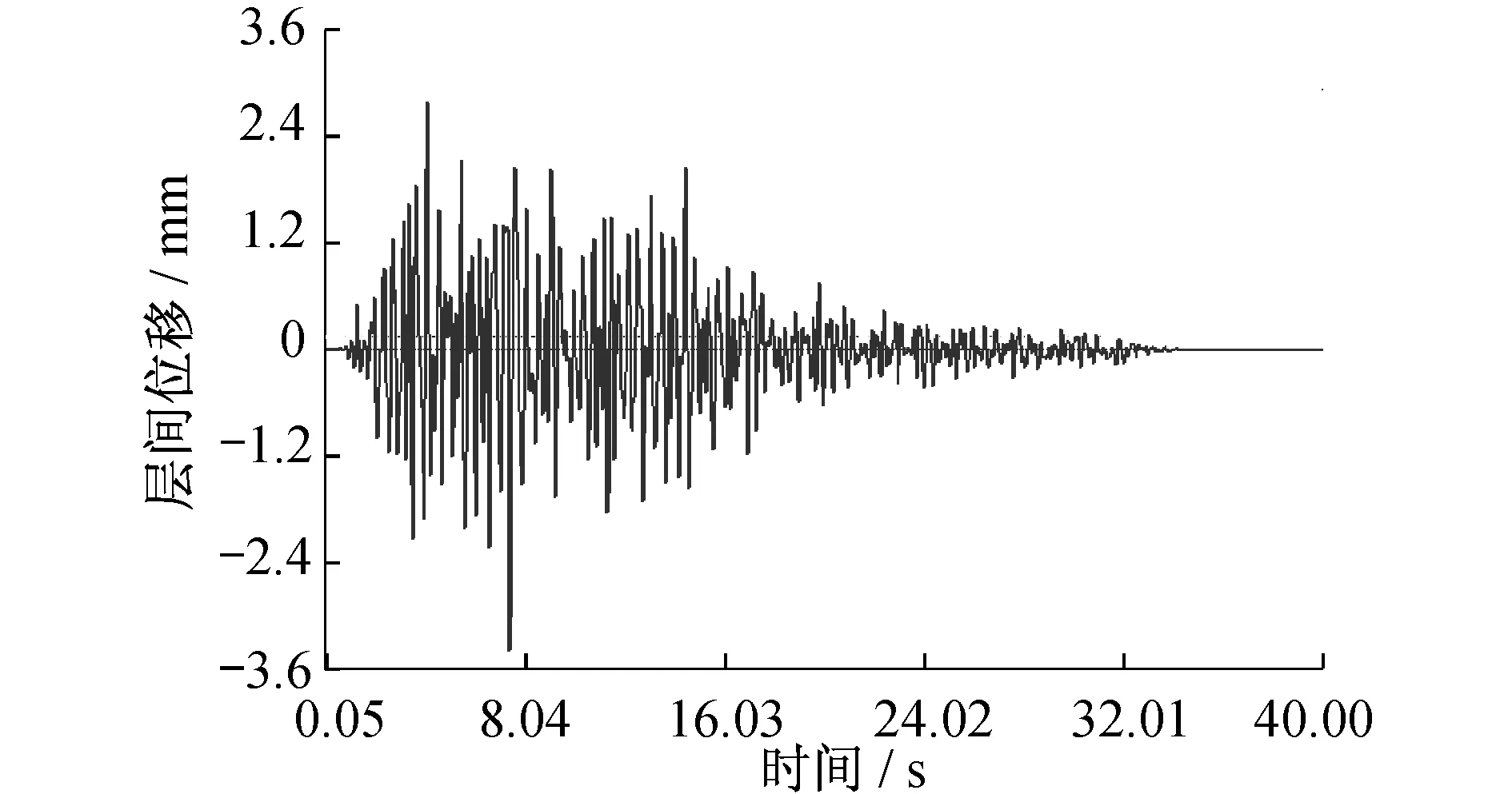
图8 工况1时层间位移时程曲线

工况2计算结果如图9～11所示。由图9、10可知,地震作用时,邻近建筑顶部的最大位移为73.51 mm,发生于7.75 s;最大层间位移发生于建筑顶层,最大层间位移为2.923 mm,发生于7.45 s。由图11可知,地震作用时,隧道顶、底的最大相对位移为2.894 mm,发生于7.45 s。

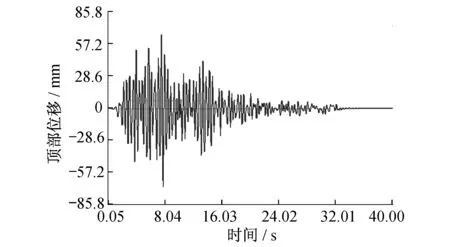
图9 工况2时建筑顶部位移时程曲线

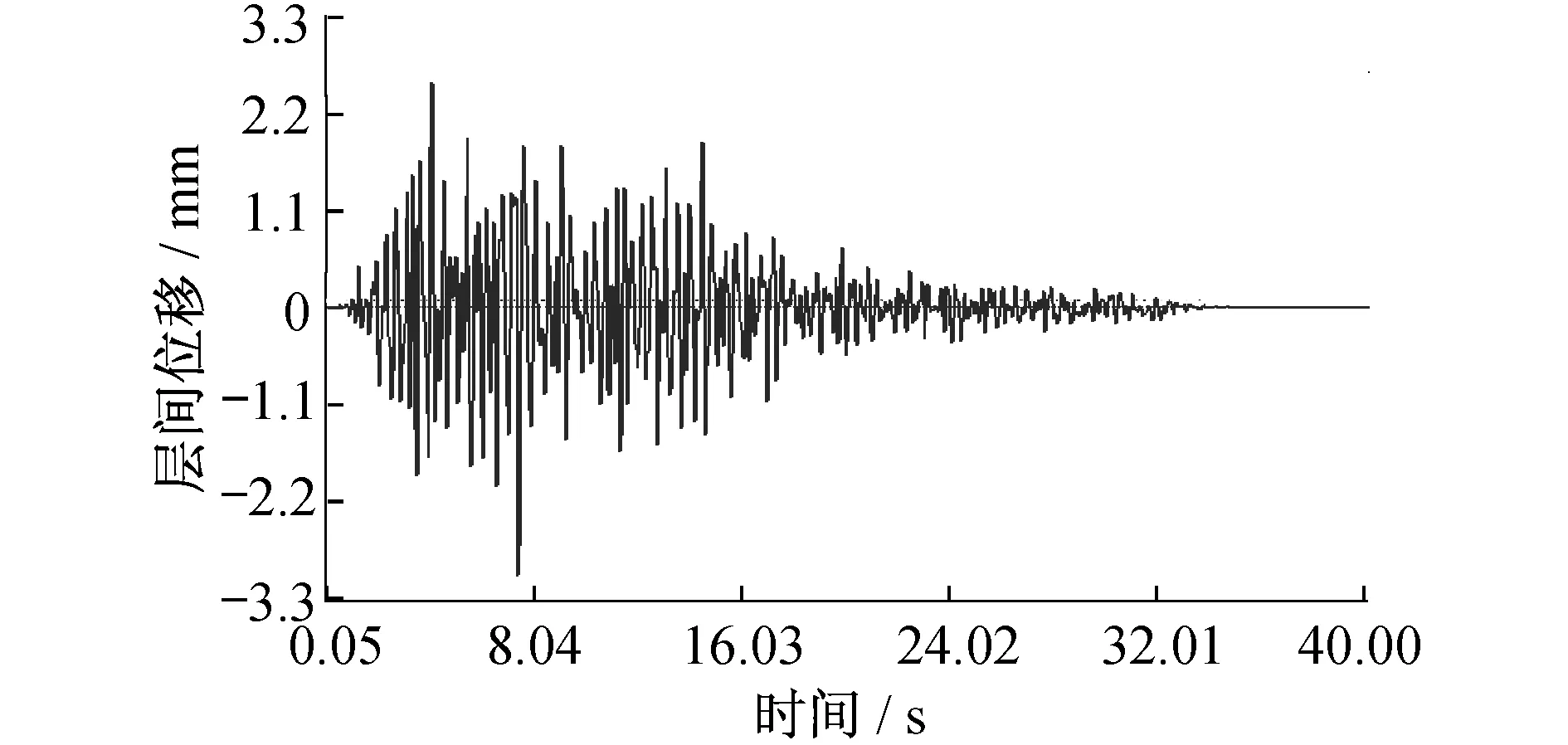
图10 工况2时层间位移时程曲线

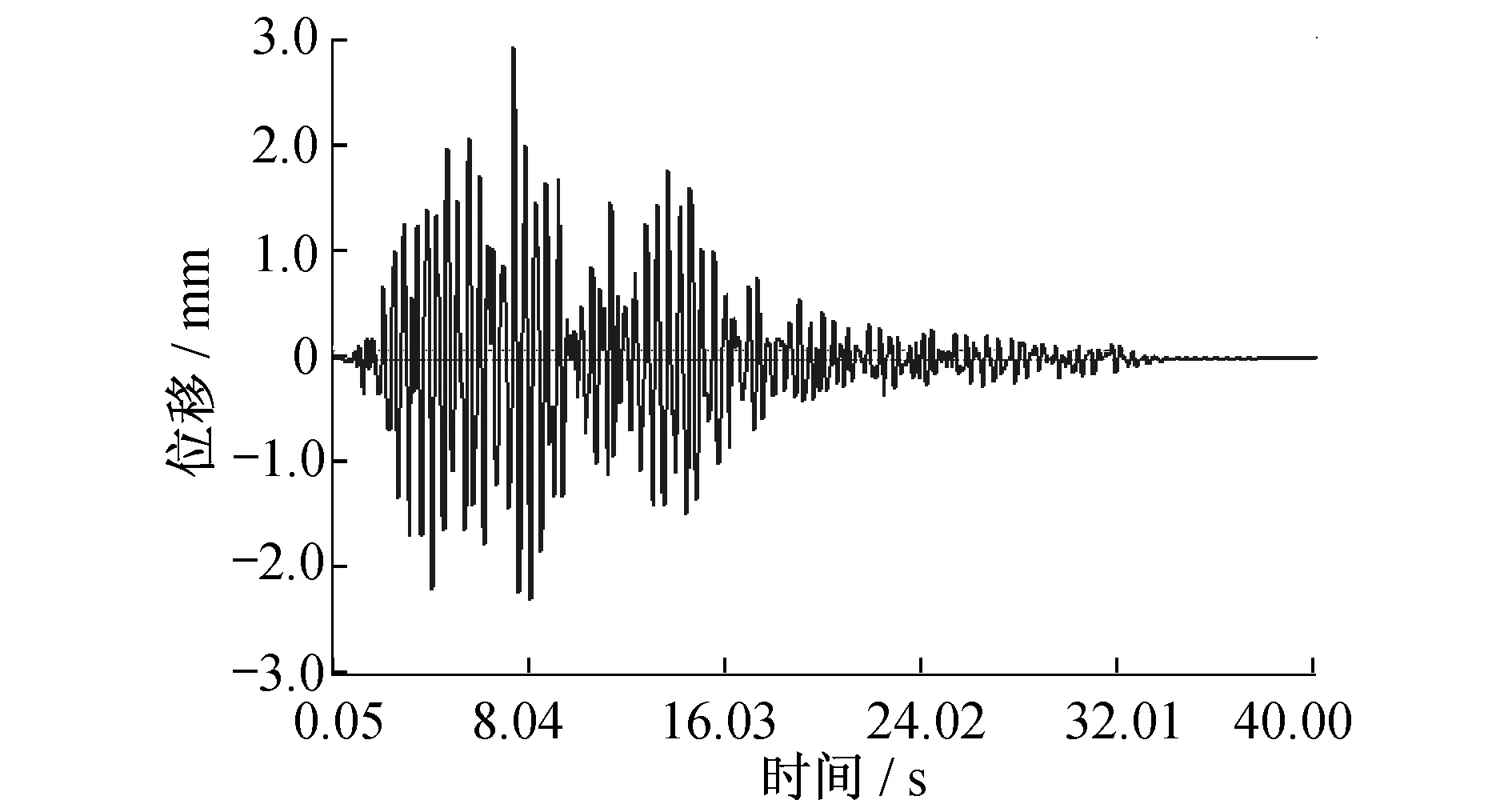
图11 工况2时隧道拱顶与拱底相对位移时程曲线

工况3计算结果如图12所示。可见,地震作用时,隧道顶、底的最大相对位移为2.486 mm,发生于7.45 s。

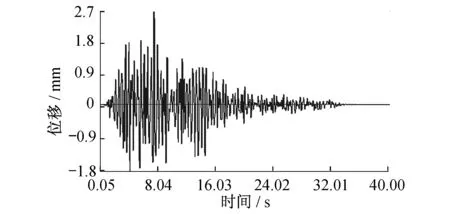
图12 工况3时隧道拱顶与拱底相对位移时程曲线

3.2 计算结果对比分析

将三种工况计算结果进行对比分析,结果如表3、4所示。

表3 工况1与工况2计算结果对比

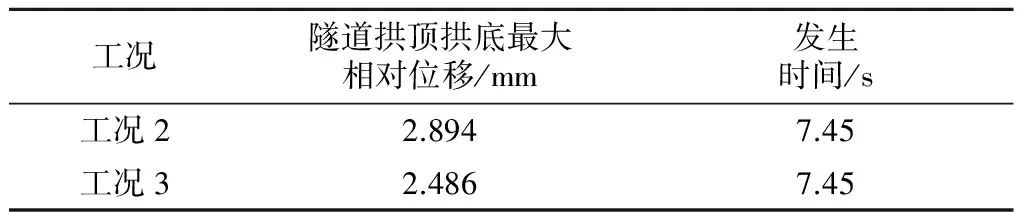
表4 工况2与工况3计算结果对比

由表3可知,工况1中邻近建筑顶部最大位移及最大层间位移均略大于工况2。即隧道修建后,在地震作用下,邻近建筑顶部的最大位移及最大层间位移均有所减小(邻近建筑顶部位移减小约7.52%,最大层间位移减小约8.23%)。

由表4可知,工况2中隧道拱顶与拱底的最大相对位移略大于工况3。即当地面存在邻近建筑时,在地震作用下,隧道拱顶与拱底最大相对位移有所增加(最大相对位移增加约16.41%)。

3.3 地震作用下地铁隧道及邻近建筑相互影响

(1) 根据表3的对比结果,修建地铁隧道后,地震作用下邻近建筑的位移有所减小,但影响程度较小。其原因在于隧道结构断面较小,其在横向和纵向上的刚度较周边地层要大,对地层的整体抗震性能有所提升,因此导致作用在临近建筑物上的地震作用有所减小。

(2) 根据表4的对比结果,当存在邻近建筑时,在地震作用下,隧道拱顶与拱底的最大相对位移有所增大,但影响程度较小。其原因在于地面建筑在时程计算过程中增加了作用在结构上的荷载(本文中地面建筑规模相对较小,其增加于结构上的荷载较小),因此导致作用在隧道结构上的地震作用有所增大。

4 结论及抗震措施

4.1 结论

(1) 综合本文中三个分析工况并结合国内外既有工程经验,隧道结构在满足自身抗震性能要求的情况下(即地震作用时结构处于弹性工作阶段或结构局部进入弹塑性工作阶段,但结构不会产生较大破坏,不会出现局部或整体倒塌),隧道结构建成后,其结构刚度较周围地层大,对周围地层变形存在约束性,使隧道周围地层的整体刚度有所提高,整体抗震性能提高,从而使邻近建筑所受地震作用有所降低。

(2) 本文中隧道结构埋深较大,断面较小,邻近建筑荷载对其影响较小;且结构强度、变形及裂缝等计算时已考虑邻近建筑位置及其荷载的影响,结构厚度及配筋满足相关要求。考虑到周围地层对隧道结构的约束作用,地震作用时,邻近建筑的存在导致隧道结构所受地震作用增强。

(3) 地震作用下隧道结构与邻近建筑的相互影响较小。地震作用下隧道与邻近建筑之间的相互影响与隧道结构尺寸及建(构)筑物的规模有关,同时与隧道结构和建(构)筑物之间的位置关系有关,隧道结构与邻近建(构)筑物抗震的相互影响中隧道结构尺寸及断面形式的优化分析是个值得进一步研究的问题。

4.2 隧道邻近建(构)筑物段抗震措施

(1) 隧道结构强度、变形及裂缝宽度等计算应考虑邻近建(构)筑物位置及荷载的影响,必要时对结构进行加强,以保证隧道结构修建后不会降低周围地层的整体刚度。

(2) 严格控制施工质量,避免人为因素产生隧道结构的薄弱点。钢筋的焊接、绑扎及锚固等应满足抗震相关要求。

(3) 对盾构法和矿山法施工的隧道结构,应及时向衬砌背后压注结硬性浆液,保证周围围岩和隧道结构的共同作用。

(4) 对于抗震薄弱部位必要时可以采取如下措施:①在适当距离设置减震缝,并充填软质减震材料;②在隧道周围一定范围内对围岩进行注浆加固;③在衬砌与围岩间设置板式减震层或压注减震材料;④衬砌结构采用钢纤维混凝土(增加强度)或采用聚合物混凝土(增加阻尼)。

[1] 耿萍,张景,何川,等. 隧道横断面反应位移法基本原理及其应用[J]. 岩石力学与工程学报,2013,32(增2):3478-3485.

[2] 中华人民共和国住房和城乡建设部.城市轨道交通结构抗震设计规范:GB 50909—2014[S].北京:中国计划出版社,2014:28-39.

[3] 李金明.高速铁路高架线路列车运行对既有地面线振动影响[D]. 北京:北京交通大学,2012.

[4] 陈万祥,郭志坤,袁正如,等. 地震分析中的人工边界及其在LS_DYNA中的实现[J]. 岩石力学与工程学报,2009,28(增2):3504-3515.

[5] 王祥秋,杨林德,周治国.列车振动荷载作用下隧道衬砌结构动力响应特性分析[J]. 岩石力学与工程学报,2006,25(7):1337-1342.

[6] 李彬.地铁地下结构抗震理论分析与应用研究[D].北京:清华大学,2005.

[7] 刘晶波,李彬.地铁地下结构抗震分析及设计中的几个关键问题[J]. 岩土木工程学报,2006,39(6):106-100.

On the Mutual Effects of Earthquake Action on Subway Tunnels and the Adjacent Buildings

LU Zhiqiang, CAO Ping, LI Jiwei, LIU Jianwei

Taking a section tunnel crossing alongside the university apartment as the case,MIDAS GTS numerical simulation software is used to take a time-history analysis,the mutual effects of subway tunnels and the adjacent buildings under earthquake action are mainly studied.The result of this research shows that tunnel structure is characterized by greater stiffness than that of the surrounding strata,which exerts certain binding force on the stratum deformation.At the same time,the tunnel will strengthen the stiffness of the surrounding strata,but not increase the earthquake action on the surrounding strata and the surrounding buildings.To the contrary,the surrounding buildings will increase the earthquake action on tunnel structure.Based on this study,the seismic structural measures of the buildings adjacent to tunnels are proposed,so as to provide a reference for similar projects.

subway tunnel; adjacent building; earthquake action; time-history analysis; numerical simulation

U452.2+8:U231

10.16037/j.1007-869x.2017.04.010

2015-07-15)