整备状态下的轨道交通车辆车体模态计算分析*
赵士忠 王晋乐 朱 涛
(1.中车青岛四方机车车辆股份有限公司,266111,青岛;2.西南交通大学牵引动力国家重点实验室,610031,成都//第一作者,高级工程师)
整备状态下的轨道交通车辆车体模态计算分析*
赵士忠1王晋乐1朱 涛2
(1.中车青岛四方机车车辆股份有限公司,266111,青岛;2.西南交通大学牵引动力国家重点实验室,610031,成都//第一作者,高级工程师)
推导了多自由度刚体振动系统振动频率和特征向量的解析方法,研究了轨道交通车辆车体设备悬挂方式及其垂向悬挂刚度与车体系统振动频率和车体各阶振幅之间的关系。以某轨道交通车辆车体模态分析为例,对车体模态分析过程中悬挂设备的模拟方法、车体内装和设备的刚度,以及乘客质量对车体一阶垂弯和扭转频率的影响进行了深入分析和试验对比。研究结果表明,设备悬挂方式和悬挂刚度的选择对车体频率有非常显著的影响;与试验相比,考虑设备悬挂刚度、内装和设备自身刚度时对车体主要振动模态有显著提升,应在车体结构设计时予以注意;乘客质量对车体主要振动模态频率几乎没有影响。
轨道交通车辆; 车体模态分析; 振动频率解析法; 设备悬挂刚度; 内装刚度; 乘客质量
First-author′s address CRRC Qingdao Sifang Co.,Ltd.,266111,Qingdao,China
研究表明,过低的车体垂向弯曲频率会降低车体的垂向平稳性[1]。车体一阶垂直弯曲和一阶扭转频率是评价运行安全性和乘坐舒适度的重要参数,也为车体轻量化设计提供参考依据,在车辆前期设计阶段对该参数进行计算评估尤为重要。
文献[2-5]将车体结构视为有限个自由度的离散体,基于有限元法对轨道车辆整备车体进行了模态分析,车体吊挂设备采用质量均布、质量点或修改弹性模量的方法进行模拟,未考虑设备的悬挂方式(刚性或弹性)、设备自身刚度以及乘客的影响。文献[6]将车体结构等效为自由梁,建立了车体刚柔耦合运动方程,分析了弹性悬挂设备对整备车体模态的影响。文献[7]基于模态叠加法原理建立了考虑车体弹性振动和车下设备的高速动车组三维刚柔耦合动力学模型,分析了车下设备悬挂方式、重心偏载与弹性悬挂参数对车体振动响应的影响规律。然而,整备车体是由钢结构、设备、连接件,以及内装部件等组成,其系统振动不仅包含车体结构自身的刚性和弹性振动,还包含各设备的刚体振动,因此整备车体是一个刚柔耦合振动的系统。车体的各阶振动模态由车体结构的刚体振动、弹性振动以及设备的刚体振动叠加而成,所以整备车体的一阶垂弯频率不仅与车体钢结构一阶垂弯固有频率有关,还与设备的刚体悬挂频率、内装和设备刚度有关。另外,乘员质量也是影响车体设计的重要参考指标。因此,在轨道车辆车体结构设计过程中,不仅要考虑钢结构自身的振动频率,还应对影响车体模态的各种因素进行综合评估,以便快速、有效、准确地对设计的车体振动频率进行评估,使其不仅能满足整备车体抗振设计的要求,而且可避免结构刚度冗余设计带来的结构质量不必要的增加。
本文通过推导的多自由度刚体振动系统振动频率和特征向量解析方法,研究轨道交通车辆车体设备悬挂方式及其垂向悬挂刚度与车体系统振动频率和车体各阶振幅之间的关系,在此基础上,研究车体模态分析过程中悬挂设备的模拟方法、车体内装和设备的刚度,以及乘客质量对车体一阶垂弯和扭转频率的影响,希望从理论和有限元分析手段两个角度对轨道交通车辆车体模态分析关键问题进行全面解析,进而指导车体结构设计。
1 车体悬挂设备振动解析方法
1.1 多自由度刚体振动系统分析
为了研究设备悬挂方式(刚性或弹性)对车体振动频率尤其是一阶垂直弯曲的影响,将轨道交通车辆车体及其主要悬挂件(如主变压器、牵引变流器)等效为刚体,建立系统多自由度垂向振动力学模型,如图1所示。图中,Z0、Z1、Z2、Zi分别为车体、主变压器、牵引变流器及其它悬挂设备的垂向位移;m0、m1、m2、mi分别为车体、主变压器、牵引变流器及其它悬挂设备的质量,其中m0为除去橡胶件悬挂质量的车体整备状态总质量;k0、k1、k2、ki分别为车体、主变压器、牵引变流器及其它悬挂设备的垂向悬挂刚度。
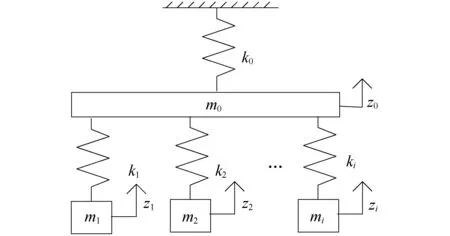
图1 多自由度车体系统垂向振动模型
k0的表达式为:
k0=(2π·f0)2·m0
(1)
式中:
f0——除去橡胶件悬挂质量的车体整备状态的一阶垂弯频率。
建立多自由度车体系统的垂向振动方程:
(2)
(3)
将上式转化为一般表达式形式:
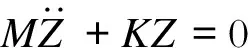
(4)
其中
则
K·Z=λ·M·Z
(5)
求解式(5)的特征根和特征向量,即可求出各部件的振动频率。
首先,对质量矩阵M进行Cholesky三角分解,即M=L·LT,式(5)变为:
L-1·K·L-T·Z=λ·Z
(6)
对L-1·K·L-T矩阵求解特征值,即可得出部件的振动频率和特征向量(振型)。
1.2 算例分析
基于某型轨道交通车辆车体相关参数,对以上理论分析进行验证。车体相关参数如表1所示。

表1 车体及悬挂参数
改变主变压器的垂向悬挂刚度,得到不同主变压器垂向悬挂刚度下的系统振动频率和车体相对振幅,如图2所示。图中,相对振幅高的振型为主振型,此时对应的频率为主振型频率。
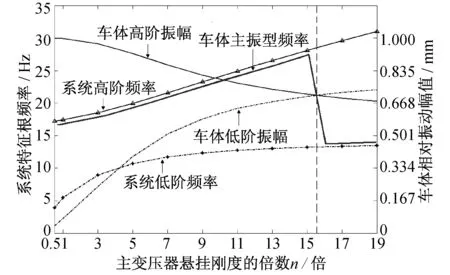
图2 垂向悬挂刚度与车体系统振动频率和车体各阶振幅的关系
从图2中可以看出,车体一阶垂弯频率与主变压器的刚度密切相关,当主变压器垂向悬挂刚度小于16倍原始刚度时,车体的高阶振幅大于低阶振幅,主振型(一阶垂弯)为高阶振动,而当主变压器垂向悬挂刚度大于16倍原始刚度时,车体的低阶振幅大于高阶振幅,主振型为低阶振动,因此车体对应的主振型频率是先为系统高阶频率,后为系统低阶频率。这说明设备悬挂方式对车体频率有非常显著的影响,在结构设计与仿真分析时必须予以重视。
2 悬挂设备对车体频率的影响分析
鉴于车体设备悬挂方式对振动模态的影响,以某轨道交通车辆车体模态有限元分析为例,对车体模态分析过程中悬挂设备的模拟方式及其关键技术进行详细解析。车体模态的有限元分析中,设备的模拟通常有以下四种方法:
(1) 将质量单元直接施加于设备安装位置;
(2) 在设备重心创建一节点,设备质量以集中质量的形式施加在该节点上,然后通过rbe2单元连接在设备安装座上;
(3) 用规则的立方体模拟设备,并用梁单元将其悬挂在设备安装座上;
(4) 用规则的立方体模拟设备,并将其悬挂在设备安装座上,与安装座的连接以设备实际悬挂方式为准,若为弹性连接,则用具有三向刚度的弹簧单元模拟;若为刚性连接,则用梁单元模拟。
图3为车体模态分析的有限元模型中主要的吊挂设备分布。图4为四种模拟方式的模型说明。其中车顶空调、车下变压器和压缩机与车体是弹性连接。表2为四种模拟方式的车体模态分析结果。
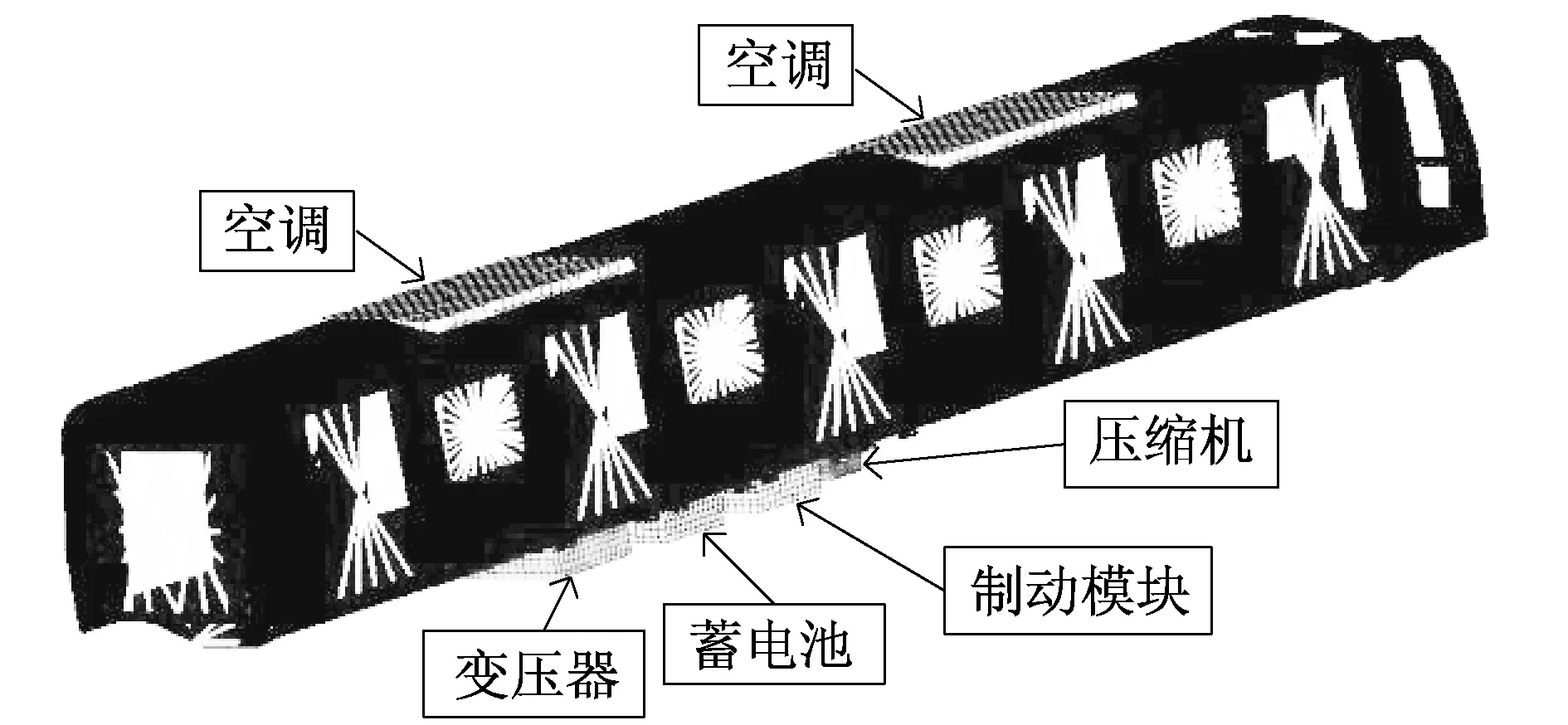
图3 车体主要吊挂设备
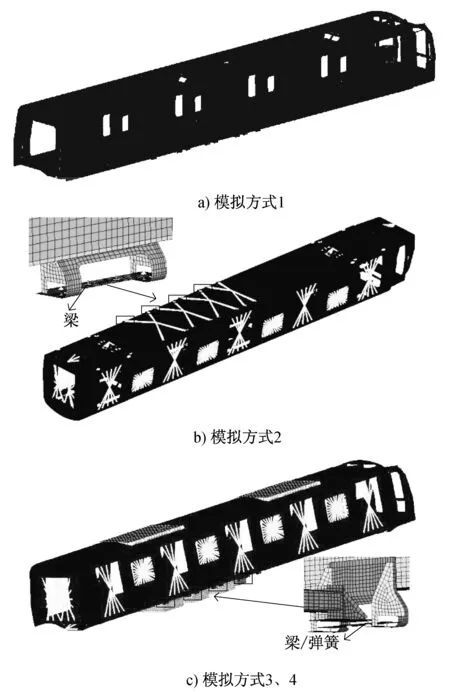
图4 车体模态分析的有限元模型
从表2可以看出,模拟方式1计算得到的各阶频率均小于试验值,模拟方式4计算得到的各阶频率与试验值最接近。这主要是由于,方式1没有考虑悬挂刚度以及设备本身的刚度对车体频率的影响,增加了车体垂直弯曲以及扭转的趋势;方式4相比于方式2和方式3,既考虑了设备本身的刚度,又考虑了悬挂刚度,因此计算结果误差最小。
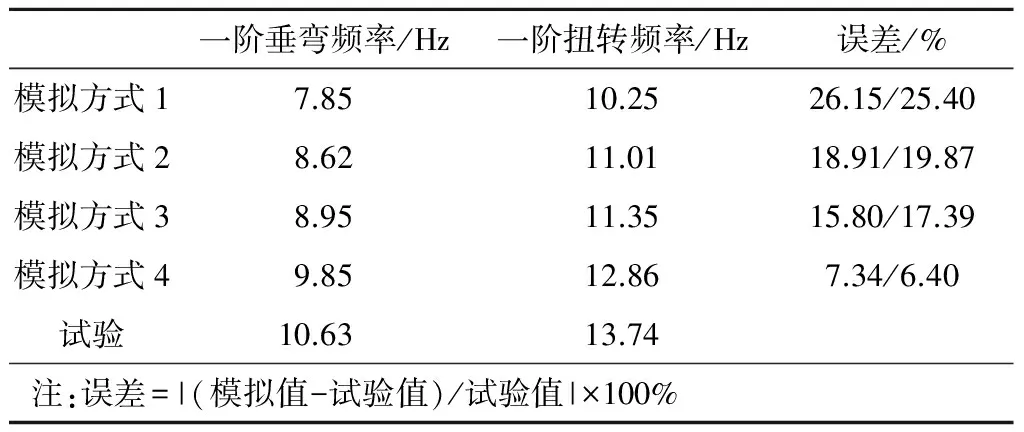
表2 四种模拟方式的车体模态与试验对比
3 内装和设备刚度对车体频率的影响分析
整备车辆在底架下方安装了变压器、逆变器、蓄电池箱等设备,在车顶安装了空调机组,增加了车体的刚性。同时,车体内部装饰对车体刚度的贡献也不容忽视。因此,在对整备车辆车体进行模态分析时,设备、内装的刚度也应予以考虑。
对于吊挂设备,在第2节中提出了用立方体模拟设备的方法,通过与试验的对比分析,证明了其可行性。但车体上大量无法准确模拟的部件(如车体内装、木结构、门窗、行李架等)基本均匀地分布在车内,对车体的整体刚度有一定的影响。采用当量弹性模量法对这些部件进行等效替换。对于铝合金车体,其初始弹性模量(E)为69 GPa,分别将E增加10%和20%,即E为75.9 GPa和82.8 GPa,比较车体主要频率,结果如表3所示。弹性模量与车体一阶垂弯频率和车体一阶扭转频率的关系如图5、6所示。

表3 不同初始弹性模量时的车体主要频率及其变化率
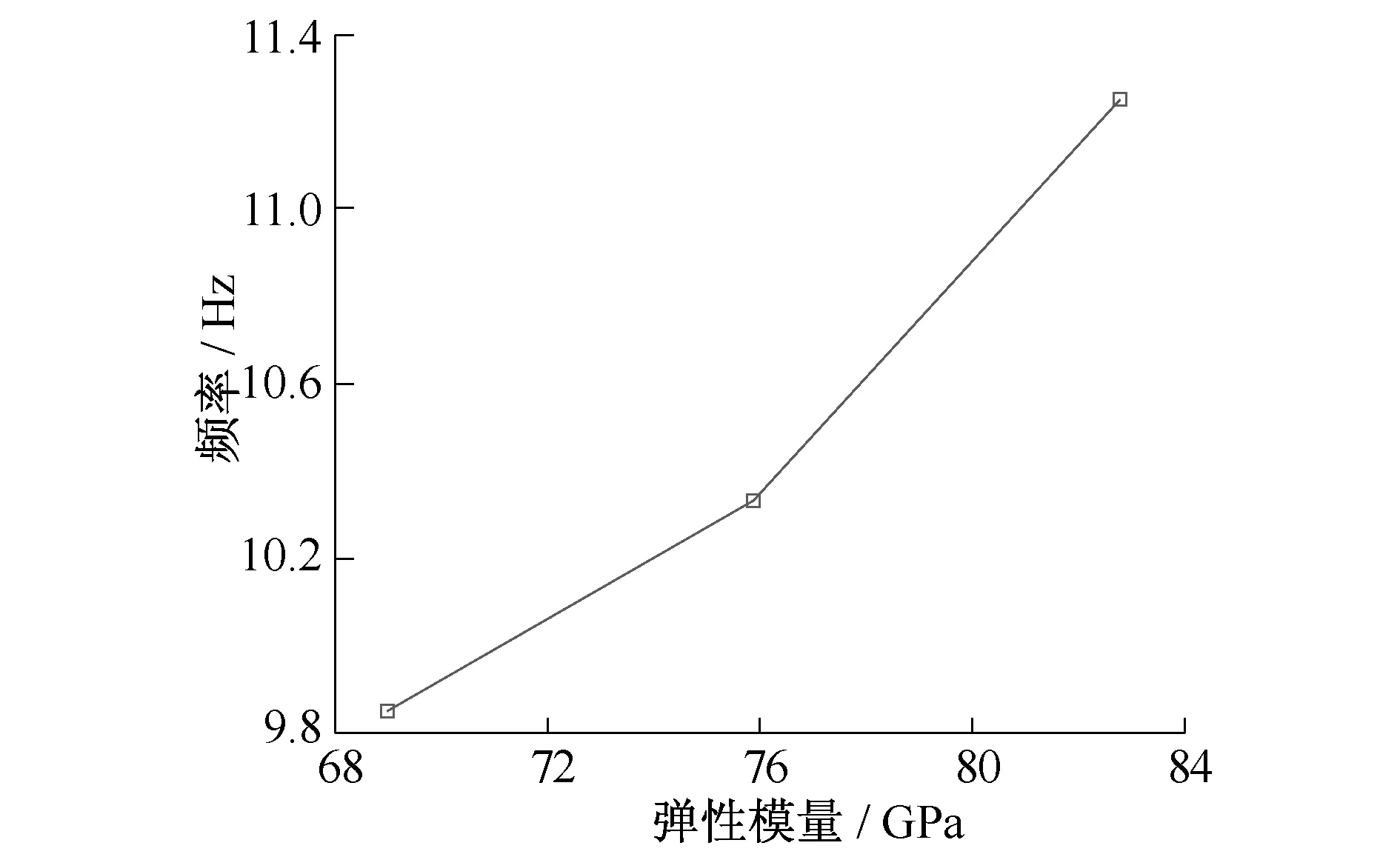
图5 弹性模量与车体一阶垂弯频率变化关系
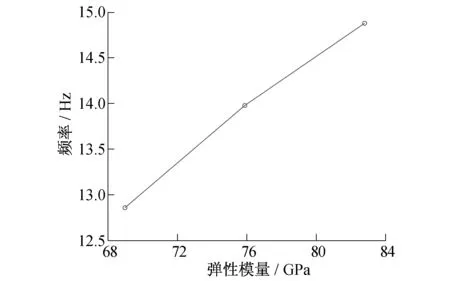
图6 弹性模量与车体一阶扭转频率变化关系
由表3及图5、6可以发现,车体固有频率随着E的增加而准线性增加。在分析过程中,可根据实车试验数据或类似车型的试验数据,利用线性插值的方法修正E值,尽可能地考虑内装刚度对车体固有频率的影响,从而更好地指导车体结构设计。
4 乘客质量对车体频率的影响分析
上、下班高峰期,城市轨道交通车辆内每平米区域高达9人,因此在基于有限元分析的车体结构设计过程中,有必要研究乘客对车体频率的影响。
为进一步研究车体有限元分析中乘客的模拟方法,保证其在车体模态分析时对一阶弯曲固有振动频率不产生影响,又不影响对车体强度的分析以及舒适性评价,在模拟方式4和考虑弹性模量为75.9 GPa的有限元模型基础上,增加了乘客的模拟。将乘客看成1个自由度的弹簧进行模型化,乘客的有限元模型如图7所示。

根据图7中的有限元模型,计算出车体在AW3 (超载)状态下(除座椅区域外,每平米站立9人),车体的一阶垂直弯曲频率为10.25Hz(见图8)。该值与表3中弹性模量75.9GPa的计算值非常接近,说明乘客质量对车体一阶垂弯几乎没有影响,同时也证明了模拟方式的可靠性。
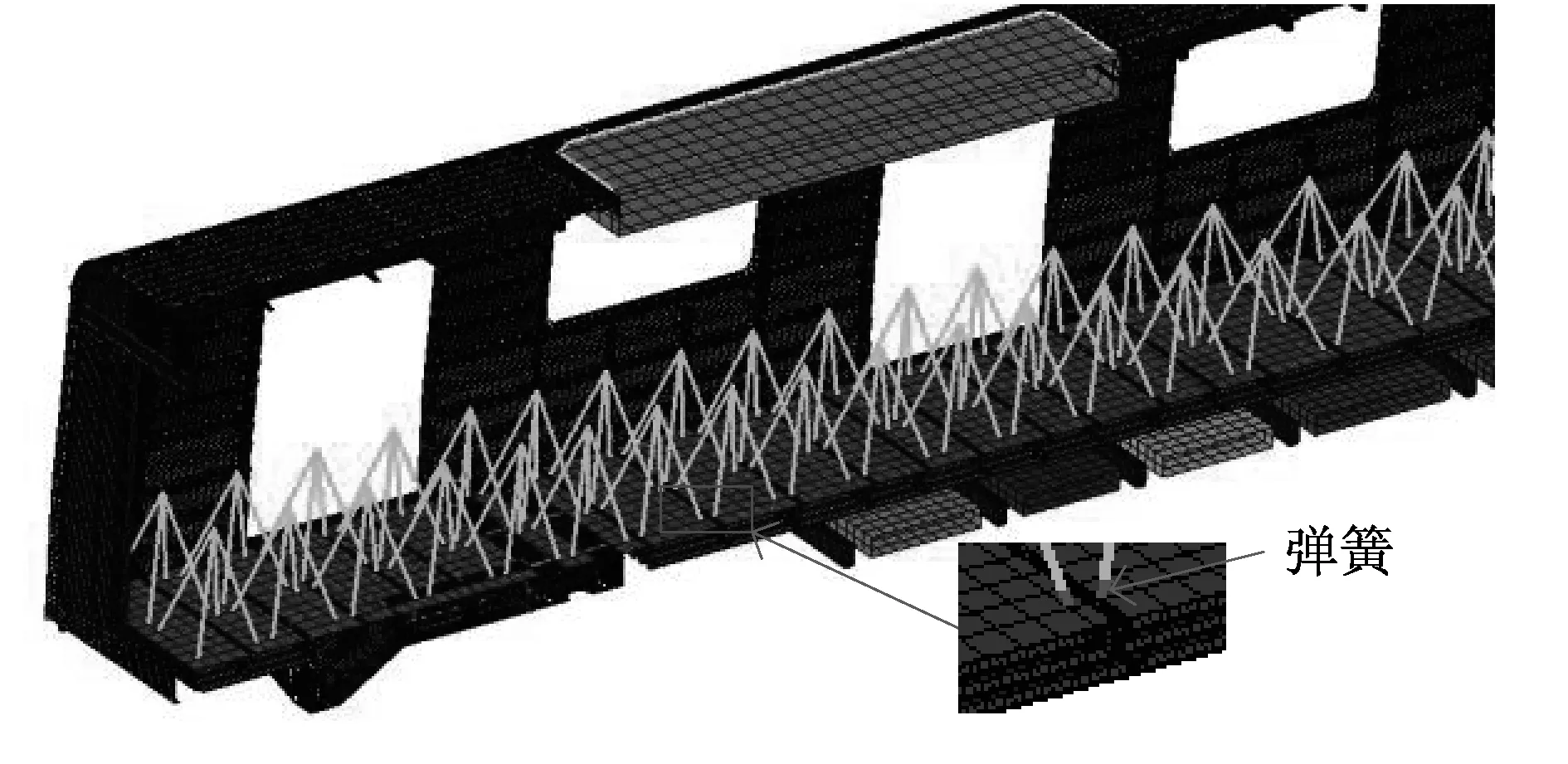
图7 乘客模拟
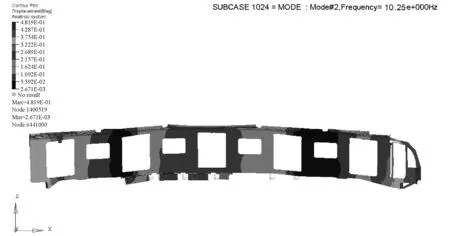
图8 载有乘客的AW3车体一阶垂直弯曲频率
5 结论
本文研究了轨道交通车辆车体模态分析的若干关键问题,得到以下结论:
(1) 设备垂向悬挂刚度的选择与车体系统振动频率和振幅密切相关,是车体结构设计不可忽略的重要因素,应在结构模态分析时予以考虑;
(2) 整备车体模态有限元分析时,设备自身刚度以及悬挂刚度的模拟对车体结构模态有重要影响,应在有限元模型模拟其刚度,并对悬挂刚度进行设置;
(3) 车体一阶垂弯和扭转频率随车体内装及设备自身刚度(有限元分析中,通过改变对应结构的弹性模量来实现)的增加呈线性变化关系,在车体结构刚度评估中应该进行适当等效考虑;
(4) 从研究车体振动模态的角度,乘客对车体一阶垂弯频率几乎没有影响,将乘客看成弹簧进行模型化更接近客观实际,有利于乘客对车体轻量化和振动影响的深入分析。
[1] 周劲松,张伟,孙文静,等.铁道车辆弹性车体动力吸振器减振分析[J].中国铁道科学,2009,30(3):86-90.
[2] 羊玢,孙庆鸿,黄文杰,等.地铁B型车车体静强度及模态计算[J].交通运输工程学报,2006,6(2):1-5.
[3] 郝鲁波,胡青泥,李刚.整备状态下客车模态的有限元分析探讨[J].铁道车辆,2004,42(11):4-7.
[4] 鲁寨军.机车车体模态分析中用质量单元模拟设备重量的方法探讨[J].电力机车与城轨车辆,2003,26 (1):25-27.
[5] 鲁寨军,田红旗,周丹.270 km/h高速动车模态分析[J].中国铁道科学,2005,26 (6):18-23.
[6] 阳光武,肖守讷.弹性悬挂设备对列车整备车体模态的影响分析[J].铁道机车车辆,2012,32(4):37-40.
[7] 吴会超,邬平波,曾京,等.车下设备对车体振动的影响[J].交通运输工程学报,2012,12(5):50-56.
[8] 木村,敏宣.车体振动评估技术的进展[J].国外铁道车辆,2005,42(3):19-23.
Carbody Modal Analysis for Rail Transit Vehicle under Preparation Conditions
ZHAO Shizhong, WANG Jinle, ZHU Tao
The analytic method of vibration frequency and characteristic vector for multi-degree of freedom rigid body system is deduced,and the relationship between equipment suspension style,vertical suspension stiffness,carbody vibration frequency and vibration amplitude are studied.A railway vehicle carbody modal is taken as an example, the influence of the simulation method of equipment suspension,stiffness of car interior and equipment decoration,as well as the passenger weight to the first order vertical bending and torsion frequencies are analyzed in depth, and compared with test result.This research shows that the selection of equipment suspension style and suspension stiffness has significant effect on carbody frequency.By comparing with the test result,and considering of the equipment suspension stiffness,car interior and equipment decoration stiffness,the main vibration modal stiffness of carbody should have obvious improvement during the carbody structure design, while the passenger weight has little impact on carbody main vibration modal frequency.
rail transit vehicle; cabody modal analysis; vibration frequency analysis method; equipment suspension stiffness; car interior decoration stiffness; passenger weight
*国家科技支撑计划项目(2015BAG12B01-15);中央高校基本科研业务费专项资金资助(2682015CX046)
U270.2
10.16037/j.1007-869x.2017.04.007
2015-12-29)

