纵向耦合独立车轮转向架建模方法研究
张 徐 黄运华 王旭嘉 李相欣
(1.西南交通大学机械工程学院,610031,成都; 2.铁道第三勘察设计院集团有限公司,300142,天津//第一作者,硕士研究生)
纵向耦合独立车轮转向架建模方法研究
张 徐1,2黄运华1王旭嘉1李相欣1
(1.西南交通大学机械工程学院,610031,成都; 2.铁道第三勘察设计院集团有限公司,300142,天津//第一作者,硕士研究生)
根据多体系系统动力学理论,在建立动力学模型时,可将车轮间的动力学矢量设计成树形结构,这种处理使车轮间仅生成动力学约束而不是运动学约束。另一种方式将车轮间的纵向耦合方式视为无质量的运动约束,即车轮在连接点处具有相同的运动,运动矢量形成闭环。目前,在建立纵向耦合独立车轮转向架动力学模型时,都采用运动学约束来处理一侧前后车轮的耦合关系。以某COMBINO型纵向耦合独立车轮转向架为例,分别采用运动学约束和动力学约束的方法,对比曲线通过能力,以评价动力学约束方法的合理性。
有轨电车; 纵向耦合; 独立车轮转向架; 运动学约束; 动力学约束
First-author′s address School of Mechanical Engineering, Southwest Jiaotong University,610031,Chengdu,China
在进行车辆系统动力学分析时,首要的一步是利用多体系统动力学软件建立车辆动力学模型。建模过程中,复杂环节的处理对动力学计算结果的影响至关重要。不同的约束方式对模型的仿真结果可能会有影响,也可能没有影响,究竟采用何种方式,一直是困扰设计者们的一个难题。
本文以某COMBINO型纵向耦合独立车轮转向架为例,分别采用运动学约束和动力学约束[1]进行建模、仿真对比,从而说明动力学约束是否适用于建立转向架的纵向耦合模型。
1 动力学计算模型
本文的研究对象是某四模块低地板有轨电车(见图1)。四模块分别为Mc2(动车)、M(动车)、T(拖车)、Mc1(动车)。4个转向架中有3个独立旋转车轮动力转向架(纵向耦合)和1个独立旋转车轮拖车转向架。此有轨电车不同于传统车辆,需以整列编组作为动力学分析对象,并采用SIMPACK动力学仿真软件进行仿真试验。

图1 四模块低地板有轨电车模型
2 纵向耦合独立车轮转向架简介
相对于传统轮对,独立车轮转向架[2]缺乏由纵向蠕滑力而产生的导向力矩,故在曲线上无自导向功能,基本只能靠轮缘导向。对于纵向耦合独立车轮转向架[3](见图2),电机均速驱动一侧的车轮,当滚动圆半径不一致产生速度差时,前后车轮产生纵向蠕滑力。蠕滑力作为曲线通过性能的重要指标之一,是车辆动力学研究领域中的重要课题,需对其进行推导说明。转向架基本参数见表1。

图2 纵向耦合独立车轮转向架模型
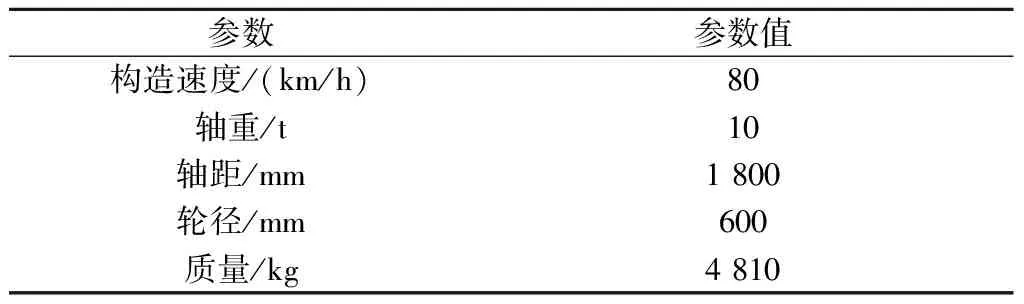
表1 转向架基本参数
3 纵向耦合独立车轮转向架蠕滑力公式推导
在轮对大横向位移和大冲角的情况下,要考虑车轮超前和滞后角的影响。由于推导计算公式的过程中假设轮对位移和冲角较小,故可忽略车轮超前和滞后角的影响。
根据多体系统动力学的知识[4],建立轨道固定惯性坐标系xyz;绕z轴旋转ψ,得中间坐标系x′y′z′;绕x′轴旋转φ,得轴桥连体坐标系x″y″z″;绕y″轴旋转γL,得左侧车轮连体坐标系xLyLzL,绕y″轴旋转γR,得右侧车轮连体坐标系xRyRzR。
设左侧车轮和右侧车轮的旋转角速度分别为ΩL、ΩR。左侧接触圆中心点距轴桥连体坐标系x″y″z″处的距离为lL,右侧接触圆中心点距轴桥连体坐标系x″y″z″处的距离为lR。左侧接触圆半径为RL,右侧接触圆半径为RR。轮轨接触角分别为δL,δR。纵向蠕滑系数和横向蠕滑系数分别为f11、f22。
各坐标系之间的转换关系为:
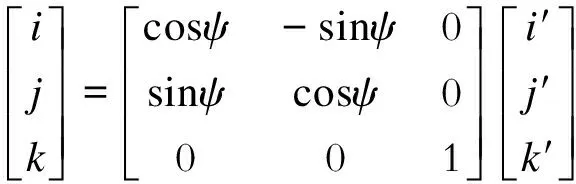
(1)
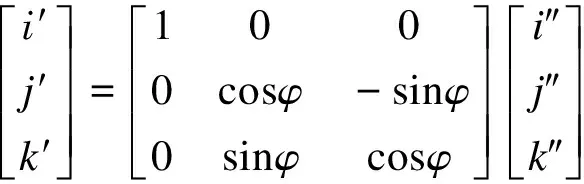
(2)
根据式(1)、(2)得:
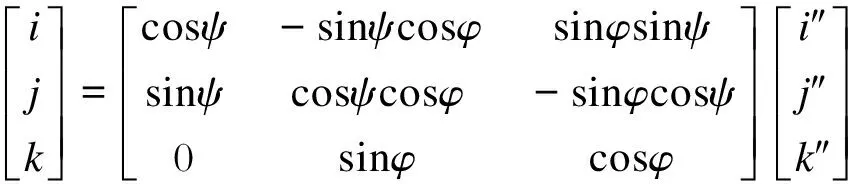
(3)
轴桥连体坐标系x″y″z″相对于轨道固定惯性坐标系xyz的角速度为:
(4)
左、右轮连体坐标系xLyLzL、xRyRzR相对于轨道固定惯性坐标系xyz的角速度为:
(5)
左、右侧接触圆中心点处的速度为:
(6)
由于不考虑超前和滞后角,得:
RL,R=-RL,Rk″
(7)
左、右侧轮轨接触点处的相对速度为:
vwheelrailL,R=vaxleL,R+ωL,R×RL,R=
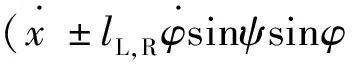
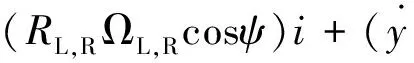
(8)
轮轨接触点处接触斑坐标系eL、eR与轴桥连体坐标系x″y″z″的关系如下:
(9)
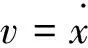
(10)
左右接触斑处的纵向蠕滑率和横向蠕滑率为:
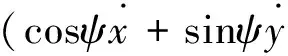
(11)
根据Kaller线性理论可知,纵向蠕滑力与横向蠕滑力分别为:
FxL,R=-f11ξxL,R=
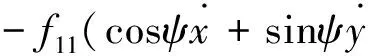
FyL,R=-f22ξyL,R=
(12)
对比文献[5]中的公式,本文推导的蠕滑力公式与之基本一致。因此,本文的推导结果是可信的,也是可以采用的。
4 曲线通过性能对比
动力学约束方法的具体操作如下:力元作为物体间的联系仅限于力的作用而不附加任何动力学上的约束。由于纵向耦合独立车轮转向架中同侧车轮的角速度相等,且由同一个电机控制,故采用SIMPACK软件中14号力元Gearbox Torque to Torque。此力元的作用就是提供齿轮之间的弹性传动,并在两齿轮上传递相互作用力,考虑到车轮角速度相等,通过等效直接将传动比设置为1∶1。
此转向架通过曲线时,导向力主要由纵向蠕滑力[6]提供。通过分析可知,当采用动力学约束方法时,纵向蠕滑力的大小和约束力元的大小有关。分别将力元刚度设置为103Nm/rad、105Nm/rad和107Nm/rad,并与采用运动学约束建模的进行比较。
由于本文采用的低地板有轨电车有3个纵向耦合独立旋转车轮转向架,且参数一致,故仅对Mc1车下的转向架进行分析。仿真时线路采用城轨车辆常用的S型曲线轨道,具体参数见表2。不考虑轨道的随机不平顺,且有轨电车在惰行的情况下通过曲线,对比纵向耦合独立车轮转向架一、二位轮对的导向能力。

表2 S型曲线参数
4.1 纵向蠕滑力和约束力矩
将采用运动学约束的模型称为工况一,刚度为103Nm/rad的动力学约束称为工况二,刚度为105Nm/rad的动力学约束称为工况三,刚度为107Nm/rad的动力学约束称为工况四。
根据图3~6,当有轨电车运行在S型轨道上的驶进直线段时,不论是何工况,由于前后车轮速度相等,速度差值为0,不会产生纵向蠕滑力;当转向架驶进圆曲线中时,由于转向架采用的是纵向耦合方式进行耦合,一侧车轮的角速度基本一致,但前后车轮滚动圆半径不一致,从而使同侧前后车轮之间产生速度差,形成转向架通过曲线时所需的纵向蠕滑力;当转向架驶进中间夹直线时,由于夹直线的长度远小于车辆的长度,前后车辆会处于不同的曲线段,从而产生速度差,导致产生纵向蠕滑力;而当转向架进入下一段圆曲线时,由于与前一段圆曲线半径大小相等,长度基本一致,仅仅是半径方向不同,故纵向蠕滑力的变化趋势相反;最后,当转向架完全驶出曲线进入直线段时,纵向蠕滑力会逐渐趋于0。
此外,从图3~6中可看出,工况二、工况三中力元刚度较小,对前后车轮约束不充分,产生不了足够的纵向蠕滑力来形成曲线导向力矩,只有工况四中的纵向蠕滑力与工况一中纵向蠕滑力的变化情况一致。另外,转向架同侧前后车轮之间的纵向蠕滑力大小相同,方向相反,符合纵向耦合转向架的特点,且随着约束力元越来越大,特征越来越明显。
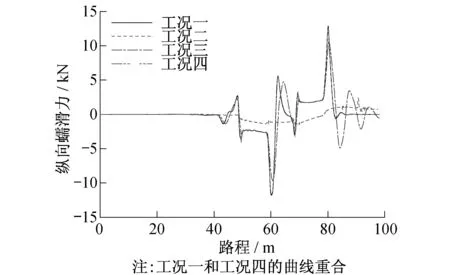
图3 一位轮对右轮纵向蠕滑力
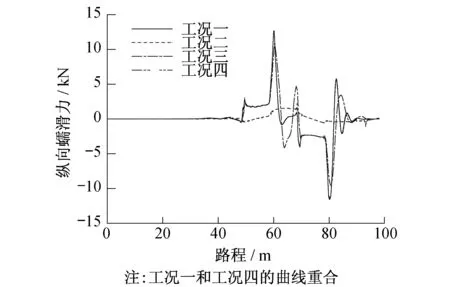
图4 一位轮对左轮纵向蠕滑力
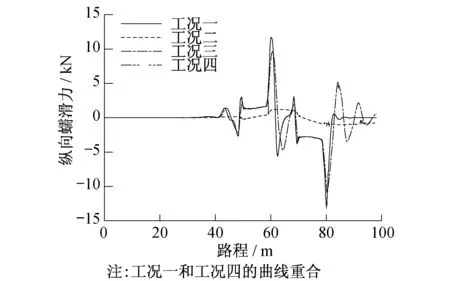
图5 二位轮对右轮纵向蠕滑力
对比左右电机约束力矩,以工况一的实际情况对比其余三种工况发现:工况二基本不产生约束力矩;随着力元刚度逐渐变大,工况三和工况四中的约束力矩越来越接近工况一的情况;工况四和工况一中的约束力矩情况相同。如图7、8所示。
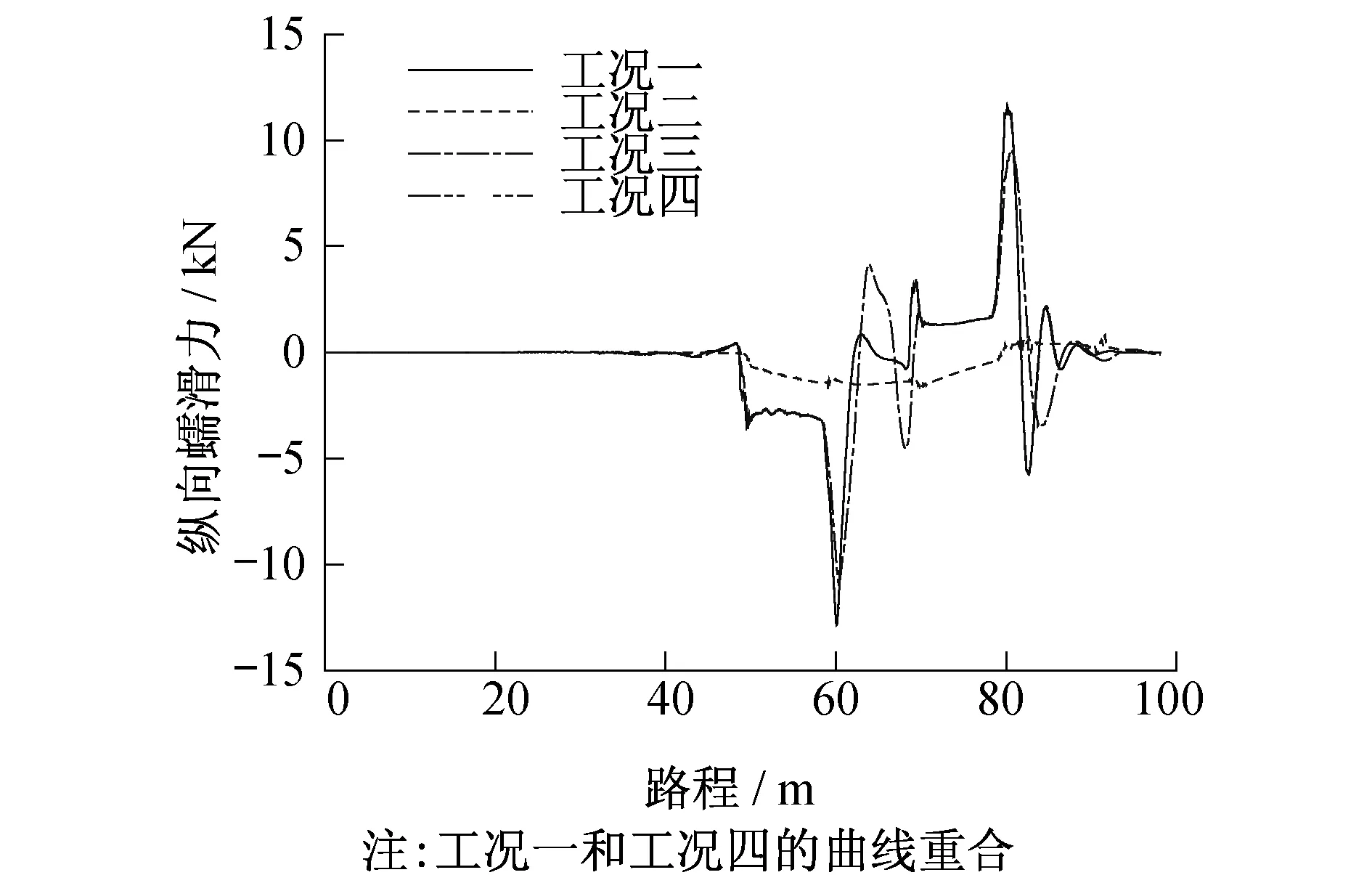
图6 二位轮对左轮纵向蠕滑力

图7 左侧电机约束力矩
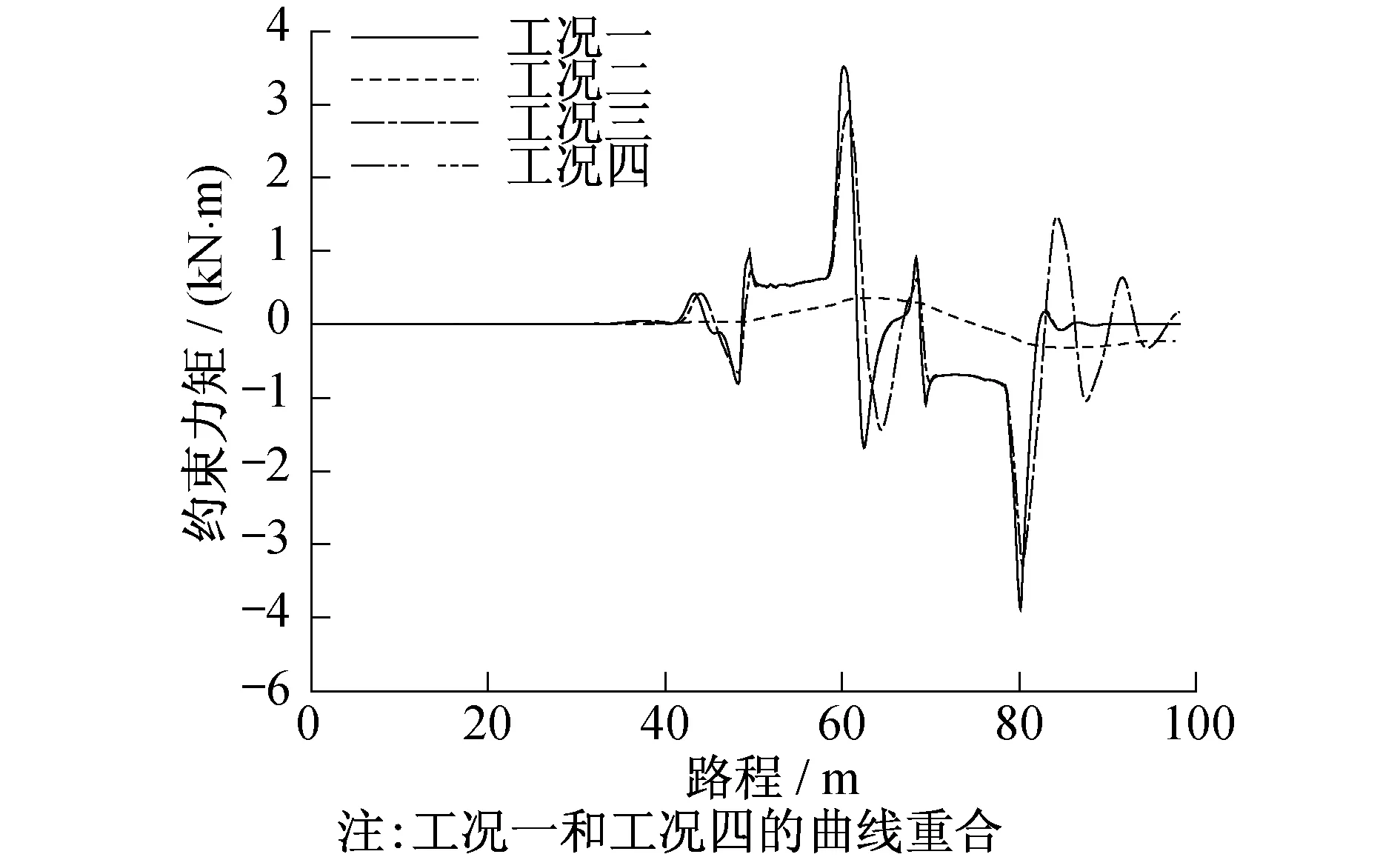
图8 右侧电机约束力矩
4.2 曲线通过指标
除了纵向蠕滑力和电机约束力矩外,运动过程中轮组的横移量[7]也是评价转向架对中能力的指标之一。仿真中发现,工况二在S型曲线轨道中运行时轮组横移量波动最大,而工况三在夹直线段处出现最大横向位移量(均是由于力元刚度不合适引起的);工况四与工况一一致,最大值出现在曲线段,通过夹直线时横向位移量变化较小,且进入直线轨道后都在向0点缓慢靠近(当增加直线轨道长度,横移量能归0)。如图9、10所示。
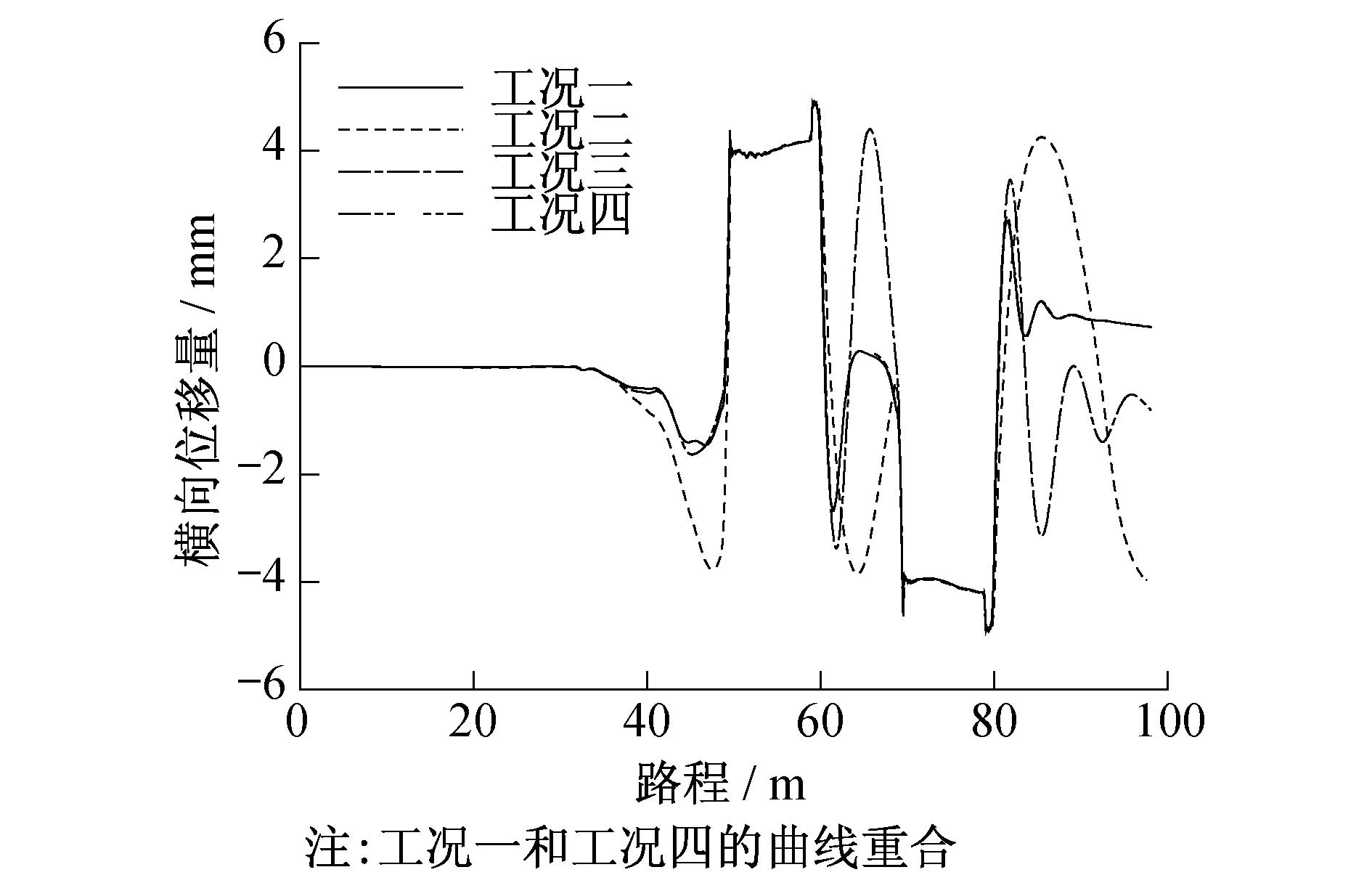
图9 一位轮对横移量
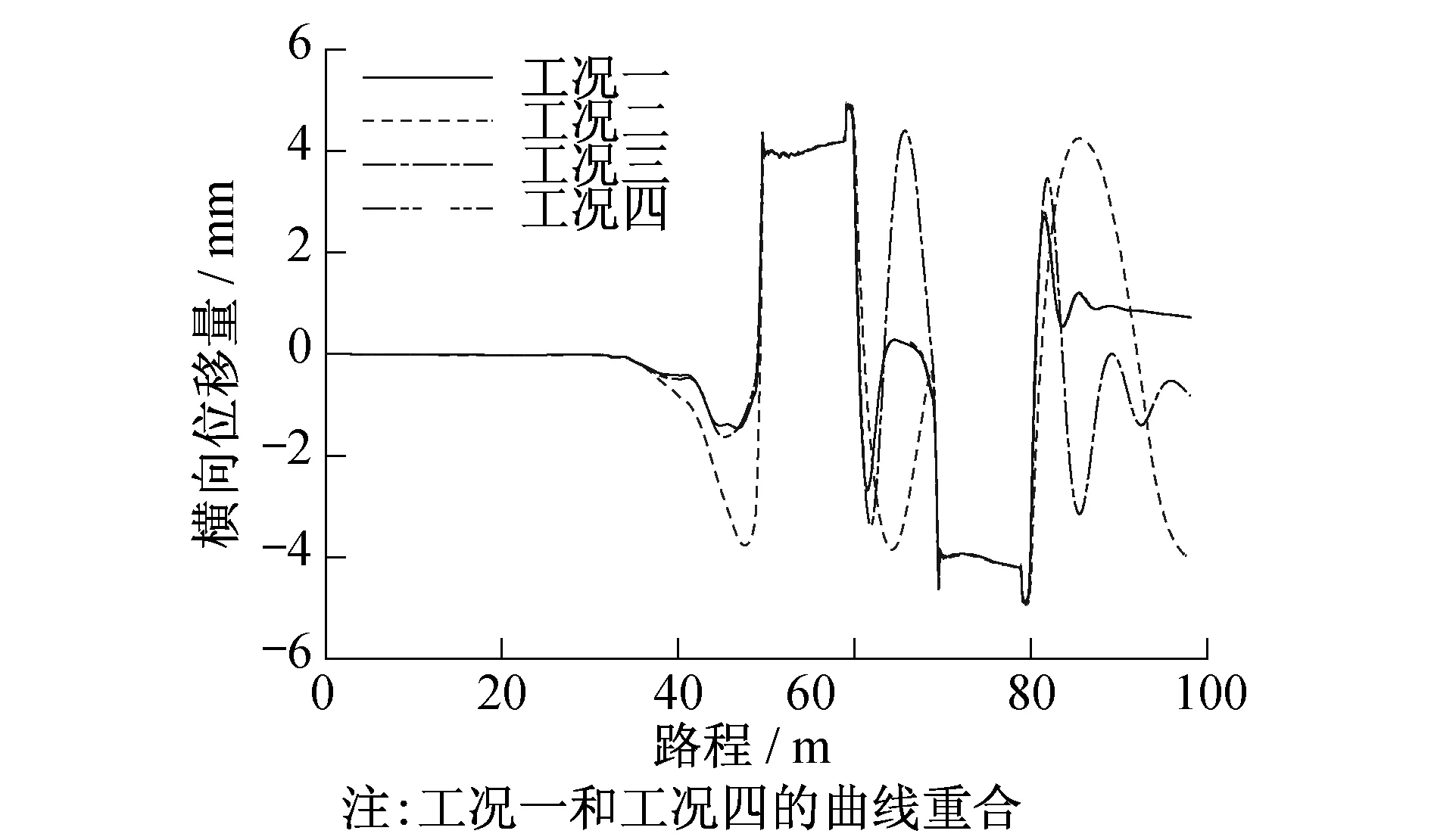
图10 二位轮对横移量
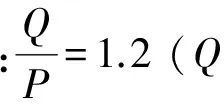
此指标适用于低速脱轨情况,脱轨系数不超过危险限度是安全的,不超过允许限度是希望达到的。对于设计的车辆来说,希望不超过允许限度。
从图11~14中可看出,在刚刚驶进曲线段中时,各工况脱轨系数变化基本一致,当转向架驶出曲线段进入直线段后,工况二下的脱轨系数会产生波动,而其余工况下均会稳定于固定值。工况三下,一位轮对的左轮和二位轮对的右轮在进入圆曲线轨道时,脱轨系数会突然增大,其原因主要由于此处曲线半径小,且没有过渡曲线,纵向蠕滑力也小,导致通过曲线时冲角较大,通过曲线的能力降低。同样的情况出现在进入、驶出直线轨道处一位轮对的左右轮。只有工况四和工况一基本一致,且未超过允许限度。
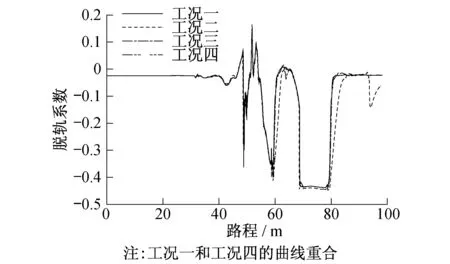
图11 一位轮对左轮脱轨系数
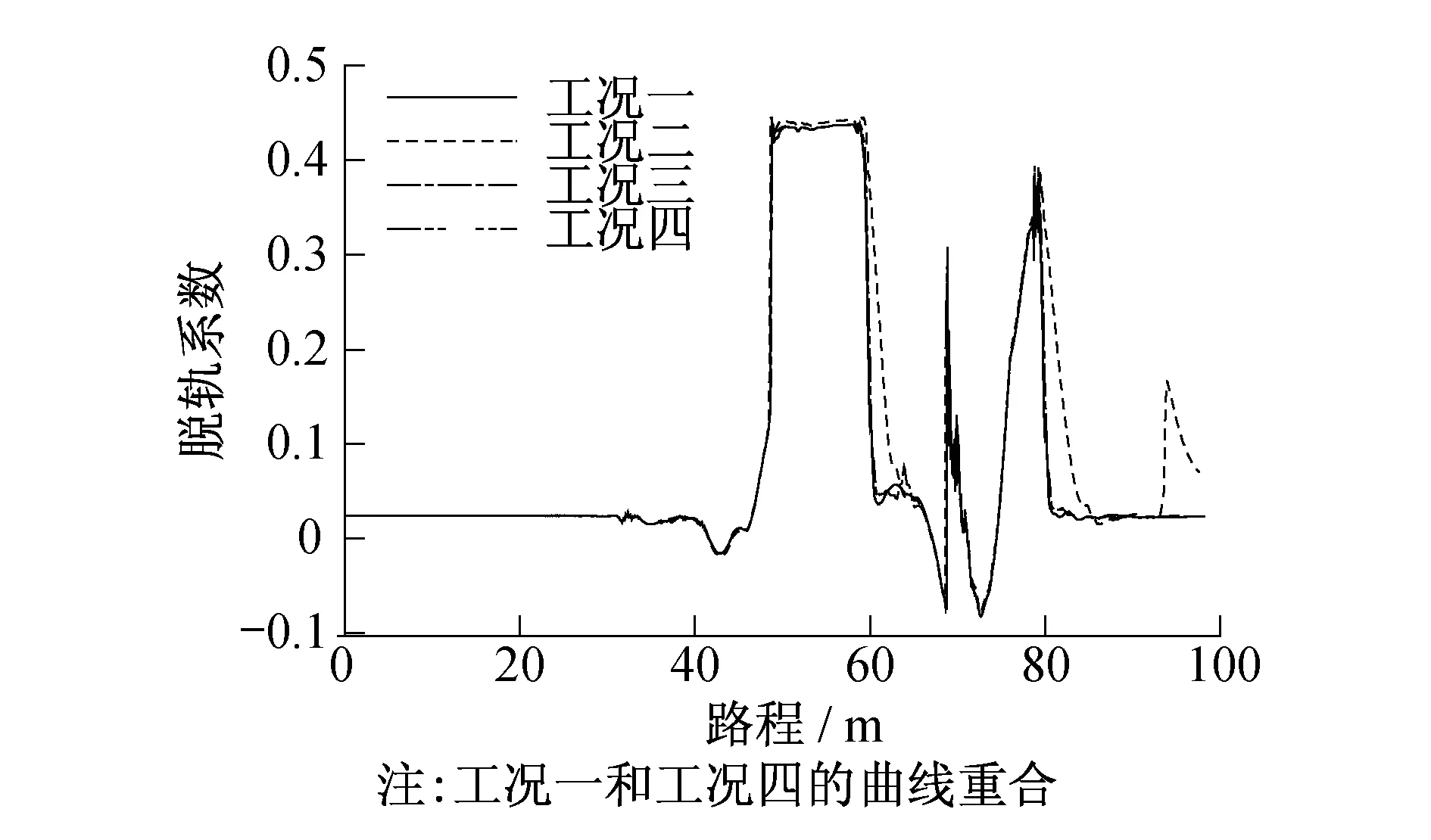
图12 一位轮对右轮脱轨系数
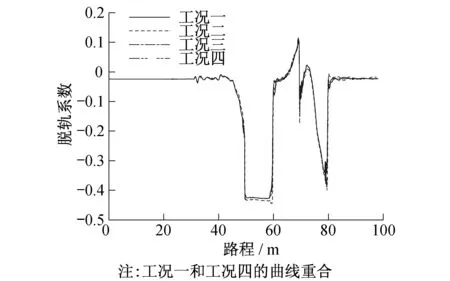
图13 二位轮对左轮脱轨系数
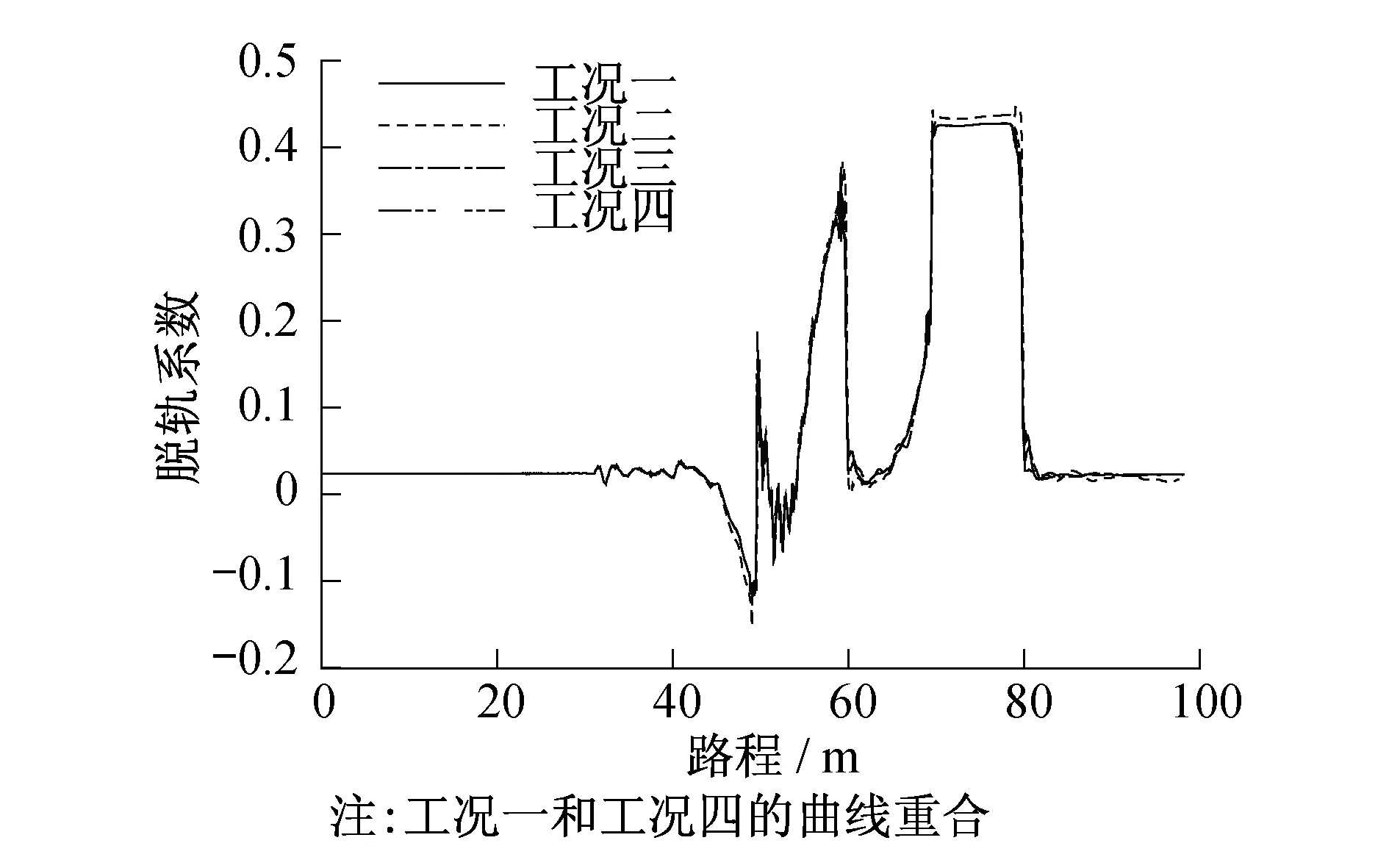
图14 二位轮对右轮脱轨系数
5 结语
对纵向耦合独立旋转车轮转向架分别采用运动学约束和动力学约束进行建模比较发现,树结构的多体系统模型同样适用于建立此转向架的仿真模型。但通过选取不同刚度的力元,发现刚度的选取对转向架模型的影响很大,刚度选取较小,转向架一侧的前后车轮约束不够,产生的纵向蠕滑力较小,不能提供转向架的导向力;而刚度选取过大,前后车轮产生的约束力会变大,导致车辆曲线通过性能不稳定,甚至不能完整通过曲线。比较发现,当刚度为107Nm/rad时,采用动力学约束的模型获得的动力学性能最大限度接近闭合环系统的模型。
需要指出的是,本次研究仅限于转向架耦合方式下两种建模方法的比较,发现两种方法均可。此外,采用哪种方法建立车体间连接件也是模型建立中需要重视的地方,需在以后的模型建立中进行分析。
[1] 罗世辉.大连低地板有轨电车的动力学性能[J].机车电传动,2001(3):28-31.
[2] Frederich F.A bogie concept for the 1990s[J].Railway Gazette international,1988(9):583-585.
[3] 许明春,曾京.纵向耦合独立车轮转向架导向机理[J].交通运输工程学报,2011,11(1):43-50.
[4] 洪嘉振.计算多体系统动力学[M].北京:高等教育出版社,1999.
[5] 金雪松,刘启跃.轮轨摩擦学[M].北京:中国铁道出版社,2004.
[6] 任毅,李芾,黄运华.独立旋转车轮动力学性能研究[J].铁道机车车辆,2008,28(6):15-19.
[7] 李石平,刘启灵.独立旋转车轮打磨小车曲线通过分析[J].机车电传动,2014(5):15-16.
[8] 王福天.车辆动力学[M].北京:中国铁道出版社,1981.
On Longitudinal Coupling Modeling of Independent Wheel Bogie
ZHANG Xu, HUANG Yunhua, WANG Xujia, LI Xiangxin
According to the multi-system dynamics theory,in building a dynamic model,the dynamic vector between wheels could be designed into a tree structure,which generates only dynamic constraint rather than kinematic constraint. Another way of modeling the longitudinal coupling between wheels is a massless motion constraint,namely the wheels in connection with the same motion, and the motion vector forms a closed loop.At this stage,in building the longitudinal coupling bogie with independent rotating wheels,kinematics constraint is used to deal with the side wheels.In this paper,according to a COMBINO longitudinal coupling independent wheel bogie, the dynamic constraint is used and the rationality of the dynamic constraint method is expounded through a comparison with the curve passing capacity of the kinematics constraint method.
tram; longitudinal coupling; independent wheel bogie; kinematic constraint; dynamic constraint
U270.331
10.16037/j.1007-869x.2017.04.006
2015-05-28)

