立足“基本图形” 突破数学“题型”

陶明

（浙江省台州市白云学校）

立足“基本图形” 突破数学“题型”

陶明

（浙江省台州市白云学校）

初中数学几何教学重在“题型”的归纳与总结，通过对中考试题的剖析，提取其背后的几何“基本图形”，以及题型组织形式，从而归纳出该类“题型”，再对实际数学解题中的“类似”题目对比探究，进一步总结该题型及其解法．

基本图形；数学题型；中考试题

我们都知道，精细化的学习关键在于知识的整理、分类.而之于数学，“题型”是其中一种重要的分类方法，面对浩瀚无边的数学题海，“题型”分类就显得格外重要.而在实际学习中，很多学生面对一些综合性较强的几何题目却无从下手，那么，为什么平时已经“千锤百炼”，关键时刻还是“望题兴叹”呢？很大一部分原因在于他们不会总结归纳题型.

一、例题剖析，完整解答

如何掌握几何综合题的题型呢？下面以一道中考试题为例，对“几何题型”进行归纳分析.

例1（2014年山东·淄博卷）如图1，在直角坐标系中，点A的坐标是A（0，3），点C是x轴上的一个动点，点C在x轴上移动时，始终保持△ACP是等边三角形.当点C移动到点O时，得到等边△AOB（此时点P与点B重合）.

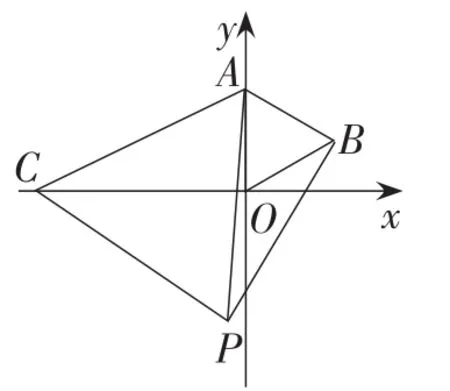
图1

（1）点C在移动的过程中，当等边△ACP的顶点P在第三象限时（如图1），求证：△AOC≌△ABP.由此你发现什么结论？

（2）求点C在x轴上移动时，点P所在函数图象的解析式.

这是一道中等难度的几何题，解决此题的关键在于剖析其背后隐含的“考点”.仔细分析，此题主要考查了初中几何的两个重要“基本图形”.

基本图形1

如图2，等腰△ABC和等腰△ADE（AB=AC，AD=AE）绕顶点A旋转，若两顶角相等（既两个等腰三角形相似），则△ABD≌△ACE.进一步特殊化，当这两个三角形分别是等边三角形或等腰直角三角形时，结论自然也满足.

图2

基本图形2

等腰三角形底边上的两顶点若有一点在一条直线上运动，那么另一点的运动轨迹也是一条直线.如图3，在等腰△ADE中，固定顶角顶点A，底边上一顶点D在直线m上运动，则点E的运动轨迹也是一条直线（直线n）.

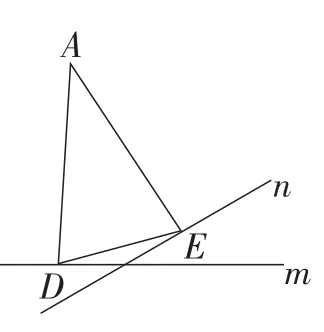
图3

其实，在近些年中考几何题中，只要我们细心斟酌、仔细分类，以“基本图形”为载体的“知识点”大有题在.

题1（2012年吉林卷）如图4，在等边△ABC中，D是边AC上的一点，连接BD，将△BCD绕点B逆时针旋转60°，得到△BAE，连接ED，若BC=10，BD=9，则△AED的周长是_______．

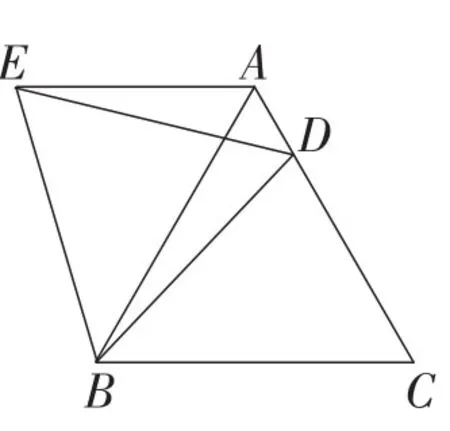
图4

此题只要在△BCD≌△BAE的基础上再探究，答案为19．

题2 （2015年山东·日照卷）如图5，已知，在△ABC中，CA=CB，∠ACB=90°，E，F分别是CA，CB边的三等分点，将△ECF绕点C逆时针旋转角α（0°＜α＜90°），得到△MCN，连接AM，BN.

图5

（1）求证：AM=BN；

（2）当MA∥CN时，试求旋转角α的余弦值.

此题只要发现△CBN≌△CAM，就比较容易证明（1）的结论，也可得出α的余弦值为

以上两例都是“基本图形1”的应用，两题都是在利用基本图形1得到基本结论的基础上再进行细致探究而进行解题，其解题思路如出一辙.事实上，如果将“基本图形1（如图2）”中的两个等腰三角形换成两个相似且同向的△ABC和△ADE，类似找到的两个△ABD和△ACE也相似（此结论在初中阶段更有其一般性，应用很广）.

题3（2015年山东·威海卷）（1）如图7（1），已知∠ACB=∠DCE=90°，AC=BC=6，CD=CE，AE=3，∠CAE=45°，求AD的长.

图6

（2）如图7（2），已知∠ACB=∠DCE=90°，∠ABC=∠CED=∠CAE=30°，AC=3，AE=8，求AD的长.

第（1）小题中只要得出△CAD≌△CBE就易得AD=BE=9.而第（2）小题是要通过△CAD∽△CBE得到AD=

由此可见，以“基本图形1”为基础进行知识点归纳可以很明确地看出该类题的考查知识点和方法技能，可以触类旁通地想出该题的解题思路和结果，显然，“基本图形2”所考查的也是一类知识点（这里不再展开，读者可以在下文“一题多变”中发现类似结论）.而篇头例题正是将两个基本图形合理组合、组织合成.通过对两个基本图形的深入探究，进而我们可以得出该例题解答如下.

（1）证明：因为△AOB与△ACP都是等边三角形，固由“基本图形1”，得△AOC≌△ABP（SAS）.所以∠COA=∠PBA=90°，所以点P在过点B且与AB垂直的直线上或PB⊥AB或∠ABP=90°.

（2）点P在过点B且与AB垂直的直线上（结合第（1）小题和基本图形2得到，接下来只要用待定系数法求出该直线）.易得B，当点C移动到点P在 y轴上时，得P（0，-3）.所以点P所在直线解析式为y=

二、题型归纳，通法提炼

对于一道综合性较强的几何题，我们对它的反思决不能止于“就题论题”，而要继续刨根问底，深入探究其考点所组合的“题型”.事实上，数学“题型”是由几个考点按照一定组织形式组合而成，而例题背后的“题型”是由两个“基本图形”按照其“组织形式”所生成，故该题型分解如下.

（1）基本图形（图2和图3对应的考点）；

（2）组织形式.

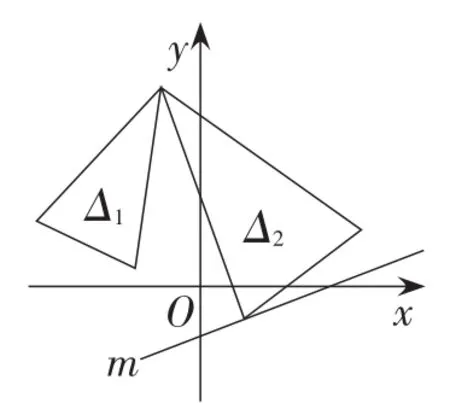
图7

题型：如图7，在平面直角坐标系中，已知一等腰三角形 Δ1（即其相关的量已知且不变），与之有共同顶角顶点且相似的等腰三角形Δ2中底边一顶点在直线m上运动，则其底边另一顶点是不是也在一条直线上运动？如果是，求出该直线n并说明理由.

通过如上探析，我们可以发现该类题型的解答关键在于对“基本图形”的剖析，所以“基本图形”是该题型的核心，而“组织形式”只是将“基本图形”相互贯通、有机融合的框架.由上可见该题型一般有两个待解问题：“直线n的求法”，以及“证明点E轨迹就是此直线”，即证明基本图形2的结论，以下给出其中一种解题方法.

（1）直线n的求法：两次移动点D，利用基本图形1中两个三角形的全等关系，通过对应边和对应角的转化，求出两个特殊点E，继而用待定系数法求出该直线.

（2）证明点E的轨迹是直线n：将动点D的坐标用字母来表示，通过计算，求出此时点E用该字母表示的坐标，证明点E满足直线n（详见下文中题1的解法）.

显然，例题中等边△ABO和等边△ACP即为Δ1和Δ2，x轴为直线m，最后点P所在的直线即为直线n，其中例题只要求出直线n.

为方便计算，该题型具体题目中Δ1和Δ2一般都是特殊的等腰三角形，如等边或等腰直角三角形（正方形可转化成等腰直角三角形），因为Δ1中各个量皆已知，所以其解题过程即是通过基本图形1的转化求出并证明基本图形2的结论.

三、一“题”多变，多变归一

我们通常在大量的解题中，经常会发现与该例题“相似”的题目，如果我们再仔细解剖，往往会发现这些题目的本质万变不离其宗，而这“宗”正是该题型（包括该题型解法）.

题1 如图8，在正△AOB中，A（2，0），C是x轴上一个动点△BCD也是正三角形.

（1）求点B的坐标；

（2）当点C分别落在几个特殊点时，求出相应的点D的坐标（填写表1），并判断这些点是否在同一直线上；

图8

（3）当点C运动时，点D一定在一条固定的直线上运动吗？若是，求出这条直线的解析式；若不是，说明理由.

表1

显然，第（1）小题与该题型中的各要素完全吻合，以下给出其简要解题过程（相较于例题的解法，此题解法给出了证明点D轨迹就是直线n的证法）.

简单答题如下：如图9，连接AD，过点D作DH垂直x轴于点H.

图9

（3）设点C的坐标为C(a ，0)，由△OBC≌△ABD，可得∠BAD=∠BOC=60°.由∠BAO=60°，得∠DAH=60°，且AD=OC=|a|.故得故.显然点D满足

此题给出了点D运动轨迹在同一直线上的证明.

题2 如图10，在平面直角坐标系中，四边形OABC是正方形，点A，C分别在x轴，y轴上，且A（2，0），在线段AB上一个动点D，连接CD，过点C作CE垂直于CD交x轴于点E，以CE，CD为邻边作矩形CEFD.

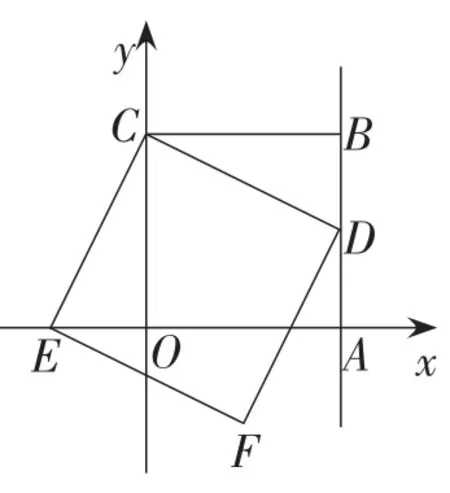
图10

（1）求证：矩形CEFD是正方形；

（2）若点D的纵坐标为1，直接写出点E，F的坐标；

（3）若设点D的纵坐标为a，求点F的坐标（结果用含a的代数式表示）；随着点D的移动，点F是否始终在一条直线上？如果是，求出这条直线的函数解析式；如果不是，说明理由.

此题是两个正方形绕点C旋转，但进而分析，此题无非就是该题型的变式之一，实际上看成Δ1和Δ2（即△ECD和△OCB）都是两个等腰直角三角形，其余证法类似（第（3）小题只要设点D的坐标为D（2，a），再求出点F的坐标满足直线即可.

题3 在平面直角坐标系中，如图11（1），在正方形OABC中，点B（2，2），A，C分别是x轴、y轴正半轴上的点，P是直线y=-x上的动点，作BM⊥BP，且保持∠BPM=45°.

（1）如图11（2），若点P（0，0），此时，点M的坐标是________；

如图11（3），若点P（2，-2），此时，点M的坐标是________.

（2）根据（1）中的观察和计算，试猜想一般情况下点M的纵坐标y和横坐标x之间有什么关系？如果还是想不出来，可以再画出特殊情形观察，你的猜想是__________（y与x之间的关系式）；如果点M在第一象限，如图11（4），你能证明自己的猜想吗？试一试！

图11

此题中Δ1和Δ2分别是△ABC和△PBM，直线m为y=-x，求法同上.

通过如上3道题的比较探究，不难发现它们都是同种题型的不同题目表达，而其解题过程和方法如出一辙.数学解题能力中的重要一环是让复杂问题简单化，而对以上几道题的题型归纳正是此种能力的有效思维方式.

四、归纳分析，总结方法

类似于如上提到的两个基本图形，初中数学中还有许多比较常用的基本图形.

如图12，直线AB∥CD，FG平分∠EFD，则有△GEF是等腰三角形（角平分线+平行线）；

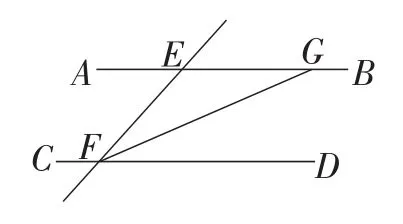
图12

图13

如图13，△BAC为等腰直角三角形，AB=AC，直线m过点A，且BD，CE分别垂直直线m于点D，E，则有△ABD≌△CAE（一线三直角）；

如图14，经过平行四边形中点的线段互相平分，且把平行四边形的面积分成相等的两部分（重心等分面积）.

图14

……

几何学习的难点在于其定理选取运用的灵活性，而每个基本图形都可以看做相关定理的基本组合运用，事实上，数学几何里的很多“题型”都是由一个或多个“基本图形”组成，所以我们在教数学知识的时候，既要让学生掌握最基本的概念或定理，又要掌握数学基本图形，正是它们的相互组合才让数学几何题型这么“丰富多彩”.

［1］朱桂平.提取模型、融会贯通［J］.中国数学教育（初中版），2014（7/8）：101-103.

［2］陈德前.模型“烹大餐”教学得启示［J］.中学数学教学参考（中旬），2013（7）：48-49.

2017—02—13

陶明（1985—），男，中学二级教师，主要从事有效教学、有效课堂研究.