一次区域教研说题比赛及体会

于 彬，高振卿

（山东省东营市胜利第六中学）

一次区域教研说题比赛及体会

于 彬，高振卿

（山东省东营市胜利第六中学）

说题是一种新兴的教研形式，深受教研部门和一线教师喜欢.对一次区域教研说题比赛进行简单介绍，并结合说题比赛给出两点体会：说题——向问题更深处漫溯；说题——功夫重在“说”外.

说题比赛；区域教研；深层结构；重在“说”外

近日有幸拜读《中国数学教育（初中版）》2015年第4期和第6期刊登的与说题相关的教研论文，读后受益匪浅，更为笔者于暑假期间参加的一次山东省东营市胜利教育管理中心的区域教研说题比赛提供了范本.现结合本次说题比赛及说题后备课组的集体讨论，简单谈几点体会，权当抛砖引玉，欢迎各位专家和同行批评指正.

本次说题比赛共有两个环节：第一个环节是制作说题课件（时间160分钟）；第二个环节是现场说题（时间20分钟），两个环节时间共计3个小时.在拿到题目以后，笔者发现是本地区（东营市）2014年中考试题最后一题的改编题，便确定了以日常积累的与此相关的中考试题开展题目变式的说题主线（下文提及的相关中考试题的地区、年份、题号为后续所加），同时确定了说题的基本流程：说题目、说背景；说教法、说学法；说解法、说变式；说总结、说反思.

一、说题比赛

1.说题目，说背景

探究发现

如图1，四边形ABCD是正方形，∠AEF=90°，EF交正方形外角平分线CF所在的直线于点F.当E是BC的中点时，有AE=EF成立.

数学思考

某数学兴趣小组在探究AE，EF的关系时，运用“从特殊到一般”的数学思想，通过验证得出如下结论：当点E是直线BC上（点B，C除外）任意一点时（其他条件不变），结论AE=EF仍然成立.

假如你是该兴趣小组中的一员，试从“点E是线段BC上的任意一点”“点E是线段BC延长线上的任意一点”“点E是线段BC反向延长线上的任意一点”三种情况中，任选一种情况，在图2中画出图形，并进行证明.

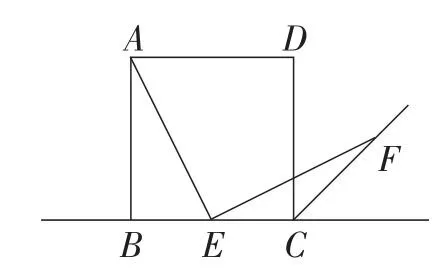
图1

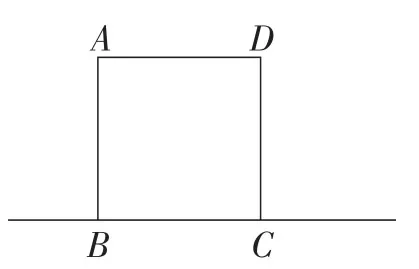
图2

（1）源于教材，高于教材.

此题是根据2014年山东省东营市中考试题第24题进行改编的，其最初的原型为教材八年级下册第69页第14题.

原型 如图3，四边形ABCD是正方形，E是边BC的中点，∠AEF=90°，且EF交正方形外角的平分线CF于点F.求证：AE=EF.

提示：取AB的中点G，连接EG.

（2）知技并重，动静结合.

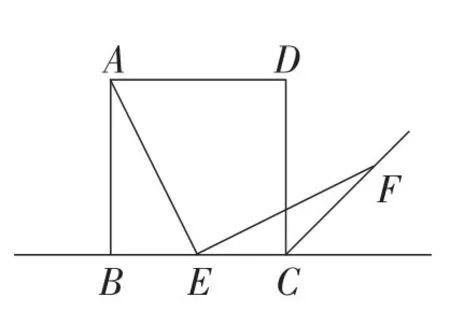
图3

此题是动态问题的典型问题，关键是从特殊（静态）位置到一般位置的视角发现问题的本质；主要考查了正方形的性质、全等三角形的性质与判定等知识，集中考查核心考点于一题；此外，此题还注重了对类比、一般与特殊、化归与转化、分类讨论等相关数学思想的考查，重在培养学生解决类似问题的能力.

2.说教法，说学法

在教学过程中主要采用启发教学法，重在引导学生体会从特殊到一般的过程中的“变化中的不变”，同时引导学生回忆相关几何知识，因此此题教学的重点是综合运用相关几何知识解决“动点”问题.

在学法上主要采用自主探究和小组合作的形式，使学生在自主探究中体验学习数学的乐趣，在解决问题的过程中欣赏几何变化的“美”，在小组合作中培养学生合作的态度和意识.显然，此题教学中的关键是如何添加相应的辅助线，进而解决问题，因此此题教学的难点是：灵活添加辅助线，进而顺利解决几何问题中的“动点”问题.

3.说解法，说变式

解：（方法1）（1）点E在线段BC上.在线段AB上取点G，使 AG=CE，连接 EG，证明△AEG≅△EFC即可（如图4）.

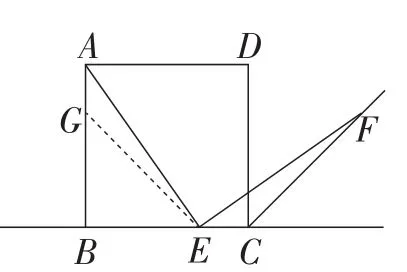
图4

（2）点E在线段BC的延长线上.在线段AB的反向延长线上取点G，使AG=CE，连接EG，证明△AEG≅△EFC即可（如图5）.

点E在线段BC的反向延长线上.在线段AB的延长线上取点G，使AG=CE，连接EG，证明△AEG≅△EFC即可（如图6）.

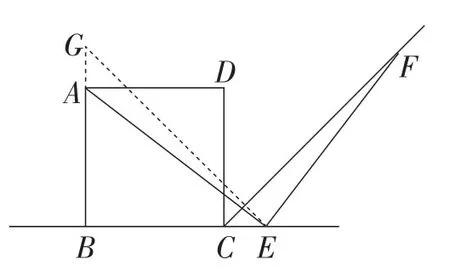
图5

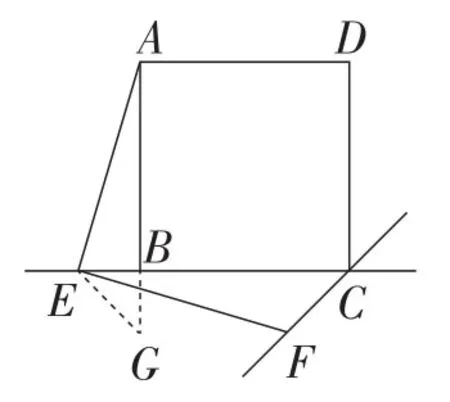
图6

【说明】可以看出上述解法给出的辅助线的添加方式是高度统一的，以及所要证明的一对全等三角形(△AEG≅△EFC)也是一致的，包括其证明的方法ASA (∠EAG=∠FEC，AG=EC，∠AGE=∠ECF)也是相同的.

图4中因为∠EAG+∠AEB=90°，∠FEC+∠AEB=90°，所以 ∠EAG=∠FEC.又因为 ∠AGE=∠ECF=135°，而AG=EC易得.

图5中因为 ∠EAG=∠ABC+∠AEB=90°+∠AEB (∠EAG-∠AEB=90°)，∠FEC=∠AEF+∠AEB=90°+∠AEB(∠EAG-∠AEB=90°)，所以 ∠EAG=∠FEC.又因为∠AGE=∠ECF=45°，而AG=EC易得.

图6中因为∠EAG+∠AEB=90°，∠FEC+∠AEB=90°，所以 ∠EAG=∠FEC.又因为 ∠AGE=∠ECF=45°，而AG=EC易得.

问题1：作出△AEF的外接圆，你有何发现呢？点C在这个圆上吗？

发现A，E，F，C四点共圆.

解：（方法2：几何画板软件演示，此处只呈现三种不同位置的静态图形）（1）点E在线段 BC上.显然 ∠AFE=∠ACE=45°（同弧所对的圆周角相等），在△AEF中，∠AEF=90°，所以∠FAE=45°.进而△AEF是等腰直角三角形，从而命题得证（如图7）.

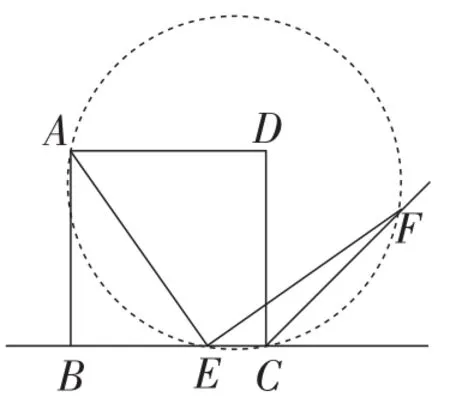
图7

（2）点E在线段BC的延长线上和反向延长线上.略（如图8和图9所示）.

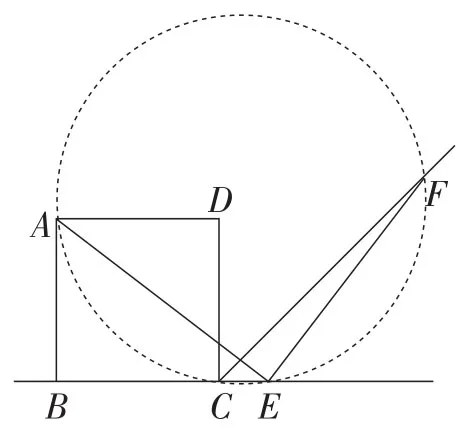
图8

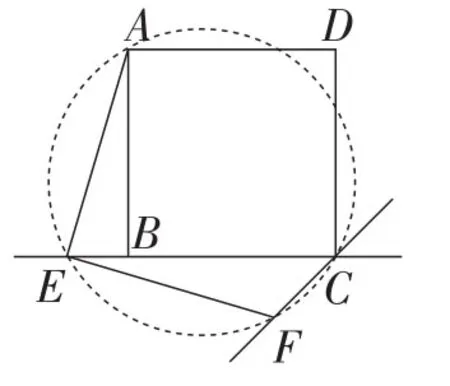
图9

变式1：2010年山东·黄岗卷第18题（略）.

问题2：原题中正方形ABCD改为正△ABC，相关结论还成立吗？

变式2：2014年山东·东营卷第24题（略）.

问题3：原题中正方形 ABCD改为正 n边形ABC…X，相关结论还成立吗？

变式3：2010年江苏·无锡卷第26题（略）.

问题4：在正方形的条件下，将结论AE=EF与条件CF是角平分线互换，是否仍然成立？在正三角形的情况下呢？

变式4：2014年广西·北海卷第25题和2014年广西·南宁卷第25题（略）.

【说明】该变式仍然可以采用上述方法1中图4、图5、图6的辅助线的添加方式，同样证明△AEG≅△EFC，只不过证明三角形全等的方法SAS (AE=EF，∠EAG=∠FEC，AG=EC)发生了变化而已，不用采用参考答案所给的解题方法而另起炉灶.

参考答案所给解题思路如图10、图11、图12（证明△ABE≅△EGF，进而说明△CGF是等腰直角三角形即可）.

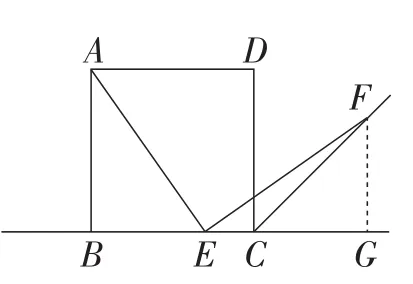
图10

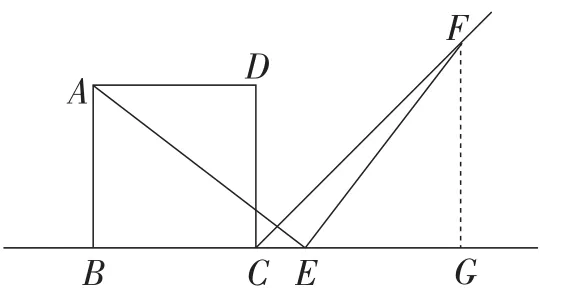
图11

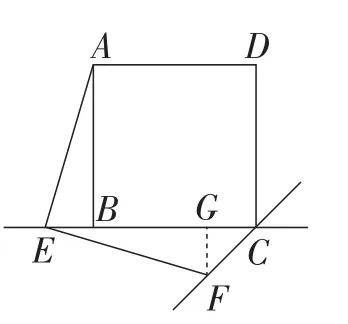
图12

问题5：与平面直角坐标系相结合.

变式5：2013年湖北·孝感卷第25题（略）.

4.说总结，说反思

“动点”问题就是在三角形、四边形、圆等一些几何图形上，设计一个或两个动点，点的运动引起一些图形形状变化的问题，其在变化过程中伴随着数量关系、位置关系、图形的特殊状态、图形间的特殊关系等.这类问题综合性强，考查全面，常常集几何、代数于一体，主要体现数形结合或分类讨论的思想，同时在解题过程中要通过实验、操作、观察和想象的方法掌握运动的本质，发现“变化中的不变”，进而解决问题.

二、说题体会

1.说题——向问题更深处漫溯

（1）一题多解.

条条大路通罗马.解数学题也是如此，一道题目会有很多种解法，哪种解法是最好的？哪种解法是最自然的？这取决于教师日常的积累和教师的知识储备.上述说题过程中提供了两种方法：一种是利用全等三角形；另一种利用了“辅助圆”，就解题而言都是不错的方法.在说题后的备课组讨论中，有的教师又提供了另外一种方法，需要用到高中平面向量的相关知识，在此以点E在线段BC上为例进行简单介绍.

解：（方法3）建立如图13所示的平面直角坐标系.

设正方形ABCD的边长为1，点A的坐标为A(0，1)，点E的坐标为E(m，0)，点F的坐标为F(n，n-1)，其中0＜m＜1，n＞1.

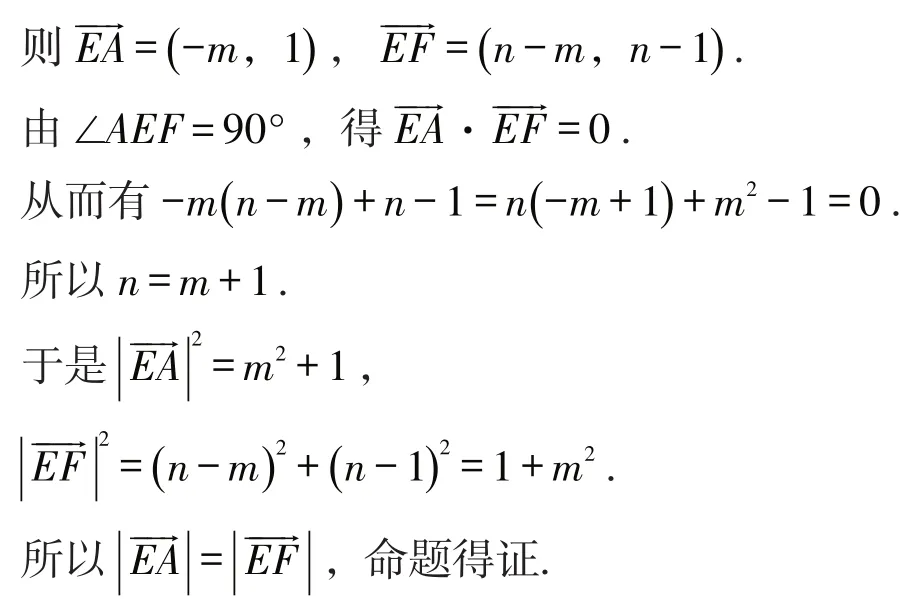
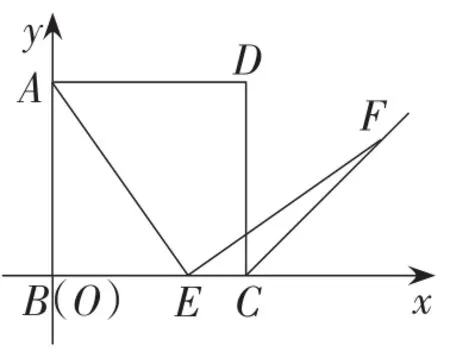
图13

（2）一题多变.

数学题，万变不离其宗.在上述说题中提供了五种变式，都是相关地区的中考试题，可见研究中考试题的必要性.但是“题目是永远做不完的”，这就要求一线教师要做大量的题目，完成积累，进行总结，从而在课堂教学中实现一题多变、触类旁通、举一反三，真正达到“学生减负，课堂增效”的目的.

（3）由浅入深.

对数学问题的求解，实质上是对问题结构的一种认识或揭示.对客观存在着的问题结构，人们的认识会有深有浅，罗增儒教授对解题教学有着独到的见解，提倡在解题教学中挖掘题目的“深层次结构”，上述说题过程中就体现了由浅入深的过程，让我们认识到了问题的深层次结构（方法2）.

2.说题——功夫重在“说”外

（1）说题要求说题者具备善于发现的眼睛.

法国著名雕塑家罗丹曾经说过，世界上并不缺少美，只是缺少发现美的眼睛.笔者认为这句话同样适用于数学教学，特别是几何的教学，漂亮的几何图形构成了完美的世界，这正是渗透数学美、欣赏数学美的大好时机.《义务教育数学课程标准（2011年版）》不止一次提到“欣赏”一词，更是指出：激发学习数学的兴趣，欣赏数学的优美.上述说题如果转化为课堂教学，我们应该引导学生体会“变中的不变”，发现数学的“美”，用欣赏的眼光去看待解题，从而提高学生学习数学（特别是解题）的积极性和主动性.

（2）说题要求说题者具备善于关联的头脑.

20世纪伟大的几何学家陈省身指出：好的数学指的是能发展的、能越来越深入、能被广泛应用、相互联系的数学.上述说题案例就是一个充分关联的题目，它自身集三角形、全等三角形、圆于一体，可以考查学生各方面的综合能力，涉及到教师的说题，就对教师提出了更高的要求，从上述说题提到的不同解法、不同变式可以发现这都需要一线教师在日常教学中善于积累、善于关联，善于将相同或类似的题目放在一起，这样在说题比赛中才不会“捉襟见肘”，才会“得心应手”.

（3）说题要求说题者具备勤于动笔的双手.

数学只看不想是行不通的，只看只想也是不行的，正所谓“纸上得来终觉浅，绝知此事要躬行”.上文提到的发现、积累、关联都离不开最基本的动手，我们在日常教学中就要勤于动笔、勤于动手，将所看、所思、所想付诸实践，在说题过程中才会有意想不到的收获.

三、结束语

说题是最近一段时间比较流行的教研形式，它不仅能够考查一位教师的解题能力，还能够考查一位教师的课堂教学组织能力，因此备受教研部门青睐.同时，它又是对广大一线教师的一种督促，杜绝以前那种“题目来了直接看答案或上网查答案”的陋习，督促一线教师提高解题能力，因此备受一线教师喜爱.

［1］李云萍，方晓飞.说题说出别样天：摭谈初中数学教师说题［J］.中国数学教育（初中版），2015（4）：26-29.

［2］余中华.精准的阐述，源于对题目的透彻理解：一次说题比赛引发的思考［J］.中国数学教育（初中版），2015（6）：24-27.

2017—02—06

山东省教育科学十二五规划重点课题——基于新课程的反思性课堂建设研究与实践（2011J2009）；东营市教育科学十二五规划课题——“导学·反思”和谐高效课堂教学的实践与研究（125DYJG210）.

于彬（1984—），男，中学一级教师，主要从事初中数学教学研究.