初中课程标准中方程内容的国际比较研究
尚亚明,张玉环
( 1.华东师范大学数学系; 2.河南大学数学与统计学院)
初中课程标准中方程内容的国际比较研究
尚亚明1,2,张玉环2
( 1.华东师范大学数学系; 2.河南大学数学与统计学院)
文章比较分析了12个国家的课程标准中的方程内容,采用定量和定性相结合的研究方法对这些国家数学课程中方程内容的广度、各主题的知识分布和比重,以及知识点的认知要求分布进行比较,以便了解不同国家对方程内容的设置情况.
初中方程;国际比较;聚类分析
一、问题的提出
美国著名的课程与教学研制专家泰勒将课程与教学的基本原理归纳为4个问题:学校应力求达到何种教育目标?如何选择有助于实现这些目标的学习经验?如何有效地组织这些学习经验?如何评估学习经验的有效性?研究者普遍认为,教师在日常教学中相当依赖教材,在很大程度上依据所使用的教材而决定教什么、怎么教,以及给学生布置哪些习题等.由此看来,课程标准是一门学科的主线,决定了教材的编写和教师教什么,学生学什么.初中数与代数部分的内容有数、式、方程和函数等,其中方程起到承前启后的作用,前承数与式的学习,后启不等式和函数的学习.方程是初中数学内容中最基本的概念,也是初中数学最重要的核心内容之一,方程的应用思想贯穿整个初中数学课程.世界上各国的初中数学课程标准对方程的内容是如何分布的,是我们需要研究的问题.
二、研究设计
1.研究问题
本文选取世界上经济或教育比较发达的国家,以知识主题和知识点的认知要求为切入点,针对初中数学课程标准中的方程内容进行比较分析.具体来说,主要研究以下几个问题:各个国家课程标准中方程内容的广度如何?在各主题上的知识分布和比重如何?各个国家的知识点在不同认知要求的分布如何?方程的应用具体涉及到哪几个部分,以及各个国家的涉及情况怎样?各个知识点的受重视情况如何?
2.研究国家和课程标准的选取
本文选取了下列五大洲的12个国家的初中数学课程标准作为研究对象.亚洲:中国、日本、韩国、新加坡;欧洲:英国、法国、芬兰、德国;美洲:美国、加拿大;非洲:南非;大洋洲:澳大利亚.这12个国家来自不同的洲,经济、教育、科技、文化的发展程度也不同,能很好地展示世界各地数学课程中的方程内容的特点.所选取的初中数学课程标准主要来源于曹一鸣教授主编的《十三国数学课程标准评介(初中卷)》(中国的选用《义务教育数学课程标准(2011年版)》),对于所选课程标准的原则是:大部分初中生升入高中时所必需的基础内容,不涉及选修内容.具体选择的版本如表1所示.

表1:初中方程内容国际比较样本
3.研究方法
主要用定量分析中的统计分析法和定性分析法中的比较分析法对各国知识点进行统计和比较,用spss软件对知识点的分类进行聚类分析.
(1)知识点的界定.
广度、认知要求的统计涉及到知识点的界定,由于我国课程标准方程部分的内容比较系统和清晰,本文就我国初中课程标准方程内容为主,综合其他11个国家的数学课程标准中的方程内容,将方程内容分为四大知识主题:①方程概念及其性质;②一元一次方程;③二元一次方程组;④一元二次方程.参考12个国家的课程标准,列出各个知识主题的知识点,然后进行比较、归纳,最后调整成完善的知识框架,统计出各个知识点及认知要求水平.
(2)广度.
内容广度是指课程内容所涉及的领域和范围的广泛程度,用知识主题所包含的知识点个数来表示.
(3)认知要求.
许多国家的课程标准并没有对课程内容的要求做出明确的划分层次,本文参考新修订的布卢姆教育目标分类学,并参考我国对教学内容要求的划分层次,提出认知要求的分类如表2所示.

表2:认知要求指标
(4)聚类分析.
本文采用系统聚类法进行聚类分析.系统聚类的基本思想是:距离相近的样品(或变量)先聚成类,距离相远的后聚成类,过程一直进行下去,每个样品(或变量)总能聚到合适的类中.系统聚类方法包括组间连接法、组内连接法、最近距离法、最远距离法等,本文选择spss系统默认方法——组间连接法.聚类分析能客观、综合地把整个方程知识体系的知识点分类,从而得出每个知识点的受重视情况,这是普通分类方法所达不到的.
三、研究过程与结果
1.总广度的比较
对12个国家的方程内容进行知识点的广度分析,总广度由大到小排名如图1所示,依次是中国、韩国、日本、新加坡、德国、英国、美国、澳大利亚、加拿大、芬兰、法国、南非.韩国的知识点数仅次于中国,且两者差距不大.就具体的原因而言,韩国在2006年之前经历了7次数学教育改革,第七次数学教育改革的课程比以往减少了30%的教学内容,但内容的减少和课时的减少并没有解决学生的学习负担问题,所以此次的教育改革适当调整了一些内容,使其更具合理性.从整体上看,大部分国家在方程部分的知识点数大同小异,其中,德国、新加坡两国的知识点数都是13,排在第4名.

图1
2.各主题知识分布的比较
(1)“方程概念及其性质”主题的知识点分布.
从涉及到的知识点来看,各国课程标准在“方程概念及其性质”主题的知识点分布无太大差别.表3统计了12个国家在该知识主题的知识点分布情况.
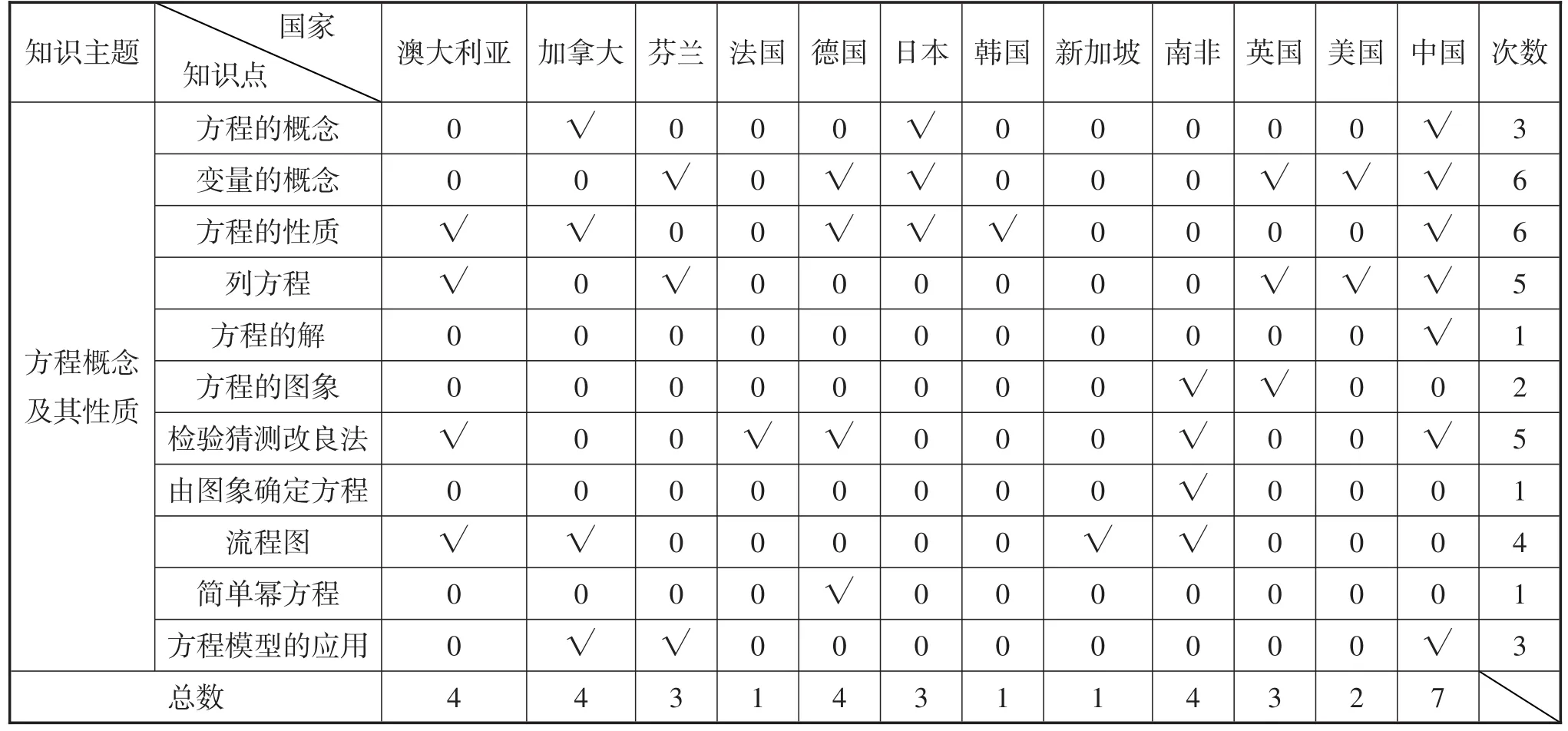
表3:“方程概念及其性质”主题的知识点分布
从表3中可以看出:①12个国家的课程标准都有该部分的知识点,知识点个数大同小异,且中国在这部分的广度最大,其次是澳大利亚、加拿大、德国、南非,相比之下,法国、韩国、新加坡在该部分的知识点数较少;②出现了一些只存在在某个国家的知识点,如德国的“简单幂方程”、南非的“由图象确定方程”、中国的“方程的解”;③5个及5个以上国家的课程标准都有一些共同知识点:变量的概念、方程的性质、列方程、检验猜测改良法,说明这些知识点是该部分的核心知识点.
(2)“一元一次方程”主题的知识点分布.
一元一次方程是最简单的方程.对12个国家的课程标准在该知识主题的知识点进行统计,得到表4.

表4:“一元一次方程”主题的知识点分布
从表4可以看出:①除了南非,其余11个国家在该主题都有知识点.韩国在该主题有5个知识点,广度最大,其次是美国和中国,有4个知识点,法国、新加坡、英国并列第三,都有3个知识点;②11个国家的课程标准都有一个核心知识点:解一元一次方程;③但从中国的课程标准来看,该主题的知识点数处于中等水平,除了有“解一元一次方程”这个核心知识点外,还出现了“解可以化为一元一次方程的分式方程”这个大部分国家都没有涉及到的知识点.
(3)“二元一次方程组”主题的知识点分布.
二元一次方程组是连接行列式、矩阵等的基础桥梁,是初中方程的核心知识主题.表5统计了12个国家课程标准在该主题的知识分布.
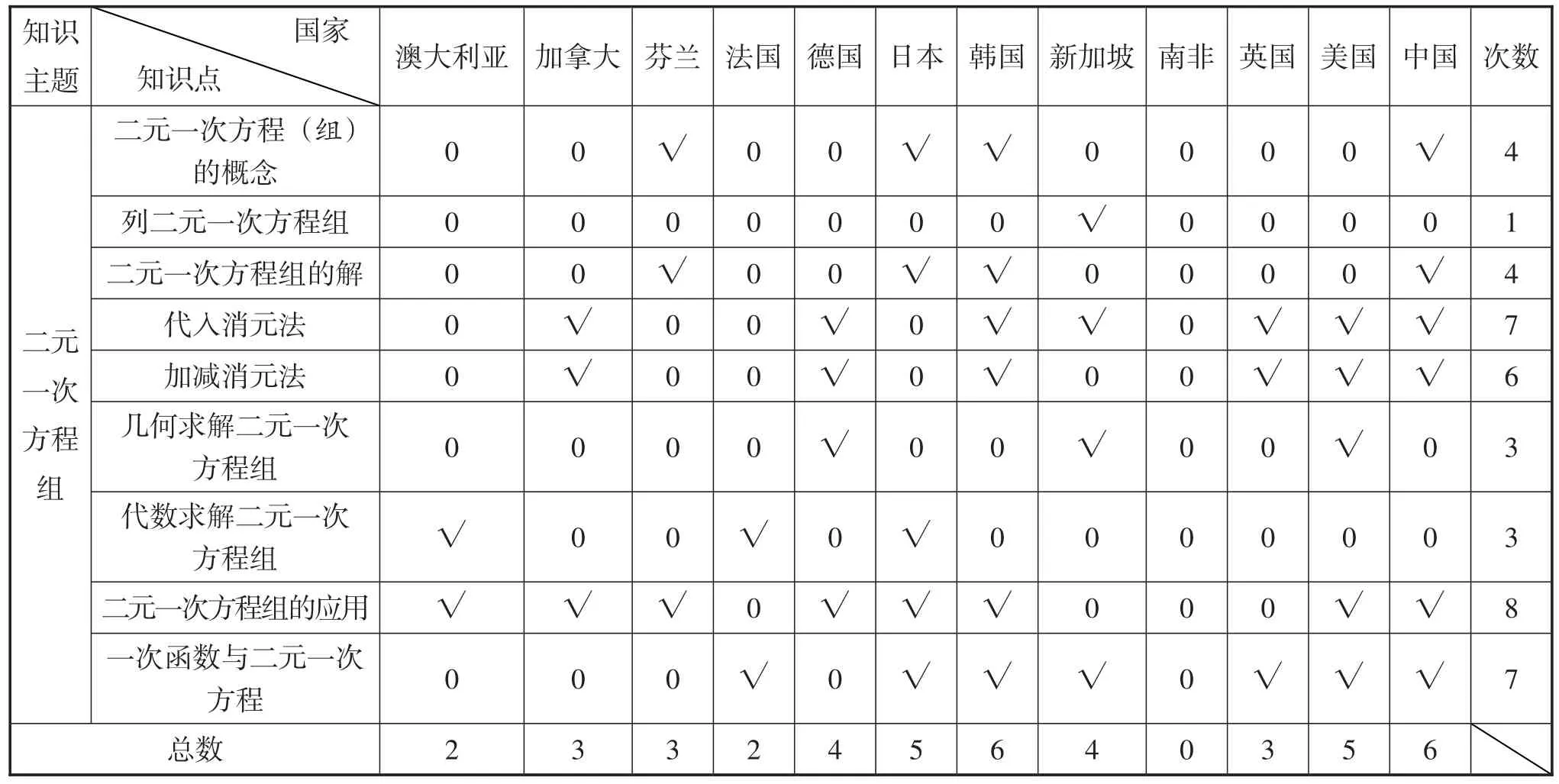
表5:“二元一次方程组”主题的知识点分布
从表5可以看出:①南非在该主题没有知识点,其余各国的课程标准在该部分的知识点数不相上下,广度最大的是韩国和中国;②从具体的知识点来看,5个及5个以上国家的课程标准都共有的知识点是:代入消元法、加减消元法、二元一次方程组的应用、一次函数与二元一次方程,表明这些知识点是该主题的核心知识点.
(4)“一元二次方程”主题的知识分布.
一元二次方程是最基本的非线性方程.表6统计了12个国家的该主题的知识分布.
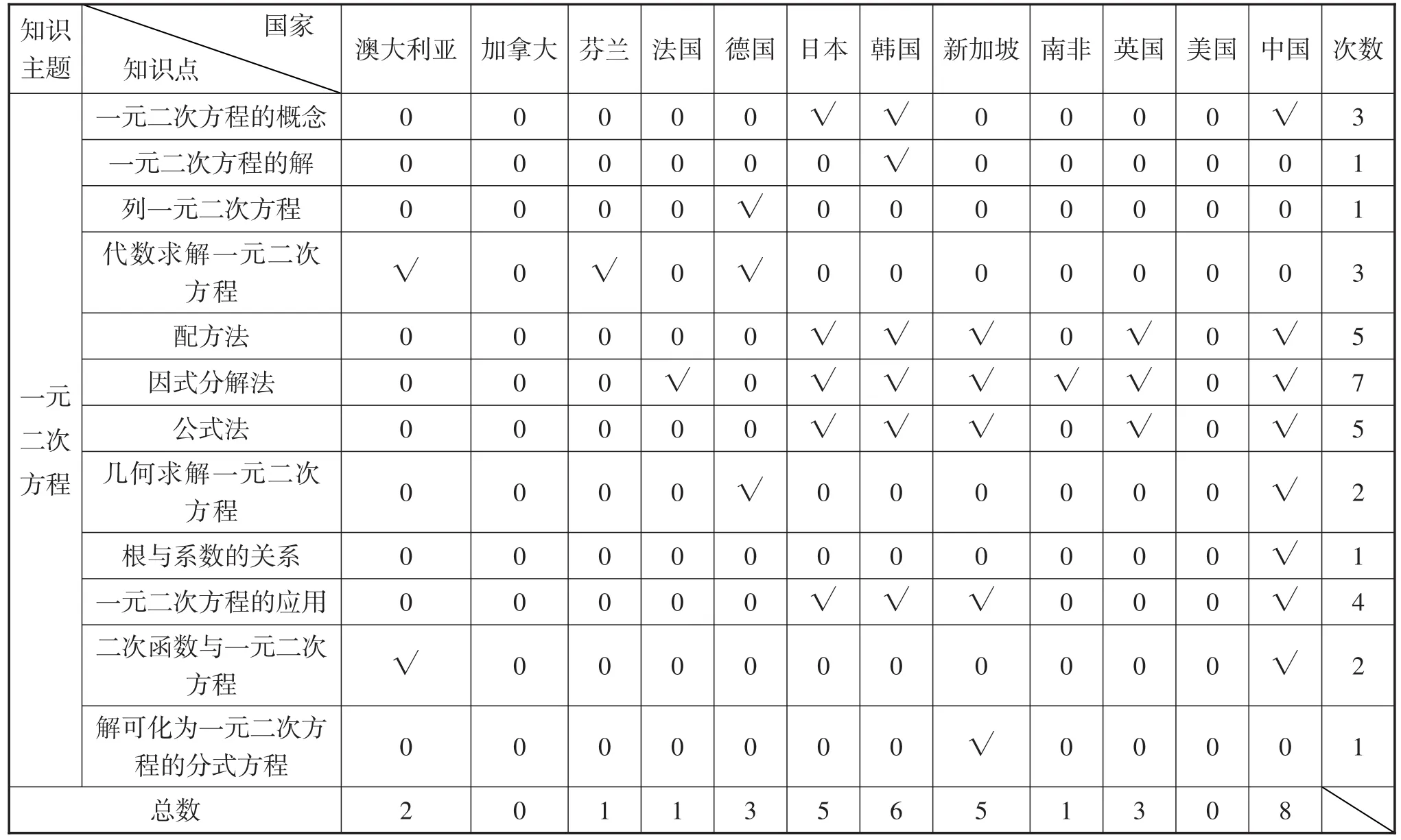
表6:“一元二次方程”主题的知识点分布
从表6可以看出:①加拿大和美国的课程标准没有该主题的知识点,中国在该主题的知识点数最多;②存在一些只有某个国家才有的知识点,如韩国的“一元二次方程的解”、德国的“列一元二次方程”、中国的“根与系数的关系”(不作要求,学有余力)、新加坡的“解可化为一元二次方程的分式方程”;③出现次数最多的知识点是“因式分解法”,其次是“公式法”“配方法”,说明这3个知识点是核心知识点;④但看中国的课程标准,中国在该主题出现了一些只有本国或少数国家才有的知识点:根与系数的关系(不作要求,学有余力)、解可化为一元二次方程的分式方程、二次函数与一元二次方程、几何求解一元二次方程.
3.各课程标准在四个知识主题上的广度所占比重的比较
对12个国家的课程标准的四个主题的广度占方程内容总广度的百分比进行统计,得到图2.其中,对各国课程标准中比重最大的主题所对应的数据加黑,以便比较.
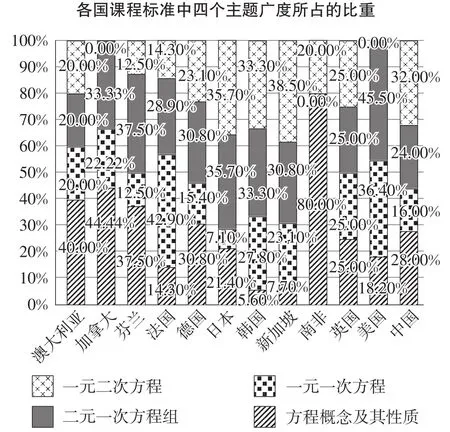
图2
从图2可以得到以下结论.
①各国课程标准中比重最大的主题集中在“方程概念及其性质”“二元一次方程组”,以及“一元二次方程”三个知识主题上,这说明初中方程内容的重点是“方程概念及其性质”“二元一次方程组”和“一元二次方程”,“一元一次方程”只是作为基础辅助.
②除了加拿大、美国、南非,其他国家的方程课程的基本内容是一样的,都包含了“方程概念及其性质”“一元一次方程”“二元一次方程组”“一元二次方程”四个主题.其中,所有国家都涉及到的知识主题是“方程概念及其性质”,这表明,此部分的内容是初中方程课程中最基本的内容.
4.方程内容的认知要求分布比较
对12个国家课程标准方程部分不同认知要求的知识点进行统计(“方程模型的应用”“一元一次方程的应用”“二元一次方程组的应用”“一元二次方程的应用”除外),得到图3.同样地,对比重最大的认知层次所对应的数据加黑,以便于比较.从中可以得到:(1)在四个认知层次上都做要求的国家只有美国和中国,其余国家只涉及到两个或三个认知层次;(2)除了芬兰,其余各国方程课程的认知要求都侧重“掌握”层次,说明初中方程内容的大部分知识点都要求达到“掌握”层次.
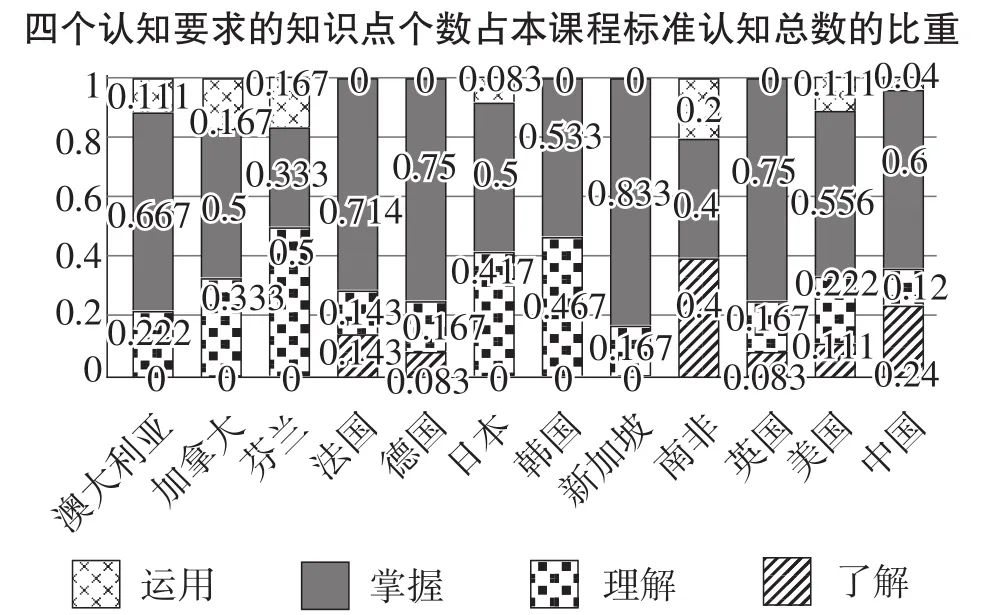
图3
5.方程应用的涉及比较
学会用方程解决问题是初中生学习方程的最终目的,表7统计了12个国家课程标准对于方程应用的涉及情况.

表7:方程应用的涉及比较
从表7可以看出:应用涉及到四个部分:方程模型的应用、一元一次方程的应用、二元一次方程组的应用、一元二次方程的应用.大部分课程标准都有“二元一次方程组的应用”,说明二元一次方程组在解决实际问题中的作用不容忽视.
6.各个知识点的受重视情况
对所有的知识点按照认知要求进行系统聚类(“方程模型的应用”“一元一次方程的应用”“二元一次方程组的应用”“一元二次方程的应用”除外),得到聚类谱系,如图4所示.
图4左边的两列数字对应相应的知识点.根据实际情况,分为4类:G1={4,12},G2={9},G3={14,20,21},G4={1,2,3,4,5,6,7,8,10,11,12,13,15,16,17,18,19,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36}.结果就是G1={列方程,列一元一次方程} ;G2={流程图} ;G3={解一元一次方程,代入消元法,加减消元法} ,其他的知识点就是第4类.
计算各类知识点的平均要求指标,指标越大的就越受重视.得出最受重视的知识点有:解一元一次方程、代入消元法、加减消元法;其次是列方程、列一元一次方程;最后是流程图.最不受重视的知识点有:方程的概念、变量的概念、方程的性质、方程的解、方程的图象、检验猜测改良法、由图象确定方程、简单幂方程、一元一次方程的概念、一元一次方程的解、解可化为一元一次方程的分式方程、一次函数与一元一次方程、二元一次方程组的概念、列二元一次方程组、二元一次方程组的解、几何求解二元一次方程组、代数求解二元一次方程组、一次函数与二元一次方程、一元二次方程的概念、一元二次方程的解、列一元二次方程、代数求解一元二次方程、配方法、因式分解法、公式法、图象求解一元二次方程、根与系数的关系、二次函数与一元二次方程、解可化为一元二次方程的分式方程.
四、思考与总结
我国新的义务教育数学课程标准从2012年颁布,到目前为止,已经进行了几年的实践,通过国际比较研究来进一步深入研究初中数学方程课程,为我国新的初中数学课程的改革提供基础.通过本文的研究,我们可以更为准确地把握我国方程内容的广度、各知识主题的知识点分布和比重、认知要求的分布,以及知识点的分类情况.他山之石,可以攻玉,比较研究的目的不是照搬其他国家的经验,而是取其精华来完善自己.
1.对于知识点,把握共性,体现个性
通过以上比较可以发现:中国的总广度最大,知识点数最多.从具体的知识点来看,各个国家大同小异,对于一些基础、核心的知识点,大多数国家都有涉及,各个国家的教育现状不同,对于知识点的选取也不同,但如何把握共性,又能体现本国的个性是一个很有挑战意义的任务.
2.认知层次多元化
多元文化的提出是相对于传统的、单一的文化而言的.11个国家的课程标准中方程内容的认知要求都偏重于“掌握”层次,在四个认知层次上都做要求的只有美国和中国,其余国家只涉及到两个或三个认知层次.《义务教育数学课程标准(2011年版)》指出:课程内容要反映社会的需要、数学的特点,要符合学生的认知规律.课程内容的呈现应注意层次性和多样性.
3.注重方程的应用意识
所有国家都不同程度地涉及到了方程的应用,尤其是二元一次方程组的应用.《义务教育数学课程标准(2011年版)》明确指出:建立和求解模型的过程包括:从现实生活或具体情境中抽象出数学问题,用数学符号建立方程、不等式、函数等表示数学问题中的数量关系和变化规律,求出结果并讨论结果的意义.我国的数学课程很重视培养学生的数学应用意识,方程的应用也不例外,且方程在中学阶段的学习中起到承上启下的作用.因此,注重方程的应用意识尤为重要.
[1](美)Ralph W.Tyler.课程与教学的基本原理[M].罗康,张阅,译.北京:中国轻工业出版社,2008.
[2]姜美玲.教师实践性知识研究[M].上海:华东师范大学出版社,2008.
[3]于莉.基于模型思想的初中方程教学设计研究[D].重庆:重庆师范大学,2013.
[4]曹一鸣.十三国数学课程标准评介(初中卷)[M].北京:北京师范大学出版社,2013.
[5]中华人民共和国教育部制定.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012.
[6](美)L·R·安德森.学习、教学和评估的分类学、布卢姆目标分类学(修订版)[M].上海:上海师范大学出版社,2008.
[7]朱建平.应用多元统计分析(第二版)[M].北京:科学出版社,2012.
[8]张勤琼,张维忠.多元文化下的方程求解[J].数学教育学报,2007,16(4):72.
2017—02—01
河南省教师教育课程改革研究项目——多元化学习评价在高校数学类教师教育理论课程的实践与探索(2016-JSJYYB-012);
河南大学第十六批教学改革项目——国家教师资格统一考试背景下数学师范生课程体系与教学内容改革研究与实践(HDXJJG2016-075);
河南大学民生学院教育教学改革研究项目——《概率论与数理统计》课程的学习成绩归因分析及对策研究(MSJG2015025).
尚亚明(1991—),女,博士研究生,主要从事数学教育研究.

