不同焦距的连续像对相对定向严密公式

李忠美，边少锋，纪 兵

(海军工程大学导航工程系，湖北 武汉 430033)

不同焦距的连续像对相对定向严密公式

李忠美，边少锋，纪 兵

(海军工程大学导航工程系，湖北 武汉 430033)

针对现有解算相对定向元素的公式通常用于具有相同焦距的立体像对这一现状，为充分利用不同相机所拍摄的现有影像信息，以像点坐标作为观测量，给其加入改正数，借助计算机代数系统对共面方程进行严格的线性化，推导出了适用于解算不同焦距立体像对相对定向元素的严密公式；最后，通过算例验证了该方法的正确性，可在一定程度上丰富摄影测量理论。

摄影测量；立体像对；相对定向；共面方程；线性化

立体像对的相对定向就是要恢复摄影时相邻两影像摄影光束的相互关系，一种是单独像对相对定向，它采用两幅影像的角元素运动实现相对定向；另一种是连续像对相对定向，它以左影像为基准，采用右影像的直线运动和角运动实现相对定向[1-4]。多个连续模型的处理中通常采用连续法相对定向。在传统的连续像对相对定向中，多考虑理想的情况，将角元素视为小角，因此大大简化了共面方程的线性化结果，得到近似的相对定向平差模型[5]。但是当连续像对相对定向法用于航偏角大的长航带时，有可能会使后续像对的相对定向κ角偏大，以至于传统的公式不能再使用。此时应该考虑更严密的解法，将像点坐标视为观测量，如文献[6—7]便将像点坐标而非上下视差作为观测量，给其加入改正数，对共面方程进行严格的线性化，这种更严密的相对定向解法可适用于偏航角大的长航带。然而，现有文献中关于相对定向的研究多是针对同一航带中的相同相机所拍摄的立体像对，即两张像片具有相同的焦距[8-10]。实际上，随着摄影测量影像获取方式的多样化[11-12]，覆盖同一地区的影像并非仅来源于同一相机，此时需研究不同焦距情况下的相对定向方法,如文献[13]将右片焦距作为待求参数，将相对定向元素个数增加至6个，然后通过将共面方程线性化，推导出了一种适用于可变焦距的相对定向公式，该公式适用于仅知一张像片焦距的情况。受以上文献启发，为充分利用不同相机所拍摄的现有影像信息，丰富摄影测量理论，本文将在现有文献的基础上，推导出适用于解算不同焦距的连续像对相对定向元素的公式。

1 共面方程及其线性化

1.1 共面方程表示

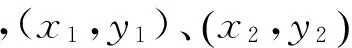
(1)

式中

(2)

另外，由于旋转矩阵通常表示为φ、ω、κ转角系

统，如下

图1 相对定向示意图

(3)

将式(2)、式(3)代入式(1)中，可知共面方程中包含6个未知变量bX、bY、bZ、φ、ω、κ。由于bX仅影响相对定向模型大小，而不影响模型的建立，故可得相对定向元素为5个待求参数bY、bZ、φ、ω、κ。

1.2 共面方程线性化

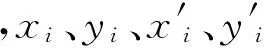
AiV+BiX+F0i=0

(4)

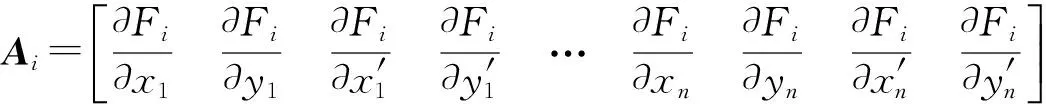
可借助计算机代数系统，推导出系数矩阵Ai、Bi中的各元素如下

2 最小二乘平差

2.1 计算过程

每对同名点可列1个形如式(4)的方程，由于相对定向元素为5个，当有5对观测点时即可列出5个方程，求出5个待求参数。为了保证精度，通常进行多余观测，然后借助最小二乘平差对其进行解算。由于像点坐标与相对定向元素同时作为模型中的未知量参与平差，故可根据附有参数的条件平差法[14-15]解算相对定向元素。主要步骤为：

(1) 记观测权矩阵为P，为求出满足VTPV=min的一组解，按求函数条件极值的方法，组成函数

(5)

式中，K是条件数。为求Φ的极小值，将其分别对V和X求一阶导数，并令其等于零，可得

(6)

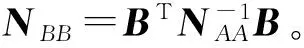
(3) 将相对定向元素改正数与限差相比，若小于限差，则改正数与初始近似值之和即为相对定向元素的值。否则，重复步骤(2)、(3)。反复趋近，直至改正数小于限差。

2.2 精度评定

由于每对同名点可列1个形如式(4)的方程，而待求参数个数为5个，则必须观测5对同名点可唯一确定待求参数。因此可根据文献[15]，得单位权中误差的估值

(7)

则所求相对定向元素的精度为

(8)

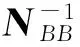
3 算例分析

为验证本文算法的正确性及可靠性，以下通过两组算例对其进行验证。其中，算例1和算例2采用的数据分别为不含与包含观测噪声的像对。数据如下：已知左、右像片(A为小航偏角像对、B为中航偏角像对、C为大航偏角像对)的外方位元素真值见表1，在某区域范围内选取9个地面点见表2，利用共线方程，可分别计算它们在左、右像片上对应的像点坐标(认为各像点坐标为等精度观测)。

3.1 算例1(不含观测噪声像对的相对定向)

分别根据9对像点坐标，令BX=200 m，可利用本文连续像对相对定向公式解算小航偏角、中航偏角、大航偏角像对的相对定向元素，并将结果列于表3。

由表3可以看出，在像点坐标不含有观测误差时，利用本文方法分别对不同焦距的小航偏角、中航偏角、大航偏角像对进行连续相对定向，解算结果与真值相比，差异可忽略不计。此外，由于文中将像点坐标作为观测量，且对相对定向元素的求导过程中不存在小角近似简化。因此，该方法理论严密，且可用于解算大航偏角像对的相对定向元素。

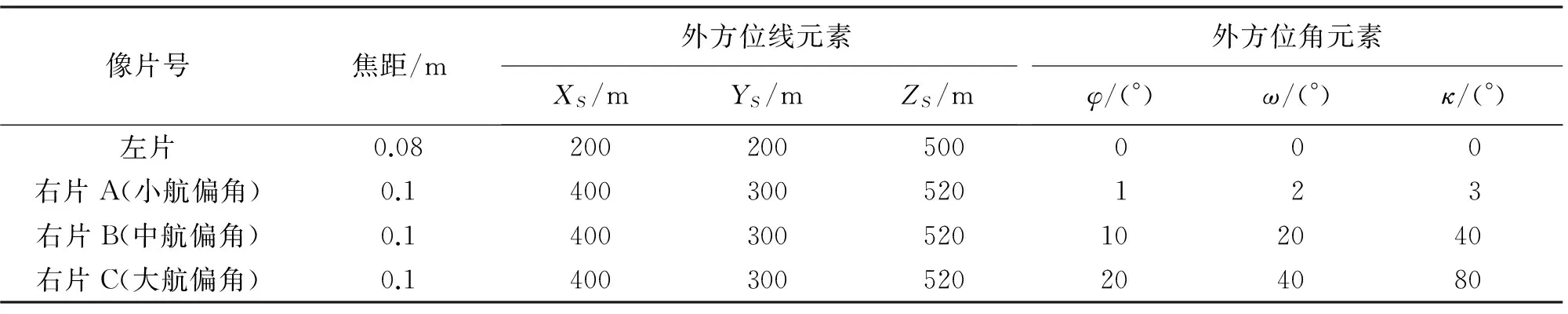
表1 像对的外方位元素值

表2 地面点坐标值 m

表3 不含观测噪声连续像对的相对定向结果

3.2 算例2(含有观测噪声像对的相对定向)

分别为9对像点坐标上加上0.5像素的量测误差(像元大小为6 μm)，然后令BX=200 m，利用本文相对定向方法解算小航偏角、中航偏角、大航偏角像对的相对定向元素，并将结果列于表4。

表4 包含观测噪声连续像对的相对定向结果

由表4可以看出，在像点坐标含有0.5像素误差时，利用本文方法进行连续像对相对定向元素解算时，与真值相比，小航偏角、中航偏角、大航偏角像对的相对定向角元素均可达到秒级精度，而小航偏角像对的相对定向线元素可达到毫米级精度，中航偏角、大航偏角像对的相对定向线元素具有厘米级精度。

综上，本节利用两组试验数据(不含与包含观测误差的像点坐标)，分别对不同焦距的小、中、大航偏角像对进行相对定向元素解算，结果表明本文方法正确可靠且可适用于大航偏角像对。

4 结 语

本文以像点坐标作为观测量，给其加入改正数，对共面方程进行线性化，推导了适用于不同焦距的连续像对相对定向元素解算公式，可得出结论如下：

(1) 该公式是对共面方程进行线性化而得，将像点坐标与相对定向元素同时作为模型中的未知量参与平差，其函数模型为附有参数的条件平差法。

(2) 当存在多于5对的同名像点时，可通过解算观测量及待求参数的改正数后，反复迭代，趋近最终解。该方法在相对定向元素的求导过程中，不存在小角近似简化，理论严密。

(3) 该公式可适用于解算不同焦距像对的相对定向元素，可处理不同相机拍摄的像片，提高现有影像信息的利用率，在一定程度上丰富了摄影测量理论。

[1] 张祖勋, 张剑清. 数字摄影测量学[M]. 武汉: 武汉大学出版社, 2014.

[2] 李德仁. 解析摄影测量学[M]. 北京: 测绘出版社, 1992.

[3] 张永军, 胡丙华, 张剑清. 基于多种同名特征的相对定向方法研究[J]. 测绘学报, 2011, 40(2): 194-199.

[4] 王琳, 张力, 艾海滨. 无人飞行器遥感影像的自动相对定向研究[J]. 测绘通报, 2011(11): 11-14.

[5] 王佩军, 徐亚明. 摄影测量学[M]. 武汉: 武汉大学出版社, 2013.

[6] MANSOUR F. Aerotriangulation by Coplanarity[J]. Journal of Engineering, 2006, 12(2): 247-258.

[7] 张剑清, 潘励, 王树根. 摄影测量学[M]. 武汉: 武汉大学出版社, 2014.

[8] 何海清, 程朋根, 王晋. 低空立体像对的严密相对定向[J]. 遥感信息, 2014, 29(6): 11-15.

[9] 张征宇, 朱龙, 黄叙辉, 等. 基于前方交会的5点相对定向[J]. 光学学报, 2015, 35(1): 231-238.

[10] 陆钰, 陈义, 郑波. 多基线近景摄影测量连续像对相对定向[J]. 同济大学学报(自然科学版), 2010, 38(3): 442-447.

[11] 赵军民, 魏新红, 张凯. 一种改进的相对定向标定方法研究[J]. 科学工程与技术, 2013, 13(32): 9744-9748.

[12] 唐健林, 龙盈, 董文浩, 等. 航空摄影测量面阵相机与线阵相机数据生产工艺的研究[J]. 测绘通报, 2015(S0): 48-51.

[13] 田雷, 马然. 无人机非量测相机检校方法研究[J]. 测绘通报, 2016(7): 81-83.

[14] 王新洲, 陶本藻. 高等测量平差[M]. 北京: 测绘出版社, 2006.

[15] 武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 武汉: 武汉大学出版社, 2015.

Strict Solution to Relative Orientation of Successive Photo Pair with Different Focal Lengths

LI Zhongmei,BIAN Shaofeng,JI Bing

(Department of Navigation, Naval University of Engineering, Wuhan 430033, China)

Aiming at the status that mostly available methods for relative orientation are used for stereo images with the same focal length, in order to make full use of image information photographed by different cameras, with image point coordinates under correction, coplanarity equation is strictly linearized by computer algebra system, and strict solution for relative orientation of image pair with different focal lengths is carried out. Finally, the correctness of the formulae is verified by numerical examples. This method could enrich theories of photogrammetry to some degree.

photogrammetry; stereo images; relative orientation; coplanarity equation; linearization

李忠美，边少锋，纪兵.不同焦距的连续像对相对定向严密公式[J].测绘通报，2017(4)：35-38.

10.13474/j.cnki.11-2246.2017.0115.

2016-09-20；

2017-01-17

国家自然科学基金(41631072；41604010；41471387)

李忠美(1990—)，女，博士生，主要研究方向为摄影测量理论算法。E-mail：15827116839@163.com

P23

A

0494-0911(2017)04-0035-04