对常用大地坐标系间坐标转换方法的评价

祁玉杰

(武汉大学测绘学院，湖北 武汉 430079)

对常用大地坐标系间坐标转换方法的评价

祁玉杰

(武汉大学测绘学院，湖北 武汉 430079)

常用坐标系间的相互转换对于现代工程应用有着十分重要的意义。实现坐标转换，需要若干公共已知点。然而，实际工程应用中，公共已知点的坐标信息一般难以获取，尤其是点的高程信息。针对该问题，本文利用实际数据，比较分析了在公共点无高程信息时，常用大地坐标系间坐标转换的4种方法(四参数法、多项式拟合法、高程迭代法、改化坐标法)在转换精度和其他方面的优劣。结果表明，4种方法都有着比较高的转换精度，而改化坐标法有着无需分带、单次迭代、仅需3个公共点、精度较高、精度指标一致的综合优势。

坐标转换；四参数法；高程迭代；多项式拟合；改化坐标

随着CGCS2000的启用，大量测绘成果将面临坐标转换至CGCS2000的问题[1-2]。如何实现坐标的高精度转换是个值得深入研究的课题。首先，由于技术手段的限制，我国此前建立的大地坐标系，如1954北京坐标系和1980西安坐标系等，存在着局部变形和系统累积误差，传统的坐标转换模型(如Bursa模型)难以消除这些误差，因而无法实现高精度的坐标转换。其次，1954北京坐标系为平面坐标系统，其高程信息通常是未知的，而且由于年代久远、资料丢失等因素，导致在实际工作中无法或极难获取公共点精确的大地高信息，即无法获得公共点在1954北京坐标系下精确的空间直角坐标，如果仍采用传统的Bursa模型实现坐标转换，其转换精度将受极大影响。

对此国内学者作了许多不同大地坐标系间坐标转化的研究工作[3-6]。成英燕等研究了适用于不同椭球的高斯平面坐标正反算的实用算法[7]，丁士俊等进行了几种不同坐标变换方法问题的研究[8]，成英燕等作了大尺度空间域下1980西安坐标系与WGS-84坐标系转换方法的研究[9]。实际工程应用中，公共已知点的高程信息一般难以获取。因此在坐标转化时需要用无高程信息的坐标转换方法，如四参数法、多项式拟合法、高程迭代法[10]、改化坐标法[11-14]等。各种坐标转化法在转换精度、计算效率等方面各有特点，而且在实际的坐标转换应用中，相邻的两个公共点可能分布在不同的投影带内，若进行分带处理，会导致不同带内的精度指标不一致。本文利用实际数据，计算比较分析四参数法、多项式拟合法、高程迭代法、改化坐标法4种坐标转化法的转换结果，得出改化坐标法相对其他3种坐标转化法有着无需分带、单次迭代、仅需3个公共点、精度较高、精度指标一致的综合优势。

1 几种常用的大地坐标系间坐标转换方法

1.1 四参数法

两个不同的大地坐标系平面坐标系之间转换时，可以采用四参数模型。在该模型中有4个未知参数：两个坐标平移量(Δx,Δy)，即两个平面坐标系的坐标原点之间的坐标差值；平面坐标轴的旋转角度α，通过旋转一个角度，可以使两个坐标系的坐标轴重合在一起；尺度因子k，即两个坐标系内的同一段直线的长度比值，实现尺度的比例转换，通常k值几乎等于1。

通常至少需要两个公共已知点，在两个不同大地坐标系中的4对x、y坐标值，才能推算出这4个未知参数，计算出了这4个参数，就可以通过四参数方程组，将一个平面直角坐标系下一个点的x、y坐标值转换为另一个平面直角坐标系下的x、y坐标值。

1.2 多项式拟合法

多项式拟合模型可以用来实现新旧坐标系之间大地坐标的转换，不需要公共点的高程信息，其中，采用最小二乘法来求取多项式拟合的系数。当多项式系数求解出来后，就可以使用该模型实现区域内任意一点的大地坐标在两坐标系之间的转换。一般二阶形式的多项式拟合模型方程为

(1)

式中，BΔ为新旧坐标系间纬度坐标增量；LΔ为新旧坐标系间经度坐标增量；a0、a1、…、a5为拟合纬度坐标增量BΔ的多项式系数；b0、b1、…、b5为拟合经度坐标增量LΔ的多项式系数；B=B1-B0，L=L1-L0，(B1,L1)为公共点在旧坐标系中的大地坐标，(B0,L0)为中心点在旧坐标系中的大地坐标，中心点可取公共点的平均位置。由于多项式拟合法在计算时有12个参数，故至少需要6个点才能进行计算。

1.3 高程迭代法

1.4 改化坐标法

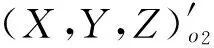
2 转换结果比较分析

本文取位于我国华中地区纬度跨度和经度跨度约为4°×7.5°内的165个公共点作为试验数据，数据中每10个公共点中选取一个公共点作为检核点，试验数据点位分布如图1所示。

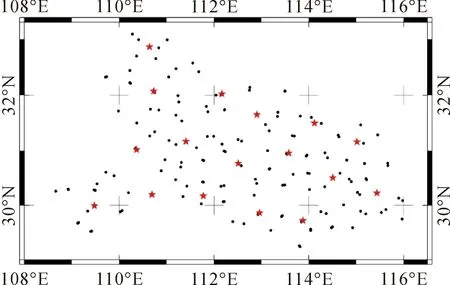
图1 试验数据点位分布(其中五角星点为检核点)

试验数据点分布在19、20带内，公共点具有1954北京坐标系和CGCS2000下的两套坐标，其中公共点在1954北京坐标系下的坐标为高斯平面坐标，无高程信息，在CGCS2000下的坐标为空间直角坐标。分别采用前文中介绍的4种坐标转换方法进行坐标转换，先计算坐标增量趋势值，然后进行加权残差拟合。采用不同方法计算的内符合精度和外符合精度结果见表1和表2。

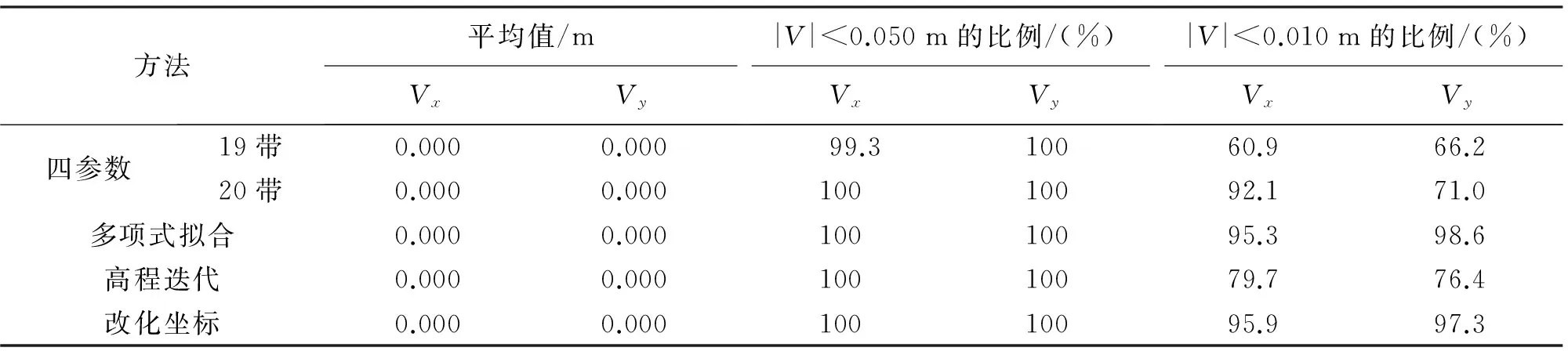
表1 采用不同方法计算的内符合精度

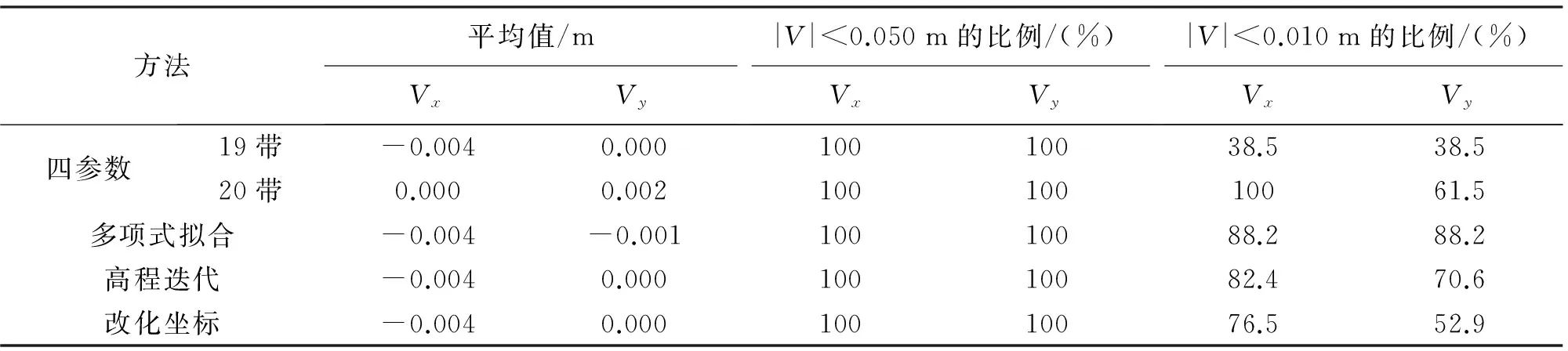
表2 采用不同方法计算的外符合精度

尽管公共点无1954北京坐标系下高程信息，4种方法仍可以实现待求点1954北京坐标系下的平面坐标与CGCS2000系下的平面坐标的转换，但是坐标转换的精度取决于待转换区域的大小及坐标转换方法的选择。其中采用四参数法在不同投影带内结果的精度区别较大，20带内点的残差小于0.010 m的比例大于19带内的比例，这是由于试验数据大部分处于19带内，20带的公共点所占范围较少导致的。残差的平均值均小于0.004 m，残差绝大部分小于0.050 m。

表2中4种方法的残差全部小于0.050 m，而表1中4种方法的残差绝大部分小于0.050 m，这是由于检核点的数目较少，小样本不足以完全反映整个试验区域。由表1中的残差小于0.010 m的比例可知，多项式拟合法和改化坐标法的内符合精度比四参数法和高程迭代法的内符合精度高，并且多项式拟合法和改化坐标法的内符合精度在同一级别。而由表2中的残差小于0.010 m的比例可知，多项式拟合法的外符合精度最高，四参数法在19度带内的外符合精度最低，改化坐标的外符合精度比较高。对比表1、表2中的残差小于0.010 m的比例可知，四参数法和改化坐标法的残差比例变化较大，这可能与两种方法采用的模型有关，也有可能是由于检核点的数目较少和检核点的位置选取所导致。四参数法是4个参数的布尔莎模型，而改化坐标法中采用了七参数的布尔莎模型，这种旋转加平移的模型可能导致坐标转换后内、外符合精度变化较大。

图2、图3分别列出了内、外符合结果的残差标准差和残差模最大值。由图2可知，多项式拟合法和改化坐标法的残差标准差相同，x轴方向都为0.004 m，y轴方向都为0.003 m，并且相对于四参数法和高程迭代法，残差模最大值也比较小。再次说明了多项式拟合法和改化坐标法的内符合精度高。由图3可知，四参数法20带内的标准差在x轴方向都为0.003 m，y轴方向都为0.009 m，多项式拟合法为0.009和0.008 m，改化坐标法和高程迭代法为0.012和0.011 m。再结合4种转换方法残差模的最大值的数据可知，四参数法在20带内的外符合精度最好，其次为多项式拟合法、改化坐标法、高程迭代法，最后为四参数法在19带内的精度。

3 结 语

本文利用实际数据，比较分析了在公共点无高程信息时，实现不同的大地坐标系间坐标转换的4种方法：四参数法、多项式拟合法、高程迭代法、坐标改化法在转换精度和其他方面的优劣。从数据统计结果可以看出，四参数法、多项式拟合法、高程迭代法和改化坐标法可以用于一般精度要求的坐标转换，对于4°×7.5°的大区域，转换精度优于5 cm。其中用四参数法进行坐标转化时需要分带处理，在同一带内的点坐标转化精度一致，不同带内的点坐标转化精度不一致，并且四参数法对于小区域的计算精度明显高于对大区域的计算精度；多项式拟合法有着较高的转化精度，转化时至少需要6个公共点；高程迭代法需要多次迭代才能尽可能地提高精度。而改化坐标法相对其他3种坐标转化法有着无需分带、单次迭代、仅需3个公共点、精度较高、精度指标一致的综合优势。

图2 内符合残差标准差和残差模最大值

[1] 陈俊勇.我国建立现代大地基准的思考[J].武汉大学学报(信息科学版)，2002，27(5):441-444.

[2] 魏子卿.我国大地坐标系的换代问题[J].武汉大学学报(信息科学版)，2003，28(2):138-143.

[3] 张训虎，刘晋虎，何川，等.2000国家大地坐标系转换常见问题分析[J].测绘通报，2016(9):52-55.

[4] 吕志平，魏子卿，李军，等.CGCS2000高精度坐标转换格网模型的建立[J].测绘学报，2013，42(6):791-797.

[5] 方兴，曾文宪，刘经南，等.三维坐标转换的通用整体最小二乘算法[J].测绘学报，2014，43(11):1139-1143.

[6] 李博峰，黄善琪.大角度三维基准转换的解析封闭解[J]. 测绘学报, 2016， 45(3):267-273.

[7] 成英燕，李夕银.适用于不用椭球的高斯平面坐标正反算的实用算法[J].测绘科学，2004，29(4):26-27.

[8] 丁士俊，张忠明.几种不同坐标变换方法问题的研究[J].四川测绘，2005，28(1):16-19.

[9] 成英燕，程鹏飞，秘金钟，等.大尺度空间域下1980西安坐标系与WGS-84坐标系转换方法研究[J].测绘通报，2007(12):5-8.

[10] 谢鸣宇,姚宜斌.三维空间与二维空间七参数转换参数求解新方法[J].大地测量与地球动力学，2008，28(2):104-109.

[11] 张卡，张道俊，盛业华，等.三维坐标转换的两种方法及其比较研究[J].数学的实践与认识，2008，38(23):121-128.

[12] 孔祥元，郭际明，刘宗泉.大地测量学基础[M].2版.武汉:武汉大学出版社，2010.

[13] 赵文，刘邢巍，袁鹏.格网节点坐标初值对格网坐标转换精度的影响[J].测绘地理信息，2015，40(2):39-43.

[14] 赵文，刘邢巍，袁鹏.七参数坐标转换中一种削弱高程误差影响的新方法[J].测绘通报，2016(1):11-14.

[15] 金俭俭，董彦锋，王茹，等.GPS控制网坐标转换模型的研究[J].测绘通报，2015(S1):81-83.

Evaluation of Coordinate Transformation Methods between Common Geodetic Coordinate Systems

QI Yujie

(School of Geodesy and Geomatics, Wuhan University, Wuhan 430079,China)

The transformation between different coordinate systems is of great significance to modern engineering applications. Several common known points are needed before the transformation. However, it is difficult to obtain the coordinate information, especially the elevation information, of common known points in practical engineering applications. Aiming at this problem, four methods (four parameters method, polynomial-fitting method, height substitution circular method, transform-coordinate method) are compared and analyzed in transformation accuracy and other aspects. The data used is actual and has no elevation information. The results show that all the methods have high conversion accuracy. And the transform-coordinate method has the advantages of no zoning, only one iteration, only 3 common points, high precision and consistent accuracy index.

coordinate transformation; four parameter method; height substitution circular; polynomial-fitting; transform-coordinate

祁玉杰.对常用大地坐标系间坐标转换方法的评价[J].测绘通报，2017(4)：13-16.

10.13474/j.cnki.11-2246.2017.0110.

2016-08-18;

2017-01-29

国家杰出青年科学基金(41525014)

祁玉杰(1991—)，男，硕士生，主要从事GNSS数据精密处理研究。E-mail: yjqi@whu.edu.cn

P207

A

0494-0911(2017)04-0013-04