数学实验:数学“创客教育”的课程载体

摘要:作为数学“创客教育”的课程载体,数学实验有着自身的特质——思想与实践对接、归纳与演绎圆融、思维与创造共生。运用“创客教育”理念进行数学实验,要警惕“讲解”对“操作”的代替、“结果”对“过程”的僭越、“操作”对“思想”的轻视。在引领儿童进行“数学众创”过程中,必须引发儿童的“主动之意”,彰显儿童的“理解之美”,呈现儿童的“解放之乐”,实现儿童的“成长之需”,由此开辟崭新的儿童数学“众创路径”。
关键词:数学实验;创客教育;课程载体
中图分类号:G623.5 文献标志码:A 文章编号:1673-9094(2017)04A-0069-04
基于互联网时代“大数据”、“云计算”背景,以创新为灵魂的“创客教育”必须扎根学校课堂。作为数学“创客教育”的课程载体,数学实验能够有效统合课程资源,实现跨学科、跨领域的知识融合、技能整合。在数学实验过程中,儿童摆脱“离身思维”,“手脑”结合、“做思”共生,形成一种“具身认知”。[1]数学实验将成为开启数学“创客教育”的新动力引擎。
一、创客教育:诉求数学实验的“课程价值”
现代数学观认为,数学不是无可怀疑的“真理集合”,而是动态、可误的,是一个不断地猜想、尝试、计算、推理、证实或证伪的动态生长过程。正是在这个意义上,著名数学教育家波利亚说,“数学有两个侧面:一方面是欧几里得式的严谨科学,从这方面看,数学像是一门系统的演绎科学;但另一方面,创造过程中的数学,看起来却像一门实验性的归纳科学。”在数学“创客教育”过程中,数学实验有着独特的课程价值。
(一)思想与实践对接
所谓数学实验,是指儿童在数学学习过程中所产生的操作性、印象性或符号性的实验或准实验(虚拟实验),它超越了纯粹的“纸笔数学”,让儿童的数学思想与数学实践无缝对接、有效整合。教学《三角形三边关系》,笔者首先向学生们提供一根小棒(15厘米),让学生测量,然后让他们自主创造“结构性素材”——将小棒分成三段尝试围,在围的实验过程中展开自我追问:为什么有的能围成,而有的却围不成?思维的触角延伸至“三角形三边的数据关系”。最后笔者让学生们将“围成”和“围不成”的实验数据用表格分类整理,产生对“三角形三边关系”的理性认识。在此,数学实验引领儿童数学思维,数学思维修正儿童的数学实验。[2]
(二)归纳与演绎圆融
数学实验开辟了儿童“用手思考问题”的道路,儿童正是在“动手做”的过程中解压了数学思维。同时,数学思维反过来对数学实验经验进行必要的凝聚——抽象和概括。这是一个伴随儿童认知冲突、矛盾解决的不断猜想、探究、尝试与论证的过程。教学《两位数除以一位数》,笔者首先出示63÷3,学生用手中的小棒实验,有的先分个位上的3根,有的先分十位上的6捆;然后笔者出示76÷2,学生依然是两种分法,但已经开始通过自我“内部言语”归纳出“先分十位”更合理、更方便些;接着笔者出示42÷3,这时个位上的2不够分,学生只能从高位开始。在学生通过实验理解了算理后,笔者让他们进行竖式计算,演绎生成出“两位数除以一位数”的算法模型[3]。从“工具操作”到“表象归纳”再到“符号演绎”,儿童的实践经验升华为数学的理性认知。
(三)思维与创造共生
数学实验是孕育儿童数学创造的孵化器,儿童的一个个“小微创”在数学实验中诞生。在“微创”过程中,儿童主动观察、思维、想象、推理,主动画图、剪拼、测量,等等。教学综合实践活动——《神奇的“莫比乌斯圈”》,笔者首先让学生观察、触摸,他们迅速感知到:“莫比乌斯圈”只有一个面、一条边。然后,笔者让学生用剪刀沿“莫比乌斯圈”中线剪开,他们惊奇地发现:剪后的“莫比乌斯圈”变成一个大纸环。接着,笔者让学生展开实验,于是有学生剪了“莫比乌斯圈”的三分之一,有学生先剪二分之一,再剪二分之一等。在看、剪的过程中,他们萌发出创造性想象:老师,如果把磁带做成莫比乌斯圈,就不用翻面了;老师,如果把“输送带”做成莫比乌斯圈,或许能延长使用寿命呢……学生们激情飞扬,创意迭出。最后,笔者用迷人的“莫比乌斯建筑”、“莫比乌斯凉鞋”等激活儿童创想、创行。
二、创客教育:观照数学实验的“问题现象”
在数学实验过程中,儿童的抽象思维与形象思维并存,感性观察与理性分析交织。唯有如此,数学学习才能激活儿童的“群智群力”,激发儿童的研究与探索。然而,当我们运用“创客教育”理念观照当下数学实验时,却发现存在诸多问题——“数学讲解”对“實验操作”的代替、“数学结果”对“实验过程”的僭越、“实验操作”对“数学思想”的轻视等。
(一)“数学讲解”对“实验操作”的代替
数学实验是实施数学“创客教育”的价值载体。实践中,笔者发现许多数学实验蜻蜓点水、一带而过,甚至将丰富生动的“做实验”减缩为“说实验”“讲实验”“演实验”。教学《可能性》,有教师为节约课堂教学时间,将他们自认为枯燥、繁琐的摸球实验简化或悬置,代之以数学讲解,让学生们猜测“摸球结果”,直接出示数学家研究“等可能性”的“抛硬币”实验数据。如此,儿童体验不到事件的随机性,更谈不上掌握统计方法、感悟概率思想。
(二)“数学结果”对“实验过程”的僭越
教学中,有教师为追求实验结果一步到位,甚至为求实验顺畅而对实验过程进行前置告知、过渡预设,导致儿童操作简单、思维肤浅。教学《圆的周长》,一位教师首先出示圆周率近似数——3.14,接着让学生实验验证。于是有学生用“绕线法”测量圆周长,有学生用“滚圆法”测量圆周长。通过计算圆周长和直径的商,学生发现不是3.14,他们为迎合教师纷纷篡改、杜撰实验数据,甚至悬置数学实验,代之以数学计算。充满童趣的探究实验被教师误导为验证实验,而教师对儿童实验过程又缺乏具体、明确的指导,导致儿童伪造实验数据。
(三)“实验操作”对“数学思想”的轻视
在创客教育中,“实验”是“数学”的载体,“思想”是“数学”的灵魂,要警惕儿童沦落为机械的“操作工”。必须导引儿童展开深度的数学思考,让儿童感悟、体验、应用数学。例如“间隔排列”问题是数学经典问题,有教师教学时只是蜻蜓点水地让学生“摆学具—观察特征”“猜想—验证”。整个过程没有“对应学具”的分组操作,没有让学生慢慢感悟“对应思想”,导致学生一头雾水,始终不能深刻理解“为什么‘两端物体相同,‘两端物体比‘中间物体多1”,在应用时学生不知所措,加1、减1还是相等呢?
三、创客教育:探寻数学实验的“众创路径”
作为体验式学习,数学实验是儿童在“做中学”、“做中玩”、“做中研”、“做中创”。实验过程中,教师成长为创客导师,营建创想氛围、打造创想空间、激发儿童创想意识,对儿童的实验创新进行“众扶”、“众筹”,让儿童想创、敢创、能创。
(一)从“约”到“放”,通过“对比实验”引发儿童“主动之意”
在数学实验过程中,要引发儿童主动学习的愿望,让儿童自主建构。教学《圆锥的体积》,许多教师实验时直接出示“结构性素材”——“等底等高的圆柱圆锥”,这是教师胁迫下儿童的“被实验”,为什么非得选择圆柱且是“等底等高”的圆柱?[4]笔者教学时由“约”而“放”,首先出示大小、形状不同的立体模型(如长方体、正方体、圆柱体、三棱柱等)让学生自主选择。学生们纷纷选择圆柱。
师:你们为什么选择圆柱?
生1:因为圆柱和圆锥的底面都是圆形,便于比较。
师:这里有四种规格的圆柱圆锥(“等底不等高”1组、“等高不等底”1组、“等底等高”2组、“不等底不等高”2组),你们选择哪种规格?
生2:我选择“等底等高”的圆柱圆锥,这样更便于比较。
接着笔者让学生用四种规格的圆柱圆锥(装沙子、水)分组进行对比实验。学生们惊奇地发现有三组实验结果是“圆柱的体积大约是圆锥体积的三倍”,其中两组是“等底等高”,一组是“不等底不等高”。接着笔者组织学生讨论,讨论中,他们认识到,由于沙子之间有空隙,所以用水做实验更科学,并且深刻地感悟到,等底等高的圆柱圆锥,圆柱的体积一定是圆锥的3倍,而圆柱的体积是圆锥的3倍,它们可能“等底等高”,也可能“不等底不等高”。他们还用“高瘦瘦和矮胖胖”生动地解释“不等底不等高”的实验结果。这里,儿童充分发挥自我数学实验的能动性,真正经历了“圆锥体积公式”诞生历程,成为数学意义上的“创客”。
(二)从“迷”到“思”,通过“模型实验”彰显儿童“理解之美”
儿童在生活、数学学习中会产生许多“迷思概念”(一种错误概念或思维结构),教学中教师可以运用数学实验点化儿童思维,让儿童思维澄明、敞亮。
六年级试卷有这样一道选择题:一个真分数,如果分子和分母同时加上k(k>0),所得分数()(>、<、=)原分数。许多学生看到“同时加上k”,所以选择了“现分数=原分数”。
对于儿童的“迷思”,笔者没有如一般教师运用“假设法”(即举几个例子让学生尝试运算),而是做了一个可视性的“模型实验”[5]。
师:老师这儿有一杯糖水,它的糖占糖水 ,如果老师再加入k克糖,糖、糖水、含糖率分别发生了怎样的变化?
生1:糖多了,糖水也多了。
生2:变甜了。
师:变甜了就是什么变化了?
生3:含糖率升高了。
师:现在你知道一个分数的分子和分母同时加上同一个大于0数,分数变大的道理了吗?
学生们恍然大悟,原来一个抽象的“不等式问题”竟然可以用一个“糖水浓度”实验来解释,既直观形象又严密深刻!这里,儿童感受到数学的美妙与神奇。
(三)从“低”到“高”,通过“模拟实验”呈现儿童的“解放之趣”
数学实验过程应该成为儿童感受数学力量的过程,充分彰显儿童的解放旨趣。从本质直观到理性判断,儿童能够感受自我的本质力量!教学《长方形和正方形面积》,笔者让学生们做“贴瓷砖”的模拟实验。
教师首先给出一个小长方形纸(长、宽均为整厘米数),让学生用“1平方厘米”的小正方形塑料片进行拼摆,通过数,儿童直观感知到长方形纸的面积;然后出示一个大长方形纸,先让学生估计长方形纸的面积,再让他们用直尺分别量出长方形纸的长、宽,接着再让他们用“1平方厘米”的小正方形塑料片拼摆。学生发现,塑料片不够拼摆了。
师:不够拼摆怎么办呢?
生1:可以用笔画出空出的部分,然后数一数。
生2:可以先用小正方形塑料片摆一行,然后画一条横线,再沿着这条横线向上对折。(简化思想初现端倪)
生3:可以在头脑中想象。
师:非得画满、折满么?有没有更为简单的方法?(沉默片刻)
生4(兴奋地):只要用小正方形摆在长方形纸的长边和宽边上,然后再用“长边上的个数”乘“宽边上的个数”。
生5:长方形纸的长边长度就是长边上的小正方形的个数,宽边长度就是宽边上的小正方形的个数,所以我们只要知道长方形纸的长和宽,就能算出长方形纸的面积。
至此,“长方形的面积公式”自然诞生了。教师故意设置“短斤缺两”的工具,让儿童超越实验的工具理性,经由自我的实践理性,迈向数学的解放理性。
(四)从“外”到“内”,通过“切片实验”实现儿童的“成长之需”
作为数学“创客教育”的課程载体,数学实验能够让儿童外显的实践操作与内隐的数学思维有机融合,让活动成为外化的思维,让思维成为内化的活动。正是在这个意义上,用手思考也可以理解为用头脑做、用头脑看、用头脑听……例如对于这样的习题:
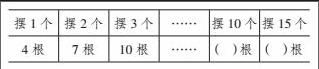
小英像图这样摆正方形,摆1个用4根小棒,摆2个用7根小棒,摆3个需要()根小棒,摆10个呢?摆15个呢?100根小棒能摆多少个正方形?
教学时,笔者让学生做“切片实验”[6],即用火柴棒摆前几个图形探究,以小见大找规律。操作中,笔者适度介入,给操作注入思维,摆1个正方形需要几根火柴棒?摆2个正方形需要增加几根火柴棒?上下看,增加几根?左右看,增加几根……学生们将操作结果用表格进行整理,形成“实验切片”。
当学生们操作到第3个正方形时,笔者引导他们观察,将实验结果用算式进行记录,于是产生了多样化的数学表达:
生1:4;4+3;4+3×2;……
生2:1+3;1+2×3;1+3×3;……
生3:2+2;4+3;6+4;……
生4:1×2+2×1;1×3+2×2;1×4+2×3;1×5+2×4;……
…………
师:还需要接着摆下去吗?
生:不用了,我们找到了规律。
在摆小棒过程中,儿童始终关注着各自视界里的规律。这些规律的探寻过程是儿童将自我外在的操作实验内化成自我的思想实验。他们在头脑里操作,在头脑中“下盲棋”,经过自我推理、计算,建构出各自的数学规律,其核心素养得到了提升。
数学实验是一种打通教材文本和儿童知识经验、学习心理等的主客交融的综合性学习。在这种整体性学习中,儿童主动观察、思考、操作、发现。数学实验为数学理解提供了外源帮助,数学理解为数学实验提供了内源支撑。在数学实验过程中,儿童从依赖操作实验的工具性理解走向超越操作的关系性理解、创新性理解,进而实现自我的思维跃迁,数学实验室也成为儿童的“创想空间站”、“数学创客坊”。
参考文献:
[1]叶浩生.身体与学习:具身认知及其对传统教育观的挑战[J].教育研究,2015(4).
[2]武建军.数学实验:小学生实践操作与数学思维的视界融合[J].江苏教育(小学教学),2015(1).
[3]刘正松.数学实验:推开数学学习的另一扇窗[J].教育研究与评论(小学教育教学),2015(8).
[4]陈蕾.以“圆锥的体积”为例谈小学数学实验的教学[J].江苏教育(小学教学),2009(6).
[5]储冬生.数学实验:小学生实践操作与数学思维的视界融合[J].教育研究与评论(小学教育教学),2011(12).
[6]孙朝仁.朱桂凤.初中数学“实验切片”衔接教学的实践与思考[J].江苏教育研究(实践版).2015(6).
责任编辑:石萍
收稿日期:2016-10-28
作者簡介:汪树林,如皋市东陈镇丁北小学(江苏如皋,226571)教科室主任,南通市骨干教师,研究方向为儿童数学教与学。

