7～9年级学生概率比较的策略及其发展

何声清，巩子坤



7～9年级学生概率比较的策略及其发展

何声清1，巩子坤2

（1．北京师范大学教育学部，北京 100875；2．杭州师范大学理学院，浙江杭州 310036）

以204名7~9年级学生为被试考察概率比较的策略及其发展．结果表明，7~9年级学生在概率比较任务中主要表现出两种正确策略和5种朴素策略．其中，正确策略如“基于精确的样本空间”的使用频率随年级逐级递增；朴素策略如“认为概率无法预测和量化”、“基于数量或比例关系”、“第I类等可能性偏见”等的使用频率随年级逐级减少，而“基于模糊的样本空间”、“第II类等可能性偏见”等的使用频率随年级不降反升．对教学的建议有：针对性地消除学生的错误策略；加强学生对于古典概率“理论先验性”和“可度量性”的理解；通过直观图示发展学生对复杂事件概率的理解．

7~9年级学生；概率比较；策略；发展

1 研究缘起

概率素养（probability literacy）[1]是当今世界公民必备的数学素养，人们需要在纷繁的信息世界里辨识随机现象，并对不确定性事件进行概率比较（probability comparison）以作出合理推断．在课程方面，概率内容自20世纪末开始相继进入各国中小学课程标准（如，AEC[2]，NCTM[3]）．中国2001年颁布的《全日制义务教育数学课程标准（实验稿）》（以下简称《课程标准（实验稿）》[4]也第一次将其纳入义务教育数学课程．2011年颁布的《义务教育数学课程标准（2011年版）》（以下简称《课程标准（2011年版）》[5]进一步对其难度和要求进行调整，在第三学段才要求进行概率比较．在教材方面，以人民教育出版社教材[6]（以下简称人教社教材）为例，该教材在九年级上册设置了概率比较的内容，即“用列举法求概率”．以古典概型为例，概率比较是建立在演绎推理之上的，决策者从理论上即可构造随机试验的所有可能结果进而计算事件的概率，因而它具有先验性．在教学方面，作为义务教育阶段数学课程新近引入的内容，它一方面对教师的概率知识提出了一定的挑战，“许多教师在其自身基础教育阶段的数学课程中都尚未学习概率知识”[7]；另一方面，它对教师“关于学生概率认知的知识”提出了较高的要求，教师不仅要明晰概率内容在数学课程中的定位，还要关注学生是如何学习和理解概率的[8]．研究者曾对5~8年级（11~14岁）学生概率比较的水平进行了初步研究[9]，结果表明，5~8年级学生概率比较的水平先后经历了缓慢发展、倒退发展及停滞发展3个阶段，学生在较复杂的问题情境中（如“摸出2个球”）遇到了困难．然而，一个尚待解决的问题是：学生在这些问题情境中为什么遇到了困难？他们是如何进行概率比较的？有哪些典型的朴素策略？这些策略是如何发展的？这里将对以上问题进行考察，为概率内容的课程及教学设计提供参考．

2 研究设计

2.1 研究对象

研究以北京市某学校7-9年级的204名学生（7年级69人，8年级74人，9年级61人）为被试，其中男性被试113人，女性被试91人．所有被试采用四位数（即，ABCD）进行编码．A表示年级（7、8、9）、B表示性别（1代表男性，2代表女性）、CD表示被试的序号．例如9113号，表示该被试是9年级男性13号被试．

2.2 研究材料

测试材料共设计了5个“球—盒模型”概率比较的题目．“球—盒模型”在考察中小学生概率认识方面有诸多优点：一方面摸球游戏对于儿童而言是比较熟悉的，另一方面摸球模型可以避免日常模型（如，下雨、阴天）的不规范．在“球—盒模型”中，常常按照“摸出球的个数”区分出“摸出1个球”和“摸出2个（或多个）球”等问题情境．研究[9]表明，学生在“摸出1个球”的问题情境中往往有较好的表现，而在“摸出2个球”的问题情境中则遇到了困难．据此，该研究的测试仅考虑“摸出2个球”的问题情境．各题目按照“球的颜色种类”、“球的总数”及“盒子个数”等变量设置情境．测试题目的结构如表1所示．

2.3 研究方法

研究采用问卷调查和访谈相结合的方法．研究者在问卷中不仅要求被试对事件的概率进行比较，还要求其详细写出理由．在访谈环节，选取了持典型策略的被试进行深入交流，详细了解概率比较时的思维过程．

每个题目的T1按照0、1两级计分，正确记1分，错误记0分；关于T2的编码，研究者首先对被试的理由进行定性分析，概括出典型的策略类型，然后对不同策略按类别进行编码．

以Cronbach系数为指标，对各题目T1的内部一致性进行了分析．结果表明，该问卷具有较高的同质性信度（=0.812）．

3 结果与分析

3.1 7~9年级学生概率比较的策略类型及其分布

儿童在概率比较任务中共表现出7种主要的策略（该7种策略是学生作答中典型的或者频率较高的策略．除此之外，尚有16.27%的其它作答（如，基于主观猜测、无关或空白作答，等）在此未作讨论）．其中正确策略两种，朴素策略5种．对T1的得分率和T2的正确策略率进行了对比（表2）．结果表明，各年级学生在各道题目上的T1得分率均明显高于T2的正确策略使用频率．换言之，7~9年级学生在概率比较任务中正确策略的使用频率不高（仅20.98%），然而尽管如此，学生的得分率均值（40.1%）却高于正确策略的使用频率近一倍．这说明，即使学生尚未发展正确的概率比较策略，他们也能做出正确判断．这直观地说明，在所有能作出T1正确结果的学生中，有一半是基于其它策略（朴素策略甚至错误策略）进行判断的．具体数据见表2．

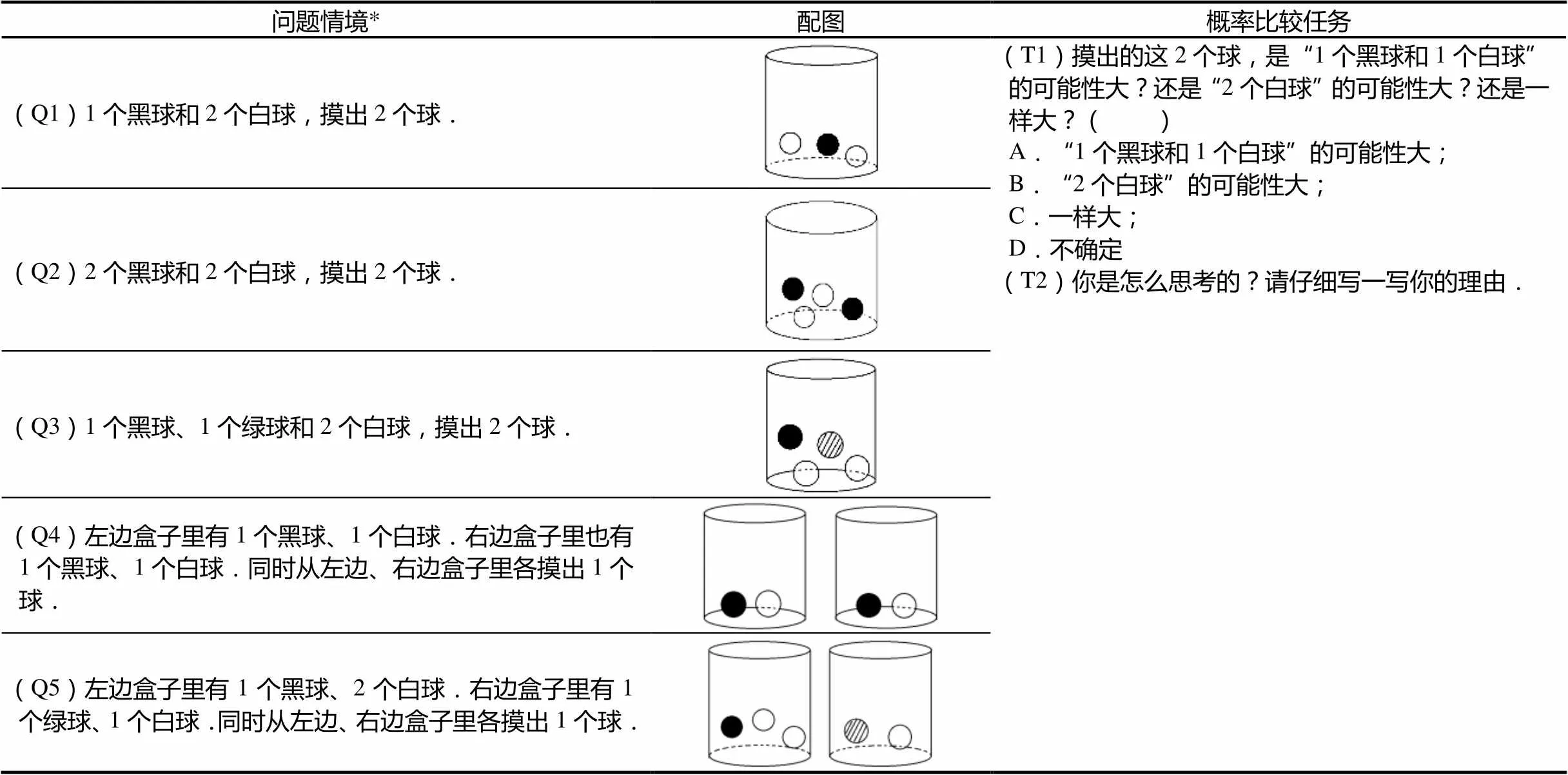
表1 测试题目的结构

注：各题目题干均是“1个（2个）不透明的盒子里（分别）有×个白球、×个黑球和（和×个绿球），它们除颜色外都相同．闭上眼睛，摇一摇盒子后，从盒子里摸出2个球（各摸出1个球）．

表2 被试T1任务得分率与T2任务正确策略使用频率（%）的对比

为了证实这一点，该研究以两种正确策略为预测因子对学生“概率比较”得分进行回归分析．两因子的共线性系数值为0.981，值为1.019，表明推翻共线性假设，二者适合作为独立预测因子．在模型汇总（表3）中，调整后的2（57%）与样本报告的2（57.4%）差别不大，说明样本和总体的拟合较好，模型能够解释57%的变异．(2, 201)=135.675（＜0.001），表明模型可接受．

表3 模型汇总b

注：a. 预测变量：（常量），分步试验法，基于精确的样本空间策略；b. 因变量：“概率比较”得分水平

以上分析表明，学生T1的得分率均值较低（40.1%），在这些能够正确作答的学生中，仅一半学生使用了正确的策略．换言之，如果把“是否采用了正确的策略”作为“学生概率比较能力”的判断标准，近80%的7~9年级学生尚未发展正确的策略．需要指出的是，9年级被试尚未学习（在进行该测试时，被试尚未学习到“概率初步”章节）“用列举法求概率”，该年级学生正确策略的使用频率也不高．

（1）正确的策略．

基于精确的样本空间（17.87%），是指构造试验的所有可能结果构成的集合，并据此计算事件的概率．对于古典概型而言，样本空间是概率比较的前提：在一次试验中，如果可能出现的结果只有有限个，且各种结果出现的可能性大小相等，试验的所有可能结果的个数叫做样本空间（记为），事件A包含的可能结果个数记为，则事件A发生的概率(A)=/．在古典概型（如“球—盒模型”）中，各事件的概率是可以通过理论计算的，因而它具有先验性，包含了一定的推理成分．因此，基于样本空间策略代表了学生思维的较高层次．以Q2为例，被试8209认为“1个黑球和1个白球”的可能性大，因为“1个黑球和1个白球占的可能性为2/3，2个白球的可能性为1/6，2/3比1/6大，1个黑球和1个白球的可能性就大”．

分步试验法（3.11%），是指用“慢动作”设想摸球的过程，把事件分解为一系列子事件加以模拟．在不放回试验中（如该研究中的Q1~Q5），把“同时摸出2个球”分解为“先摸出1个球，再摸出1个球”，对于结果的判断没有影响．事实上，将“同时摸球”分解为“先后摸球”更易于学生理解．因为在组合运算中，尽管它对“组合的结果”的顺序不作要求，但是按照一个逻辑清晰的顺序进行组合会避免重复或遗漏的情况，进而能够准确列举试验的所有可能结果．以Q2为例，被试8113（如图1）认为“1个黑球和1个白球”的可能性大，“因为先摸出1个球，如果是白球，则摸到另1个白球的可能性占1/3，黑球的可能性为2/3；如果是黑球，摸到白球的可能性占2/3．综合分析，摸出‘1个黑球和1个白球’的可能性大”．

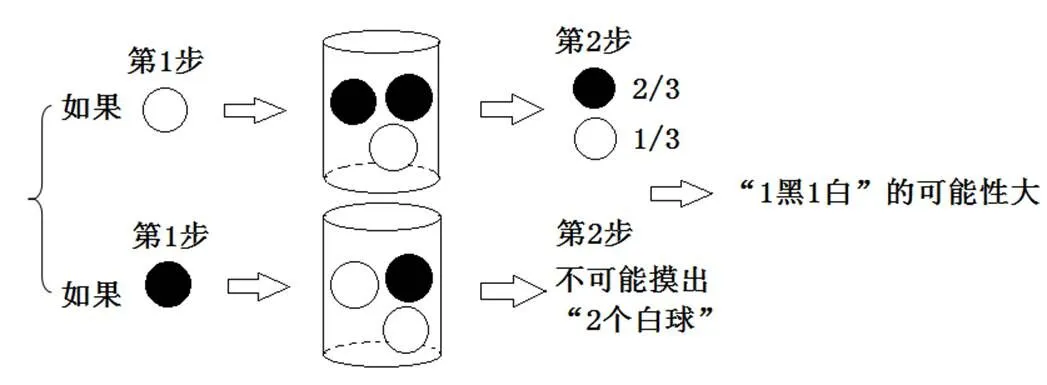
图1 “分步试验法”思维过程模拟

在该题中，“分步试验法”不仅具有合理性，也符合学生的思维水平．在访谈中，对被试8113的回答提出了追问：“题目要求的是‘同时’摸出2个球，你这样是分开摸的，不是吗？”被试8113解释道：“我把手伸进去一个一个地摸球，拿出来的时候我同时拿出来就好了．”

需要指出的是，儿童的策略常常是不稳定的．例如，被试8226认为，“有可能第一次摸到白的，第二次就摸到黑的，因为黑的比白的几率多，但不排除会摸到白球的可能；如果第一次摸到黑的，第二次白比黑几率多，但也不排除摸到黑球的可能．”该被试尽管对“摸出2个球”的动作进行了分解，在“摸出第1个球”时也进行了分类讨论，然而在最终决策时遇到了困难：她没有意识到，如果第一次摸出的是白球，第二次摸出黑球的理论概率比摸出白球的大；同理，如果第一次摸出的是黑球，第二次摸出白球的理论概率比摸出黑球大．这表明，儿童尽管具备了朴素的理论概率思维，然而其不良的直觉干扰了其概率决策．

（2）朴素的策略．

等可能性偏见[10]（22.98%），是指把“所有结果都有可能发生”泛化理解为“所有结果的发生都是有可能的，并且发生的可能性相等”．进一步，有研究[11]把该策略划分为两种具体的表现形式．这在该研究中也得到了证实，为了讨论方便，把这两种形式称为第I类等可能性偏见和第II类等可能性偏见．前者认为所有事件的可能性大小是“相等的”且均为50%；后者也认为事件的所有可能性大小是“相等的”且均为1/（是指其列举的所有可能结果个数）．

以Q2为例，被试7123认为“1个黑球和1个白球”与“2个白球”的可能性一样大，因为“摸出1个黑球和1个白球是50%，摸出两个白球也是50%”．被试9102也认为二种情况的可能性一样大，但给出了不同的解释，“因为有3种可能，因此‘1个黑球和1个白球’和‘2个白球’的可能性一样大，1/3=1/3”．不难发现，前者是第I类等可能性偏见，后者是第II类等可能性偏见．进一步发现，7~9年级学生第I类等可能性偏见和第II类等可能性偏见的使用频率分别为13.29%和9.69%．这表明，持有第I类等可能性偏见的学生比例要比持有第II类等可能性偏见的学生比例更高．

基于数量或比例关系（20.77%），是指依据球的数量、比例（比率）判断概率大小及比较概率．以Q2为例，被试7109认为“1个黑球和1个白球”与“2个白球”的可能性一样大，“因为盒子里装的白球和黑球的数量均匀”．

需要指出的是，在“摸出1个球”试验中，基于数量或比例关系基本可视为一种较规范的策略．因为所有的可能结果数恰好是球的总个数，抽取的样本即是“1”，不需要进行组合运算．然而，对于“摸出2个球”试验，这显然是一种错误的策略．因为决策者需要进行组合运算，样本的形态也变成一个“组合”，仅仅从单一的球的个数去解释事件的概率是没有理解“样本”的表现．

认为概率无法预测和量化[12]（8.57%），认为概率是不可预测和比较的．以Q2为例，被试7130无法对事件的概率大小做出判断，因为“都有可能但不能准确确定．”被试7229则认为：“人类目前还没有可以预知未来的能力，所以我不确定．”

基于模糊的样本空间[9]（5.6%），是指将外部特征相同的样本合并为一种情况，该策略具体表现为两种形式．为了讨论方便，将其区分为第I类模糊的样本空间和第II类模糊的样本空间．以Q2为例，被试9132认为“1个黑球和1个白球”与“2个白球”的概率一样大，“因为只有3种可能，黑白、白白、黑黑”（第I类模糊的样本空间）．被试7241则认为“1个黑球和1个白球”的概率大，“因为1黑1白有黑白、白黑两种可能，白白是有1种可能”（第II类模糊的样本空间）．需要指出的是，尽管后者能够使被试在概率比较时做出正确判断，但这种策略和前者一样，均没有穷尽事件的所有可能结果，因此不是正确的策略．

局部的分步试验法（4.66%），是指在列举事件的“组合结果”时表现出了“分步”的思想，但没有穷尽所有可能的结果．实际上，在“分步”过程中，“第1步”之前的工作是“分类”，即第1步本身有多种可能性．而学生常常忽略了第1步结果的多种可能性．该策略的局限在于，它对于概率比较任务“时灵时不灵”，取决于其“第1步”的假设．以Q2为例，被试8232认为“1个黑球和1个白球”的概率大，“因为肯定要摸1个白球，所以把它排除了．就剩下两个黑球1个白球，摸到黑球的几率是2/3，白球是1/3．1/3＜2/3，所以摸1个黑球和1个白球的可能性大．”实际上，该被试对Q2的题意进行了如下转化：既然“白球”在上述两种情况中都有，因此把白球“固定”（第一步先想象摸出白球），接下来只需判断第2步是黑球的概率大还是白球的概率大．然而，这种转化忽略了“第1步是黑球”的可能性，它并不是一直有效．该被试在Q1作答中的类似理由就显得苍白无力，“我认为二者的可能性一样大，因为一共3个球，肯定要拿到一个白球，那就把它排除掉，就剩下1白1黑，被拿到的几率都是1/2，所以可能性一样大．”该被试认为“肯定要拿到一个白球”，先入为主地把“第1步”的结果限定为“只能是白球”，这显然忽略了另一种可能性，而导致了错误的判断．

3.2 7~9年级学生概率比较策略的发展

对7~9年级学生各策略的使用频率进行了统计（图2）．由于部分策略的使用频率在各年级中均不高，以下仅对主要的策略发展作讨论．

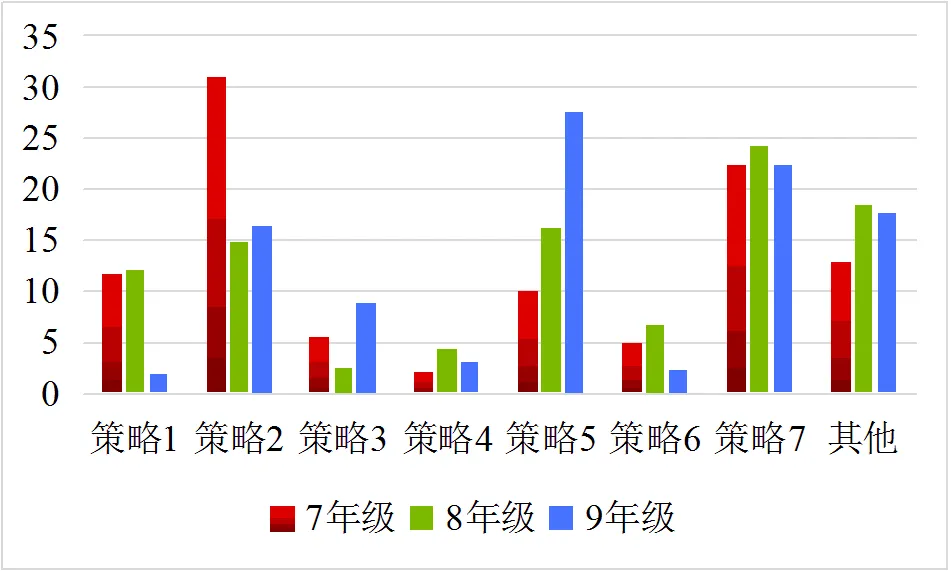
（其中：策略1，认为概率无法预测和量化；策略2，基于数量或比例关系；策略3，基于模糊的样本空间；策略4，分步试验法；策略5，基于精确的样本空间；策略6，局部的分步试验法；策略7，等可能性偏见）

（1）认为概率无法预测和量化．7、8年级学生有近12%的被试认为概率是无法预测和量化的；9年级学生在这一策略上的比例明显减少（不足2%）．

（2）基于数量或比例关系．7年级学生关于这一策略的比例较高（近30%），8、9年级学生在此策略上的比例则显著下降了近一半（15%左右）．

（3）基于模糊的样本空间．7、8及9年级学生此策略的使用频率分别为5.48%、2.46%和8.86%，9年级学生在此策略上的使用频率不降反升．这表明这一朴素策略比较顽固，难以消除．

（4）分步试验法和局部的分步试验法．学生在此策略上的使用频率一直不高，但学生在没有学习“列举法求概率”的情况下能够使用该策略，足以说明了学生的创造力，以及该策略对学生而言是有效的．当然，学生在分步的过程中常常忽略第1步的多种可能性，从侧面反映了其尚缺乏分类讨论的思想，这需要在日常的数学教学中加以渗透．

（5）基于精确的样本空间．该策略的使用频率在7、8及9年级被试中逐级递升（分别为9.82%、16.24%及27.56%），这说明随着对随机性和概率内容认识的加深，学生越来越好地掌握了概率比较策略．

（6）等可能性偏见．总体而言，学生在该策略的使用频率始终处于较高水平（23%左右），且比较顽固，难以消除．这也得到了已有研究[10]的支撑．进一步对两类等可能性偏见的发展进行了深入分析．可以发现，在7、8及9年级被试中，第I类等可能性偏见的使用频率是逐渐减少的（分别为14.76%、14.6%及10.5%），而第II类等可能性偏见的使用频率是逐渐增加的（分别为7.5%、9.76%及11.8%）．

4 讨论与建议

4.1 针对性地消除学生的错误策略

学生在面临概率问题时已然形成和发展了诸多经验或信念[13]，学生在正式学习概率比较相关内容之前所持有的“非正式知识”[14]往往偏离了概率问题的实质，需要在教学中予以纠正．在儿童的认知发展进程中，始终存在一些顽固的、难以消除的错误策略（如，第II类等可能性偏见），而纠正这些策略有一定难度，这需要研究者在教学以及后续研究中持续关注[15~21]．

4.2 帮助学生建立可靠的数学模型

在正式学习概率内容之前，学生的认识不是一块白板，他们已经发展了某种程度的前概念．第一，加强学生对于古典概率“理论先验性”和“可度量性”的理解．研究中，一些被试认为概率不能被预测和量化，坚信它和运气没有差别且无规律可循，想要度量和预测机会是不可能的．教学需要帮助其及时摆脱这种朴素信念，引导其认识到理论概率的先验性和可度量性．第二，通过直观图示发展学生对复杂事件概率的理解．学生在“摸出2个球”问题情境中进行概率比较时遇到了困难，而这些困难一方面源于其无法处理重复样本，一方面源于其难于列举所有的可能结果[9]．也因如此，他们在概率比较时表现出种种错误策略及不良直觉．为此，建议教学尝试设计直观图示帮助学生建立可靠的概率比较模型，充分发挥树状图、二维表及模拟重复试验等直观方法在学生发展概率思维中的作用．

5 不足与展望

研究的被试仅从北京市一所学校选取，研究结果的代表性存在一定局限．后续研究将对学生概率比较的具体策略进行更深入的考察，如等可能性偏见在不同复杂程度问题中的表现及其潜在原因，等等．

致谢：感谢北京市民族学校黄兵彦老师在数据收集及北京师范大学刘梦灵同学在数据录入方面所做的工作．

[1] Nilsson P, Li J. Teaching and Learning of Probability [A]. In: Cho S J.[C]. New York: Springer, 2015.

[2] Australian Education Council.[M]. Carlton, VIC: Curriculum Corporation, 1991.

[3] National Council of Teachers of Mathematics.[M]. Reston, VA: NCTM, 2000.

[4] 中华人民共和国教育部．全日制义务教育数学课程标准（实验稿）[M]．北京：北京师范大学出版社，2001．

[5] 中华人民共和国教育部．全日制义务教育数学课程标准（2011年版）[M]．北京：北京师范大学出版社，2012．

[6] 人民教育出版社课程教材研究所．义务教育教科书（九年级上册）[M]．北京：人民教育出版社，2014．

[7] Conference Board of the Mathematical Sciences (CBMS).[M]. R.I. American Mathematical Society, 2001.

[8] Kvatinsky T, Even R. Framework for Teacher Knowledge and Understanding of Probability [A]. In: Phillips B.[C]. Cape Town, South Africa: International Statistical Institute, 2002.

[9] 何声清，巩子坤．11—14岁学生关于可能性比较的认知发展研究[J]．数学教育学报，2013，22（5）：57-61．

[10] Lecoutre M. Cognitive Models and Problem Spaces in Purely Random Situations [J]., 1992, (23): 557-568.

[11] 李俊．中小学概率的教与学[M]．上海：华东师范大学出版社，2003．

[12] Batanero C, Serrano L. The Meaning of Randomness for Secondary School Students [J]., 1999, 30(5): 558-567.

[13]  Sharma S. Cultural Influences in Probabilistic Thinking [J]., 2012, 4(5): 63-77.

[14]  Amir G S, Williams J S. Cultural influences on Children’s Probabilistic Thinking [J]., 1999, 18(1): 85-107.

[15] 范良火，熊斌，李秋节．现代数学教育中的教材研究：“概念”“问题”和“方法”[J]．数学教育学报，2016，25（5）：1-4．

[16] 方均斌，梁凯，朱玲．数学问题教学的五个探索点[J]．数学教育学报，2016，25（1）：47-50．

[17] 史宁中．试论数学推理过程的逻辑性——兼论什么是有逻辑的推理[J]．数学教育学报，2016，25（4）：1-16．

[18] 朱哲民，贾冰．数学探究教学SIRA评价标准建立的尝试[J]．数学教育学报，2016，25（1）：57-60．

[19] 郑毓信．数学教育视角下的“核心素养”[J]．数学教育学报，2016，25（3）：1-5．

[20] 喻平．数学学科核心素养要素析取的实证研究[J]．数学教育学报，2016，25（6）：1-6．

[21] 陈蓓．课例研究与教师数学学科教学知识（MPCK）的发展[J]．数学教育学报，2016，25（4）：74-78．

[责任编校：周学智]

Probability Comparison Strategy and Its Development for 7-9th Students

HE Sheng-qing1, GONG Zi-kun2

(1. Faculty of Education, Beijing Normal University, Beijing 100875, China;2. Faculty of Science, Hangzhou Normal University, Zhejiang Hangzhou 310036, China)

This study selected 204 7thto 9thgraders as the subjects and focused on strategy and its development on the topic of probability comparison. The study showed that 2 correct and 5 informal strategies were typically used in the probability comparison questions, among which “based on accurate sample space” strategy was developed with grade while some informal strategies (e.g. holding that probability is unpredictable, based on the number relationship, equiprobability bias I) could be eliminated, but still, other informal strategies (e.g. based on partial sample space, equiprobability bias II) were so stubborn that difficult to be eliminated. Suggestions to teaching werere: Eliminating students’ errors gradually and systematically; Strengthening students’ understanding of the “theoretical” and “computability” of probability; Developing students’ understanding of complex probability using visual representations.

7thto 9thgraders; probability comparison; strategy; development

G632

A

1004–9894（2017）02–0041–05

2017–01–09

教育部人文社会科学研究规划基金项目——6—15岁儿童的概率概念认知策略及其发展研究（15YJA880020）；北京师范大学教育学部博士生项目——7~9年级学生的概率素养及其发展研究（15秋-03-13）

何声清（1988—），男，安徽安庆人，博士生，主要从事数学教育研究．