基于HPM教学的学生认知发展个案研究

吴 骏



基于HPM教学的学生认知发展个案研究

吴 骏

（云南师范大学初等教育学院，云南昆明 650092）

数学教学中融入数学史是一个重要的研究课题．在八年级数学教学中，进行数学史融入统计概念教学的实验研究，选取6名学生作为个案研究对象，对其认知发展进行定性分析，结果发现：参与研究的5名学生的认知水平得到明显提高，而有1名学生的认知依旧停留在原有的水平．研究表明，数学史融入统计教学加强了学生对统计概念的理解，促进了学生认知的发展，不过，并非所有学生的认知水平都得到明显提升，可能某些学生收效甚微．

HPM；认知发展；个案研究；SOLO分类法

1 问题提出

数学史融入数学教学的有效性归根到底要经过课堂实践的检验．因此，HPM的一项重要研究工作就是教学实验．其中，关于学生情感变化的研究比较多，所得结论大多是正面的，得到了人们的普遍认可；相对于情感方面，如何检测认知范畴的实验效果是重要的，也是比较困难的．近年，国内外一些学者考察了数学史融入数学教学，对学生数学认知产生的影响[1~4]，但研究涉及的学科领域和研究对象都很有限，还缺乏更多关于学生认知方面的实证研究．Kjeldsen在2012年HPM大会报告中指出，数学史融入数学教学有两个核心问题：如何融入数学史更有利于学生学习；如何使用数学史素材帮助学生学习数学，发展学生的历史意识．可见，寻找数学史融入数学教学的切入点，使之能够提高教学效率正是人们最为关心的问题[5]．

在统计内容的教学中，统计量的计算相对简单，但要真正理解其意义却是困难的[6~9]．已有研究表明，学生对统计概念的理解具有一定的历史相似性[10]，这进一步支持了教师在统计教学中运用数学史的观点．以八年级平均数、中位数和众数等概念为具体教学内容，进行HPM教学实验研究，采用个案研究的方法，考察HPM教学促进学生认知发展的效应．

2 研究方法

2.1 研究对象

Barbin和Groth等人指出，在数学史融入数学教学的过程中，考察学生思维水平的研究应该采用质性的研究方法[11]．为了分析学生认知发展的变化，选取某中等城市的一所初中学校八年级两个班的学生作为研究对象，在教学实验前后对这两个班级的学生进行测试，采用目的性抽样的方法访谈了20名学生，从中选取6名学生作为个案研究对象．在教学实验前对学生进行测试，界定其认知水平，HPM教学实验之后，再次测定其认知水平，并分析认知水平的提升与HPM教学的关系．

2.2 教学案例

采用以下方法设计教学案例：（1）直接采用历史上的数学问题和解法，如古印度人估计大数的故事、《九章算术》中的平分术、估计船员人数问题、货币检查箱的故事、中位数的历史起源、利用指南针确定航海位置、数城墙砖块数目，等等；（2）根据历史材料，编制数学问题，如估计数学测验的总分、寻找质点中位数、鞋子的颜色、员工工资问题、你是“平均学生吗”？身高和体重的问题．（3）在现代情境下，选用体现历史发生思想的数学问题，如帽子平均数问题、公共汽车载客量问题、献爱心捐款活动[12]．

对于数学史的运用，数学教学中所追求的不应是真实历史的简单重现，而应是历史的适当重建，这就是指，数学史的适当“改造”应看成是数学史融入数学教学的一个基本途径[13]．由于学生缺乏统计概念的历史背景知识，他们也拥有前人未知的一些知识，因此，研究中更多地采用后两种方法设计教学案例，注重把历史现象转化为有意义的教学现象．

2.3 测试工具

在Watson、Zawojewski、Marnich、曲元海等人研究的基础之上[8，14~16]，把学生对平均数、中位数和众数的理解划分成本意理解、选择使用和问题解决3种水平，并编制了两套平行试卷，分为前测和后测，在教学实验前后进行测试，测试题的归类和数量如表1所示．两份问卷设计完毕之后，分别寄给不同的专家征求意见．试测之后，对题目又作了一些修改才正式施测．

表1 前后测试题的水平及其数量

2.4 数据处理

Groth和Bergner在考察小学职前教师对统计概念的理解时，采用SOLO水平的分析框架：单一结构水平（U）、多元结构水平（M）、关联水平（R）、拓展抽象水平（E）[11]．Watson和Moritz研究学生对平均数理解的纵向发展时，把SOLO分类法划分为6个水平：（1）前结构水平；（2）单一结构水平；（3）多元结构水平；（4）表征水平；（5）应用水平1；（6）应用水平2[17]．

在测试和访谈中发现，有相当一部分学生的认知水平介于多元结构水平和关联结构水平之间，为了更好地区分这些学生的认知水平，有必要在其间设立过渡水平，也可称为前关联水平，用T表示．另外，为了更好地考察学生对统计量的运用，把该阶段分为两个应用水平A1和A2，具体描述见表2．测试题也划定了最高限度水平，见表3．学生对统计概念的理解，单从测试卷的回答中很难准确判断学生达到的认知水平，因此，结合测试之后的访谈，从总体上界定学生达到的认知水平．

表2 学生对集中量数认知水平的描述

表3 每道题目的最高限度水平

3 结果与分析

3.1 教学实验前学生的认知水平

教学实验前对两个班学生进行测试和访谈，按照学生认知水平的人数比例来划分个案研究人数，即U水平的1人，M、T水平各2人，R水平1人，如表4所示．以下以江同学、尹同学、陈同学和柳同学为例，逐一分析他们教学实验前后达到的认知水平．

表4 前测中学生的认知水平

前测及访谈结果表明：江同学能够从总体上理解平均数、中位数和众数是表示集中趋势的统计量，认识到平均数比中位数更易受极端值的影响，能够正确选择使用平均数、中位数和众数，其认知水平达到R水平．以下是其中的一段访谈：

研究者：平均数、中位数和众数这3个概念有什么共同的特征吗？

江同学：代表平均水平．

尹同学了解平均数、中位数和众数的概念，但不清楚它们的用途，还存在一些错误认识，如高于平均数就表示超过了一半的人数（如下述第1题），平均数应该具有实际意义等，她仅达到U结构水平．

第1题．有19位同学参加歌咏比赛，所得的分数互不相同，取得分数排在前10名的同学进入决赛，某同学知道自己的分数后，要判断自己能否进入决赛，他需要知道这19名同学比赛成绩的平均数、中位数还是众数？说明理由．

研究者：你为什么选择平均数？

尹同学：要把所有的成绩用上，就要计算平均数．

研究者：知道了平均数又如何呢？

尹同学：高于平均分就进入决赛．

陈同学基本能理解平均数、中位数和众数的概念，能够运用这3个概念去解决相关问题（如下述第2题），但还存在一些模糊认识，如平均数就是大多数等，还不能从总体上把握它们的特征，他的认知水平为M水平．

第2题．某班学生去登山，他们顺着台阶拾级而上，每个同学边爬边数台阶，最后每个同学都得到一个数字，则台阶级数可以由这组数据的平均数、中位数和众数中的哪一个表示出来？说明理由．

陈同学认为，数台阶一个比较简单的问题，每个人数的台阶数不会差异太大，出现次数最多的就是正确的，也就是由众数来确定台阶级数是合理的．中位数是一组数据中间的数，不一定是正确的．如果使用平均数，那么有些人数的多了，有些人数的少了，会对平均数的计算产生影响，而且平均数还可能是一个小数，就更无法表示台阶数了．

柳同学能用平均数、中位数和众数去解决简单问题，对概念的本意理解有了一些正确的认识（如下述第3题），但她还没有认识到这3个概念的代表性特征，她的认知水平达到T水平．

第3题．一个教师为了调查某镇每个家庭的平均孩子数，他数出这个镇上所有的孩子个数，然后再除以家庭总数50，得到每个家庭的平均孩子数为2.2．

柳同学对这个问题的一些认识：平均数为2.2并不一定代表有一半家庭孩子个数超过2个；有3个孩子的家庭不一定比有2个孩子的家庭多；平均数并不代表精确值，即2.2为平均值，不具有实际意义；孩子总数除以50等于2.2，则孩子总数为2.2×50=110．

3.2 教学实验后学生的认知水平

在第二次访谈中，关注数学史融入数学教学实验之后，学生在哪些方面取得了进步，以及产生进步的原因．后测及访谈结果表明：

江同学进一步巩固了对这3个概念的理解，对概念的选择使用有了较大的进步，她成功地解决了后测中的两个复杂问题，认知水平达到了A2水平．以下是江同学对第5题回答的访谈：

第5题．某电影院5天的观众分别为：72人、97人、70人、71人、100人，求出平均数、中位数和众数，你认为用哪一个数能更好地反映这5天每天看电影的观众人数？说明理由．

研究者：你答题时说取平均数误差小，为什么？

江同学：因为算出来的平均数为82，在这组数据中处于中间位置，它与97和100的差距较小，因此选择平均数．

研究者：为什么不选择中位数？

江同学：中位数72与97和100的差距较大，故不用．

江同学的认知发展概述如表5所示．

尹同学能利用这3个概念去解决简单问题，但还存在一些模糊认识，不了解这3个概念能够表示数据的集中情况，不能区分平均数和中位数的选择使用，她的认知水平仅达到M水平．

研究者：平均数和中位数有什么区别？

尹同学：平均数表示平均情况，中位数表示中间位置的数．

研究者：平均数、中位数和众数这3个概念反映了一组数据的什么特征？

尹同学：总体情况．

尹同学的认知发展概述如表6所示．

陈同学不能区分平均数和中位数的使用，仅知道平均数易受极端值的影响，而不清楚中位数不易受极端值的影响，对中位数的运用仅限于寻找中间位置．他并未理解这3个数都是表示集中趋势的量，也不能区分它们之间的选择使用，他的认知水平仍然停留在原来的M水平．以下是陈同学对第4题回答的访谈：

第4题．某人11天看电视的时间分别为：45，256，52，45，57，48，67，66，58，55，17（单位：分钟），用平均数、中位数和众数中的哪一个数最能描述他看电视的时间？说明理由．

研究者：这组数据有什么特点？

陈同学：没有看出来．

研究者：什么情况下选用中位数？

陈同学：寻找中间位置的时候．

陈同学的认知发展概述如表7．

表5 江同学的认知发展概述

表6 尹同学的认知发展概述

表7 陈同学的认知发展概述

柳同学已经认识到这3个概念表示数据的平均水平，认识到一组数据中存在极端值的情况下要用中位数，而且在下述第7题中能利用“减多益少”的方法解决单个复杂问题，她的认知水平达到A1水平．

第7题．有7幢建筑物的高度如图1所示（单位：米）．问：请你估计它们的平均高度是多少？说明你是如何估计这个高度的．

研究者：如何估计建筑物的高度？

柳同学：把第2幢建筑多的部分补到第1幢上，再把第5幢多余的部分补到第3、6和7幢上．我估计建筑物的高度为26米．

柳同学的认知发展概述如表8所示．

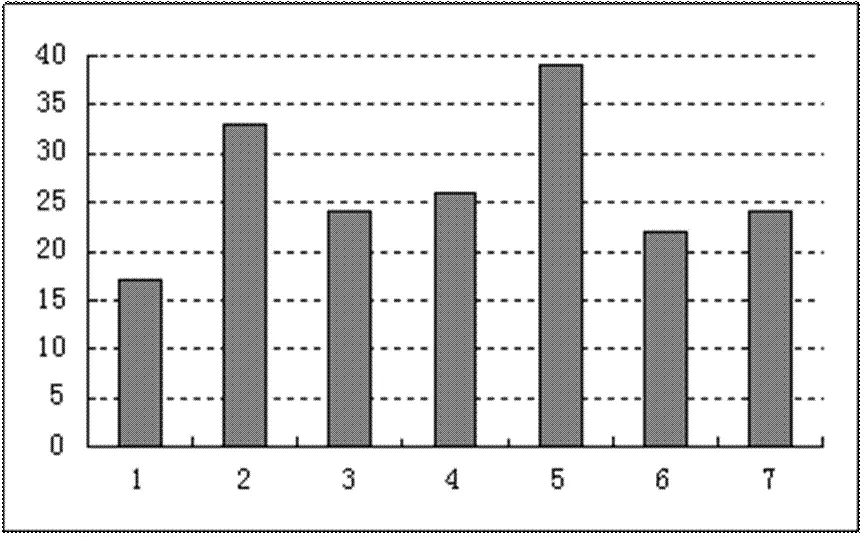
图1 建筑物的高度

3.3 教学实验前后学生认知发展水平的比较

教学实验前后学生的认知发展水平见表9所示．研究表明，参与数学史融入数学教学实验的5名学生明显加强了对平均数、中位数和众数的理解，其中1名学生发展到研究划分的最高认知水平，另外4名学生的认知水平也分别提高1~3个层次不等．然而，数学史融入统计教学的效果也并非都是明显的，有1名学生的认知水平依旧停留在原有的水平．通过对学生认知发展原因的探究，发现每个学生的进步记录都与研究设计的教学案例有关．尽管有一名同学的认知发展并不显著，但从他的认知发展概述中可以看出，他已经认识到众数可以表示非数字类型，中位数把数据分成个数相等的两半，其驱动力正是研究设计的教学案例．

4 结 论

研究结果表明，数学史融入统计教学加强了学生对统计概念的理解，促进了学生认知的发展．不过，当把融入数学史作为一种教学手段时，并非所有学生的认知水平都得到明显提升，可能某些学生收效甚微，但利用数学史素材设计的教学案例，可能也为学生创造了一种积极和有效的学习环境．需要注意的是，数学史融入数学教学是一个长期回应的过程，很难在短期产生明显的效果，不能奢望学生在一夜之间获得较高的考试分数，但它确实可以让学生体验到学习数学是一个有意义的、充满活力的过程，从而使学习变得更容易和更深入．

表8 柳同学的认知发展概述

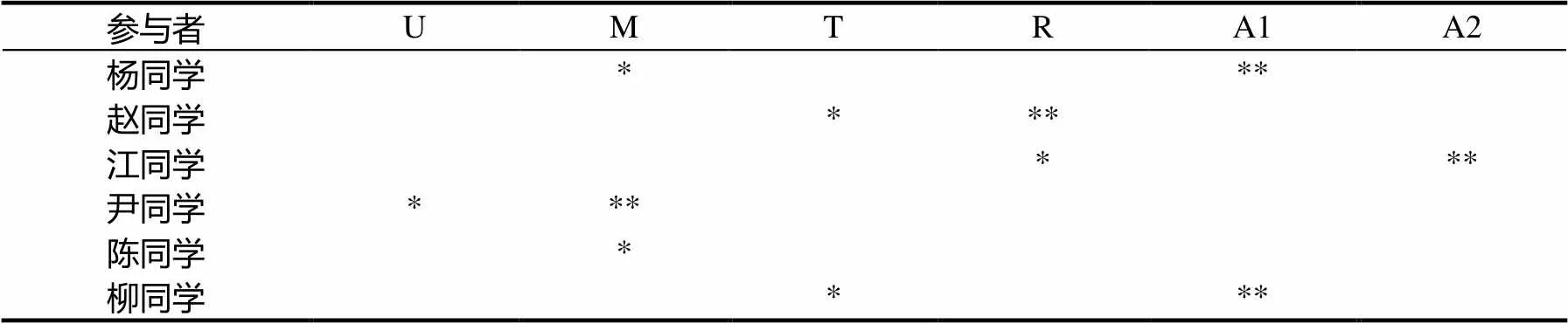
表9 教学实验前后学生认知发展水平的比较

注：*表示前测认知水平，**表示后测认知水平

[1] Furinghetti F. History of Mathematics, Mathematics Education, School Practice: Case Studies Linking Different Domains [J]., 1997, 17(1): 55-61.

[2] Kidron I. Polynomial Approximation of Functions: Historical Perspective and New Tools [J]., 2003, (8): 299-331.

[3] Reed B M. The Effects of Studying the History of the Conception of Function on Student Understand the Concept [D]. Ph.D. Thesis, Kent State University, 2007.

[4] 龚运勤，唐振球．架起数学史成为提高中学生数学学业成绩的桥梁[J]．数学教育学报，2011，20（6）：32-35．

[5] 吴骏，汪晓勤．国外数学史融入数学教学研究述评[J]．比较教育研究，2013，（8）：78-82．

[6] 梁绍君．“算术平均数”概念的四个理解水平及测试结果[J]．数学教育学报，2006，15（3）：35-37．

[7] 吴骏．小学四年级学生对平均数概念理解的发展过程[J]．数学教育学报，2011，20（3）：39-42．

[8] 曲元海，项昭，李俊扬，等．初中生学习统计量理解水平的调查分析[J]．数学教育学报，2006，15（1）：35–37．

[9] 吴颖康，李凌．上海高中生对集中量数的理解[J]．数学教育学报，2011，20（6）：25-28．

[10]  Bakker A. Design Research in Statistics Education—On Symbolizing and Computer Tools [D]. Ph.D. Thesis, The Freudenthal Inistitute, Utrecht, 2004.

[11]  Groth R E, Bergner J A. Preservice Elementary Teachers’ Conceptual and Procedural Knowledge of Mean, Median, and Mode [J]., 2006, (8): 37-63.

[12] 吴骏．基于数学史的统计概念教学研究——以平均数、中位数和众数为例[D]．华东师范大学，2013．

[13] 郑玮，郑毓信．HPM与数学教学中的“再创造”[J]．数学教育学报，2013，22（3）：5-7．

[14]  Watson J M, Moritz J B. The Developments of Concepts of Average [J]., 1999, 21(4): 15–39.

[15]  Zawojewski J S, Shaughnessy J M. Mean and Median: Are They Really so Easy [J]., 2000, 5(7): 436–440.

[16]  Marnich M A. A Knowledge Structure for the Arithmetic Mean: Relationships between Statistical Conceptualizations and Mathematical Concepts [D]. Doctoral dissertation, University of Pittsburgh, 2008.

[17]  Watson J M, Moritz J B. The Longitudinal Development of Understanding of Average [J]., 2000, 2(1&2): 11-50.

[责任编校：周学智]

Case Study on Students’ Cognitive Development Based on HPM Instruction

WU Jun

(College of Primary Education, Yunnan Normal University, Yunnan Kunming 650092, China)

Integrating the history of mathematics in teaching and learning of mathematics was always a central topic of HPM. The research explored case of six students in eighth grade of junior high school based on HPM instruction. The case of six students showed that five students’ understanding of mean, median and mode were notably strengthened, one of them moved an entire cognitive level, four students’ cognitive levels were increased respectively by 1 and 3 levels, and another one did little growth. The research showed that it was an important cause to promote the students’ cognitive ability which mathematics history integrated into teaching of statistics concepts.

HPM; cognitive development; case research; SOLO taxonomy

G420

A

1004–9894（2017）02–0046–04

2017–01–12

全国教育科学规划教育部重点课题——边疆少数民族地区小学数学教学中融入数学文化的调查研究（DMA150217）

吴骏（1968—），男，云南宣威人，教授，博士，硕士生导师，主要从事概率统计教学、数学史与数学教育研究．