数学“四基”的研究现状及展望

曾 峥，杨豫晖，武金艳



数学“四基”的研究现状及展望

曾 峥1，杨豫晖2，武金艳3

（1．佛山科学技术学院，广东佛山 528000；2．海南师范大学，海南海口 571158；3．海口市琼山三小，海南海口 571100）

数学“四基”是近年来中国数学教育研究的重点与热点问题之一，特别是《义务教育数学课程标准（2011年版）》正式发行后，对数学“四基”的研究更为丰富．以数学“四基”为关键词在中国知网上筛选出相关文献194篇，这些成果对数学“四基”的研究大致分为：数学“四基”的形成发展研究，数学“四基”内涵研究，数学“四基”关系研究和数学“四基”教学研究等4个方面，对这些研究成果进行结构化梳理和分析，为进一步的研究提供借鉴．

数学“四基”；内涵；关系；教学实践

《义务教育数学课程标准（2011年版）》（以下简称“2011版课标”）指出：通过义务教育阶段的数学学习，学生能：获得适应社会生活和进一步发展所必需的数学的基础知识、基本技能、基本思想、基本活动经验[1]，即在“双基”的基础上，明确提出“四基”课程目标．2013年6月召开的“未来十年中国数学教育展望”和2014年5月召开的“首届华人数学教育会议”也安排了数学“四基”的讨论专题．由此可见，数学“四基”已成为中国数学教育研究的重点和热点．相关文献的研究方向和内容主要涵盖了数学“四基”的形成发展研究，数学“四基”内涵研究，数学“四基”关系研究和数学“四基”教学研究等4个方面．

1 数学“四基”的形成与发展

数学“四基”是对数学双基的继承和发展，与此相关的文献主要采用历史法和文献法进行分析．梳理如下：

1.1 数学双基的形成与发展概述（1952—2000年）

数学双基的形成与发展大致经历了4个阶段：

1952年颁布的《中学数学教学大纲（草案）》中首次明确提出“基础知识”和“技能”要求，“双基”一词并未提出[2]．同年颁布的《小学算数教学大纲（草案）》中提出：保证儿童自觉地和巩固地掌握算术知识和直观几何知识，并使他们获得实际运用这些知识的技能[3]．这是（小学）数学“双基”的最初形式．

1963—1982年，“双基”逐步形成，教材和教学体现“双基”．1978年《全日制十年制学校小学数学教学大纲（试行草案）》，1980年《全日制十年制学校中学数学教学大纲（试行草案）》和1982年《全日制六年制重点中学数学教学大纲（征求意见稿）》都对“双基”教学的要求逐步细化．该阶段的教材扎扎实实地加强了基础知识和基本训练，内容比较充实，阐述比较严谨、细致，突出了“双基”[4]．

1986—1988年：明确界定“双基”，教材和教学强化双基．1986年，《全日制中小学数学教学大纲》把教学目的界定为“双基+三大能力+其他”的结构，此后的大纲都沿用了“数学的基础知识和基本技能”这一表述．1988年《九年制义务教育全日制初级中学数学教学大纲（初审稿）》第一次明确界定了数学双基教学的含义．

1992—2000年：“双基”细化，双基教学异化．该阶段的教学大纲主张降低“双基”的难度，删除繁、难、偏、旧内容．但是在实际教学中，由于高考竞争加剧和唯分数论思想的泛滥，双基教学实践开始过度强调记忆、过度强化训练，出现“题海战术”、“应试双基”等异化现象[2]．

1.2 数学双基向数学“四基”逐步转化（2001—2011年）

2001年《全日制义务教育数学课程标准（实验稿）》（以下简称“实验稿”）把“双基”的含义明确为：经历将一些实际问题抽象为数与代数问题的过程，掌握数与代数的基础知识和基本技能，并能解决简单的问题……[5]对数学双基的表述更加细致．

同时，实验稿在课程总体目标的第一条表述到：通过义务教育阶段的数学学习，学生能够获得适应未来社会生活和进一步发展所必需的重要数学知识（包括数学事实、数学活动经验）以及基本的数学思想方法和必要的应用技能．这条目标包含了两个信息：一是在总体目标的表述中已经包含了重要的数学知识、数学事实、数学活动经验、基本的数学思想方法和必要的应用技能等提法，虽排列尚不够清晰，但明确地体现出自20世纪90年代中期以来，以《21世纪中国数学教育展望》为代表的中国数学课程改革的阶段性研究成果，以及专为实验稿研制开展的若干项重大基础性研究的成果[6]．二是“数学活动经验”没有单列，而是作为数学知识的重要组成部分在括号里出现，反映了当时实验稿研制者们更为关注知识观的变革，另一方面当时围绕“活动”积累的“经验”还不多．由此可见，实验稿的颁布标志着数学“四基”进入萌芽期．

2004年教育部根据《中共中央国务院关于进一步加强和改进未成年人思想道德建设的若干意见》和教育部关于贯彻这一文件的《实施意见》，开始对实验稿进行第一次修订，把总体目标的第一条修改为：通过义务教育阶段的数学学习，学生能够获得适应未来社会生活和进一步发展所必需的数学知识、数学活动经验、基本的数学思想方法和必要的应用技能．此次修改把“数学活动经验”与知识、思想、技能并列，已经形成了“四基”的基本轮廓[6]．但是此次修订因为种种原因并没有成功．

2007年4月，在宁波数学教育高级研讨班上史宁中教授在题为“《数学课程标准》的若干思考”报告中指出：如果在中国中小学数学教育中，一方面保持“数学‘双基’教学”这个合理内核，另一方面添加“基本思想”和“基本活动经验”，出现既有“演绎能力”又有“归纳能力”的培养模式，就必将出现“外国没有的我们有、外国有的我们也有”的局面，到了那一天，我们就能自豪地说，中国的基础教育领先于世界[7]．数学“基本思想方法”和“基本活动经验”再一次被强调．其中，2005年4月20日，教育部就成立了以史宁中教授为组长的《数学课程标准》修订组．

2011年12月，教育部正式颁布2011版课标，标志着中国数学基础教育课程目标从重视“双基”发展为重视“四基”．2011版课标对“四基”进行了完整、清晰、准确的描述：通过义务教育阶段的数学学习，学生能获得适应社会生活和进一步发展所必需的数学的基础知识、基本技能、基本思想、基本活动经验[1]．

2 数学“四基”的内涵

基础知识和基本技能是从数学双基中继承下来的，在数学“四基”的背景下基础知识的内涵虽然发生了一些细微变化，但对其内涵界定学术界持统一观点，把基础知识界定为：数学中的基本概念、基本性质、基本法则、基本公式、基本定律和基本定理等．把基本技能界定为：按照一定的程序与步骤进行运算、推理、作图、处理数据等心智活动方式[8]．

基本思想和基本活动经验是对数学双基的发展，在课标修订版中并没有明确说明什么是数学基本思想、数学思想有哪些，什么是数学基本活动经验．表1列举了几种目前国内对基本思想和基本活动经验的认识和看法．

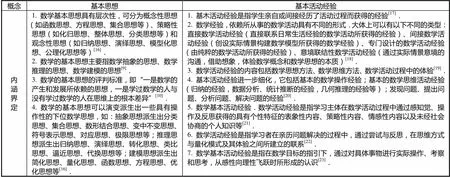
表1 基本数学思想和基本数学活动经验的内涵

目前国内公认的数学基本思想主要有3大类：数学抽象的思想、数学推理的思想和数学建模的思想．对数学基本活动经验虽然还没有形成共识，但有几点是共同的：

第一，基本活动经验是在特定的数学活动中积累的．这些活动必须有明确的数学内涵和数学目的，体现数学的本质；第二，基本活动经验是一种组合体，包括了数学活动中的主观体验以及获得的客观认识；包括数学活动的结果，更包括活动的过程；第三，数学活动经验的类型目前还没有统一，但其核心应该是如何思考的经验，促进学生学会运用数学的思维方式进行思考；第四，数学活动经验最终可以帮助学生建立自己的数学现实和数学学习的直觉，这种直觉一旦生成，那么在后续的学习和问题解决中将起到重要作用；第五，基本活动经验的积累，大致需要经过“经历、内化、概括、迁移”的过程[24]．

3 数学“四基”的相关关系探讨

数学“四基”的关系可分为数学“四基”的内部关系和数学“四基”的外部关系．

3.1 数学“四基”的内部关系

对于数学“四基”的内部关系主要有以下几种认识：

（1）“基础知识、基本技能”是显性目标，而“基本思想、基本活动经验”是隐性目标[25]．

“四基”的基本形式是一个三维模块，学生头脑里的数学大厦，是在一个个的基础模块之上建立起来的．数学基本知识的积累过程、基本技能的演练过程和基本数学思想方法的形成过程形成了3个维度，基本数学活动经验本身并不构成一个单独的维度，而是填充在三维模块中间的粘合剂．学生通过无处不在的基本数学活动获得的经验，与数学基本知识、基本技能、基本思想方法交织在一起，渗透在整体数学学习过程中，如图1所示[26]．

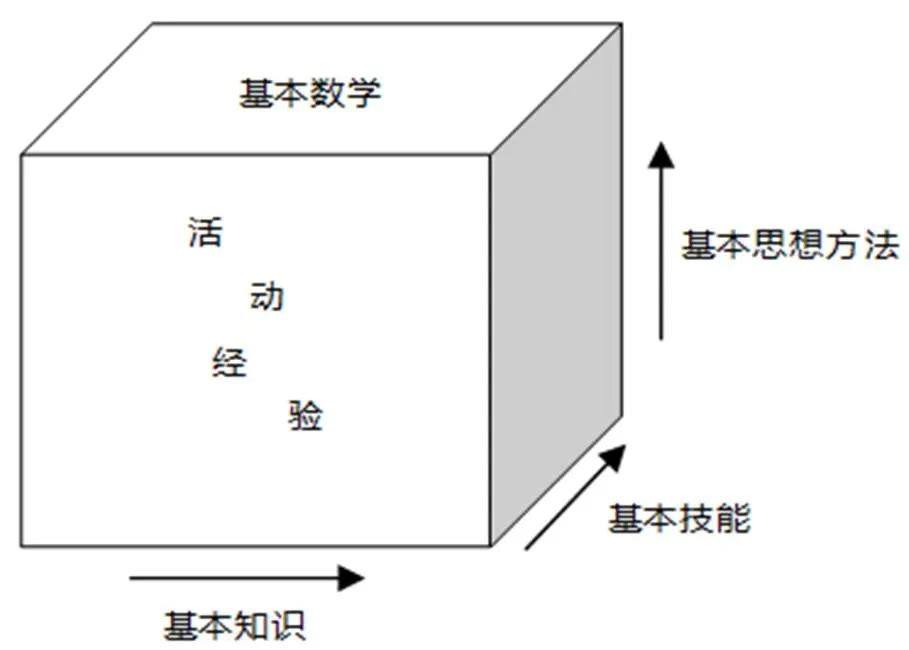
图1 四基模块示意图

（2）数学“四基”是相辅相成、和谐统一、螺旋递进的关系．

由于数学知识的抽象性，在数学学习过程中，学生需要通过动手操作学具或画图等直观手段，引发相应的数学思考，从而帮助理解所学的数学知识，并在数学知识的实践与运用过程中获得基本技能[11~15]．在基本技能获得的过程中，学生不仅积累了操作活动经验，而且积累了重要的思维活动经验，尤其是积累了抽象的经验、归纳的经验和演绎的经验等基本活动经验，这些活动经验都是后续数学学习的重要基础．当数学活动经验积累到一定程度，将在学生脑海里促进形成某种较为稳固的思维模式，这就形成了数学思想，当数学思想形成后，将进一步改良学生己有的认知结构，进一步完善己经形成的知识体系，同时，将从策略和方法上更好地促进新的数学知识的学习和新的技能的获得，具体如图2所示[16]．

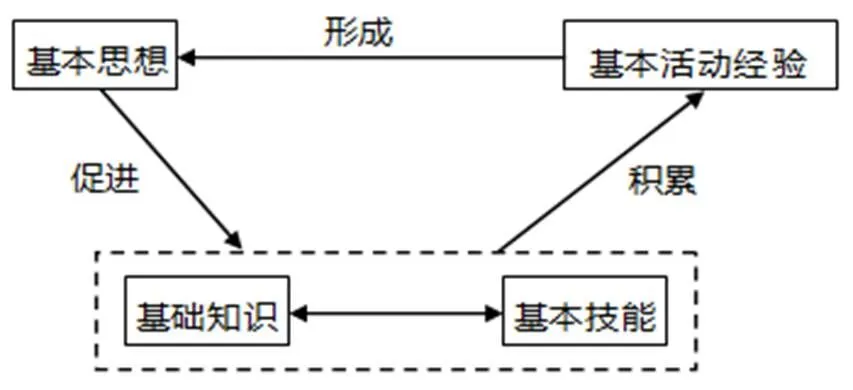
图2 “四基”内部关系

（3）数学“四基”是知识系统和经验系统的有机体．

基础知识和基本技能形成了学生的知识系统，而基本活动经验形成的是经验系统，两个系统有机结合、相互促进才构成完整的数学知识结构．这个结构形成的纽带，就是数学活动．所以，数学活动的过程就是“经验化”的过程．“双基”只有通过经验化，才能够真正成为学生的数学素养．但是由于学生的原始经验是模糊的、片面的、不严谨的，所以要使“基本活动经验”更加确切、有效并且合理，就需要经历一个形式化与概念化的过程．由于数学知识本来具有确定性和严谨性，所以经历了形式化和概念化的“基本活动经验”才能够很好地融入“双基”之中．两个系统相互促进、相互结合才能让学生获得完整的数学知识．如图3所示[27]．

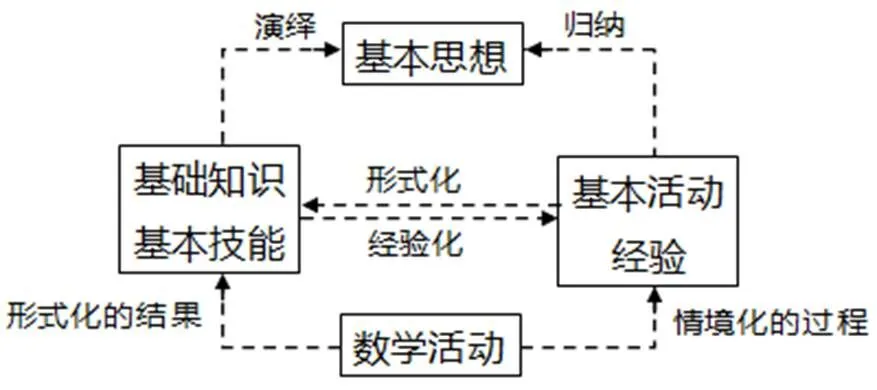
图3 数学“四基”的关系结构

3.2 数学“四基”的外部关系

数学“四基”的外部关系主要指“四基”与数学课程“三维”目标之间的关系．

数学“四基”与数学课程“三维”目标联系密切，数学“四基”内部的相辅相成、和谐统一和螺旋递进的关系，促进了数学课程“三维”目标的整体实现．“四基”中的“基础知识”和“基本技能”对应着“三维”目标中的“知识与技能”维度，“基本思想”和“基本活动经验”对应着“三维”目标中的“过程与方法”维度．教师在“双基”教学基础上，通过融入“基本思想”、“基本活动经验”的教学，将更好地促进学生对“基础知识”、“基本技能”的理解、掌握和运用，更好感悟数学的基本思想，积累数学的基本活动经验，体会数学的神奇与魅力，体会数学的价值，获得成功的体验，提高学习的兴趣，增强学习的信心，从而促进“三维”目标中的“情感与态度”目标的达成．

因此，数学“四基”内部的和谐统一将更好促进外部“三维目标”的整体达成，它们之间的关系如图4所示[16]．

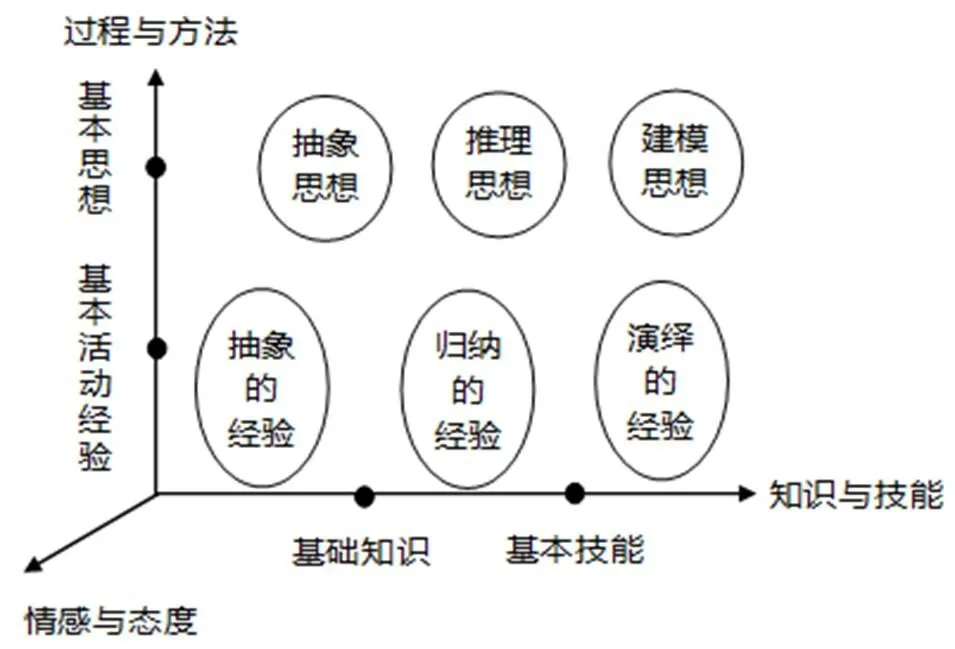
图4 数学“四基”与“三维”目标关系

4 数学“四基”的教学实践

数学“四基”要从理论走向实践，才能更好体现其价值，查阅与数学“四基”相关并发表于核心期刊的22篇文献，其中与数学“四基”教学相关的文献有12篇，关注最多的主题是教学中怎样有效渗透数学思想和数学活动经验，并且多以课为例．

在教学中如何积累学生的数学活动经验的观点主要有以下几种：

（1）参与建构，积累感性经验——经历扩展，积累估测经验——自主探索，积累迁移经验——解决问题，积累思辨经验[28]；

（2）经历探究，积累直接经验——巧设情景，丰富间接经验——内培外引，提升思维经验——尊重起点，避免经验越位[29]；

（3）顺应多数学生的观点，激活数学活动经验——放大少数学生的思路，提升数学活动经验[30]；

（4）巩固旧知，激活“经验”——操作实践，拓展“经验”——顺应新知，建构“经验”——返璞生活，提升“经验”[31]；

对教学中如何渗透数学思想有以下几点建议：

（1）教师要适时寻求数学思想渗透的可行性，重视数学思想的渗透与学生感悟的过程性，引导学生在反思中提炼数学思想[32]；

（2）在背景展示中揭示数学思想，在知识探索中渗透数学思想，在实践操作中形成数学思想[33]；

（3）课堂教学中渗透数学思想的语言，不同于讲解数学思想的语言．数学思想不是在讲授知识时生拉硬扯、牵强附会地阐述的，而是融入其中，因势利导、水到渠成地渗透的，也不是摆开架势、长篇大论地传授的，而是潜移默化、画龙点睛地渗透的[34]；

（4）教学中应该从整体着眼，把数学基木思想真正看成教学的有机组成，有目的、有计划地、连续地进行数学思想渗透活动[35]．

5 研究展望

综上可知，目前对数学“四基”产生背景的研究较为全面，对基础知识和基本技能的内涵界定也非常明确，对数学基本思想和基本活动经验内涵的探讨以及对数学“四基”内外部关系的探讨虽然还没有完全达成共识，但形成了一些共同观点．另外，对数学“四基”教学的案例讨论也较为丰富，突出了数学“四基”教学的理论与实践的融合性[36~46]．

当然，也应该清醒认识到目前研究尚存在如下问题．

首先，缺乏数学“四基”教学系统全面的研究．现有文献基本都是以某一课为例进行剖析并提出教学建议，缺少对数学“四基”教学的共性研究、顶层设计以及操作策略研究．

其次，缺失数学“四基”教学的评价研究．数学教学是否真正落实了四基，学生在教学中是否真正达成了数学“四基”目标，目前文献尚少提及．

因此，有关数学“四基”的研究还需要进一步深化和拓展．

（1）“基本思想”和“基本活动经验”的内涵研究仍然需要持续和深入，应该进一步明确数学“四基”，特别是基本思想和基本活动经验的内涵与外延，对2011版课标有关“基本思想”和“基本活动经验”的案例进行补充，帮助教师更好地理解和落实“四基”．

（2）深度挖掘“四基”的内部关系．“基本思想”和“基本活动经验”是在“双基”的基础上新增的两个“基本”，在教学中重点关注这两个“基本”的思路是正确的，但是在关注“基本思想”和“基本活动经验”的同时，不能忽视“基础知识”和“基本技能”的发展与落实．需要进一步厘清“四基”的内部逻辑关系，把“四基”作为一个有机整体进行研究和落实．

（3）拓展“四基”的外部关系研究．比如，“四基”与核心素养的关系、“四基”与数学文化的关系，“四基”与数学素养的关系，“四基”与创新意识和能力的关系等，这些研究都将为良好的数学教育提供有力支撑．

（4）提升数学“四基”的教学实践研究．围绕体现数学“四基”的教学设计、教学实施和教学评价进行相关研究，突出数学“四基”教学的共性研究、顶层设计以及操作策略研究，在提升理性认识的基础上更方便一线教师操作迁移；由于数学“四基”在教学实践中的落实是其提出的根本诉求，因此要关注数学“四基”教学的评价研究，特别是“基本思想”和“基本活动经验”属于隐性目标，其在教学中的显性评价的诉求更为迫切．

[1] 中华人民共和国教育部．全日制义务教育数学课程标准（2011年版）[M]．北京：北京师范大学出版，2011．

[2] 杨豫晖．数学双基教学的发展、争鸣与反思[J]．中国教育学刊，2010，（5）：34-37．

[3] 课程教材研究所．20世纪中国中小学课程标准·教学大纲汇编·数学卷[M]．北京：人民教育出版社，2001．

[4] 李润泉，陈宏伯，蔡上鹤，等．中小学数学教材五十年：1950—2000[M]．北京：人民教育出版社，2008．

[5] 中华人民共和国教育部．全日制义务教育数学课程标准：实验稿[M]．北京：北京师范大学出版，2001．

[6] 孙晓天．“四基”：十年数学课程改革最重要的收获[J]．基础教育课程，2011，（Z2）：34-37．

[7] 张奠宙，何文忠．交流与合作——数学教育高级研讨班15年[M]．南宁：广西教育出版社，2009．

[8] 宋乃庆，张奠宙．小学数学教育概论[M]．北京：高等教育出版社，2008．

[9] 中华人民共和国教育部．义务教育数学课程标准（2011年版）解读[M]．北京：北京师范大学出版社，2012．

[10] 史宁中．数学思想概论（第一辑）：数量与数量关系的抽象[M]．长春：东北师范大学出版社，2008．

[11] 王光明，张楠，周九诗．高中生数学素养的操作定义[J]．课程·教材·教法，2016，（7）：50-55．

[12] 王光明，廖晶．“探索世界”范式及其对数学教育的启示——ICME12获奖报告述评[J]．课程·教材·教法，2013，（12）：116-119．

[13] 王光明，宋金锦，佘文娟，等．建立中学数学英才教育的数学课程系统——2014年中学英才教育数学课程研讨会议综述[J]．课程·教材·教法，2014，（5）：122-125．

[14] 王光明，佘文娟，宋金锦．基于NVivo10质性分析的高效数学学习心理结构模型[J]．心理与行为研究，2014，（1）：74-79．

[15] 王光明，张晓敏，王兆云．高中生高效率数学学习的智力特征研究[J]．教育科学研究，2016，（3）：48-55．

[16] 苏明强．数学“四基”的内涵、关系与应用[A]．北京师范大学．首届华人数学教育会议论文集[C]．北京师范大学，2014．

[17] 史宁中，柳海民．素质教育的根本目的与实施路径[J]．教育研究，2007，（8）：10-14，57．

[18] 张奠宙，竺仕芬，林永伟．“基本数学经验”的界定与分类[J]．数学通报，2008，（5）：4-7

[19] 单肖天，景敏．数学活动经验及其对教学的影响[J]．课程·教材·教法，2008，（5）：41-44．

[20] 徐斌艳．面向基本数学活动经验的教学设计[J]．中学数学月刊，2011，（2）：1-4．

[21] 朱黎生，沈南山，宋乃庆．数学课程标准“双基”内涵延拓的教育思考[J]．课程·教材·教法，2012，（5）：41-45．

[22] 王新民．论数学活动经验的基本内涵及其形成条件[J]．课程·教材·教法，2013，（11）：55-60．

[23] 张奠宙．数学“双基”教学的理论与实践[M]．南宁：广西教育出版社，2008．

[24] 张丹．数学课程目标：从“双基”到“四基”从“两能”到“四能”[J]．中小学管理，2012，（4）：10-12．

[25] 崔英梅，孔凡哲．“四基”理论实践探索中问题分析与改进对策[J]．中国教育学刊，2014，（3）：53-57．

[26] 张奠宙，郑振初．“四基”数学模块教学的构建——兼谈数学思想方法的教学[J]．数学教育学报，2011，20（5）：16-19．

[27] 于佳．面向基本数学活动经验的教学设计的若干问题研究[D]．陕西师范大学，2013．

[28] 蔡文美．经历认知过程积累数学经验——“面积单位”的教学探索[J]．教学与管理，2012，（29）：51-53．

[29] 孙春恋．例谈学生基本数学经验积累的课堂指导[J]．教学与管理，2012，（26）：41-43．

[30] 陈赛．让学生的“数学活动经验”生根发芽[J]．教学与管理，2012，（29）：45-46．

[31] 吕程，蔡庆有．思维经验：数学活动经验的内在精髓[J]．教学与管理，2013，（29）：37-39．

[32] 卢杰夫．教学有形思想无形——例谈小学数学教学中数学思想的渗透[J]．山西教育（教学），2014，（12）：51-52．

[33] 康克．思想就在身边——例谈数学思想的教学演绎[J]．广西教育，2015，（1）：61．

[34] 顾沛．小学数学教学也要注重渗透数学思想[J]．小学教学（数学版），2012，（Z1）：14-18．

[35] 胡晓敏．谈小学计算教学中数学基本思想的理解与落实[J]．数学学习与研究，2014，（6）：60-61．

[36] 章勤琼，徐文彬．试论义务教育数学教师专业素养及其结构——基于教师专业标准与数学课程标准的思考[J]．数学教育学报，2016，25（4）：69-73．

[37] 黄友初．教师课堂教学行为的四个要素[J]．数学教育学报，2016，25（1）：72-74．

[38] 吴立宝．初中数学教材代数内容的国际比较研究[J]．数学教育学报，2016，25（4）：33-36．

[39] 顾继玲．聚焦“基本数学活动经验”[J]．数学教育学报，2016，25（1）：34-37．

[40] 吕宝珠．中学数学教师对数学和科学课程整合态度的调查——以优质中学为例[J]．数学教育学报，2016，25（3）：61-65．

[41] 李大永，章红．基于整体把握的运算主线下的“分数指数幂”教学[J]．数学教育学报，2016，25（1）：61-63．

[42] 方均斌，梁凯，朱玲．数学问题教学的五个探索点[J]．数学教育学报，2016，25（1）：47-50．

[43] 曹一鸣，王万松．高中概率统计内容设置的国际比较——基于15个国家数学课程标准的研究[J]．数学教育学报，2016，25（1）：1-4．

[44] 叶志强，张辉蓉．数学文化与职前小学教师教育[J]．数学教育学报，2016，25（3）：56-60．

[45] 吴骏，汪晓勤．初中数学教师HPM教学的个案研究[J]．数学教育学报，2016，25（1）：67-71．

[46] 韩继伟，黄毅英，林智中．初中数学教师的学科知识研究[J]．数学教育学报，2016，25（2）：49-54．

[责任编校：周学智]

Current Situation and Prospect of Mathematics “Four Basics”

ZENG Zheng1, YANG Yu-hui2, WU Jin-yan3

(1. Foshan University, Guangdong Foshan 528000, China;2. Hainan Normal University, Hainan Haikou 571158, China;3. The Third Primary School of QiongShan, Haikou City, Hainan Haikou 571100, China)

Mathematics “Four Basics” had been an important and hot point for Chinese mathematics education in current years, especially after the issue of “mathematics curricular standards for full compulsory education (2011)”, and related researches had become more abundant. 194 papers could be found in CNKI if we used mathematics “Four Basics” as key word. The mathematics “Four Basics” researches could be divided into four parts: the forming and development of mathematics “Four Basics”, the connotation of mathematics “Four Basics”, the relationship of mathematics “Four Basics”, and the teaching of mathematics “Four Basics”. The combing and analysis on those research results could be viewed as a reference for its further research.

mathematics “Four Basics”; combing; relation; teaching practice

G40-034

A

1004–9894（2017）02–0066–05

2017–02–21

天津市哲学社会科学规划（重点）项目——立德树人背景下中学生学科核心素养测评——以语数外为例（TJJX16-007）

曾峥（1961—），男，广东蕉岭人，教授，硕士研究生导师，主要从事不等式、数学教育研究．杨豫晖为本文通讯作者．