导数及其应用问题例析

导数及其应用问题例析

■河北省衡水市郑口中学 张志勇

导数的应用十分广泛,如求函数的单调区间、极值、最值,求曲线的切线以及解决某些实际问题等。利用导数可使复杂问题变得简单,导数为研究函数的单调性以及极值问题等提供了解题思路和方法,因而成为新高考的一个热点。高考对导数的要求主要表现在三个方面：①考查导数的概念、求导公式和求导法则;②导数的简单应用,包括求函数的极值,求函数的单调区间,证明函数的增减性等;③综合考查,常以应用问题或有关导数内容的综合问题出现。

一、导数的几何意义

导数的实质是函数值相对于自变量的变化率,体现在几何意义上就是切线的斜率。利用导数的几何意义,研究曲线的切线的斜率是导数的一个重要内容。求切线的方程可通过求导数先得到斜率,再由切点利用点斜式方程得到,求过点P(x0,y0)的切线方程时,一要注意P(x0,y0)是否在曲线上,二要注意该点可能是切点,也可能不是切点,因而所求的切线方程可能不止1条。已知曲线C：y=x3-3x2+2x,直线l：y=k x,并且l与C切于点(x0,y0) (x0≠0),求直线l的方程及切点坐标。解析：直线l过原点,知点(x0,y0)在曲线C上

则过点P(1,m)的切线斜率为k=f'(1)= -1-4a。

又切线方程为3x-y+b=0,故-1-4a= 3,即a=-1。

二、运用导数有关知识研究函数的单调性和最值(极值)问题

1.求函数单调区间的步骤为：①确定函数的定义域;②求导函数f'(x);③解不等式f'(x)＞0,得f(x)的递增区间;解不等式f'(x)＜0,得f(x)的递减区间,即函数的增区间是f'(x)≥0恒成立的区间,函数的减区间是f'(x)≤0恒成立的区间(导数值为零的点为有限个)。

利用求导方法讨论函数的单调性,要注意以下几方面：①在某个区间上f'(x)＞0是f(x)在该区间上递增的充分条件而非必要条件(f'(x)＜0亦是如此);②求单调区间时,首先要确定函数的定义域,然后再根据f'(x)＞0或f'(x)＜0,解出在定义域内相应的x的取值范围。设a∈R,已知函数(a x2+a+1)(e为自然对数的底数)。

令g(x)=-a x2+2a x-a-1。

①当a=0时,g(x)=-1＜0,f'(x)＜0,f(x)在R上为减函数。

②当a＞0时,方程g(x)=0的判别式Δ=4a2-4(a2+a)=-4a＜0,g(x)＜0,即f'(x)＜0,f(x)在R上为减函数。

③当a＜0时,由-a x2+2a x-a-1＞ 0,得

由-a x2+2a x-a-1＜0,得：

解析：f'(x)=x2-a x+(a-1)。当f'(x)=0,解得x1=1或x2=a-1。

当a-1≤1,即a≤2时,x∈(1,+∞)时,f'(x)＞0,所以f(x)在(1,+∞)内递增,不符合题意。

当a-1＞1,即a＞2时,x∈(1,a-1)时,f'(x)＜0;x∈(a-1,+∞)时,f'(x)＞0。

所以f(x)在(1,a-1)上递减;在(a-1,+∞)上递增。

又由已知得x∈(1,4)时,f'(x)＜0, x∈(6,+∞)时f'(x)＞0。

故4≤a-1≤6,即5≤a≤7。

2.求可导函数极值的步骤为：

①求导函数f'(x)。

②求方程f'(x)=0的根。

③检查f'(x)在方程根左、右的符号,如果左正右负,那么f(x)在这个根处取得极大值;如果左负右正,那么f(x)在这个根处取得极小值,如果左右不改变符号即都为正或都为负,那么f(x)在这个根处无极值。

设x=1与x=2是函数f(x)= al nx+b x2+x的两个极值点。

(1)试确定常数a和b的值;

(2)试分别判断x=1,x=2是函数f(x)的极大值点还是极小值点,并说明理由。

(1)由极值点的必要条件可知：f'(1)= f'(2)=0,即a0。解方程组可得

变式3：已知函数f(x)=a x3+b x2+ c x,取得极小值-4,并且使其导数f'(x)＞0的x的取值范围为(1,3),求f(x)的解析式。

解析：由题意得f'(x)=3a x2+2b x+ c=3a(x-1)(x-3),a＜0。

故在(-∞,1)上,f'(x)＜0;在(1,3)上, f'(x)＞0;在(3,+∞)上,f'(x)＜0。

因此,f(x)在x0=1处取得极小值-4。

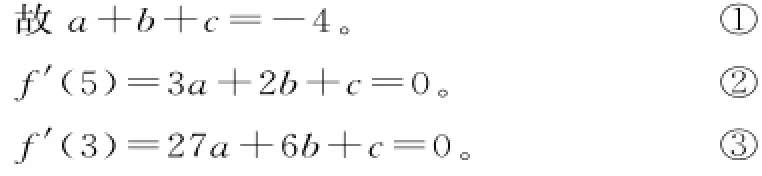
故f(x)=-x3+6x2-9x。

3.利用导数求函数的最值时,首先求f(x)在[a,b]内的极值,然后将f(x)的各极值与f(a)、f(b)比较得出函数f(x)在[a,b]上的最值。具体可分为以下几步：①求f'(x)=0的解x0;②用极值的方法确定极值;③将[a,b]内的极值与f(a),f(b)比较,其中最大的为最大值,最小的为最小值。

(1)当a=2时,求f(x)的极值;

(2)若不等式f(x)+3≥0对所有的实a数R恒成立,求a的取值范围。

由f'(x)=0得x=±1,当x变化时f'(x)及f(x)的变化情况如表1：对所有的实数R均成立,即

表1

令g'(x)=(x-1)(a x+2)eax=0,则时,g(x)取极大值x=1时,g(x)取极小值0,因而g(x)的最小值为

当

解得0＜a≤l n3。

变式4：已知函数f(x)=x3-a x2+3x。

(1)若f(x)在x∈[1,+∞)上是增函数,求实数a的取值范围;

(2)若x=3是f(x)的极值点,求f(x)在x∈[1,a]上的最小值和最大值。

解析：(1)f'(x)=3x2-2a x+3,要使f(x)在x∈[1,+∞)上是增函数,则有3x2-2a x+3≥0在x∈[1,+∞)上恒成立,即a内恒成立。

(2)由题意知f'(x)=3x2-2a x+3=0的一个根为x=3,可得a=5。

所以f'(x)=3x2-1 0x+3=0的根为

又f(1)=-1,f(3)=-9,f(5)=1 5,故f(x)在x∈[1,5]上的最小值是f(3)= -9,最大值是f(5)=1 5。

三、利用导数证明等式或不等式

利用导数证明等式或不等式为高中数学引进了新的思路和方法,在证明不等式或等式成立时,先要构造函数和确定其定义域,再运用求导的方法来证明。已知函数f(x)=al nx-a x-3,a∈R。

(1)讨论函数f(x)的单调性;

(2)若函数y=f(x)的图像在点(2, f(2))处的切线的倾斜角为4 5°,对于任意的t∈[1,2],若函数g(x)=x3+x2·在区间(t,3)上总不是单调函数,求实数m的取值范围;

(3)求证：l n(22+1)+l n(32+1)+ l n(42+1)+…+l n(n2+1)＜1+2 l nn!(n≥2,n∈N*)。

g'(x)=3x2+(m+4)x-2。

g'(0)=-2。

由题意知,对于任意的t∈[1,2],g'(t)

(3)令a=-1,此时f(x)=-l nx+x-3,所以f(1)=-2。

由(1)可知f(x)=-l nx+x-3在(1,+∞)上单调递增,故当x∈(1,+∞)时f(x)＞f(1),即-l nx+x-1＞0,l nx＜x-1对一切x∈(1,+∞)成立。

若n≥2,n∈N*,则有

因l n(22+1)+l n(32+1)+l n(42+1)+…+l n(n2+1)＜1+2 l nn!(n≥2,n∈N*),可变形为l nN*),所以：

变式5：已知函数f(x)=ex-l n(x+1) -1(x≥0)。

(1)求函数f(x)的最小值;

(2)若0≤y＜x,求证：ex-y-1＞l n(x+1)-l n(y+1)。

则函数f(x)在0,+∞[)上单调递增,函数f(x)的最小值为f(0)=0。

(2)由(1)知,当x＞0时,f(x)＞0。

因为x＞y,所以f(x-y)=ex-yl n(x-y+1)-1＞0。

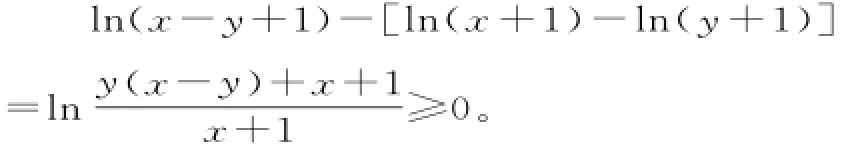
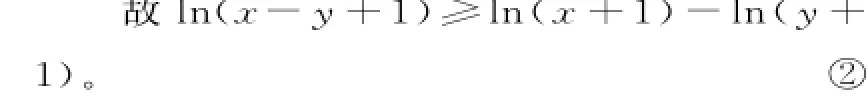
由①②可得：

ex-y-1＞l n(x+1)-l n(y+1)。

四、导数在实际问题中的运用

导数在自然科学、工程技术等方面都有广泛的应用,解决实际应用问题关键在于建立数学模型和目标函数,把“问题情景”译为数学语言,找出问题的主要关系,并把问题的主要关系近似化、形式化,抽象成数学问题,再归为常规问题,选择合适的数学方法求解。难点是如何把实际问题中所涉及的几个变量转化成函数关系式。烟囱向其周围地区散落烟尘而造成环境污染。已知A、B两座烟囱相距3k m,其中A烟囱喷出的烟尘量是B烟囱的8倍,经环境检测表明：落在地面某处的烟尘浓度与该处到烟囱距离的平方成反比,而与烟囱喷出的烟尘量成正比(比例系数为k)。若C是连接两烟囱的线段A B上的点(不包括端点),设A C=xk m,C点的烟尘浓度记为y。

(1)写出y关于x的函数表达式。

(2)是否存在这样的点C,使该点的烟尘浓度最低?若存在,求出A C的距离;若不存在,请说明理由。

解析：(1)设B处烟尘量为1,则A处烟尘量为8,故有A烟囱在C处的烟尘浓度为,B烟囱在C处的烟尘浓度为中0＜x＜3。

从而C处总的烟尘浓度为：

故当0＜x＜2时,y'＜0;当2＜x＜3时y'＞0。可见当x=2时,y取得极小值,且是最小值。

故在连接两座烟囱的线段A B上,距烟囱A处2k m处的烟尘浓度最低。

变式6：在甲、乙两个工厂,甲厂位于一直线河岸的岸边A处,乙厂与甲厂在河的同侧,乙厂位于离河岸4 0k m的B处,乙厂到河岸的垂足D与A相距5 0k m,两厂要在此岸边合建一个供水站C,从供水站到甲厂和乙厂的水管费用分别为每千米3a元和5a元,问供水站C建在岸边何处才能使水管费用最省。

设总的水管费用为f(θ),依题意有：

导数既是新课程的新增内容,又是函数、解析几何的交汇点,是同学们今后学习的基础,起着重要的工具作用,丰富了对函数研究的方法,现在已是新高考重点考查的基础知识,成为高考数学的一大热点,相信在今后的高考中仍然会重点考查,所以同学们一定要给予高度重视。

(责任编辑 徐利杰)