定积分的几类应用
定积分的几类应用
■江西省井冈山中学 贺 敬
定积分的应用是我们学习的重点内容,那么定积分究竟有哪些应用呢?下面我们进行归纳总结。
一、解决面积的求法
分析:可先画出图形,找出范围,用积分表示,再求积分值。
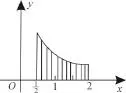
图1
点评:求平面图形的面积,首先要画出平面图形,然后根据图形的特点,选择相应的积分变量以确定积分区间,写出面积的积分表达式,再进行求解。
二、解决路程问题
一质点在直线上从时刻t=0(s)开始以速度v=t2-4t+3(m/s)运动,求:
(1)在t=4s的位移;
(2)在t=4s运动的路程。
分析:将区间[0,4]等分成n个小区间,在每个小区间[x,x+Δ x]上,当Δ x非常小时,可以近似看成匀速直线运动,当n无限大时,在t=4s位置就是v(t)在[0,4]上的定积分,而路程就是位移的绝对值之和。
解:(1)在时刻t=4s时,该点的位移为:
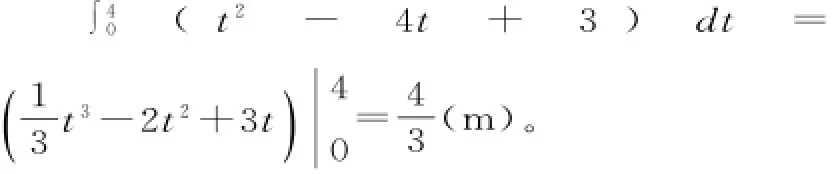
(2)v(t)=t2-4t+3=(t-1)(t-3),故在区间[0,1]及[3,4]上v(t)≥0,在区间[1, 3]上,v(t)≤0。
所以在t=4s时的路程为:

点评:由积分思想可知,做变速直线运动的物体所经过的位移,等于其速度函数v= v(t)在时间区间[a,b]上的定积分,而路程是位移的绝对值之和,故求路程要判断速度的符号。
三、解决变力做功问题
直径为2 0c m,高为8 0c m的圆柱体内充满压强为1 0N/c m2的蒸气,设温度保持不变,要使蒸气的体积缩小为原来的一半,则需要做的功是_____。

图2
分析:对变力F进行定积分,即可得变力所做的功。
解:设上端为活塞,且如图2所示取定x轴。另设底面面积为S,活塞压缩至x位置时气体的体积为V(x),压强为P(x),由于P V=k(其中k为常数),则:
故所做的功为:
点评:求变力做功问题,一般利用定积分加以解决,要注意寻找积分变量与积分区间。
(责任编辑 徐利杰)
- 中学生数理化(高中版.高二数学)的其它文章
- 有机化学专项训练(二)
- 解读烃和卤代烃知识考查热点
- 烃类易混淆点突破
- 烃类高考常见考点直击
- 电磁感应综合应用检测题
- 电磁感应新颖试题赏析

