构造函数解决极值点偏移问题
构造函数解决极值点偏移问题
■河南省虞城县高级中学 何海涛
已知连续函数f(x)在(x1,x2)内只有一个极值点x0且满足f(x1)=f(x2),若有则称函数f(x)极值点偏移。这种考题常位于于高考导数题的压轴位置,下面通过对这类题的分析,介绍如何利用构造函数的方法来解决极值点偏移问题。
一、高考题再现
(2 0 1 6年高考数学全国Ⅰ卷理科第2 1题) 已知函数f(x)=(x-2)ex+ a(x-1)2有两个零点。
(1)求a的取值范围;
(2)设x1,x2是f(x)的两个零点,证明:x1+x2<2。
解析:(1)f'(x)=(x-1)ex+2a(x-1)= (x-1)(ex+2a)。
①设a=0,则f(x)=(x-2)ex,f(x)只有一个零点。
②设a>0,当x∈(-∞,1)时,f'(x)<0,单调递减;当x∈(1,+∞)时,f'(x)>0,单调递增。
③设a<0,由f'(x)=0得x=1或x= l n(-2a)。
又当x≤1时,f(x)<0,所以f(x)不存在两个零点。
综上,a的取值范围为(0,+∞)。
(2)由x1,x2是f(x)的两个零点可得f(x1)=f(x2)=0,求证x1+x2<2等价于求证x1<2-x2。由于x1与2-x2的大小不容易比较,可以结合函数f(x)的单调性,转化为判断f(x1)与f(2-x2)的大小关系,考虑到f(x1)=f(x2),继而转化为判断f(x2)与f(2-x2)的大小关系,故可以构造函数F(x)=f(x)-f(2-x)。
不妨设x1<x2,由(1)知x1∈(-∞,1), x2∈(1,+∞)。
设F(x)=f(x)-f(2-x),则F'(x)= f'(x)+f'(2-x)=(x-1)(ex-e2-x)。
令F'(x)=0,则x=1。当x∈(-∞,1)时。F'(x)>0;当x∈(1,+∞)时,F'(x)>0。
故F(x)在R上单调递增。
因为x2>1,所以F(x2)>F(1)=0。
故f(x2)-f(2-x2)>0,f(x2)>f(2-x2)。
由x1,x2是f(x)的两个零点可得,f(x1) =f(x2)=0。
所以f(x1)>f(2-x2)。
因为x2∈(1,+∞),所以(2-x2)∈(-∞,1)。
又x1∈(-∞,1),y=f(x)在(-∞,1)上单调递减,所以x1<2-x2,即x1+x2<2。
点评:(1)本题第二问要求证明x1+x2<2等价于,不等式的左侧恰好是区间(x1,x2)中点的横坐标,常数1则恰好是函数f(x)的极值点,因此本题的本质是要证明极值点右偏的问题。
(2)构造函数F(x)=f(x)-f(2-x)是解决本题的关键,然后利用F(x)的单调性和零点及f(x1)=f(x2),将x1+x2<2转化化归为比较f(x1)与f(2-x2)的大小。
二、方法总结
若设f(x)的极值点为x0,则可将这类问题的求解方法总结如下:
(1)构造函数F(x)=f(x)-f(2x0-x)。
(2)对F(x)求导,判断F'(x)的正负号,确定F(x)的单调性。
(3)利用F(x0)=0,结合确定F(x)的单调性判断F(x)=f(x)-f(2x0-x)的正负,从而得到f(x)与f(2x0-x)的大小关系。
(4)若f(x2)>f(2x0-x2),结合f(x1)= f(x2),得到f(x1)>f(2x0-x2);
若f(x2)<f(2x0-x2),结合f(x1)= f(x2),得到f(x1)<f(2x0-x2)。
(5)结合函数f(x)的单调性,由f(x1)与f(2x0-x2)的大小关系,继而得出x1与2x0-x2的大小关系。
应用这一解题方法可以顺利解决函数极值点的偏移问题。
三、应用举例
(2 0 1 0年高考天津卷理科数学第2 1题)已知函数f(x)=xe-x(x∈R)。
(1)求函数f(x)的单调区间和极值;
(2)已知函数y=g(x)的图像与函数y=f(x)的图像关于直线x=1对称,证明当x>1时,f(x)>g(x);
(3)如果x1≠x2,且f(x1)=f(x2),证明x1+x2>2。
解析:(1)因为f(x)=xe-x(x∈R),所以f'(x)=(1-x)e-x,易知y=f(x)在(-∞, 1)上是增函数,在(1,+∞)上是减函数。
(2)由题意可知g(x)=f(2-x),因此, g(x)=(2-x)ex-2。
令F(x)=f(x)-g(x)=xe-x+(x-2)ex-2,于是F'(x)=(x-1)(e2x-2-1)e-x。
当x>1时,x-1>0,从而e2x-2-1>0。又e-x>0,所以F'(x)>0,从而函数F(x)在[1,+∞)上是增函数。
又F(1)=e-1-e-1=0,所以x>1时, F(x)>F(1)=0,即f(x)>g(x)。
(3)①若(x1-1)(x2-1)=0,由(1)及f(x1)=f(x2),则x1=x2=1,与x1≠x2矛盾。
②若(x1-1)(x2-1)>0,由(1)及f(x1)=f(x2),得x1=x2,与x1≠x2矛盾。
根据①②得(x1-1)(x2-1)<0,不妨设x1<1,x2>1。
由(2)可知,f(x2)>g(x2),因为g(x2)= f(2-x2),所以f(x2)>f(2-x2),从而f(x1)>f(2-x2)。
因为x2>1,所以2-x2<1。又由(1)可知函数y=f(x)在(-∞,1)上是增函数。所以x1>2-x2,即x1+x2>2。
点评:(1)本题第三问要求证明x1+x2>2等价于本题的本质是要证明极值点左偏的问题。
(2)在例1和例2中,通过构造函数y= f(x)与y=f(2-x)的差,从而得出f(x2)与f(2x0-x2)的大小关系,并通过转化进一步求证了x1+x2与2x0的大小关系。我们也可以构造F(x)=f(x0+x)-f(x0-x)来比较f(x2)与f(2x0-x2)的大小。
(2 0 1 1年高考辽宁卷理科第2 1题)已知函数f(x)=l nx-a x2+(2-a)x。
(1)讨论f(x)的单调性;
(2)设a>0,证明:当0<x<1 a时,

(3)若函数y=f(x)的图像与x轴交于A、B两点,线段A B中点的横坐标为x0,证明:f'(x0)<0。
解析:(1)f(x)的定义域为(0,+∞)。
①若a≤0,则f'(x)>0,f(x)在(0,+∞)上单调增加。
则g(x)=l n(1+a x)-l n(1-a x)-2a x。当0<x<时,g'(x)>0,而g(0)=0,所以g(x)>0。
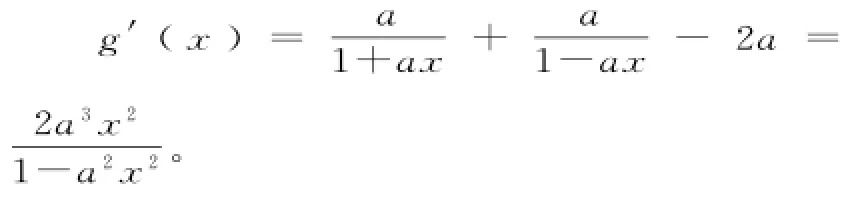
(3)由(1)可知,当a≤0时,函数y= f(x)的图像与x轴至多有一个交点,故a>0,从而f(x)的最大值为
不妨设A(x1,0),B(x2,0),0<x1<x2,则x1>0。
由(1)知,f'(x0)<0。
四、应用练习
函数f(x)=a x+b-xl nx的图像在(1,f(1))处的切线方程为y=x。
(1)求实数a,b的值;
(2)记f(x)的两个零点为x1,x2(x1≠x2),求证x1+x2>2 e。
解析:(1)由函数f(x)=a x+b-xl nx,得f'(x)=a-1-l nx。因为函数y=f(x)在x=1处的切线方程为y=x,所以
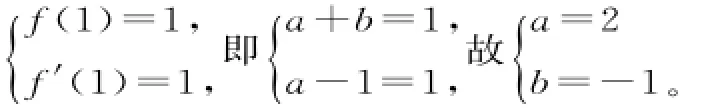
(2)由(1)知f(x)=2x-1-xl nx,所以f'(x)=1-l nx。
当x∈(0,e)时,f'(x)>0;当x∈(e,+∞)时,f'(x)<0,故f(x)在x=e处取得极大值。
不妨设0<x1<e<x2,令F(x)=f(x)-f(2 e-x)。
则F'(x)=2-l n(2 ex-x2)≥2-l ne2=0,F(x)在(0,+∞)上的增。
因为0<x1<e,所以F(x1)<F(e)=0,即f(x1)-f(2 e-x1)<0,f(x1)<f(2 ex1)。
因为f(x2)=f(x1)=0,所以f(x2)<f(2 e-x1)。
因为0<x1<e<x2,所以2 e-x1>e。
又当x∈(e,+∞)时,f(x)为减函数,所以x2>2 e-x1,即x1+x2>2 e。
(责任编辑 徐利杰)

- 中学生数理化(高中版.高二数学)的其它文章
- 有机化学专项训练(二)
- 解读烃和卤代烃知识考查热点
- 烃类易混淆点突破
- 烃类高考常见考点直击
- 电磁感应综合应用检测题
- 电磁感应新颖试题赏析

