波浪与带有窄缝结构作用的非线性数值模拟
宁德志,苏晓杰,滕 斌
(大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024)
波浪与带有窄缝结构作用的非线性数值模拟
宁德志,苏晓杰,滕 斌
(大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024)
针对波浪与带有窄缝结构作用产生的流体共振问题,采用基于域内源造波技术的时域高阶边界元方法并在窄缝内流体引入人工阻尼,建立了自由水面满足完全非线性边界条件的二维时域数值波浪水槽模型。求解中采用混合欧拉-拉格朗日方法追踪流体瞬时水面,运用四阶龙格库塔方法更新下一时间步的波面和速度势,利用加速度势的方法来求得作用结构上的瞬时波浪荷载。通过与已发表文献的数值与实验结果对比,验证了模型的准确性。同时通过大量的数值计算研究了共振条件入射波浪非线性对反射波高、透射波高和窄缝内波高、及结构波浪荷载和压力分布的影响。
窄缝;数值波浪水槽;流体共振;源造波技术;高阶边界元
0 引 言
在海洋工程结构作业过程中,经常会出现多浮体结构并排布置联合作业的情况,在浮体间会出现相对结构尺度小很多的窄缝。如由很多独立模块组成的超大型浮体,这些模块间存在窄缝;浮式生产储卸油系统(FPSO)与穿梭油轮并联进行油气外输时和大型船舶在码头前系泊时也都存在这种窄缝问题。窄缝内的水动力相互作用是十分复杂的水动力干涉问题,窄缝内水体在某些频率波浪作用下会发生共振现象,诱发很大的波浪爬高和荷载,进而对结构的作业安全带来很大的负面影响。
关于多结构间窄缝内水体共振问题,国内外学者已开展了很多研究探索其产生机理及相关的水动力相互作用问题等。譬如,Miao等[1]采用渐近匹配法研究了带狭缝二维双箱的共振现象,指出了共振频率与方箱的吃水深度和狭缝宽度的关系,并给出狭缝很小时双箱的理论共振频率。滕斌等[2]和何广华等[3]采用比例边界有限元方法分别研究了波浪与两箱和三箱结构作用下窄缝内水体共振现象。Saitoh等(2006)[4]和 Iwataet等(2007)[5]分别对不同入射波浪作用下两个方箱和三个方箱之间窄缝的波高变化进行了试验研究,发现窄缝内最大共振波高可以达到入射波高的五倍,共振频率与共振波高与箱体的吃水深度、窄缝宽度和箱体个数成一定的函数关系。Kristiansen和Faltinsen(2009)[6]对波浪与具有窄缝的二维箱体和固定式岸壁结构之间的相互作用开展了数值和试验模拟,发现线性和非线性势流数值结果都比共振条件下的窄缝内试验波高要大,尤其是线性结果更大。Kristiansen和Faltinsen(2010)[7]对波浪与具有窄缝的二维浮式箱体和固定岸壁式结构间的相互作用进行了数值和试验模拟,研究了共振条件下浮体三个自由度的运动响应与水动力系数。Lu等(2010,2011)[8-9]采用粘性流模型和改进的线性势流模型对结构间窄缝内水体共振问题进行了研究,发现在选取一定的人工阻尼系数条件下,线性势流模型也可以得到与试验和粘性流模型一样的结果。Li和Zhang(2016)[10]基于完全非线性势流理论采用边界元方法对两个做升沉运动方箱间窄缝内水体运动进行了模拟分析。Feng和Bai(2015)[11]采用基于入散射分离技术的完全非线性高阶边界元方法对两个三维方箱间窄缝内容水体共振运动进行了模拟。
在上述研究工作基础上,本文通过采用高阶边界元方法建立自由水面满足完全非线性边界条件的时域数值波浪水槽,采用域内源造波方法造波并布置前置阻尼层消除二次反射影响,进而可以在较短计算域内实现长时间模拟;在窄缝水体内引入常人工阻尼系数来近似共振条件下粘性耗散,进而求解波浪与具有窄缝两结构的相互作用问题。通过与Saitoh等[4]实验结果及Lu等[9]的CFD数值结果进行对比证明了本模型的准确性,并进一步通过大量数值计算研究了入射波浪非线性对反射波高、透射波高、窄缝内共振波高和波浪荷载等的影响,以及共振条件下结构各侧面的压力分布等。
1 数学模型
本文研究的波浪与具有窄缝的两方箱作用布置如图1所示,建立的笛卡尔坐标系Oxz,z=0位于静水面上,且z轴向上为正,x轴右方向为正。计算域包含自由水面Гf和固体边界ГN(包括水底Гd和箱体Гb)。波浪由控制垂直源造波面(Гs)的流量密度产生。图中h为水槽静水深,W为箱体宽度,D为箱体吃水深度,Wg为两箱体间窄缝的宽度,点I、II、III和IV分别代表箱体A和箱体B迎浪点和背浪点,而点Ⅴ是窄缝中间位置水面点。b、c、d、b0、c0、d0分别代表箱体A和箱体B的迎浪面、背浪面和底面。在流体无粘、不可压缩和流动无旋的假定下,整个流域的速度可用速度势的梯度来描述,上述问题的控制方程为由速度势满足的泊松(Poisson)方程[12-13],即

图1 水槽示意图Fig.1 Definition sketch of the wave flume

式中:q*(xs,z, t)=2vδ(x- xs)为造波源强度,造波位置x=xs(本文均取xs=0),v为流体质点水平速度,本文给定二阶Stokes速度解析解。
在自由水面上,满足完全非线性动力学和运动学边界条件,本文中采用混合欧拉-拉格朗日方法更新自由水面,利用物质导数d/d t=∂/∂t+v·▽,并在计算域的上游和下游区域的自由水面分别布置人工阻尼层来吸收从结构物反射回来的波浪与出流波浪[14],在窄缝内布置一常参数人工阻尼来近似由于涡和分流引起的粘性耗散,Kim(2003)[15]用此方法模拟了自振频率下容器内液体晃荡的粘性耗散。自由水面边界条件可以写成以下形式:

式中:η代表自由水面的铅垂位移,g是重力加速度,X0=(x0, )0 是指水质点静止时的位置,造波源位置为x=0,阻尼系数μ1用于计算域边界的两个阻尼层,阻尼系数μ2用于窄缝内自由水面,其数值根据试验粘性耗散来确定,L为阻尼层长度,本文取1.5倍波长,即1.5λ,k是波数,ω是波浪角频率,满足如下线性色散方程关系

在固定的结构表面和底面边界上,流体法向速度为0,满足固壁不可渗透边界条件,即:

假定自由水面初始时是静止的,即:

在整个流域内对速度势应用格林第二定理,可得到如下边界积分方程[14]:
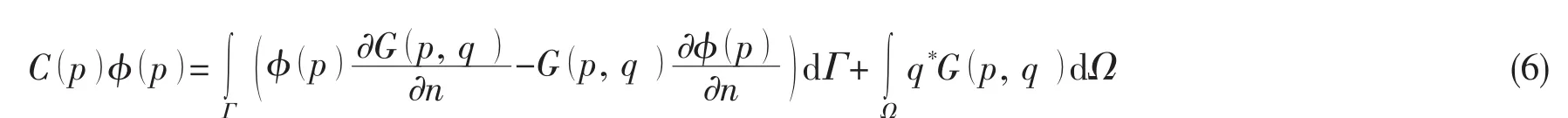
式中:p=(x0,z0)为源点,q=(x, z)为场点,C为固角系数,Ω代表整个流域,G是简单格林函数,考虑到水底镜像,可以表示为如下形式:

式中:r1为p和q两点距离,r2为p和q关于水底镜像之间距离。
本文用三节点高阶边界元离散计算域成一些曲线单元,单元内任一点的几何坐标和速度势等物理量可以用二次形状函数插值得到。积分方程经高阶边界元离散后,可通过求解线性方程组得到未知量。计算中认为当前时刻物面上的速度势法向导数和自由水面上的速度势是已知的,根据积分方程计算当前时刻物面上的速度势和自由水面上的速度势法向导数,然后应用四阶Runga-Kutta法,根据自由水面条件式(2)计算下一时刻的水质点位置和自由水面上的速度势,再用二次形状函数在旧单元上插值求得新节点上的物理量来对自由水面网格重新划分,重新应用积分方程计算下一时刻物面上的速度势和自由水面上的速度势法向导数。这样计算周而复始,直到计算结束[16-17]。
求解作用在结构上的波浪力F= {fx,fy}可通过在瞬时物体湿表面Гb上做压强积分得到
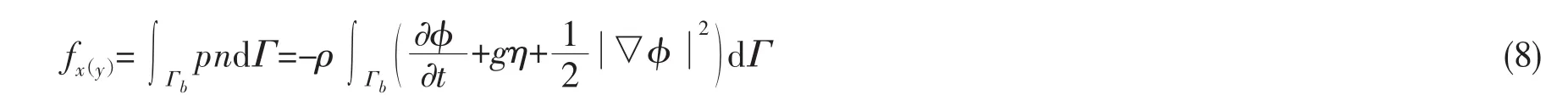
速度势的时间导数φt也满足Laplace方程

在自由水面Гf上,φt由Bernoulli方程给出:

在固定边界上满足

进而通过求解积分方程
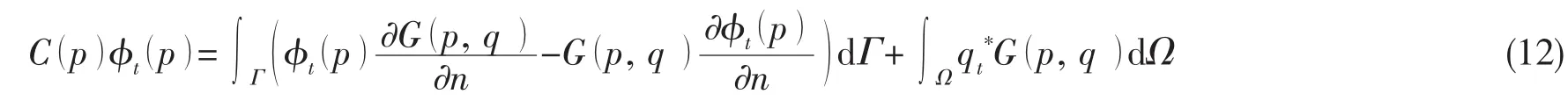
可以求得φt,其中系数矩阵与(6)式中相同,不用重新建立,qt*为源强qt的时间导数,可解析求得。最后通过(8)式求得作用在物体上的波浪力。
2 数值计算及讨论
2.1 模型准确性和稳定性
作为算例,本文以Saitoh等(2006)[6]的实验来进行数值模拟波浪与具有窄缝的两箱体的相互作用问题,验证本文数学模型的准确性。这里选用的实验参数为水槽静水深h=0.5m,箱体A和B的宽度W=0.5m,吃水深度D=0.252m,入射波高H0=0.024m,箱体间窄缝宽度Wg=0.03m、0.05m和0.07m。在数值模型中,计算域长度取7.5倍波长,在水槽的左右两端各布置1.5倍波长的阻尼层,造波源位于x=0,箱体A侧面边界b位于距离造波源2.5倍波长的位置,然后依次按Wg调整箱体B的位置。通过开展数值收敛性实验,自由水面上每个波长布置15个单元,窄缝内布置2个单元,箱体侧面边界b、d、b0、d0均布置6个单元,底面边界c和c0均布置12个单元;时间步长Δt=T/60 s,每个算例模拟30个周期。
图3给出了窄缝宽度Wg分别为0.03m、0.05m和0.07m情况下窄缝中心位置V点处无量纲波高Hg/H0随入射波波数kh的变化关系,及本文数值结果与实验数据[4]、粘性流模型数值结果[9]的比较。通过数值实验测算,窄缝中间水面的人工粘性系数分别取为μ2=0.04,0.03,0.03;数值模拟中,波高Hg以测试点的波面时间序列中波峰值与波谷值和的平均来计算。从图中可以看出,三种窄缝宽度情况下,窄缝内数值模拟波面高度分别在kh=1.7,1.58和1.47时达到最大,也即窄缝内流体发生共振,波高分别为入射波高的4.3倍、5.2倍和5.0倍。整体上两种数值结果与实验数据均符合得很好,在个别峰值处甚至本文结果比粘性流模型结果与实验数据吻合得更好,说明所建立模型在取得合适的人工粘性系数情况下可以准确模拟窄缝内流体共振问题。
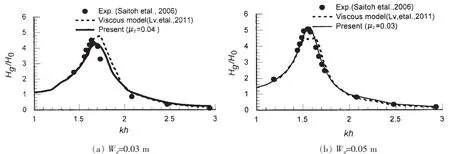

图2 窄缝中间位置V处无因次波高Hg/H0与波数kh间的关系Fig.2 Distribution of non-dimensionalwave heightwith respect to incidentwave frequency
图3给出了窄缝宽度Wg为0.05m时上述波况下作用在箱体A和B上的x和z向无量纲化波浪荷载幅值随波数kh的变化,及本文结果与粘性流模型[9]和线性势流模型[9]结果的对比,图中波浪荷载幅值以波浪力时间稳定段序列中峰值与相邻谷值和的一半的平均来计算。从图中可以看出,作用在两个箱体上的波浪荷载也均是在共振频率处达到最大,同时三种数值结果均吻合得很好,也进一步说明本模型可以准确模拟窄缝内共振流体作用在结构上的波浪荷载。

图3 窄缝宽度Wg为0.05m时作用在两箱体波浪荷载随波数的分布Fig.3 Distribution of dimensionlesswave forces on twin boxes against kh at Wg=0.05m
图4给出了波数kh=1.58,窄缝宽度Wg=0.05 m,入射波高H0=0.024 m情况下t=26T和30T时的整个计算域波面分布,图中波面空白处为两个箱体所在的位置。从图中可以看出,两个时刻的波面曲线已经完全重合,包括箱体A前的反射波,箱体B后的透射波和两个箱体之间的窄缝内波面;在水槽两端的阻尼层吸收波浪的效果都很理想,两端的波面基本趋于0,箱体A前的波浪形成了稳定的立波,说明其反射回去的波浪透过造波源被前端阻尼层完全吸收,而对入射波浪没有产生影响。以上现象说明本模型的模拟结果已达到稳定。图5给出了箱体A和B的水平荷载和垂向荷载的时间历程,从图中可以看出,水平力和垂向力在数值上均达到稳定,在共振条件下,窄缝内水体的作用占主导,其作用的侧面d和b0法向量相反,箱体A和B的水平力反相位;而作用在箱体A底面c上的反射浪非线性要强于作用在箱体B底面c0上的透射浪,导致了作用在箱体A和B的垂向力在相位和幅值上的差异。
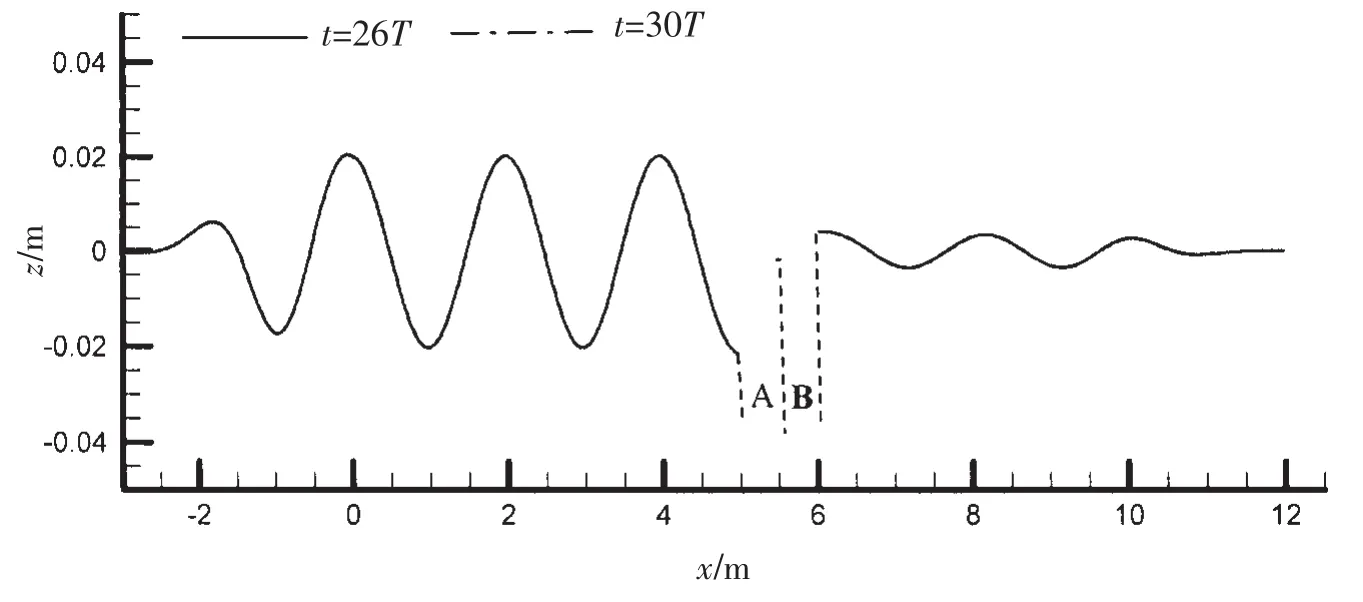
图4 t=26T和30T两个时刻的水槽波面分布Fig.4 Snapshotofwave elevation along the wave flume at t=26T and 30T

图5 箱体的水平和垂向荷载时间历程Fig.5 Time series ofwave loads on boxes in horizontal and vertical directions
2.2 数值结果
下面以上述算例中窄缝宽度Wg=0.05m为模拟对象,进一步分析入射波浪非线性对波浪爬高和荷载的影响,以及共振条件下压力分布等问题。图6给出了共振条件下(即,kh=1.58)入射波高H0分别为0.04m、0.06m和0.08m时窄缝内的波面分布情况,图中波面通过除以入射波幅(H0/2)进行无量纲化处理。计算中对窄缝内三点II、V、III的波面时间历程进行记录,通过对比发现三点波面历程完全相同,说明窄缝内流体没有发生x方向波动,而是沿着z向做整体波动,故而可以用窄缝内任一点代表整个流体波动情况。从图6可以看出,入射波高H0=0.08m对应的曲线无量纲化波高最大,传播速度最快,H0=0.04m对应的曲线无量纲化波高最小,传播速度最慢,这说明了大波高入射波浪所体现的强非线性作用。
图7为入射波高H0=0.024 m时结构迎浪侧(I点)、背浪侧(IV点)和窄缝内(V点)的无量纲化波高Hg/H0随入射波数kh的变化关系。从图中可以看出,在共振频率处kh=1.58,窄缝内V点和背浪侧IV点波高均达到最大,而迎浪侧I点则为最小,这是因为当窄缝内共振时能量达到最大,同时会分别有一部分能量向迎浪侧和背浪侧传递,与迎浪侧波浪能量作用起到减弱效果,而与背浪侧波浪能量作用起到增强的效果。在高频区域,窄缝内波浪和背浪侧波浪都趋于很小值,而迎浪侧波高Hg/H0趋于常值2,这是因为对应短波大多被结构迎浪面全反射,进入到窄缝和背浪侧的波浪成分很少的缘故。
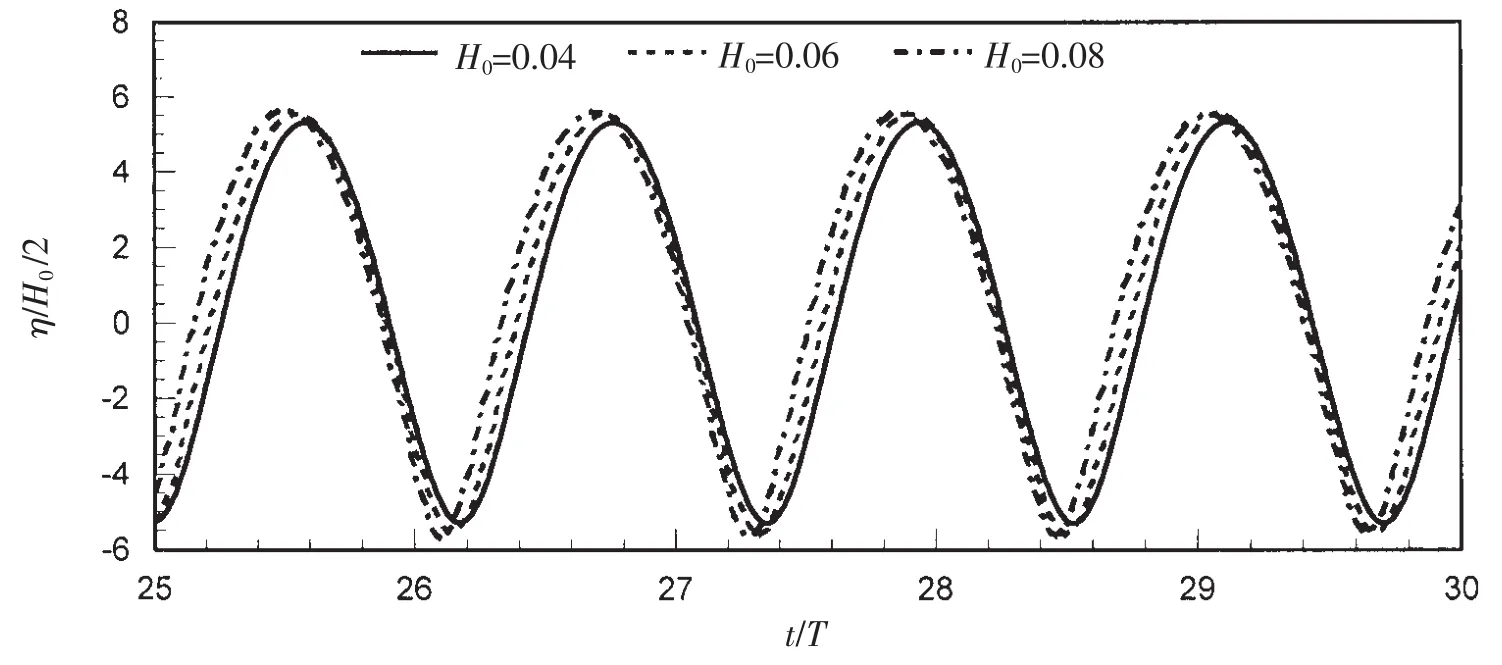
图6 共振条件不同入射波幅对应的窄缝内波面时间历程Fig.6 Time series ofwave elevation atnarrow gap for different inputwave amplitude at resonance

图7 不同位置无因次波高与入射波频率的关系Fig.7 Dimensionlesswave height against kh at different positions
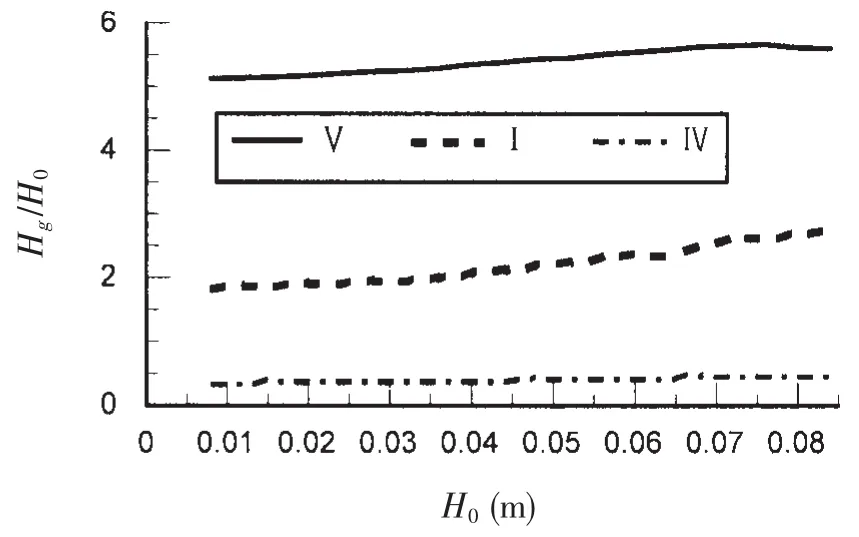
图8 共振时不同位置无因次波高与入射波波高的关系Fig.8 Dimensionlesswave heightagainst H0at different positions at resonance
图8为共振条件下kh=1.58,迎浪侧(I点)、背浪侧(IV点)和窄缝内(V点)的无量纲化波高Hg/H0随入射波高H0的变化关系。从图中可以看出,在H0≤0.03 m时,三条曲线均近似为水平线,表现为波浪的线性特性;反之,波高Hg/H0均随着入射波高H0的增加而增大,呈现为波浪的非线性特性,在H0= 0.08 m时,Hg/H0在I点、IV点和V点的值分别达到2.7、5.6和0.46,而在H0=0.01m时,三点处波高仅为入射波高的1.85倍、5.1倍和0.34倍。

图9 共振条件下箱体A和B的无因次波浪荷载随入射波高的变化关系Fig.9 Dimensionlesswave loads on boxes A and B against H0at resonance
图9是共振条件下kh=1.58,箱体A和B的无因次化水平荷载与垂向荷载随入射波高H0的变化关系。从图中可以看出,当H0≥0.03m,作用在两个箱体上的波浪荷载如波高变化一样呈非线性特性,且总体上作用在迎浪侧箱体A的荷载要大于背浪侧的箱体B,这与透射到箱体后的波浪贡献很小相关。从图9(a)中还可以发现,当H0≥0.07m,作用在箱体A上的水平荷载开始减小,而作用在箱体B上的水平荷载一直处于增大趋势,分析其原因是入射波高增大,波浪非线性增强,高阶波浪贡献相应增大,而根据立波理论,作用在迎浪侧b上的偶数阶(尤其是二阶差频项)波浪荷载的相位与线性部分呈反相位,使得箱体A整体波浪荷载下移。
图10是共振条件下kh=1.58,箱体A和B各个侧面上的最大波压力空间分布,其中图10(a)中的横坐标x=0分别代表两个箱体在窄缝内的下端点。从图10(a)中可以看出,由于受窄缝内共振波浪的影响,两箱体内侧压力最大且相当,随着向箱体外侧延伸,底面压力开始减小,由于透射波浪最小,所以箱体B上的压力减小最快,而在箱体A的外侧边缘位置,由于其立波的形成,使得该位置压力又开始增大。从图10(b)中可以看出,由于窄缝内发生共振,产生很大的水体垂向运动,所以作用在侧面d和b0上的压力是相同的,同时也是各个侧面中最占优的,而由于透射浪成分很小,作用在箱体B背浪面d0上的压力最小。

图10 窄幅共振条件下箱体底面和侧面最大波压力分布Fig.10 Distribution ofmaximum pressure along bottom and lateral sides of boxes at resonance
3 结 论
本文基于域内源造波的时域高阶边界元方法建立波浪与具有窄缝的两箱体结构相互作用的完全非线性数值水槽模型,对窄缝内流体共振条件下反射波高、透射波高、窄缝内波高、作用在箱体上的波浪荷载和各侧面上的最大压力分布等进行了模拟研究。通过与已发表实验数据和数值结果进行对比验证,表明本文所建立数学模型可以准确模拟波浪与具有窄缝结构相互作用过程,且在较小计算域内可长时间模拟得到稳定的结果,没有在入射边界发生二次反射现象。研究发现,窄缝内水体发生共振时,透射波高和窄缝内波高均达到最大,而反射波高则为最小;入射波高H0=0.08m时的反射波高、窄缝内共振波高和透射波高分别比H0=0.01m时增大0.41倍、0.1倍和0.35倍,说明箱体迎浪侧非线性最强,窄缝内流体非线性最弱;作用在箱体上的波浪荷载非线性影响明显,整体上为作用在迎浪侧结构上的荷载大于背浪侧结构,但当入射波浪非线性增大到一定程度时,由于立波作用引起高阶波浪力的相位与线性部分相反,会使得作用在迎浪侧上的整体水平力会小于作用在背浪侧的结构;共振时,作用在窄缝内侧面上的波压力最大,而作用在迎浪侧结构底面上的波压力则呈现两端大中间小的特点。本研究还可以进一步拓展到波浪与具有窄缝的多结构相互作用、波浪与具有窄缝的船舶和码头之间的相互作用等问题,进而为海洋工程作业安全和设计提供参考和依据。
参 考 文 献:
[1]Miao G P,Ishida H,Saitoh T.Influence of gaps between multiple floating bodies on wave forces[J].China Ocean Engineering,2000,14(4):407-422.
[2]滕 斌,何广华,李博宁,程 亮.应用比例边界有限元法求解狭缝对双箱水动力的影响[J].海洋工程,2006,24(2):29-37. Teng B,He G H,Li B N,Cheng L.Research on the hydrodynamic influence from the gap between twin caissons by a scaled boundary finite elementmethod[J].Ocean Engineering,2006,24(2):29-37.
[3]何广华,滕 斌,李博宁,程 亮.应用比例边界有限元法研究波浪与带狭缝三箱作用的共振现象[J].水动力学研究与进展A辑,2006,21(3):418-424. He G H,Teng B,Li BN,Cheng L.Research on the hydrodynamic influence from the gaps between three identical boxes by a scaled boundary finite elementmethod[J].Journal of Hydrodynamics,Ser.A,2006,21(3):418-424.
[4]Saitoh T,Miao G P,Ishida H.Theoretical analysis on appearance condition of fluid resonance in a narrow gap between twomodules of very large floating structure[C]//Proceedings of the Third Asia-Pacific Workshop on Marine Hydrodynamics.Shanghai,China,2006,170-175.
[5]Iwata H,Saitoh T and Miao G P.Fluid resonance in narrow gaps of very large floating structure composed of rectangular modules[C]//Proceedings of the Fourth International Conference on Asian and Pacific Coasts.Nanjing,China,2007,815-826.
[6]Kristiansen T,Faltinsen O M.Studies on resonantwatermotion between a ship and a fixed terminal in shallow water[J]. Journal of Offshore Mechanics and Arctic Engineering,2009,131:021102
[7]Kristiansen T,Faltinsen OM.A two-dimensional numerical and experimental study of resonant coupled ship and pistonmodemotion[J].Applied Ocean Research,2010,32:158-176.
[8]Lu L,Cheng L,Teng B,Zhao M.Numerical investigation of fluid resonance in two narrow gaps of three identical rectangular structures[J].Applied Ocean Research,2010,32(2):177-190.
[9]Lu L,Teng B,Cheng L,Sun L,Chen X B.Modelling ofmulti-bodies in close proximity under water waves-fluid resonance in narrow gaps[J].Science China Physics,Mechanics&Astronomy,2011,54(1):16-25.
[10]Li L,Zhang C.Analysis of wave resonance in gap between two heaving barges[J].Ocean Engineering,2016,117:210-220.
[11]Feng X,BaiW.Wave resonances in a narrow gap between two barges using fully nonlinear numerical simulation[J].Applied Ocean Research,2015,50:119-129.
[12]Brorsen M,Larsen J.Source generation of nonlinear gravity waveswith the boundary integral equationmethod[J].Coastal Engineering,1987,11:93-113.
[13]Ning D Z,Teng B,Eatoack Taylor R,Zang J.Numerical simulation of non-linear regular and focused waves in an infinite water-depth[J].Ocean Engineering,2008,35(8-9):887-899.
[14]Tanizawa K.Long time fully nonlinear simulation of floating bodymotionswith artificial damping zone[J].The Society of Naval Architects of Japan,1996,180:311-319.
[15]Kim YW.Artificial damping in water wave problems I:Constant damping[J].International Journal of Offshore and Polar Engineering,2003,13(2):88-93.
[16]周斌珍,宁德志,滕 斌.造波板运动造波实时模拟[J].水动力学研究与进展A辑,2009,24(4):1-12. Zhou B Z,Ning D Z,Teng B.Real-time simulation of waves generated by a wavemaker[J].Journal of Hydrodynamics, Ser.A,2009,24(4):1-12.
[17]陈丽芬,宁德志,滕 斌,宋伟华.潜堤上波流传播的完全非线性数值模拟[J].力学学报,2011,43(5):834-843. Chen L F,Ning D Z,Teng B,Song W H.Fully nonlinear numerical simulation for wave-current propagation over a submerged bar[J].Chinese Journal of Theoretical and Applied Mechanics,2011,43(5):834-843.
Nonlinear numerical simulation of wave action on objectsw ith narrow gap
NING De-zhi,SU Xiao-jie,TENG Bin
(State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian 116024,China)
Based on a time-domain higher-order boundary elementmethod(HOBEM)with wave generation by the inner-domain source,a two-dimensional time-domain numericalwave flume is developed to investigate the fluid resonance due to the interaction between wave and objectswith a narrow gap.In the numericalmodel,the artificial damping is introduced into the fluid at gap and the fully nonlinear boundary conditions are satisfied on the instantaneous free surface.In the solving process,themixed Eulerian-Lagrangianmethod is adopted to track the transientwater surface and the 4th Runga-Kutta technique is used to refresh the velocity potential and free surface at the next time step.The acceleration potential technique is adopted to calculate the transientwave loads along the wetted object surface.By comparison with the published experimental and numerical data,the proposed model is validated.Numerical experiments are performed to study the effects of the incidentwave nonlinearity on reflection wave height,transmission wave height,wave height at narrow gap,wave loads and pressure distribution at resonance.
narrow gap;numericalwave flume;fluid resonance;source generation technique; higher-order boundary element
O353.2
:Adoi:10.3969/j.issn.1007-7294.2017.02.003
2016-07-20
国家自然科学基金资助项目(51679036,51490672);教育部新世纪优秀人才支持计划(NCET-13-0076);中央高校基本科研业务费专项资金(DUT14YQ206)
宁德志(1975-),男,教授,博士生导师,E-mail:dzning@dlut.edu.cn;
苏晓杰(1989-),男,博士研究生,E-mail:676413719@qq.com。
1007-7294(2017)02-0143-09

