将数学思想渗透在课堂教学中

康登辉

[摘 要]数学的课堂教学离不开数学思想的渗透，数学思想的渗透需要以数学知识为载体。教师应注重让学生在具体数学知识的获得和感悟数学思想。

[关键词]数学思想；数形结合；转化；建模

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2017）11-0087-01

数学课程标准指出：“通过义务教育阶段的数学学习，学生能获得适应社会生活和进一步发展所必需的数学基础知识、基本技能、基本思想、基本活动经验。”但是在学生的数学学习过程中，教师往往过分关注学生对知识的掌握情况及掌握的熟练程度，忽略学生获得知识的过程以及在这个过程中的数学思想的渗透。日本数学教育家米山国藏指出：“作为知识的数学出校门不到两年就忘了，唯有深深铭记在头脑中的数学精神、数学思想、研究的方法和着眼点等，这些随时随地发生作用，使人终身受益。”因此，教师在注重知识获得的同时，还应注重思想方法的渗透，让学生习得终身受益的思想方法。

一、巧用数形结合，促进知识框架的建构

数学家华罗庚先生说：“数缺形时少直观，形少数时难入微。”例如，教学“表内乘法”时，乘法的概念是学生学习的重点和难点。在教学中，教师首先出示一幅动物场景图，引导学生观察并说一说从图中发现了什么。学生在观察和交流中形成了丰富的感性认识，当教师抛出“兔子有多少只？鸡有多少只？”的问题时，学生很肯定地说应把“几个几相加”，在学生建立丰富的“形”的表象后，教师顺势指出几个数相加可用乘法计算。

借助“形”的呈现，促进学生对乘法意义的理解。数与形的有效结合，促进了学生对乘法含义的内在建构，在意义的建构过程中，学生初步感受到了朦胧的数形结合思想，促进了学生数学思想的积累，有效提升了学生解决问题的能力。

二、妙用转化思想，促进数学思想的形成

数学知识具有一定的逻辑关系，可借助旧知展开对新知的学习。例如，教学“分数乘整数”时，学生对同分母分数加法及整数乘法已经有了清晰的认识，课始，教师引导学生复习相关知识后，出示例题：“做一朵花需绸带3/10米，做3朵花需绸带多少米？”学生联系旧知，自然会想到：3个3/10是多少？在独立探索计算方法的环节中，学生借助同分母分数相加的计算方法及分数乘整数的意义，很顺利地得出了3×3/10。在师生互动交流环节中，学生围绕3×3/10计算方法的探索过程展开交流，最终得出“3个3/10相加，分母不变，分子相加，分子是3个3相加，可以用3×3”表示的结论，即分母不变，分子与整数相乘。

通过交流，学生借助旧知推出新知，推理过程中突出了转化思想，促进了学习方法的掌握，有效促进数学学习能力的提升。

三、运用建模思想，促进知识模型的建构

低年级学生的思维处于形象阶段，对数学知识的理解往往需要借助“拐杖”，即将抽象的知识形象化，才能完成知识的建构。

例如，教学“9加几”时，教师一开始有序地呈现了“10+1，10+2，10+3，10+4，10+5，10+6，10+7，10+8，10+9”等题目，组织学生讨论：“通过刚才的计算，你发现了什么？”通过交流，学生发现： 10加几就是十几。接着教师出示题目：一盘9个桃，一盘4个苹果，一共有多少个水果？学生思考后列出算式“9+4”，然后教师引导学生思考：“算式的结果是多少？你是怎样计算的？”

生1：我看着图形一个一个地数，共有13个。

生2：我先把9记在心里，然后往后再数4个数，一共是13个。

生3：我根據桃子和苹果的数量，在本子上画出相应数量的圆圈，再数圆圈的数量，共有13个。

生4：因为10加几等于十几，4可以分成1和3，先从4里拿出1与9合成10，再算 10+3=13，所以共有13个。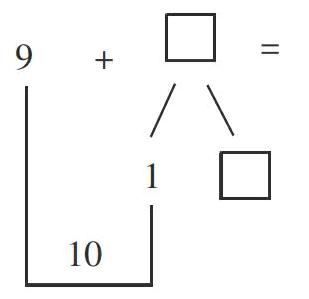

教师根据学生的回答，组织学生进行讨论：“你喜欢哪一种解题方法？为什么？”学生各抒己见，最后得出结论：先凑成10，再加上余下的数，这样不但快，而且不容易出错。在学生重复“凑十”的思想时，教师在黑板上板书（如右图所示）。

模型的建立符合一年级学生的形象思维特征，降低了学生的思考难度。出示题目“9+7”时，学生的思路很清晰：7=1+6，9+1=10 ，10+6=16。反复的练习与反思，使学生在交流解题方法的过程中明确“凑十”的数学思想，并很快掌握了这类计算方法。教师再出示题目“8+6”，学生稍作迁移，就能得出“8+2+4”的思路。

总之，教师在教学中应适时渗透数学思想方法，让学生在潜移默化中受到数学思想熏陶，有效促进学生数学思维能力的发展，真正提高学生的数学素养，使之终身受益。

（责编 韦 迪）