变截面加筋板尺寸-布局一体化设计
王 博,田 阔,郝 鹏,郑岩冰,赵海心,王捷冰
(1.大连理工大学 工程力学系 工业装备结构分析国家重点实验室,大连 116024;2.空间物理重点实验室,北京 100076)
变截面加筋板尺寸-布局一体化设计
王 博1,田 阔1,郝 鹏1,郑岩冰1,赵海心1,王捷冰2
(1.大连理工大学 工程力学系 工业装备结构分析国家重点实验室,大连 116024;2.空间物理重点实验室,北京 100076)
为了提高加筋板结构的开口补强效率,文中提出了一种新型变截面加筋构型。通过丰富加筋结构层级,有效抑制了开口引发的失稳变形扩展,从而提高了结构的承载能力。在优化设计中,为了合理缩减设计变量的数目,文章采用函数变量来分别描述加筋层级与布局的变化规律。进而基于代理模型,实现了尺寸-布局一体化设计。最后,与等尺寸、等布局优化方法及等布局、尺寸余弦分布的优化方法的结果进行对比,凸显了文中所提出的一体化设计方法的简洁与有效。
多级加筋板;开口补强;极限承载力;一体化设计
0 引言
为满足设备安装、管线铺设、散热等功能型需求,开口不可避免地出现在火箭仪器舱、导弹级间段和飞机机身等航空航天加筋结构中[1-2]。开口引起了加筋板的局部刚度折减,导致开口处过早发生局部失稳,进而扩展至结构整体失效[3]。为了有效提高开口加筋板的承载能力,亟需提出新颖而高效的开口补强方法。Shi等[4]面向轴压复合材料加筋柱壳结构,从抵抗开口附近失稳的角度提出了多种局部加筋补强构型。Dang等[5]、Hao等[3,6]在开口加筋平板、曲板及圆柱壳中,采用曲线加筋替代直筋,自适应地增大了补强的优化空间。
近年来,受到巨型土木建筑[7]及生物力学[8]中蕴含的层级理念的启发,学者们提出了具备高承载能力的多级加筋结构形式[9-11]。传统的单一层级的加筋结构具有一致的筋条形貌,而多级加筋结构在不同层级间具有明显的几何或材料差异,形成变截面特征。由于结构层级的丰富,多级加筋结构对局部几何缺陷[12]、裂纹扩展[13]等所引起的局部刚度衰减表现出优异的容忍性,有利于保持较高的结构承载力。尽管层级增多带来的增益很大,但现有的多级加筋结构的研究工作中筋条大多不超过2个层级[9-14],这是因为随着结构层级的增多,设计变量的数目也将激增,给优化设计带来巨大困难[15]。为了有效表征此类多层级加筋结构的变截面信息,Khvyiuzov等[16]和Quinn等[17]分别采用正弦和余弦函数来描述不同层级间的筋条高度分布。
为了提高加筋板优化设计的效率,冯玉龙等[18]提出了并行子空间法来对复合材料加筋板进行布局与尺寸优化。荣晓敏等[19]基于进化神经网络方法建立了复合材料格栅加筋板的代理模型,有效提高了结构优化效率。Wang等[20]针对非均匀轴压工况下的网格加筋壳,提出了加筋布局函数,合理减少了布局优化的变量数目。在此基础上,Hao等[3,6]建立了曲线加筋的布局函数。
本文首先针对轴压工况下的加筋板结构,研究了开口对结构承载能力的折减效应及对失稳模式的影响;进而提出了简洁的变量函数来分别描述变截面加筋层级与布局的变化规律,建立了基于代理模型的优化框架,并开展了以最大化结构承载力为目标的尺寸-布局一体化设计;最后与传统的等尺寸-布局、等布局、尺寸余弦分布的补强方法的优化结果进行对比。
1 开口加筋板承载能力分析
1.1 开口加筋板模型
本文以文献[9]中的典型加筋板作为算例,研究开口对加筋板承载能力的折减效应及失稳模式的改变。加筋板结构示意图如图1(a)和(b)所示。加筋板蒙皮长度Lm=480 mm,宽度bm=360 mm,厚度tm=2 mm。共有9根加筋条,其高度hr=12 mm,厚度tr=4 mm,筋条间的间距br1=40 mm,蒙皮侧边与邻近的筋条距离br2=20 mm。模型材料属性:弹性模量E=72 000 MPa,泊松比为ν=0.31,密度ρ=2.8×10-6kg/mm3,屈服强度363 MPa,强度极限为463 MPa,延伸率为12%。本文在此完美加筋板模型的中部增加一个长圆形开口,这种开口形式在航空航天、船舶工程中普遍存在[21-22],相应的开口尺寸参数如图1(c)和(d)所示,其中Lc=80 mm,Rc=60 mm。
1.2 开口加筋板承载能力分析
与文献[9]一致,本文基于有限元软件ABAQUS显式动力学方法的准静态求解技术来准确地模拟结构后屈曲行为,进而得到结构极限承载力。基于四节点壳体减缩积分单元S4R对加筋板模型进行离散,其对于薄壳和厚壳均具有很好的适用性[23]。通过网格收敛性分析确定模型的单元尺寸为5 mm,且筋条高度方向划分两层单元。模型边界条件及加载条件如下:侧边自由,底端固支,顶端约束除轴向位移外的其余自由度,并将顶端面所有节点刚性耦合至参考点,在参考点上施加轴压位移载荷直至结构发生失稳破坏。对模型加载时间进行收敛性分析,确定显式动力学分析的加载时间为200 ms,加载总位移为2 mm。图2为计算得出的完美加筋板与开口加筋板位移-载荷曲线及其变形云图,其中完美加筋板与含开口加筋板极限承载力分别为165.9 kN和 123.4 kN。由于开口的存在,结构承载力降低了 25.6%。可看出,完美加筋板失稳波形主要集中在结构中部,并随着位移的不断加载而扩展至结构整体;而含开口加筋板失稳波形率先发生在开口周围的蒙皮处,使得局部区域更容易发生屈曲变形,导致结构刚度迅速折减,过早地发生整体失效。
2 开口加筋板尺寸-布局一体化设计框架
2.1 加筋板尺寸-布局函数
针对开口所引起的加筋板刚度折减,罗楚养等[21]指出合理的加筋优化是一种有效的补强方法。需要指出的是,为保证结构关于X轴的对称性,第0号筋条位置被固定,且左右两侧筋条的尺寸和布局均关于X轴对称。本文定义单侧筋条数目为n个,则加筋板筋条总数N=2n+1,为后文表述的清晰,本文以单侧筋条数目n作为设计变量,相应的筋条标号如图1所示。同时,为了防止侧边屈曲的发生,在优化中须固定靠近边界处的第n号筋条的位置。由此可见,本文以图1(b)所示的Ld区域作为设计区域(Ld=bm/2-br2),可优化设计的变量为第0~n号筋条的高度、第1~(n-1)号筋条的布局、筋条的厚度(所有筋条具有统一厚度)。
若所有的尺寸-布局变量都是独立的,则总计有(2n+1)个设计变量。当单侧筋条数目n增多时,上述设计变量数目也将激增,这极大地制约了优化效率。若采用等尺寸-布局设计,则变量数目降至3个,仅包括单侧筋条数目n、筋条统一高度hr和厚度tr。虽然减少了设计变量数目,但这样的设计人为地缩小了设计空间,很难自适应地补强开口所引起的局部刚度折减,易导致较低的补强效率。为了减少用来表征变截面加筋尺寸的变量数目,Quinn[17]等采用余弦函数来描述不同层级间的筋条高度分布,如式(1)所示。其中,Li代表第i号筋条距离第0号筋条(对称中心)的间距,hi代表第i号筋条的筋高,hα和hβ分布代表第0号和第n号筋条的筋高。由图3可看出,当hα=hβ时,筋条等高度;当hα
(1)
为了更有效地实现尺寸与布局的一体化设计,本文以2个变量函数λ1和λ2来分别表征布局和尺寸变量,以期合理减少设计变量的数目。第i号筋条的间距Li和筋高hi的表达式如式(2)所示。变截面加筋板的所有布局-尺寸变量可由布局和尺寸变量λ1和λ2、单侧筋条数目n、筋条厚度tr和第n号筋条的筋高hn这5个变量表示,表述简捷清晰。
i=0,1,…,n
(2)
图4更直观地表现了变量函数λ1和λ2的效果。当λ1= 1时,筋条等间距布局;当λ1< 1时,筋条关于对称中心X轴分布稀疏而在两端分布密集;当λ1> 1时,筋条关于对称中心X轴分布密集而在两端分布稀疏;当λ2= 1时,筋条等高度;当λ2< 1时,筋条高度关于对称中心X轴递减;当λ2> 1时,筋条高度关于对称中心X轴递增。
2.2 径向基函数(RBF)代理模型
加筋板的后屈曲分析过程非线性程度较高且分析耗时较大,RBF模型被认为是处理此类问题非常有效、可靠的方法。RBF模型是一类以待测点与样本点间的欧氏距离为自变量的函数为基函数,进而通过线性加权的方式构造出来的代理模型,可把一个多维问题转化成为以欧氏距离为自变量的一维问题,其基本表达形式如下[24]:
φ(r)
(3)
r=‖x-xj‖
(4)
式中R(x)为预测值;λj为权系数;x为设计变量矢量;xj为第j个样本点上的设计变量矢量;r为第j个样本点与待测点间的欧氏距离;φ为基函数;n为样本点数量,其网络结构图如图5所示。
基于此模型,可建立起加筋板结构尺寸参数等输入量与结构承载力及质量等输出量之间的近似拟合关系,后续的优化设计可基于此代理模型开展。
2.3 开口加筋板尺寸-布局一体化设计框架
依据上述变量函数,本文提出了基于代理模型的开口加筋板尺寸-布局一体化设计框架,如图6所示。其框架流程如下:
(1)根据变量函数λ1和λ2,建立变截面加筋板有限元模型。
(2)基于最优拉丁超立方法[25]在设计空间抽取样本点,建立径向基函数(RBF)代理模型后,再另外抽取样本点进行误差评估,得到均方根误差(Root Mean Square Error,RMSE)、平均百分误差(Percent Average Error, AvgErr)、最大百分误差(Percent Maximum Error, MaxErr)3个误差表征结果[3]。其值越小,表示代理模型的拟合精度越高[26]。如果误差指标在可接受范围内,则接受所创建的代理模型,否则重新构建[27]。
(3)基于代理模型进行内层优化,选取多岛遗传方法作为优化算法。
(4)内层优化收敛后,调用一次精细模型分析来验证代理模型最优解的准确性。如果预测误差在0.5%以内则优化结束;如果精度不满足则将最优解的精细模型结果添加到初始代理模型中,生成新的代理模型,实施外层更新,再进行第三步,循环迭代,直至外层更新精度收敛,优化结束。
3 开口加筋板优化算例
基于本文提出的一体化设计框架开展优化设计,以λ1、λ2、n、tr和hn作为设计变量,以结构质量W不超过初始质量1.36 kg作为约束条件,以最大化结构极限承载力Pco作为优化目标,相应的优化空间如表1所示。同时,本文以等尺寸-布局优化[28]和等布局、尺寸余弦分布的优化[17]作为对比算例。等尺寸-布局优化的设计变量中单侧筋条数目n和筋条厚度tr的取值范围与一体化设计保持一致。筋条高度变量hr的上下限范围可根据一体化设计中hn、n、λ1和λ2的上下限取值来确定,如式(5)所示。这样的设置确保了2种优化方案的可对比性,等尺寸-布局优化空间如表2所示。等布局、尺寸余弦分布的优化中4个设计变量n、hα、hβ和tr的取值范围均与等尺寸-布局优化保持一致,其优化空间如表3所示。为了表述方便,分别命名上述尺寸-布局一体化设计、等尺寸-布局优化和等布局、尺寸余弦分布优化为优化1、优化2和优化3。
(5)
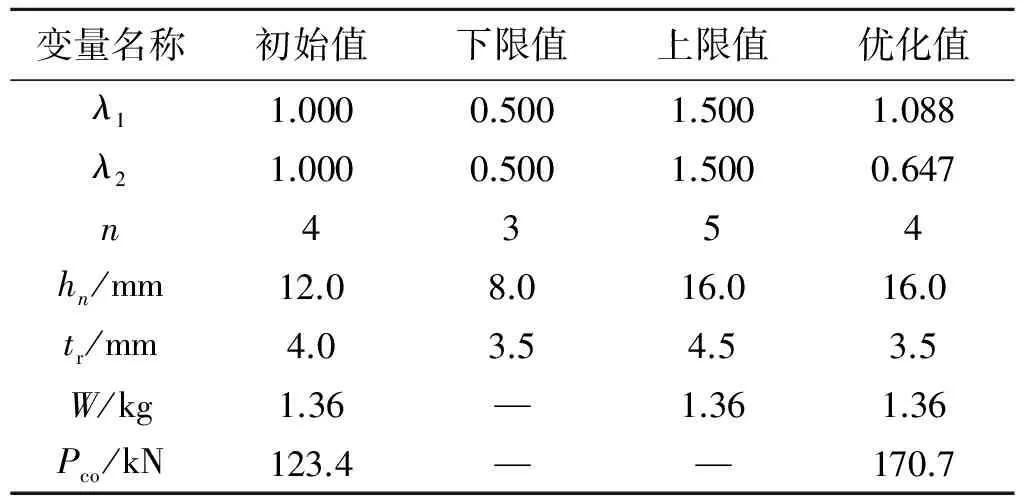
表1 优化1中优化变量的取值范围与优化值

表2 优化2中优化变量的取值范围与优化值
针对以上3个算例,分别基于最优拉丁超立方方法抽取150个样本点后建立代理模型,再抽取另外的12个样本点来校验其误差指标,结果如表4所示,3个算例代理模型的预测精度均满足需求,可用于开展后续的优化设计。如图7所示,历经4次外层更新来不断修正代理模型的精度,优化过程收敛。在保持结构质量不变的情况下,一体化设计优化解的极限承载力(170.7 kN)相较于初始值(123.4 kN)提高了38.3%,且比等尺寸-布局优化解(146.1 kN)提高了16.8%,比等布局、尺寸余弦分布的优化解(144.9 kN)提高了17.8%,这凸显了一体化设计方法在开口补强设计中的巨大优势。需要指出的是,一体化设计优化解(170.7 kN)甚至高于没有开口时完美加筋板的承载力(165.9 kN),进一步表明了新方法的有效性。

表3 优化3中优化变量的取值范围与优化值

表4 3个优化算例中代理模型误差指标
图8~图10分别给出了初始设计、优化1、优化2和优化3的几何构型、位移-载荷曲线和变形云图的对比图。
3个优化算例的优化解与初始设计相比,筋条数目均未发生变化,表明了提高承载力这一目标对筋条数目这一变量并不敏感。优化2为等尺寸-布局优化,其优化解在减小筋条厚度的基础上将筋条高度增加至13.3 mm,有效提高了筋条的抗弯刚度,抑制了局部屈曲变形由开口区向结构整体的扩展,进而提高了结构承载力。相较于优化2,优化1具有更灵活的设计空间,如图8(a)所示,其优化后筋条关于对称中心X轴分布更为紧密,自适应地补强了开口周围的刚度,有利于抑制局部屈曲的过早发生。优化1的筋条高度关于对称中心X轴递减,在开口区域内的筋条高度较低(h0=9.0 mm,h1=11.5 mm),均小于优化2的筋条高度(hr=13.3 mm),表明在开口区域内进行加筋补强的效果并不明显;优化1在近开口区域的筋条高度(h2=13.3 mm)与优化2的筋条高度(hr=13.3 mm)相同,但在位置上更靠近开口区域,有利于抵抗局部屈曲的过早发生,补强优势更明显;优化1在远开口区域的筋条高度(h3=14.7 mm,h4=16.0 mm)均大于优化2的筋条高度,且更靠近开口区域,使筋条具有更大的抗弯刚度,提高了远开口区域筋条抵抗局部屈曲变形扩展的后屈曲承载能力。尽管优化3的优化解中筋条高度变化趋势与优化1的结果较为相似,均表现为向对称中心递减,但需要指出的是,由于优化3仅能改变筋条高度余弦分布函数的幅值,无法自适应地调整布局,因而相较于优化1的设计空间受到限制,未能优化到更优异的结果。综上所述,优化1的优化解相较于初始设计、优化2和优化3的优化解,通过自适应提高近开口区和远开口区筋条的抗弯刚度,对局部屈曲变形发生、后屈曲变形扩展均具有很好的抵抗作用,体现了变截面加筋设计理念在解决开口刚度折减问题上的巨大优势。
4 结论
本文从丰富结构层级的角度提出了一种新型多级加筋板结构形式,并基于代理模型技术建立了尺寸-布局一体化设计框架,通过算例对比得出如下结论:
(1)本文提出的变量函数合理缩减了设计变量的数目,有效表征了变截面多级加筋的尺寸和布局信息。
(2)通过优化算例对比,验证了本文提出的尺寸-布局一体化设计方法的有效性,且相较于传统的等尺寸-布局方法和等布局、尺寸余弦分布方法更易寻找到更优的设计结果。
(3)变截面筋条由于设计变量的灵活性,可自适应地在近开口区域抑制局部屈曲过早发生,并在远开口区域抵抗后屈曲变形的扩展,在开口补强设计中比等截面筋条更具承载优势。
[1] Behavior of compression-loaded quasi-isotropic curved panels with a circular cutout[J]. International Journal of Solids and Structures, 2001, 38(9): 1495-1522.
[2] 展全伟, 范学领, 孙秦. 复合材料孔板在湿热环境下的力学性能研究[J]. 固体火箭技术, 2011, 34(6): 764-767.
[3] Hao P, Wang B, Tian K, et al. Optimization of curvilinearly stiffened panels with single cutout concerning the collapse load[J]. International Journal of Structural Stability and Dynamics, 2015: 1550036-1-1550036-21.
[4] Shi S S, Sun Z, Ren M F, et al. Buckling response of advanced grid stiffened carbon-fiber composite cylindrical shells with reinforced cutouts[J]. Composites Part B: Engineering, 2013, 44(1): 26-33.
[5] Dang T D, Kapania R K, Slemp W C H, et al. Optimization and postbuckling analysis of curvilinear-stiffened panels under multiple-load cases[J]. Journal of Aircraft, 2010, 47(5): 1656-1671.
[6] Hao P, Wang B, Tian K, et al. Efficient optimization of cylindrical stiffened shells with reinforced cutouts by curvilinear stiffeners [J]. AIAA Journal, 2015.
[7] Lakes R. Materials with structural hierarchy[J]. Nature, 1993, 361(6412): 511-515.
[8] Gao H, Ji B, Jäger I L, et al. Materials become insensitive to flaws at nanoscale: lessons from nature[J]. Proceedings of the National Academy of Sciences, 2003, 100(10): 5597-5600.
[9] 王博, 田阔, 郝鹏, 等. 多级加筋板结构承载性能与缺陷敏感度研究[J]. 固体火箭技术, 2014, 37(3): 408-412.
[10] 徐元铭, 李松泽. 整体次加筋壁板屈曲载荷近似计算方法[J]. 北京航空航天大学学报, 2015, 41(3): 369-374.
[11] 隋倩倩, 江舒, 孙方方, 等. 多级三角形格栅夹芯结构力学性能分析[J]. 复合材料学报, 2016,33(3):675-680.
[12] Wang B, Hao P, Li G, et al. Optimum design of hierarchical stiffened shells for low imperfection sensitivity[J]. Acta Mechanica Sinica, 2014, 30(3): 391-402.
[13] Quinn D, Murphy A, Cervi L. Fatigue performance of aircraft panels with novel skin buckling containment features[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2011, 225(7): 791-806.
[14] Houston G, Quinn D, Murphy A, Bron F. Wing panel design with novel skin-buckling containment features[J]. Journal of Aircraft, 2015: 1-11.
[15] Pappas M, Moradi J. Optimal design of ring stiffened cylindrical shells using multiple stiffener sizes[J]. AIAA Journal, 1980, 18(8): 1020-1022.
[16] Khvyiuzov A, Xu Y M. Initial buckling of compressed rectangular panels with variable stiffener sizes[J]. Advanced Materials Research, 2014, 915: 150-164.
[17] Quinn D, Murphy A, Glazebrook C. Aerospace stiffened panel initial sizing with novel skin sub-stiffening features[J]. International Journal of Structural Stability and Dynamics, 2012, 12(5): 1250060.
[18] 冯玉龙, 程家林, 姚卫星. 复合材料加筋板结构的并行空间协同优化设计方法[J]. 南京航空航天大学学报, 2013, 45(3): 360-366.
[19] 荣晓敏, 徐元铭, 吴德财. 进化神经网络在复合材料格栅结构设计中的应用[J]. 固体火箭技术, 2006, 29(4): 305-309.
[20] Wang B, Hao P, Li G, et al. Two-stage size-layout optimization of axially compressed stiffened panels[J]. Structural and Multidisciplinary Optimization, 2014, 50(2): 313-327.
[21] 罗楚养, 熊峻江, 益小苏, 等. 复合材料蒙皮-加筋大开口结构优化设计[J]. 材料工程, 2011(4): 9-13.
[22] Kim J H, Jeon J H, Park J S, et al. Effect of reinforcement on buckling and ultimate strength of perforated plates[J]. International Journal of Mechanical Sciences, 2015, 92: 194-205.
[23] 庄茁. 基于ABAQUS的有限元分析和应用[M]. 北京:清华大学出版社, 2009.
[24] 郝鹏, 王博, 邹威任,等. 基于RBF模型的蒙皮桁条结构减轻孔优化[J]. 固体火箭技术, 2015, 38(5): 717-721.
[25] 陈兵, 谷良贤, 龚春林. 适用于宽马赫数的尾喷管优化设计[J]. 固体火箭技术, 2013, 36(6): 758-762.
[26] 郝鹏. 面向新一代运载火箭的网格加筋柱壳结构优化研究[D]. 大连: 大连理工大学, 2013.
[27] 赵良玉, 杨树兴, 佘浩平. 火箭弹气动学科代理模型构建方法研究[J]. 固体火箭技术, 2007, 30(1): 1-4.
[28] 张柱国, 姚卫星, 刘克龙. 基于进化Kriging模型的金属加筋板结构布局优化方法[J].南京航空航天大学学报, 2008, 40(4): 497-500.
(编辑:薛永利)
Size-layout integrated optimization of variable cross-section stiffened panels
WANG Bo1, TIAN Kuo1,HAO Peng1,ZHENG Yan-bing1, ZHAO Hai-xin1,WANG Jie-bing2
(1.State Key Laboratory of Structural Analysis for Industrial Equipment, Department of Engineering Mechanics,Dalian University of Technology, Dalian 116024, China;2.Science and Technology on Space Physics Laboratory, Beijing 100076, China)
In order to improve the efficiency of cutout reinforcements, a novel variable cross-section stiffened panel was presented in this paper. Due to the hierarchical characteristic of stiffeners, the development of deformations caused by the cutout was restricted effectively, therefore the load-carrying capacity of the stiffened panel increases. Aiming at reducing the number of design variables in the optimization, distribution functions were used to describe both the size and layout variables of stiffeners. Based on the surrogate model, a size-layout integrated optimization framework was established. Finally, the simplicity and effectiveness of the novel optimization framework were validated by comparison with that using uniform size and layout variables and that using uniform layout variables and cosine-type distributed size variables.
hierarchical stiffened panels;cutout reinforcement;load-carrying capacity;integrated optimization
2015-10-09;
2016-01-26。
973项目(2014CB049000);国家自然科学基金(11372062,11402049,91216201);博士后特别资助基金(2015T80246);高等学校学科创新引智计划(B14013);辽宁省高等学校优秀人才支持计划(LJQ2013005)。
王博(1978—),男,教授,主要从事结构与多学科优化、航天先进材料与结构设计和耐撞性优化设计研究。E-mail:wangbo@dlut.edu.cn
郝鹏(1986—),男,博士,主要从事结构可靠性分析与优化研究。E-mail:haopeng@dlut.edu.cn
V414.3
A
1006-2793(2017)02-0208-06
10.7673/j.issn.1006-2793.2017.02.014

