复合固体推进剂双折线脱湿损伤模型参数影响分析

职世君，曹付齐，申志彬，韩 波，李记威

(1.中国空空导弹研究院，洛阳 471000；2.国防科技大学 航天科学与工程学院，长沙 410073)

复合固体推进剂双折线脱湿损伤模型参数影响分析

职世君1，曹付齐1，申志彬2，韩 波1，李记威1

(1.中国空空导弹研究院，洛阳 471000；2.国防科技大学 航天科学与工程学院，长沙 410073)

为分析双折线损伤模型参数对复合固体推进剂细观损伤及宏观非线性力学性能的影响，采用分子动力学方法建立复合固体推进剂颗粒夹杂模型，根据Surface-based cohesive方法，在高氯酸铵(AP)颗粒与基体之间的界面处设置接触损伤。利用有限元方法对具有不同损伤参数的颗粒夹杂模型进行计算，并对比数值仿真结果。结果表明，损伤起始应力对复合固体推进剂抗拉强度、最大延伸率有较大的影响；界面初始刚度在一定程度内的变化，对复合固体推进剂宏观力学性能及细观损伤形貌影响较小；界面失效距离主要影响复合固体推进剂的最大延伸率。

固体推进剂；细观力学；界面损伤；数值模拟

0 引言

复合固体推进剂是一种多相体(基体、增强相、界面相等)复合材料。该类型推进剂具有较良好的力学性能，燃烧稳定。因此，在导弹和宇航火箭发动机中被广泛应用。复合固体推进剂的力学性能和损伤破坏规律受增强相的体积分数及组分材料性质影响较大，但同时也取决于其细观结构特征，这些特征包括增强相的分布规律、形状以及界面相的性质等。早期对复合固体推进剂力学性能的研究，主要基于连续介质力学，不考虑材料的内部细观结构变化，通过大量的固体推进剂力学性能试验确定固体推进剂的非线性本构关系[1-3]。随着对固体推进剂力学性能研究的深入，微裂纹和损伤的影响逐渐引起了许多学者的重视。根据固体推进剂在拉伸载荷下的体积膨胀现象及体积膨胀和材料损伤之间的关系，引进一些数学函数来描述固体推进剂的损伤[4-6]。近年来，随着计算机性能的大幅度提高，计算细观力学得到了迅速发展。Matous等[7-8]利用他们的自主开发软件Rocpack生成了固体推进剂颗粒夹杂模型，并在颗粒与基体之间的界面层设置了cohesive单元模拟了固体颗粒和基体之间损伤的产生及发展。Tan等[9-10]通过数字图象等相关技术获得了高能炸药PBX9501紧凑拉伸试样裂尖周围的应力场及位移场，利用扩展的Mori-Tanaka方法对试验结果做了均匀化处理，从而提取了PBX9501炸药中固体颗粒与基体之间界面损伤的相关参数。随后，又结合试验研究得到颗粒与基体之间的非线性界面损伤模型，对含不同粒径颗粒的细观模型进行了数值计算。国内一些学者也展开了复合固体推进剂的细观力学性能研究。有的学者采用有限元法对复合固体推进剂进行直接数值模拟，对推进剂内部界面脱粘过程进行了有限元分析[11]。有的学者根据数值仿真结果，结合细观力学方法，如：Mori-Tanaka方法或改进的Mori-Tanaka方法，研究了固体推进剂的模量、界面脱粘对固体推进剂力学性能的影响等[12-14]，或采用多步法，将基体与部分颗粒均质化为一种混合物，计算出较复杂的固体推进剂等效模量[15]。

在之前的工作中，已对复合固体推进剂颗粒夹杂模型的几何建模及细观尺度上复合固体推进剂损伤的产生、演化和聚合及其对宏观非线性力学性能的影响进行了研究[16-17]。本文主要在之前的研究基础上，讨论复合固体推进剂双折线脱湿损伤模型参数对其细观损伤形貌及宏观力学性能的影响。

1 物理模型和计算方法

1.1 复合固体推进剂组分及材料属性

根据复合固体推进剂的各组分含量，确定AP颗粒的填充体积分数为65.3%。采用分子动力学方法[17]，建立复合固体推进剂颗粒夹杂模型，如图1所示。复合固体推进剂基体松弛模量如图2所示。

假设AP颗粒为弹性体，取其弹性模量和泊松比分别为E=32 450 MPa，ν=0.143 3[7]。

1.2 Surface-based cohesive方法

Surface-based cohesive方法是基于面与面的接触行为而定义的损伤模型。接触点对的确定采用的是从属表面上的离散点对主控表面进行投影，如图3所示。

从图3可看出，从属表面上的As、Bs和Cs的3个节点分别向主控表面进行投影，取与其距离最短的点为接触点对。在计算时，若对应点不在主控表面的网格节点处，其具体值如位移和接触压力等，则可根据邻近节点的计算结果进行插值计算得到，从而建立了主控表面和从属面的一一对应关系。在接触点对之间引入cohesive损伤模型，便是本文所采用的Surface-based cohesive方法。

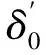
界面的力学响应可描述为

(1)

式中t为界面的名义应力矩阵，包含2个含量，分别代表法向和切向的名义应力；K为界面刚度矩阵。

损伤起始准则取最大名义应力准则，即

(2)

式中tn为法向应力；ts为切向应力；tn0、ts0分别为对应的临界应力；〈〉为麦考利符号。

当界面位移δ达到δ0时，界面开始损伤，界面应力按式(3)、式(4)计算：

(3)

(4)

式中tn和ts分别为无损伤时计算所得到的应力分量；D为损伤因子。

定义损伤因子为

(5)

从图4可看出：

(6)

(7)

故可求得损伤因子为

(8)

式中δ为计算过程中界面张开位移。

2 计算结果与讨论

复合固体推进剂典型的损伤过程一般可分为3个阶段。第1阶段：复合固体推进剂无损伤，颗粒周围真空孔数量很低，或者为零。第2阶段：随着载荷的继续增大，发生脱湿损伤的颗粒逐渐增多，颗粒周围真空孔的数量增加，并在某一点处达到最大值。第3阶段：随着颗粒脱湿损伤的继续演化，前一阶段形成的真空孔不断增大，损伤不断聚合并伴随基体材料的损伤、断裂，最后导致整个复合固体推进剂断裂失效[18]。可见，在复合固体推进剂断裂失效的过程中，颗粒脱湿损伤的影响非常大。

根据图1所示的复合固体推进剂颗粒夹杂模型，对有限元程序进行二次开发，完成颗粒与基体之间接触损伤的自定义，实现复合固体推进剂细观含损伤模型的自动化建模。通过对界面损伤参数反演识别，当取界面损伤参数如表1所示时，采用二维颗粒夹杂模型计算固体推进剂的损伤过程，其表现出的宏观应力-应变曲线与试验结果吻合良好，如图5所示。在损伤的第2阶段，仿真计算的应力-应变曲线没有形成较明显的过渡段，即曲线的第2阶段表现的不明显。这说明采用的界面损伤模型仍需要进一步的完善，但从整体来看，仿真计算的应力-应变曲线与试验曲线较接近，说明该损伤模型可近似表征，并模拟复合固体推进剂的损伤过程。

表1 界面损伤参数

图6为复合固体推进剂颗粒夹杂模型在拉伸载荷下失效时的损伤形貌。从图6可看出，当推进剂在拉伸载荷下失效时，部分颗粒脱湿较严重，颗粒与基体之间形成了较大的空隙。在受载过程中，该区域内的基体材料逐渐被拉成丝状结构，多个颗粒脱湿损伤形成的低应力区域互相影响，从而产生聚合效应，最终导致了固体推进剂失效。虽然文中没有考虑基体材料的开裂及裂纹汇聚过程，无法展现固体推进剂在失效时的断裂，但从图6可看出裂纹产生的位置及开裂时裂纹可能的扩展路径，如图7所示。

为考虑复合固体推进剂颗粒与基体之间界面损伤参数的影响，分别对表2中6组参数进行计算。

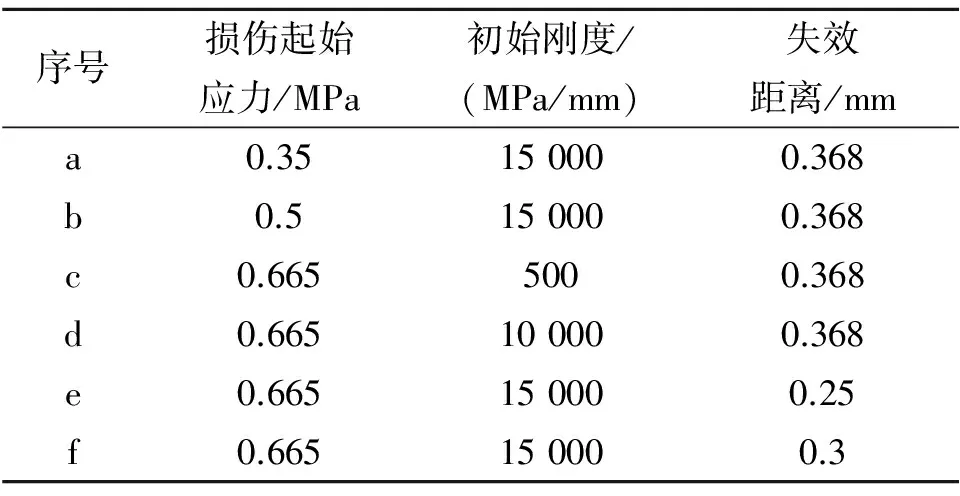
表2 不同的界面损伤参数

2.1 界面损伤起始应力影响分析

表2中，前2组参数考虑的是界面损伤起始应力的影响。图8为界面损伤起始应力分别为0.35、0.5 MPa时颗粒夹杂模型的损伤结果。

对比图6和图8中的结果可看出，颗粒夹杂模型主要的损伤区域没有发生明显的变化，但损伤起始应力的大小对局部区域的损伤演化速率有一定的影响。当损伤起始应力为0.35 MPa时，使得颗粒夹杂模型裂纹可能的扩展路径发生变化，如图9所示。这主要是因为当损伤起始应力为0.35 MPa时，区域A的界面损伤演化速率比区域B快，相应的区域A内的损伤程度较大。随着损伤起始应力的增大，区域B损伤演化速率逐渐增大，当损伤起始应力为0.5 MPa时，区域A和B内的损伤程度基本相当，当损伤起始应力为0.665 MPa时，区域B内的损伤程度比区域A大。因此，形成了图7和图9所示2种可能的裂纹扩展路径。

在全省宣传思想工作会议上，省委书记骆惠宁强调，要以习近平新时代中国特色社会主义思想为指导，立足新方位，担负新使命，奋力推动全省宣传思想工作开创新局面。

图10为复合固体推进剂界面损伤起始应力不同时的应力-应变曲线。从图10可看出，界面损伤起始应力越小，颗粒夹杂模型的损伤起始时间越早，损伤速率越快。因此，相应的抗拉强度和最大延伸率越小。

以上现象可通过双折线损伤模型来解释，如图11所示。从图11可看出，损伤起始应力较小时，对应的界面损伤起始位移也较小，因此容易较早形成损伤，且在损伤产生后，相同的界面张开位移所对应的界面刚度较小，使得在同一阶段，颗粒夹杂模型的整体刚度较低。

2.2 界面初始刚度影响分析

图12(a)、(b)分别是界面刚度为500、10 000 MPa/mm时颗粒夹杂模型的损伤形貌。对比图6可知，界面刚度在500～15 000 MPa/mm范围内的改变，对颗粒夹杂模型最终的损伤形貌并没有太大影响。

图13为界面初始刚度不同时模型的应力-应变曲线。从图13可看出，界面初始刚度为15 000、10 000 MPa/mm时的2条应力-应变曲线较接近，与界面初始刚度为500 MPa/mm的曲线有一定的差异。在起始阶段，该曲线与另2条曲线的差异随拉伸载荷的增大而增大，当拉伸载荷达到一定程度时，该曲线与另2条曲线的差异又随拉伸载荷的增大而减小，到最后阶段，3条曲线逐步趋于重合。

从界面初始刚度不同时的界面损伤模型来解释以上现象，如图14所示。当损伤起始应力一定时，界面初始刚度的不同，使得界面损伤起始位移不同，界面初始刚度越小，界面损伤起始位移越大。

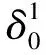
2.3 界面失效距离影响分析

图15(a)、(b)分别是界面失效距离为0.25、0.3 mm时颗粒夹杂模型的损伤形貌。从图15可看出，界面失效距离不同时，模型损伤的区别主要在于形成裂纹时裂纹的最大张开位移不同。界面失效距离越大，颗粒夹杂模型失效时，裂纹的张开位移越大。

图16为颗粒夹杂模型界面失效距离不同时的应力-应变曲线。从图16可看出，3条曲线在起始阶段完全重合，随着拉伸载荷的增大，区别逐渐明显并不断增大，界面失效距离较小的模型首先形成裂纹，界面失效距离大的模型，相应的最大延伸率较大。

图17为界面失效距离不同时的损伤模型示意图。从图17可看出，界面失效距离不同时的区别主要在于刚度衰减阶段。因此，在拉伸的初始阶段，曲线完全重合。随载荷逐渐增大界面开始损伤，损伤程度越大，界面刚度的差异越大。因此，界面失效距离越小，颗粒夹杂模型裂纹产生时的最大张开位移及模型的最大延伸率越小。

3 结论

(1)界面损伤起始应力的大小，在宏观尺度上直接影响复合固体推进剂的抗拉强度和最大延伸率。在细观尺度上，影响局部区域损伤速率，导致裂纹可能的扩展路径产生变化。当模型中形成的裂纹较单一时，界面损伤起始应力越大，复合固体推进剂的抗拉强度和最大延伸率越大。因此，提高颗粒与基体之间的界面强度，可有效改善复合固体推进剂的力学性能。

(2)界面初始刚度在一定范围内的变化，对颗粒夹杂模型的损伤形貌影响较小。在宏观尺度上，对复合固体推进剂的抗拉强度和最大延伸率影响不大。

(3)界面失效距离主要影响复合固体推进剂裂纹形成时的最大张开位移。界面失效距离越大，裂纹形成时的张开位移越大，相应的在宏观尺度上，复合固体推进剂最大延伸率越大。因此，在保证界面损伤起始应力的同时，增大固体推进剂颗粒与基体之间界面的失效距离，可有效提升复合固体推进剂的最大延伸率。

[1] Swanson S R,Christensen L W.A constitutive formulation for high-elongation propellants[J].Journal of Spacecraft,1983,20(6):559-566.

[2] Francis E C,Thompson R E.Nonlinear structural modeling of solid propellants[R].AIAA 84-1290.

[3] Ozupek S,Becker E B.Constitutive modeling of high-elongation solid propellants[J].Journal of Engineering Material and Technology,1992,114(1):111-115.

[4] Gazonas G A.A uniaxial nonlinear viscoelastic constitutive model with damage for M30 gun propellant[J].Mechanics of Materials,1993,15(4):323-335.

[5] Ozupek S,Becker E B.Constitutive equations for solid propellants[J].Journal of Engineering Materials and Technology,1997,119(2):125-132.

[6] Park S W,Schapery R A.A viscoelastic constitutive model for particulate composites with growing damage[J].International Journal of Solids and Structures,1997,34(8):931-947.

[7] Matous K,Inglis H M,Gu X F,et al.Multiscale damage modeling of solid propellants:theory and computational framework[R].AIAA 2005-4347.

[8] Matous K,Geubelle P H.Multiscale modeling of particle debonding in reinforced elastomers subjected to finite deformation[J].International Journal for Numerical Methods in Engineering,2006,65(2):190-223.

[9] Tan H,Liu C,Huang Y,et al.The cohesive law for the particle/matrix interfaces in high explosives[J].Journal of the Mechanics and Physics of Solids,2005,53(8):1892-1917.

[10] Tan H,Huang Y,Liu C,et al.The uniaxial tension of particulate composite materials with nonlinear interface debonding[J].International Journal of Solids and Structures,2007,44(6):1809-1822.

[11] 曲凯,张旭东,李高春.基于内聚力界面脱粘的复合固体推进剂力学性能研究[J].火炸药学报,2008,31(6):77-81.

[12] 李高春,邢耀国,王玉峰.基于细观力学的复合固体推进剂模量预估方法[J].推进技术,2007,28(4):441-444.

[13] 李高春,邢耀国,戢治洪,等.复合固体推进剂细观界面脱粘有限元分析[J].复合材料学报,2011,28(3):229-235.

[14] 刘承武,阳建红,陈飞.改进的Mori-Tanaka法在复合推进剂非线界面脱粘中的应用[J].固体火箭技术,2011,34(1):67-70.

[15] 马昌兵,强洪夫,武文明,等.颗粒增强复合材料有效弹性模量预测的多步法[J].固体力学学报,2010,31(S1):12-16.

[16] Zhi Shi-jun,Sun Bing,Zhang Jian-wei.Multiscale modeling of heterogeneous propellants from particle packing to grain failure using a surface-based cohesive approach[J].Acta Mechanica Sinica,2012,28(3):746-759.

[17] 职世君,孙冰,张建伟.基于表面粘结损伤的复合固体推进剂细观损伤数值模拟[J].推进技术,2013,34(2):273-279.

[18] 阿兰,达文纳斯.固体火箭推进剂技术[M].巴黎:巴黎马森出版社,1989.

(编辑：刘红利)

Parameter analysis of the conduplicate-line dewetting damage model of composite solid propellants

ZHI Shi-jun1，CAO Fu-qi1，SHEN Zhi-bin2，HAN Bo1，LI Ji-wei1

(1.China Airborne Missile Academy，Luoyang 471000，China；2.College of Aerospace Science and Engineering，National University of Defense Technology，Changsha 410073，China)

In order to analyze the influence of parameters of the conduplicate-line damage model on the meso-damage and macro-mechanical properties of composite solid propellants,a particle packing model of the solid propellant was created by molecular dynamics method.The surface-based cohesive approach was adopted to set the interfacial damage between particles and the bind.The packing model with different damage parameters was computed by FEM,and the numerical simulation results were compared.The results show that damage initial stress has a great effect on the tensile strength and maximum elongation of solid propellants.Interfacial initial stiffness changes in a certain extent,which affects the macro-mechanical properties and meso-damage morphology of solid propellants slightly.Interfacial failure distance has a great influence on the maximum elongation of solid propellants.

solid propellant；mesomechanics；interfacial damage；numerical simulation

2015-01-10；

2016-09-30。

国家自然科学基金(U1404106)；“十二五”总装预研项目(51328050101)；国防科技大学科研计划资助项目(JC13-01-03)。

职世君(1983—)，男，博士，研究方向为发动机仿真设计。E-mail： zhishijun@buaa.edu.cn

V512

A

1006-2793(2017)02-0183-06

10.7673/j.issn.1006-2793.2017.02.009