噪声激励下典型复合材料铆接结构的声固耦合分析

廖 涛，李彦斌，吴邵庆，费庆国，董萼良，滕 堪

(1.东南大学 工程力学系，南京 210096；2.江苏省工程力学 重点分析实验室，南京 210096；3.贵州风雷航空军械有限责任公司，安顺 561017)

噪声激励下典型复合材料铆接结构的声固耦合分析

廖 涛1,2，李彦斌1,2，吴邵庆1,2，费庆国1,2，董萼良1,2，滕 堪1,3

(1.东南大学 工程力学系，南京 210096；2.江苏省工程力学 重点分析实验室，南京 210096；3.贵州风雷航空军械有限责任公司，安顺 561017)

针对CVI工艺下复合材料典型铆接板，提出一种适合复杂模型动力学分析的建模方法：采用Bush和RBE2的组合单元模拟铆钉连接，将板间的弱非线性接触力转化为接触刚度，建立该复合材料铆接板的有限元模型。同时，基于有限元-间接边界元法推导了考虑接触力的声固耦合动力学方程，开展了该复合材料铆接板在随机噪声激励下的声固耦合分析，并探讨界面接触对声固耦合系统固有特性和动响应的影响。研究结果表明,界面接触模型比界面刚接模型更为准确；刚接模型会增大复合材料铆接板连接界面的局部刚度，使得结构的固有频率偏高，响应峰值向高频处移动；考虑接触对结构的加速度响应影响较大，对应力响应影响较小。

铆钉连接；界面接触；复合材料；有限元-边界元；声固耦合

0 引言

陶瓷基纤维编织复合材料具有比强度高、比刚度高、密度小、热膨胀系数小以及尺寸稳定性好等特点，被广泛用于航空航天结构(如超声速飞行器)蒙皮、升降舵等结构中[1]。但由于工艺限制，很难直接制备出形状复杂的大型一体化复合材料构件。为了满足结构整体性以及功能性的需要，各部件间需通过大量铆钉、螺栓等连接件进行连接，但连接件的存在会影响结构的整体动力学特性，进而影响飞行器的运行安全。因此，在动力学分析时应考虑连接件的准确动力学建模。同时，飞行器在飞行过程中的随机噪声载荷[2]是结构振动和噪声的主要来源，且飞行器与周围气流的耦合会在结构表面形成高强声压，引起结构的振动。因此，研究复合材料铆接板在噪声激励下的声固耦合问题具有十分重要的应用价值。

在大型复杂结构的有限元建模中[3]，由于自由度较大，常常直接将连接区域直接等效为刚性连接，忽略连接对结构动力特性的影响，进而可能会影响后续动响应分析的准确性。在实际情况中，连接件之间存在着间隙、摩擦等几何非线性因素，对此国内外学者已开展了大量研究。对于螺栓连接结构的建模来说，通常采用各种组合单元对连接件进行简化[4-5]，这些简化模型能极大地提高计算效率，但均未考虑被连接件间的接触问题；Gray P J和McCarth[6]提出了基于螺栓连接组合结构的总体螺栓连接模型，该模型采用壳单元模拟复合材料层合板，螺栓则由一系列梁单元模拟且耦合在刚性接触面上，模型能较好的模拟间隙、层合板间的摩擦、二阶和三阶弯曲等力学性能，但仅限于静力分析，并没有将其运用到动力学分析中来；田红亮等[7]基于赫兹接触与分形理论分析了连接界面的力学模型，运用虚拟材料的方法建立了包括连接界面的整个组合结构的动力学模型，姜东[8]采用参数识别的方法建立了基于薄层单元的连接结构动力学模型，这两种方法将连接界面的接触等效成一种假想的薄层材料，通过赋予该材料一定的属性来模拟接触，所得到的模态分析结果在前几阶与实验吻合较好，但由于这两种方法都是基于统计意义上的平均，所以高阶模态仍与实验结果有不小的误差。

目前，声固耦合的数值分析主要采用有限元-有限元、有限元-边界元[9-10]等方法。有限元-边界元方法中采用边界元模拟声场，与有限元-有限元采用三维实体网格模拟声场相比，具有单元数目少，数据准备简单等优点，被广泛采用。Kruntcheva[11]总结了近50年声场-弹性问题的发展，研究发现声固耦合会显著改变系统的动力学行为，并研究了薄壁结构和声腔模态之间的耦合作用关系；Michael[12]利用有限元-边界元法求出声学频响函数，并将频响函数和随机载荷谱密度联合求解了随机声场；Junge M[13]研究了声固耦合动力学方程的特征值分析问题，并运用快速多级边界元方法来分析船舶等大型结构的流固耦合问题；陈美霞[14-15]和夏齐强[16]等采用有限元-边界元方法分析了壳间不同的连接形式(实肋板、托板、刚接)对双层圆柱壳振动以及声辐射的影响，并将连接件的作用等效为力与弯矩的作用到壳体上，取得了较好结果；姚昊萍[17]通过将板间连接等效成连续分布的弹簧系统来模拟板的不同边界和连接条件，并在此基础上分析了结构之间的耦合以及边界条件的改变对声场的影响。以上研究大多是关于声固耦合对结构固有特性以及声辐射的影响，虽有涉及到壳间连接形式对声辐射的影响，但均未涉及到连接界面间的接触问题。

本文以复合材料铆接板为研究对象，采用组合单元建立基于接触的声固耦合模型，并通过等效线性化的方法将板间的弱非线性接触力转化为接触刚度的形式，进而建立基于有限元-边界元的声固耦合动力学方程。同时，分析该结构在噪声荷载下的声固耦合动力学特性，并探讨界面接触刚度对声固耦合系统固有特性和动响应的影响。

1 考虑接触力的声固耦合动力学方程

1.1 考虑接触力的有限元动力学方程

本文研究的复合材料铆接板所用铆钉通常为CVI工艺在铆钉孔沉积而成，连接的密实性和可靠性较高，因此忽略铆钉与铆钉孔间接触力的作用，仅考虑被连接板间的接触作用。铆钉的预紧力会在被连接板间产生一对接触力，接触力的存在会影响结构的刚度。从非线性平衡出发，结构的节点位移为x时的节点平衡条件为[18]

(1)

式中σ为结构内的应力；B为几何矩阵；N为形状函数矩阵；Ωr为接触面积；f为连接板间的接触力。

两板完全接触阶段，可由接触理论得到接触力的分布函数[19]：

(2)

其中

式中r为被连接板上接触点到铆钉中心点的距离；rA接触半径；D为铆钉直径；L为铆钉杆长度。

接触力产生的结构静位移为x0，结构在动荷载下的位移是在静位移基础上的微幅振动xd(t)，则结构的总位移为

x(t)=x0+xd(t)

(3)

则结构在节点位移为x0+xd时的节点平衡条件为

Ψ(x0+xd)=Ψ(x0)+KT·xd+o(‖xd‖)

(4)

其中，KT为结构在静位移x0状态下的刚度矩阵，包含了接触力引起的初应力的影响，与动态位移xd无关。

设σ0为接触力产生的初应力，σl为微幅振动产生的应力，σ为总应力，则

σ=σ0+σ1

(5)

因为要考虑接触力引起的位移，应变应包含高阶项，即

ε=ε1+εnl

(6)

式中ε1为ε的线性项；εnl为ε的高阶项。

则结构振动应变能为

(7)

根据Hamilton原理并作变分运算，可得到考虑接触力作用下结构的刚度，接触力对结构刚度的影响是在原结构的刚度矩阵上叠加一个应力刚度矩阵，即

KT=K+Knl

(8)

其中

Knl=∭GTSGdV

式中K为不考虑接触力下结构的刚度矩阵；Knl为应力刚度矩阵；B为应变矩阵；D为弹性矩阵；N为形状函数矩阵；s为考虑接触力接触力作用下的应力矩阵。

则由式(1)、式(4)、式(8)可得结构在考虑接触力作用下的动力学方程：

(9)

1.2 基于有限元-边界元的声固耦合动力学方程

将空气视为理想气体，则Helmholtz方程为[9]

▽2p+k2·p=-jρω·q

(10)

式中p为声场任意一点的声压；k为波数，k=ω/c；ω为流体介质运动圆频率；ρ为空气密度；q为空气的单位体积速度。

利用Green核函数公式G(r，ra)改写式(9)可得

▽2G(r，ra)+k2G(r，ra)=-δ(r,ra)

(11)

结构表面的法向振动速度与声压梯度满足

(12)

式中n为结构表面法线方向；vn为结构表面法线振动速度。

利用格林公式，压力辐射域中的Helmholtz微分方程可转为结构边界上Helmholtz积分方程：

(13)

式(13)为直接边界元对应的外场问题边界积分方程，间接边界元方法可从直接边界元法推导出来，将直接边界元的Helmholtz积分方程运用于边界的表面的两侧，然后两方程相减，可得到任意观测点的声压响应[10]，间接边界元以结构边界表面边界元两侧的压力差μ和速度差χ为基本变量。

(14)

其中，μ=p(ra+)-p(ra-)，为压力差矩阵。

对于薄壁空腔结构或者薄壁结构，符合Neuman边界条件，结构表面两侧的法向速度是连续的，因此χ=0，结构表面边界元两侧只有唯一的变量μ。

利用声压的边界元积分和数值近似方法，可得声场波动方程的离散表达式：

Qμ=-jρ0ωAvni

(15)

式中Q为边界元影响矩阵；A为结构表面流体单元面积矩阵。

对于声固耦合结构来说，除结构上直接作用的力或力矩外，还需要考虑由声压差产生的载荷，结构的动力学方程为

(-ω2M+iωC+K+Knl)u=Fs+Fa

(16)

式中Fa为结构与空气耦合面上空气作用在结构上的动压力向量，Fa=-TAμ；T为方向余弦转换阵；μ为结构表面边界元网格两侧压力差；Fs为结构上作用的外激励。

vn=TTv,an=TTa

(17)

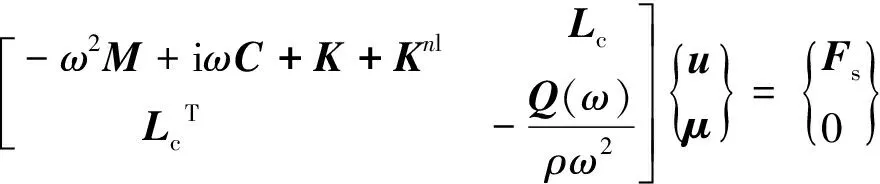
(18)

式中Lc为耦合矩阵，Lc=TA。

结构在噪声激励作用下响应功率谱密度Sx(ω)与激励功率谱密度SF(ω)存在如下关系：

Sx(ω)=H*(ω)SF(ω)HT(ω)

(19)

式中H(ω)为响应相对于激励的频响函数，可由方程式(17)施加单位激励求得；H*(ω)为H(ω)的共轭矩阵。

噪声激励下考虑被连接板间接触作用的结构声固耦合分析流程如图1所示。首先，为了研究界面接触刚度对结构声-固耦合固有特性和动响应的影响，建立以下声固耦合模型：(1)界面接触模型-考虑被连接板间接触刚度的影响；(2)界面刚接模型-将被连接板间的刚度考虑为完全刚性连接。其次，分别进行以上2种模型下声固耦合系统的固有特性分析，并与实验结果对比验证。最后，分别进行随机噪声激励下2种模型的声固耦合动响应分析。

本文的分析计算结果是基于商用有限元软件Patran/Nastran、商用声学软件Virtual.Lab acoustic、Matlab编程以及各软件进行相互调用实现的。

2 算例研究

2.1 典型结构声固耦合模型

最后，教师在使用多媒体设备时也需要合理恰当，不要过度依赖多媒体设备，更恰当的使用多媒体设备可以帮助教师获得更好的教学效果，同时，合理的应用现代网络技术和多媒体技术可以为教师的教学活动提供更多的教学素材，对学生的教学也有一定助力[3]。

本文以陶瓷基纤维编织复合材料铆接板为研究对象，该板由2块几何尺寸为370 mm×280 mm，厚度分别为3 mm和3.5 mm的平板在厚度方向叠合而成，并通过18个φ3.0 mm、18个φ3.5 mm、18个φ8.0 mm的C/SiC铆钉连接，模型示意图如图2所示。C/SiC复合材料材料参数如表1所示。

表 1 C/SiC复合材料材料参数

由于该复合材料板铆钉连接众多，为建立不仅准确而且适合动力学分析的声固耦合模型，提出以下建模方案：

(1) 复合材料上下面板采用壳单元进行建模；

(2) 由于铆钉与构件之间采用的是紧配合的方法组装在一起的，即使用化学气相渗透的方法在铆钉孔与铆钉之间沉积碳化硅，然后对铆钉部位进行加工与修整，制作过程如图3所示。因此其连接强度与可靠性高，因此不考虑铆钉与铆钉孔之间的接触。采用梁单元模拟铆钉，并用RBE2刚性单元连接梁单元与周围的壳单元，用以模拟铆钉与铆钉孔的连接作用。

(3) 当复合材料铆接板承受外荷载作用时，上下面板间不仅通过铆钉传递作用力，而且还会通过板间接触传递作用力。在CVI工艺下，铆钉与两板之间采用紧配合的方法沉积在一起，且铆钉众多，因此可认为两板已达到完全接触。由1.1节可知完全接触下直径3、3.5、8 mm的铆钉的接触半径分别为2.3、2.6、5.13 mm，C/SiC铆钉沉积所得的预紧力按经验取1.4 kN，由式(2)可得3种铆钉周围接触力分布的表达式，进而可求得考虑接触作用力的刚度矩阵Knl，并建立此状态下的结构动力学模型。

(4) 声场部分采用四边形单元在结构外表面建立

边界元模型。基于单元尺寸和波长的关系，所建立的有限元模型可满足每波长内最少6个单元的要求。声学介质为空气，密度1.225 kg/m3，声速 340 m/s。根据以上方案所建立的复合材料铆接板声固耦合模型如图4所示。

2.2 声固耦合系统固有特性分析

为了验证本文所提出的建模方法的准确性，同时也为了分析板间接触对结构声固耦合固有特性的影响。分别对界面接触模型和界面刚接模型进行自由-自由边界条件下的固有模态分析，并与模态实验结果进行对比，以验证模型的准确性，此模态试验采用安正采集与分析系统，通过悬挂法模拟自由-自由边界条件、锤击法获取结构的固有频率以及振型。所得2种模型的固有频率以及实验值如表2所示，前6阶模态振型云图如表3所示。

由表2分析可知，基于界面接触模型和界面刚接模型所得的固有频率与实验结果的最大误差分别为3.8%和14%，说明基于界面接触模型所建立的有限元模型能较好地反映该铆接板的动力学特性，同时，该建模方法所需的单元数目较少，能在保证计算精度的同时极大的提高计算效率。而界面刚接模型则与实验结果误差较大，这是由于直接将界面的节点重合没有考虑到间隙以及摩擦的影响，导致界面“过刚”，从而使得结构的固有频率偏大。由表3可看出，2种模型的模态振型相差不大，说明考虑界面接触对该结构的振型影响很小。

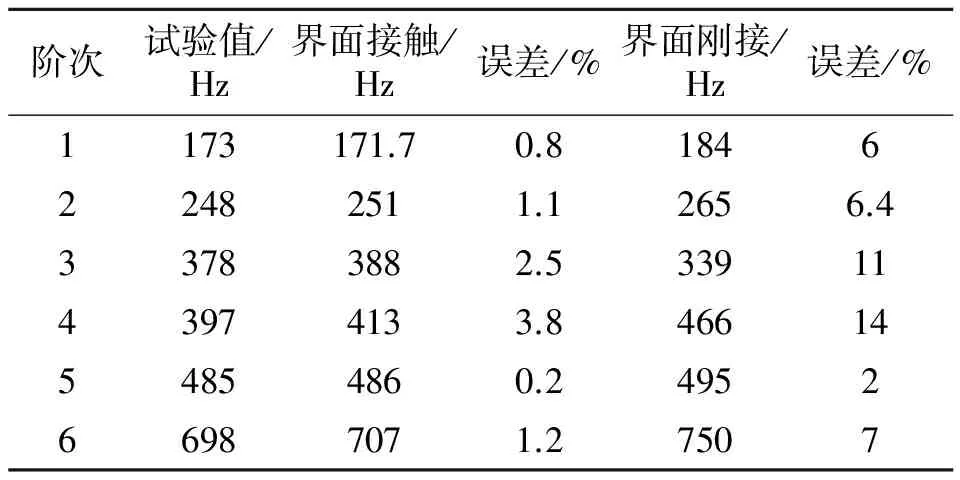
表 2 复合材料铆接板前六阶固有频率

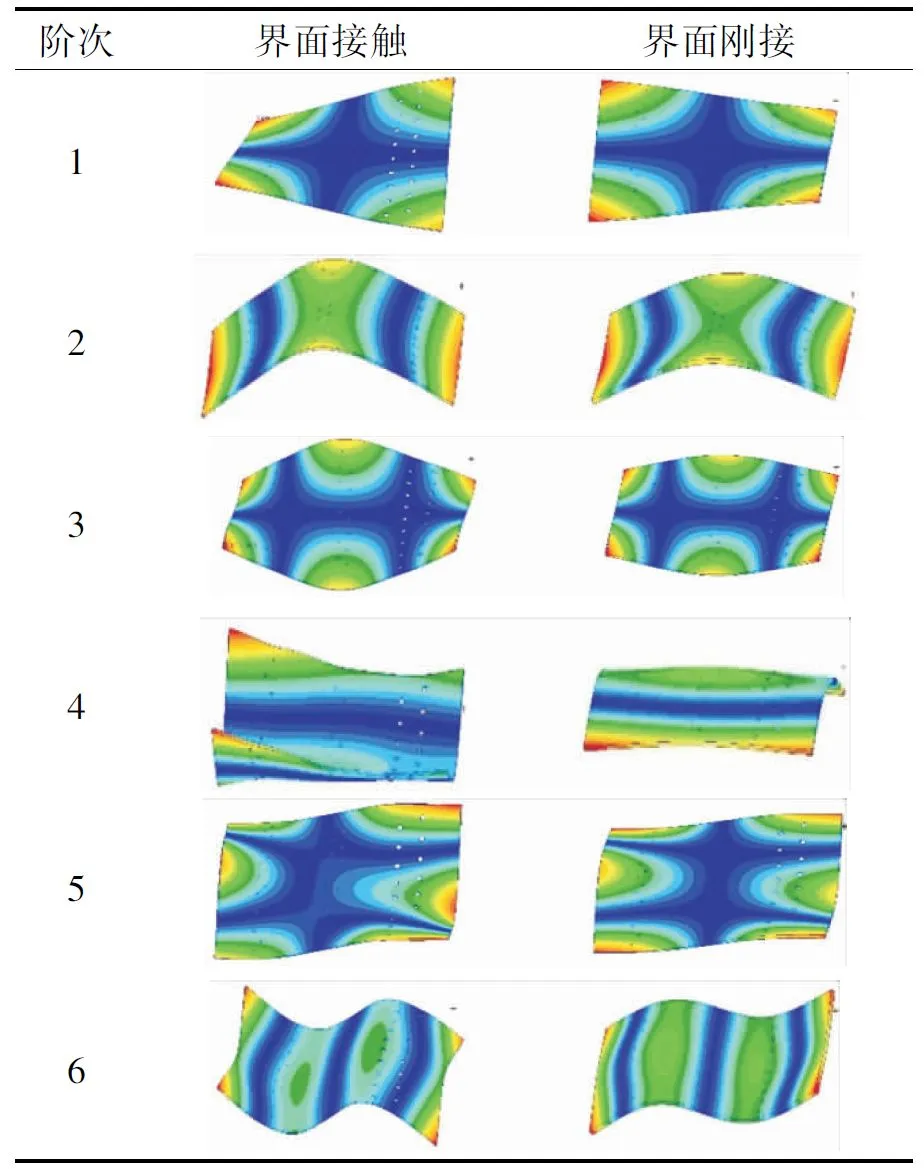
表 3 2种模型下结构的前6阶模态振型

2.3 声固耦合系统动响应分析

为了研究板间接触对复合材料铆接板典型结构声固耦合动响应的影响，进行了界面接触模型和界面刚接模型在随机噪声激励下的动响应分析。

板的边界条件为四边固支，并在板的下表面施加均匀分布的总声压级为146 dB的声激励荷载，声场的激励谱如图5所示。

在板上选取6个典型部位进行分析，其中1、2、3号点位于板边角以及中心处，4、5、6为对应处的铆钉，具体位置如图2所示。图6和图7分别给出了各典型部位的加速度和应力功率谱密度函数曲线，表4给出了各典型部位加速度和应力响应均方根(RMS)。

(a)典型部位3

(b)典型部位5

图 6 典型部位处的加速度功率谱密度函数曲线

Fig.6 PSD of acceleration at typical locations

(a)典型部位1

(b)典型部位2

图 7 典型部位处的应力功率谱密度函数曲线

Fig.7 Stress PSD of each tapical point

由图6、图7可知：

(1)刚接模型会使得响应峰值整体上向高频处移动，这是由于刚接使得复合材料铆接板连接界面局部刚度增大所导致的；

(2)复合材料铆接板在500 Hz左右处出现最大峰值，对应于固支边界条件下结构的一阶固有频率，说明结构的基频模态在结构的动响应分析中起主导作用。

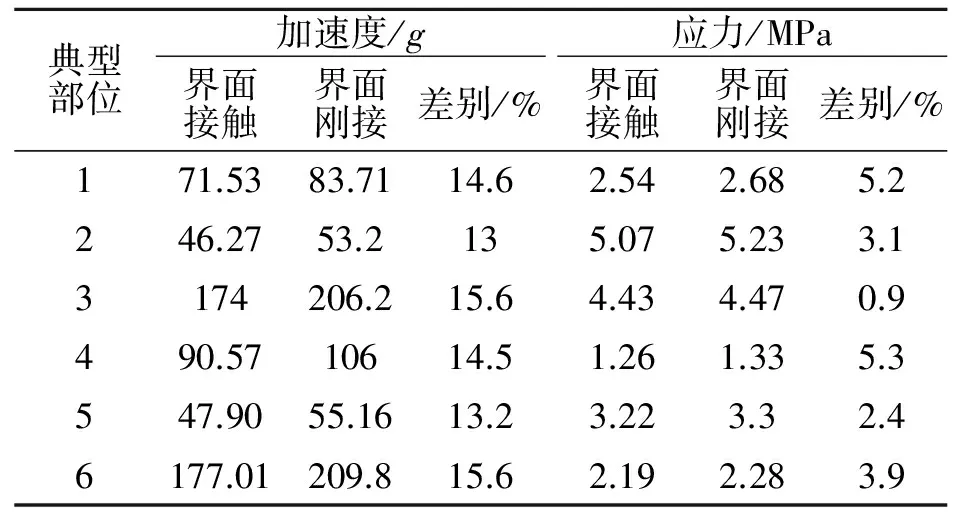
表 4 各典型部位响应均方根

由表4分析可知：

(1)考虑界面接触对结构的加速度响应影响较大，对应力响应影响较小；

(2)刚接模型的加速度RMS值和应力RMS值均大于接触模型的RMS值，由第二节分析可知，这是由于刚接模型使得连接界面局部刚度增大所致；

(3)考虑接触后复合材料铆接板边缘处(1、2号点)应力RMS值改变较大，而几何中心(3号点)处改变较小，且各铆钉处(4、5、6号点)的应力RMS值改变量差异较大，说明接触对钉载的分配有一定影响。

3 结论

(1) 本文以复合材料铆接板为研究对象，提出了一种适合复杂模型动力学分析的简化建模方法：采用Bush和RBE2的组合单元模拟铆钉连接，并将板间的弱非线性接触力转化为接触刚度，建立了该复合材料铆接板的有限元模型。相对于界面刚接模型来说，该模型能极大地提高计算精度。

(2) 界面接触模型模态分析结果与模态试验结果最大误差仅为3.8%，远小于界面刚接模型的最大误差14%，能更准确地反映该结构的动力学特性。

(3) 刚接模型会增大连接界面的局部刚度，使得结构的固有频率增大，响应峰值向高频处移动，且导致结构的加速度RMS值和应力RMS值增大，影响结构的动力学评估的准确性。

(4) 考虑接触对结构的加速度响应影响较大(平均改变量14.4%)，对应力响应影响较小(平均改变量3.5%)，且对复合材料铆接板边缘处(1号点)应力RMS值影响较大，而几何中心处(3号点)影响较小。

[1] Jiang Dong,Li Yan-bin,Fei Qing-guo,et al.Prediction of uncertain elastic parameters of braided composites[J].Composite Structures, 2015,126,123-131.

[2] 马兴瑞,韩增尧,邹元杰,等. 航天器力学环境分析与条件设计研究进展[J].宇航学报, 2012, 33(1): 1-12.

[3] 李彦斌, 姜东, 吴邵庆, 等. 运输载荷下弹体典型连接疲劳寿命评估[J].固体火箭技术, 2013, 36(3): 419-426.

[4] 陈海欢, 刘汉旭, 李泽江. 飞机多钉连接有限元计算与分析[J].航空工程进展. 2012, 3(4):457-462.

[5] Tanlak N,Sonmez F O,Talay E. Detailed and simplified models of bolted joints under impact loading[J].The Journal of Strain Analysis for Engineering Design, 2011, 46(3): 213-225.

[6] Gray P J, McCarthy C T. A global bolted joint model for finite element analysis of load distributions in multi-bolt composite joints[J].Composites Part B: Engineering, 2010, 41(4): 317-325.

[7] 田红亮,刘芙蓉,方子帆,等 .引入各向同性虚拟材料的固定结合部模型[J].振动工程学报, 2013, 26(4):561-573.

[8] 姜东, 吴邵庆, 史勤丰, 等. 基于薄层单元的螺栓连接结构接触面不确定性参数识别[J].工程力学, 2015, 32(4), 220-227.

[9] 李彦斌, 姜东, 吴邵庆, 等. 随机基础激励下承力筒-蒙皮结构的声-固耦合分析[J].宇航学报, 2015, 36(2): 236-242.

[10] 李彦斌, 张鹏, 吴邵庆, 等. 复合材料加筋板计及热效应的声-固耦合分析[J].振动工程学报, 2015, 28(4):531-540.

[11] Allen M J, N Vlahopoulos. Integration of finite element and boundary element methods for calculating the radiated sound from a randomly excited structure[J].Computers and Structures, 2000, 77: 155-169.

[12] Kruntcheva M R.Acoustic-structural resonances of thin-walled structure-gas systems[J].Joumal of Vibration and Acoustics, 2006, 128(6): 722-731.

[13] Junge M, Brunner D,Gaul L.Solution of FE-BE coupled eigenvalue problems for the prediction of the vibro-acoustic behavior of ship-like structures[J].International Journal for Numerical Methods in Engineering,2011,87(7): 664-676.

[14] 陈美霞,骆东平,杨叔子.壳间连接形式对双层壳声辐射性能的影响[J].振动与冲击, 2005, 24(5): 77-82.

[15] Chen M X,Luo D P,Chen Xiaoning, et al. Analytical soultion of radiation sound pressure of double cylindrical shells in fluid medium[J].Applied Mathematics and Mechanics, 2002, 23(4): 463-470.

[16] 夏齐强, 陈志坚. 壳间新连接结构形式下双层圆柱壳声振性能分析[J].噪声与振动控制, 2013(2):54-59.

[17] 姚昊萍, 张建润, 陈南,等. 不同边界条件下的封闭矩形声腔的结构-声耦合分析[J].声学学报,2007, 32(6): 497-502.

[18] Zienkiewicz O C,Taylor R L.The finite element method: its basis and fundamentals, sixth edition[M].Butter-Heinemann; 2005.

[19] Yeh J H, Liou F W. Contact condition modelling for machining fixture setup processes[J].International Journal of Machine Tools and Manufacture, 1999, 39(5): 787-803.

(编辑：薛永利)

Structure-acoustic coupling analysis of a typical composite jointed structure under noise excitation

LIAO Tao1,2, LI Yan-bin1,2, WU Shao-qing1,2, FEI qing-guo1,2, DONG E-liang1,2,TENG Kan1,3

(1.Department of Engineering Mechanics, Southeast University, Nanjing 210096;2.Jiangsu Key Laboratory of Engineering Mechanics, Nanjing 210096;3.Guizhou Fenglei Aviation Ordnance Co., Ltd. Anshun 561017)

Focusing on a typical composite jointed panel in the CVI technology, a finite element model was built in which the riveted joints were simulated by the combined elements of Bush and RBE2 elements, the nonlinear contact forces were transformed to contact stiffness; Utilizing the equivalent linearization method, the equation of motion of the structural-acoustic coupling system was formulated by the FEM-IBEM approach. Structural-acoustic coupling analysis under noise excitation was further conducted and the influence of interfacial contacts on the natural characteristic and dynamic response of this structural-acoustic coupling system was discussed. Results show that the interfacial contact model of the joints is more accurate than the rigid model. The rigid model increases the local interfacial stiffness of the composite jointed panel which will further lead to the increase of the system's nature frequencies. The peaks in frequency domain of the dynamic response of the system with rigid models tend to move towards the higher frequency domain. Interfacial contact has significant influence on structural acceleration but weak effect on stress.

joint; interfacial contacts; composite structure; FEM-BEM; structural acoustic coupling

2015-12-28；

2016-03-01。

国家自然科学基金(11572086 & 11402052)；教育部新世纪优秀人才支持计划(NCET-11-0086)；江苏省自然科学基金(BK20140616)；江苏省普通高校研究生科研创新计划资助项目(CXZZ13_0084)。

廖涛(1992—)，男，硕士，主要从事航天器动力学建模及低频声固耦合研究。E-mail：liaotaonanke@163.com

董萼良，副教授。E-mail：eldong@seu.edu.cn

V259

A

1006-2793(2017)02-0214-07

10.7673/j.issn.1006-2793.2017.02.015