基于收缩理论的高超声速飞行器控制

刘艳雯,胡超芳

(1. 太原工业学院 自动化系，太原 030008;2.天津大学 电气与自动化工程学院，天津 300072)

基于收缩理论的高超声速飞行器控制

刘艳雯1,胡超芳2

(1. 太原工业学院 自动化系，太原 030008;2.天津大学 电气与自动化工程学院，天津 300072)

为了使高超声速飞行器能够跟踪预定指令，针对其严反馈模型提出了基于收缩理论的控制方法。由于高度和速度相对独立，因此分开设计控制器。控制器设计过程中,以基于反步法的收缩理论为核心，对于模型中不确定项利用自适应进行在线识别；引入动态面对虚拟控制输入进行求导，并利用收缩下的奇异摄动分析降阶系统，可以证明降阶前后状态误差间的偏差及滤波误差有界。采用此方法，可证明系统状态半全局收敛，跟踪误差及自适应估计误差有界。

高超声速飞行器；收缩理论；动态面；自适应

0 引言

高超声速飞行器因其速度快、突防能力强、可重复利用等优点，近年来得到各国研究者的关注。常用的控制方法主要有线性控制[1-2]、非线性控制[3-4]、鲁棒控制[5]和自适应控制[6]。其中，由于模型的参数不确定性，在控制过程中利用自适应来在线识别参数具有很大的必要。文献[6-7]采用自适应或者模糊自适应对不确定项进行在线逼近，模糊自适应的优势在于不需要提前预知模型的具体信息。但是不论应用何种自适应方法，对其进行求导都存在很大难度，因此可采用动态面[8]、指令滤波[9]等方法来实现，其中文献[8]为了增强系统鲁棒性，使用扩张状态观测器对不确定状态进行准确估计。近年来，收缩理论[10]成为研究非线性系统轨迹收敛性的一个新方法，它区别于常用的李雅普诺夫方法来进行控制器设计及稳定性分析。其优点在于，即使平衡点位置改变仍然能够判别系统稳定性，另外还能有效拓宽滤波参数的选取范围[11]。

本文在文献[11]的基础上，针对高超声速飞行器模型提出了基于收缩理论的控制方法。其中，利用基于反步法的收缩理论作为整体设计方案；然后利用自适应在线识别不确定参数，并且为了简化控制算法使用了动态面控制。通过收缩理论分析稳定性，可保证闭环系统状态收敛以及系统跟踪误差和自适应估计的有界性。系统仿真结果可证明所提方法的可行性。

1 飞行器纵向模型及其转化

1.1 飞行器模型

本文所采用的高超声速飞行器模型为纵向巡航段模型[12]：

(1)

(2)

(3)

(5)

发动机模型为

(6)

式中V、γ、h、α、q分别为速度、航迹角、高度、攻角和俯仰角速率；m、Iyy、μ、ξ、ωn分别为飞行器质量、俯仰转动惯量、引力常数、发动机阻尼和自然频率；β为油门开度;βc为发动机油门开度设定值；T、L、D、Myy分别为推力、升力、阻力、俯仰力矩，具体表达式可参阅文献[4]。

1.2 模型转化

模型中高度h主要由升降舵偏转角δe控制，速度V由油门开度βc控制，因此模型可划分为速度子系统(1)和高度子系统(2) ～ (5)，并为2个子系统分别设计控制器。

为了使用反步法，首先需要将高度子系统转化成严反馈形式，为此做以下假设：

假设1 式(3) 中的推力项Tsinα相对于升力L非常小, 可忽略。

基于以上假设，可得严反馈形式[13]如下：

(7)

其中，Z1=[V,γ],Z2=[V,γ,α],Z3=[V,α,q],Z41=[V,γ,α],Z42=[V,γ,α,q]。

2 控制器设计

2.1 相关定理引入

定义1(虚位移) 考虑以下非线性系统：

ϑ(υ,t)

(8)

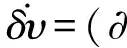
引理1[14](收缩性) 对于系统(8)，ϑ(υ,t)是非线性光滑函数，如果起始于不同初始条件的任意2条轨迹是相互指数收敛的，那么系统是收缩的。收缩性的一个充分条件是：如果存在某种矩阵测度μ，对于任意υ,t>0，都有λ>0使得μ(∂ϑ(υ,t)/∂υ)≤-λ成立，那么系统是收缩的，λ称作收缩率。

本文中判定系统收缩性的矩阵测度为

式中λmax(·)为矩阵最大特征值。

如果系统采用的连接方式为分层连接，则系统所具有的虚拟动态如下：

(9)

如果子矩阵F11和F22是一致负定的，且F12有界，那么整个系统的任意一条轨迹都是指数收敛的。

对于标准奇异摄动系统：

(10)

定义2 (部分收缩) 对任意z及时间t，如果虚拟系统：

(11)

是收缩的，就称系统(10)对x是部分收缩的。

同样，对任意x和ε，如果虚拟系统：

(12)

是收缩的，则称系统(10)对z是部分收缩的。

引理2[11]定义全局可微函数γ(x):=γ(x,0)，如果系统(10)满足下述条件：

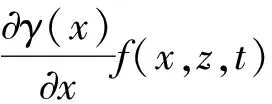
(2)f(x,z,t)在z域中关于常数α是Lipschitz连续的，对x也是部分收缩的，λx是(11)的收缩率。

上述条件若成立，且γ(x)在x域中关于常数αγ也是Lipschitz连续的，记xγ是如下降阶系统的一个解：

(13)

那么系统(10)的任意轨迹满足：

‖x(t)-xγ(t)‖ ≤χx‖x(0)-xγ(0)‖e-λxt+

ε(C1(e-λxt-e-(λz/ε)t)+

C2(1-e-λxt)).∀t≥0

(14)

‖z(t)-γ(xγ(t))‖ ≤ ‖z(0)-γ(x(0))‖χze-(λz/ε)t+

(d+K)χz/γzε+

αγχx‖x(0)-xγ(0)‖e-λxt+

αγε(C1(e-λxt-e-(λz/ε)t)+

C2(1-e-λxt)).∀t≥0

(15)

其中

式中χx、χz分别为Θx和Θz条件数的上界。

2.2 高度子系统控制器设计

针对转化模型(7)，设计控制器使得输出状态h、V能够跟踪指令hd、Vd。设计过程中，高度和速度两子系统相对独立，可分开设计控制器。

由式(7)可知，输出状态h是由δe控制的四阶系统，并且在高度子系统设计中认为速度V是常数。从式(2)可知，高度和航迹角状态是一一对应的，故可转化得到航迹角指令γd：

(16)

其中，ki,i=h,1,2,3,4是正的设计参数。

第一步：定义误差面z1=γ-γd，求导后可得

(17)

其中，g1仅与V相关，因此结合其表达式可认为g1为正常数；fi(·)为未知的非线性函数，因此利用自适应进行在线逼近：

(18)

(19)

(20)

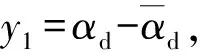
(21)

第二步：对误差面z2=α-αd求导后可得

(22)

(23)

(24)

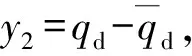
(25)

第三步：对误差面z3=q-qd求导后可得

(26)

式中 g3为正常数。

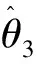
(27)

将式(27)带入后可得如下形式：

(28)

2.3 速度子系统控制器设计

速度子系统仅为一阶系统，因此利用收缩理论进行控制相对简单。定义速度跟踪误差z4=V-Vd,求导后可得

(29)

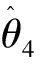
(30)

将式(30)带入后可得如下形式：

(31)

3 稳定性证明

对于高度子系统，令fi(Zi)满足：

式中li为正常数。

通过调节参数使得

负定成立，即使得ηi<1/(ki+li),i=1,2，因此式(20)、式(24)对yi是部分收缩的。

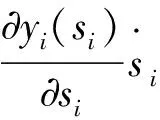
(32)

i=1,2的一个解，那么由引理2可得

‖zi(t)-ziγ(t)‖≤‖zi(0)-ziγ(0)‖e-kit+

e-kit∏i+τi(Ci1Ei1+Ci2Ei2)

(33)

‖yi(t)‖≤‖yi(0)‖e-(Li/τi)t+Miτi

(34)

由于最后一阶子系统不包含滤波，因此无需采用奇异摄动分析，故第n阶子系统的原系统轨迹与降阶系统轨迹是同一条轨迹，即z3(t)≡z3γ(t)。

而对于速度子系统，由于其是一阶的，类似于以上分析很容易证明z4(t)≡z4γ(t)。

对于每一步降阶子系统进行整理，可得变换后的降阶系统综合形式：

ϖZγ

(35)

其中

ϖ

可看出降阶后系统呈分层结构，选取适当的参数ki,i=1,2,3使μ(ϖ)≤-λ1,(λ1>0)成立。结合引理1，可知降阶后的系统状态是收缩的，系统轨迹渐近收敛到期望轨迹，即降阶系统的跟踪误差渐近收敛到0。

综上，则式(36)成立：

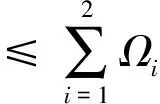
(36)

此外，高度子系统第一阶、最后一阶动态和速度动态的自适应律属于典型的收缩自适应控制，参考以下引理。

引理3如果系统满足以下虚拟动态：

自适应可构成以下形式：

(37)

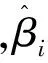
综上可得，原系统状态是半全局收敛的，且收敛域为以期望轨迹为中心的很小范围内。应用以上方法，可拓宽滤波参数范围，同时可保证滤波器误差以及自适应估计误差的半全局有界性，进而保证了原闭环系统跟踪误差的有界性。

4 仿真分析

对高超声速飞行器模型进行数值仿真，状态初始值设为V=4.59 km/s;α=0.031 5;γ=0;q=0;h=33.53 km。高度和速度指令分别为0.61 km和0.03 km/s的阶跃信号。主要控制参数选取为:kh=1,k1=10,k2=6,k3=4,k4=0.5,η1=0.02,η2=0.02。按照本文所提方法设计控制器，仿真结果如图1～图4。

图3、图4表明了输入信号油门开度和升降舵偏角的变化情况。从图中可知，油门开度和升降舵偏角处在合理范围内变化，控制结果基本可以保证控制要求。

本方法区别于李雅普诺夫稳定性分析方法，除了控制器设计更加简单、计算速度更快以外，控制效果也有所改善。图5、图6为本文所提方法与经典李雅普诺夫方法(复现文献[4]仿真结果)下速度和高度的跟踪对比图，从图中可知，基于扩张理论的控制方法控制精度更高。

5 结论

(1)本文所提控制方法利用基于收缩理论的自适应方法在线估计系统中的不确定参数，结合动态面方法在减少计算量的同时大大提高了运算速度，经仿真验证该方法控制精度可达到控制要求。

(2)以收缩为核心的控制理论与方法，将传统稳定性分析转换成对矩阵的运算，在保证系统的稳定性的同时使得控制器设计更加简单，为系统分析与设计提供了思路。

[1] 于璐,杨剑影.高超声速飞行器高阶纵向模型的控制器设计和性能分析仿真[J].战术导弹技术，2010(3):92-95.

[2] Gao Huijun,Si Yulin.Modeling and control of an air-breathing hypersonic vehicle[C]//Proceedings of the 7th Asian Control Conference.Hong Kong,China,August27-29,2009:304-307.

[3] 刘燕斌,陆宇平.基于反步法的高超音速飞行器纵向动态逆控制[J].控制与决策，2007,22(3):313-317.

[4] 高道祥，孙增圻，罗熊.基于Backstepping的高超声速飞行器模糊自适应控制[J].控制理论与应用,2008,25(5):805-810.

[5] 陈雪芹，耿云海，张世杰.基于H2/H∞的集成故障诊断与容错控制研究[J].宇航学报，2007,28(4):890-897.

[6] Lian B H,Bang H,Hurtado J E.Adaptive backstepping control based autopilot design for reentry vehicle[C]// AIAA Guidance,Navigation,and Control Conf and Exhibit,2004.

[7] 李静,左斌,段洣毅,等.输入受限的吸气式高超声速飞行器自适应Terminal滑模控制[J].航空学报,2012,02:220-233.

[8] 刘晓东,黄万伟,禹春梅.含扩张状态观测器的高超声速飞行器动态面姿态控制[J].宇航学报,2015,36(8):916-922.

[9] 黄喜元,王青,董朝阳.基于Backstepping的高超声速飞行器鲁棒自适应控制[J].系统工程与电子技术,2011(6):1321-1326.

[10] Pham Q C,Tabareau N,Slotine J J E.A contraction theory approach to stochastic incremental stability[J].IEEE Transactions on Automatic Control,2009,54(4):816-820.

[11] 胡超芳,张志鹏.基于收缩理论的一类非线性系统自适应动态面控制[J].控制与决策,2016,31(5):769-775.

[12] Xu H J,Mirmirani M.Adaptive sliding mode control design for a hypersonic flight Vehicle[J].Journal of Guidance Control,and Dynamic,2004,27(5),829-838.

[13] 胡超芳,刘艳雯.基于动态面的高超声速飞行器模糊自适应非线性控制[J].控制与决策,2013,29(12):1849-1854.

[14] Del Vecchio D,Slotine J J E.A contraction theory approach to singularly perturbed systems[J].IEEE Transactions on Automatic Control,2013,53(3):752-757.

(编辑：吕耀辉)

Contraction theory-based control for hypersonic vehicle

LIU Yan-wen1,HU Chao-fang2

(1.School of Automation,Taiyuan Institute of Technology,Taiyuan 030008,China;2.School of Electrical Engineering and Automation,Tianjin University,Tianjin 300072,China)

In order to track a predetermined instruction for the hypersonic vehicle,a control method was proposed for its strict feedback model based on the theory of contraction.Due to the relative independence of attitude and speed subsystems,controllers was designed separately.During the design process,on the basis of the contraction theory,adaptive control was adopted to identify the model uncertainty online.Moreover,the contraction-based singular perturbation analysis is used to reduce the subsystem dynamics.By analyzing the contraction-based robustness of the hierarchical interconnection of the subsystems,it can be proved that the differences of the state errors between the original and the reduced subsystems and the differences of the filters are explicitly bounded.With this method introduced,the total system state of the hypersonic vehicle can converge to a ball centered about the desired trajectory semi-globally.

hypersonic vehicle；contraction theory；dynamic surface control；adaptive control

2016-07-27；

2016-10-14。

太原工业学院青年科学基金(2015LQ08);天津市自然科学基金 (12JCZDJC30300)。

刘艳雯(1987—)，女，硕士，从事飞行器的鲁棒控制研究。E-mail：azhenwen@163.com

V448

A

1006-2793(2017)02-0264-05

10.7673/j.issn.1006-2793.2017.02.023