由一道最值问题谈分式型柯西不等式的应用

■郑州外国语学校 杨春波 邱培云

1.引例

在必修五第三章《基本不等式》一节的日常练习中有这样一道题目:已知正数x,y满足x+y=1,求的最小值。

此题有如下两种常见解法:

解法1将所求最小值的式子乘以常数1(即x+y),解法2将所求最小值式子分子中的常数1用x+y进行代换,这都属于“1”的巧妙运用,目的是构造出乘积为定值的式子,为基本不等式的运用创造条件。不可否认,以上解法具有一定的技巧性,同学们首次碰到这类问题时很难独立想到。需要指出的是,这类分式最值问题其实可用分式型柯西不等式求解。下面为同学们介绍分式型柯西不等式的具体内容,并举例说明它在解题中的应用。

2.分式型柯西不等式

在选修4-5《不等式选讲》中,有二维形式的柯西不等式:设x1,x2,y1,y2∈R,则:

≥(x1y1+x2y2)2,当且仅当x1y2=x2y1时,等号成立(证明过程略)。

二维的分式型柯西不等式只是上述不等式的变形:设x1,x2∈R,y1,y2＞0,则:

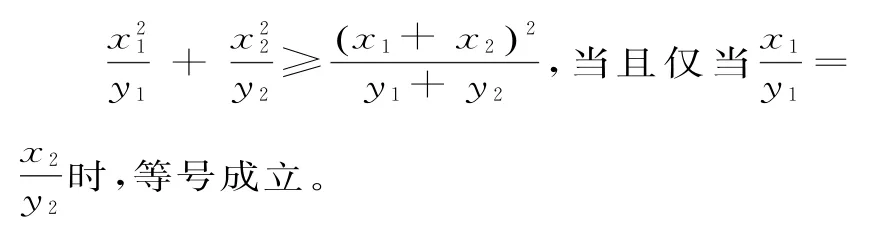
证明：由柯西不等式得:

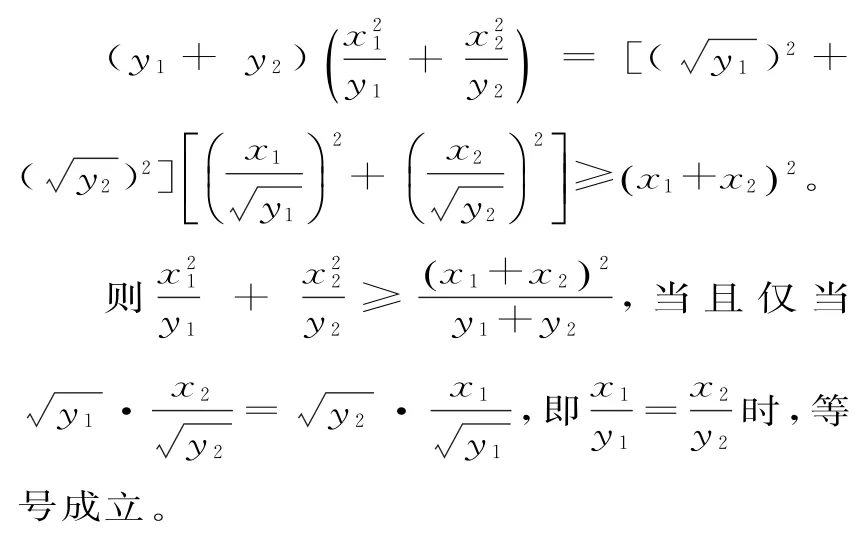
其实,我们也可直接用分析法给出证明:已知y,y＞0,要证≥12即证(y1+y2)+(y1+y2)≥(x1+x2)2y1y2。展开整理得+≥2x1x2y1y2,亦即(x1y2-x2y1)2≥0,显然成立,当且仅当xy=xy,即时,等号1221成立。

多次运用二维形式的分式型柯西不等式,便可将其推广到三维形式以及n维形式。

三维分式型柯西不等式:设x1,x2,x3∈R,y1,y2,y3＞0,则:

证明：由二维分式型柯西不等式知:

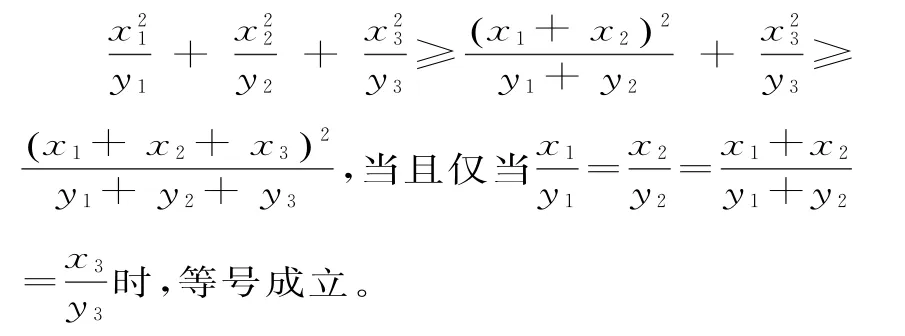
n维分式型柯西不等式:设x1,x2,…,xn∈R,y1,y2,…,yn＞0,则:

3.分式型柯西不等式应用举例

分式型柯西不等式在处理分式最值问题时简单快捷,十分有效,因为它既不需要像基本不等式那样巧用常数,也不需要像柯西不等式那样配凑数组。比如用分式型柯西不等式解决文章开头的引例:(1 +)2=3+2,当且仅当,即y=x=2-时取等号,故所求最小值为3+2。

3.1求解最值问题

求函数y=在)上的最小值。

若正数x,y满足x+3y=5xy,求3x+4y的最小值。

已知正数x,y满足x+y=10,求x+y的最小值和最大值。

若a＞b＞c,则有最小值,还是有最大值?并求出对应值。

3.2证明不等式

设a,b,c∈R,且a+b+c=1,求证:a2+b2+c2。

证明：a2+b2+c2=。

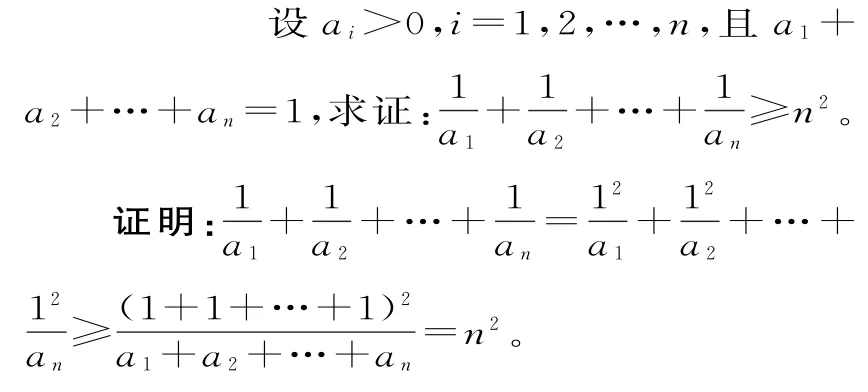
(2009年南京大学自主招生试题)P为△ABC内一点,它到三边BC,CA,AB的距离分别为d1,d2,d3,S为△ABC的面积,求证:(这里a,b,c分别表示BC,CA,AB的长度)

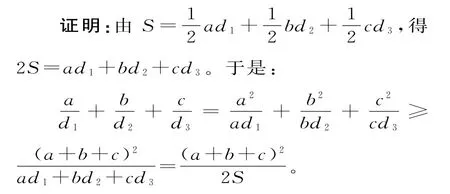
3.3综合问题

设a＞0,b＞0,且不等式≥0恒成立,求实数k的取值范围。

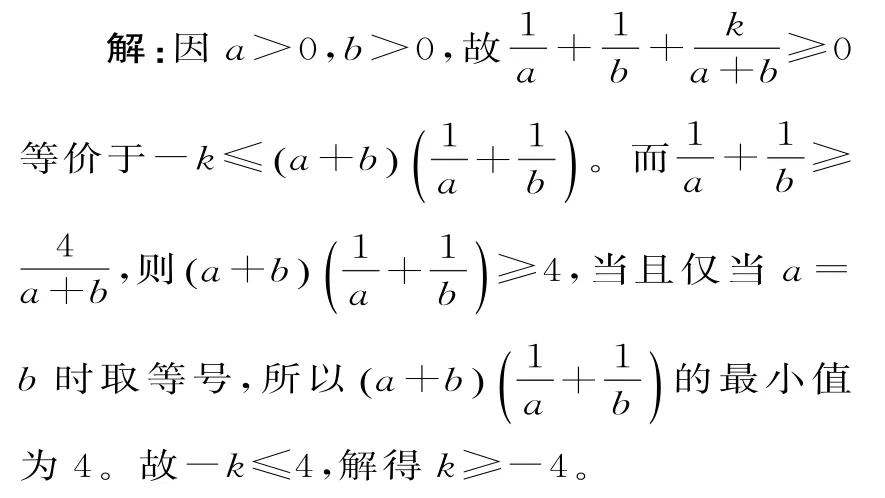
已知不等式(x +y)≥9对任意正实数x,y恒成立,求正数a的最小值。

解：(x+y)≥(x+y)(1+)2,当且仅当等号成立,故(x+y)·的最小值为

若直线2ax-by+2=0(a＞0,b＞0)被圆x2+y2+2x-4y+1=0截得的弦长为4,求的最小值。

解：x2+y2+2x-4y+1=0,即(x+1)2+(y-2)2=4,表示以 (- 1,2)为圆心,以2为半径的圆。又直线2ax-by+2=0被圆截得的弦长为4(直径长),故直线通过圆心,a+b=1。3+2,当且仅当b=a=2-时取等号,故最小值为3+2。(1+)2,因此。(1+a)2≥9,a≥4,即正数a的最小值为4。

已知正项等比数列{an}满足a7=a6+2a5,若存在两项am,ak,使得=4a,求的最小值。1

解：设公比为q,则a7=a6+2a5,整理得q2=q+2,得q=2或-1(舍去)。=4a1,即=4a1,得m+k=6。仿前可求的最小值为。

已知=23,∠BAC=30°。M 是△ABC内一点,不含边界,设△MBC,△MCA,△MAB的面积分别为x,y,z,则称(x,y,z)为点M的面积坐标。记f(x,y,z)=,求使f(x,y,z)取得最小值时的点M的面积坐标。

解：△ABC的面积S=AB·AC·sin∠BAC=·tan∠BAC=1,则x+y+z=1。所以f(x,y,z)==36,当且仅当,即x=,z=时取等号,则f(x,y,z)的最小值为36,此时点M的面积坐标为。