椭圆测试卷(A卷)参考答案
一、选择题
1.D 2.A 3.C 4.D 5.C 6.D 7.C 8.D 9.B 10.C 11.B 12.D 13.C 14.A 15.D
16.C 提示:当∠PF1F2为直角时,根据椭圆的对称性知,这样的点P有2个。同理,当∠PF2F1为直角时,这样的点P有2个;当P点为椭圆的短轴端点时,∠F1PF2最大,且为直角,此时这样的点P有2个。故符合要求的点P有6个。
17.C

19.D 提示:由椭圆的方程可知a=2。由椭圆的定义可知,|AF2|+|BF2|+|AB|=4a=8,所以|AB|=8-(|AF2|+|BF2|)≥3。由椭圆的性质可知,过椭圆焦点的弦中,通径最短,则3,所以b2=3,即b=。
20.D
21.A 提示:依题意知,点M在以F(3,0)为圆心,1为半径的圆上,PM为圆的切线,当最小时,切线长最小。
22.D 23.A 24.C 25.B 26.A 27.D 28.B
二、填空题
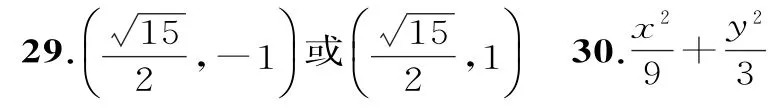
33.7
34=1 提示:设|BF|=x,则2=3x,x>0,由椭圆的定义得|AF1|=2a-|AF2|=23-3x,|BF1|=2a-|BF2|=23-x。在△AF1B中,由余弦定理得|BF1|2=|AF1|2+|AB|2-2|AF1|·|AB|cos∠F1AB,即(2-x)2=(2-3x)2+(4x)2-2·(2-3x)·4x·cos60°,解得x=。在△AFF中,由余弦定理得|F1F2|2=|AF1|2+|AF2|2-2|AF1|·|AF2|cos∠F1AB,即 4c2=+-2· ·cos60°,解得c=1。故b2=a2-c2=2,所以椭圆C的标准方程为=1。
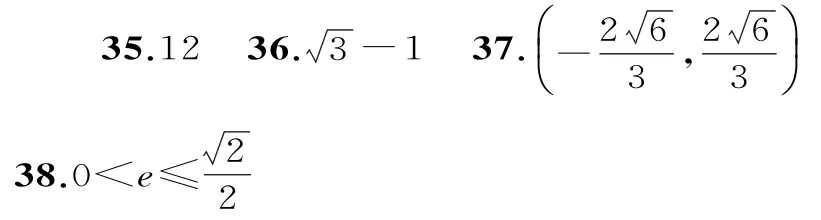
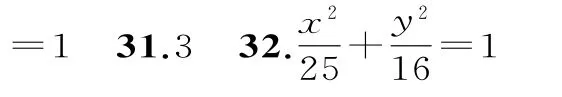
三、解答题
39.(1)c的离心率为。(2)a=7,b=27。

(2)因为点B与点A关于x轴对称,所以B(m,-n)。设N(x,0),则x=。NN“存在点Q(0,yQ)使得∠OQM=∠ONQ”等价于“存在点Q(0,y)使得”,Q即yQ满足=|xM|·|xN|。因为xM==1,所以===2,y=或y=QQ-。故在y轴上存在点Q,使得∠OQM=∠ONQ,点Q的坐标为(0)或(0,-)。

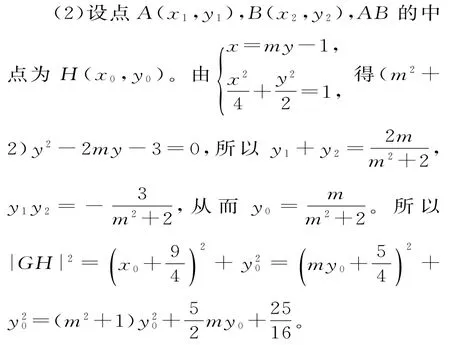

42.(1)椭圆的离心率e=。(2)由(1)知a2=2c2,b2=c2。故椭圆方程为=1。设P(x0,y0)。由F1(-c,0),B(0,c),得=(x0+c,y0)=(c,c)。由已知,有=0,即(x0+c)c+y0c=0。又c≠0,故有x0+y0+c=0。①又因为点P在椭圆上,故=1。②由①和②可得+4cx0=0,而点P不是椭圆的顶点,故x=-,代入①得y=,即00点P的坐标为。设圆的圆心为T(x,y),则x=c,进而圆的111半径r==。设直线l的斜率为k,依题意,直线l的方程为y=kx。由l与圆相切,可得,整理得k2-8k+1=0,k=4±。所以直线l的斜率为4+或4-。

(2)设M(x1,y1),N(x2,y2),A(x3,y3),B(x4,y4),由(1)得:

44.(1)E的方程为=1。

45.(1)点E的轨迹方程为=1(y≠0)。
(2)当l与x轴不垂直时,设l的方程为y=k(x-1)(k≠0),M(x1,y1),N(x2,y2)。
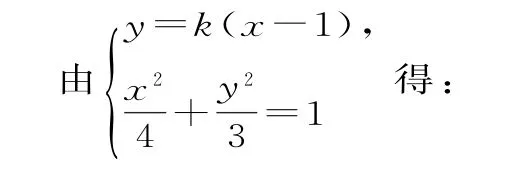
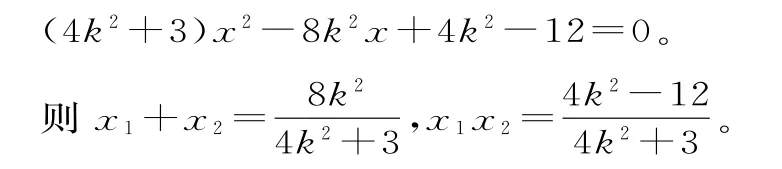
所以|MN|=1+k2|x1-x2|=。过点B(1,0)且与l垂直的直线m:y=(x-1),A到m的距离为,所以|PQ|==。故四边形MPNQ的面积S=MN||PQ|=12。可得当l与x轴不垂直时,四边形MPNQ面积的取值范围为(12,83)。当l与x轴垂直时,其方程为x=1,|MN|=3,|PQ|=8,四边形MPNQ的面积为12。
综上,四边形MPNQ面积的取值范围为[12,8)。
46.(1)椭圆C的标准方程为+y2=1。
(2)证明:设点A,B,M的坐标分别为A(x1,y1),B(x2,y2),M(0,y0)。易知F点的坐标为(2,0)。显然直线l存在斜率,设直线l的斜率为k,则直线l的方程是y=k(x-2)。将直线l的方程代入到椭圆C的方程中,消去y并整理得(1+5k2)x2-20k2x+20k2-5=0,故x1+x2=,x1x2=。