常用逻辑用语单元检测题（B卷）参考答案

一、选择题

1.A 2.D 3.B 4.B 5.A 6.C 7.C 8.B 9.B

10.A 提示:当a=-3时,圆(x-3)2+y2=4的圆心为(3,0),半径r1=2,与圆x2+y2=1相外切;当两圆相内切时,a=±1,故选A。

11.D 12.D 13.B

14.B 提示:命题p为假,因为当x＜0时,2x＞3x。命题q为真,因为f(x)=x3+x2-1在(0,+∞)内单调递增,且f(0)=-1＜0,f(1)=1＞0,所以在(0,1)内函数f(x)必存在零点。则﹁p∧q为真命题,故选B。

15.A

16.A 提示:函数f(x)=x2-4ax+3的对称轴为x=2a,则在 [2 a ,+∞)上函数递增;若函数f(x)=x2-4ax+3在区间[2,+∞)上为增函数,则2a≤2,得a≤1。

所以“a=1”是“函数f(x)=x2-4ax+3在区间2,+∞[)上为增函数”的充分不必要条件。

17.D 18.B 19.B

20.A 提示:由题意得,“lgy为lgx,lgz的等差中项”,则2lgy=lgx+lgz⇒y2=xz,故“y是x,z的等比中项”;而当y2=xz时,如x=z=1,y=-1时,“lgy为lgx,lgz的等差中项”不成立,所以“lgy为lgx,lgz的等差中项”是“y是x,z的等比中项”的充分不必要条件。

21.D 提示:当A、B均为锐角时,由函数的单调性及不等式的性质知都成立;当B为锐角,A为钝角或直角时,且A、B为三角形的内角,所以≤A＜π,0＜B＜,A+B＜π,即,B＜π-A＜,故tan＞tan,sinB＜sin(π-A)=sinA,cosB＞cos(π-A)=-cosA≥0,所以cos2A＜cos2B。

22.B

23.C 提示:A.可以推得为既不充分也不必要条件;B.可以推得=为必要不充分条件;C.为充分不必要条件;D.同B。所以选C。

42.(2) 提示:(1)中命题的否定为∃x0＞0-x0＞0;(2)中A＞B得a＞b由正弦定理得,故sinA＞sinB;(3)中由“an,an+1,an+2成等比数列”可得=anan+2”成立,反之不成立,如an+1=an=an+2=0时;(4)中只有当lgx＞0时函数f(x)的最小值为2,所以真命题为(2)。

43.a≤-2或a=1

44.[1,+∞) 提示:由题设可得p,q都为假命题,命题p:∃x0∈R,mex0+1≤0,则﹁p:∀x∈R,mex+1＞0,恒成立是真命题,即m＞-＜0⇒m≥0;命题q:∀x∈R,

24.D 25.C 26.D

27.D ﹁q∧r是真命题意味着﹁q为真,q为假(乙没得第二名)且r为真(丙得第三名);p∨q是真命题,由于q为假,只能p为真(甲得第一名),这与p∧q是假命题相吻合;由于还有其他三名队员参赛,只能肯定其他队员得第二名,乙没得第二名,故选D。

28.B 29.C 30.C

二、填空题

31.真 32.1 33.∀x∈R,2x2-3x+9≥0 34.充要

35.若ac≤0,则方程ax2-bx+c=0(a≠0)的两根不全大于0

36.3≤m＜8 37.充分不必要 38.②④39.-3≤a≤0 40.[3,+∞) 41.[-1,6]x2-2mx+1＞0是假命题,故﹁q:∃x0∈R-2mx0+1≤0是真命题,故4m2-4≥0,m≥1或m≤-1,则m≥1,m的取值范围为[1,+∞)。

45.(-∞,2]

46.(0,2) 提示:﹁p是﹁q的充分不必要条件,等价于p是q的必要不充分条件。由题意得f(x)为偶函数,且在(0,+∞)单调递增,在(-∞,0)单调递减,由p:f(x+1)＞f(2x-1)得f(|x+1|)＞f(|2x-1|),即|x+1|＞|2x-1|,解得0＜x＜2。

由q:(x-1)(x-m)≤0,知m的取值范围是(0,2)。

47.a≤-2或a=1 提示:对∀x∈[1,2],x2-a≥0,即a≤(x2)min=1,即命题p:a≤1;∃x0∈R,x2+2ax+2-a=0,即x2+2ax+2-a=0有实根,则4a2-4(2-a)≥0,解得a≥1或a≤-2,即命题q:a≥1或a≤-2;因为命题“p且q”是真命题,所以a=1或a≤-2,即实数a的取值范围是a=1或a≤-2。

48.(1,2]∪[3,+∞)

49.0＜a≤或a≥1 提示:p:0＜a＜1;函数y=lg(ax2-x+a)的定义域为R,等价于∀x∈R,ax2-x+a＞0,则:

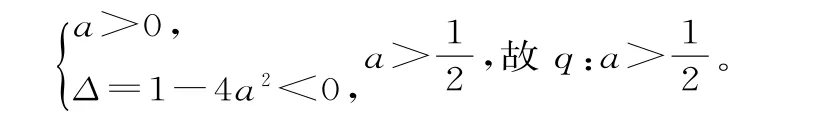
若p∨q为真命题,p∧q为假命题,则p真q假或p假q真,即:

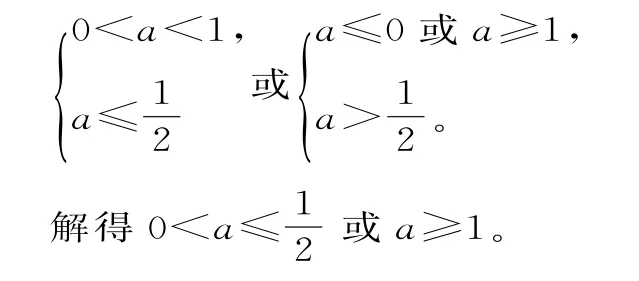
三、解答题

50.逆命题:若x=2且y=-1,则+(y+1)2=0,是真命题。

否命题:若+(y+1)2≠0,则x≠2或y≠-1,真命题。

逆否命题:若x≠2或y≠-1,则+(y+1)2≠0,真命题。

51.(1)这一命题可表述为p:对任意的实数m,方程x2+mx-1=0必有实数根。其否定为﹁p:存在一个实数m,使方程x2+mx-1=0没有实数根。因为该方程的判别式Δ=m2+4＞0恒成立,所以﹁p为假命题。

(2)﹁p:对于所有的实数x,都满足3x≥0。显然﹁p为真命题。

(3)﹁p:若an=-2n+1,则∀n∈N,Sn≥0。﹁p为假命题。

(4)﹁p:所有偶数都不是质数。﹁p为假命题。

52.P={x|a-4＜x＜a+4},Q={x|1＜x＜3}。因为x∈P是x∈Q的必要条件,所以x∈Q⇒x∈P,即Q⊆P。

53.充分性:因为a2+b2=0,所以a=b=0,f(x)=x|x|。

因为f(-x)=-x|-x|=-x|x|,-f(x)=-x|x|,所以f(-x)=-f(x),f(x)为奇函数。

必要性:若f(x)为奇函数,则当x∈R时,f(-x)=-f(x),即-x|-x-a|+b=-x|x-a|-b恒成立。

令x=0,则b=-b,b=0;令x=a,则2a|a|=0,a=0。故a2+b2=0。

54.由(x-a)(x-3a)＜0,其中a＞0,得a＜x＜3a。a＞0,则p:a＜x＜3a,a＞0。

由≤0,得2＜x≤3,即q:2＜x≤3。

(1)若a=1,解得2＜x≤3,若p∧q为真,则,同时为真,即解得pq2＜x＜3,实数x的取值范围(2,3)。

(2)若﹁p是﹁q的充分不必要条件,即q是p的充分不必要条件,则:

55.当命题p为真时,Δ=4a2+4a≥0,得a≥0或a≤-1;当命题q为真时,(a+2)·x2+4x+a-1≥0恒成立,a+2＞0且16-4(a+2)(a-1)≤0,即a≥2。

由题意得,命题p和命题q一真一假。

当命题p为真,命题q为假时,a≤-1;

当命题p为假,命题q为真时,a不存在。

故实数a的取值范围为(-∞,-1]。

56.(1)因为对任意x∈[0,1],不等式2x-2≥m2-3m恒成立,所以(2x-2)min≥m2-3m,即m2-3m≤-2,解得1≤m≤2。即p为真命题时,m的取值范围是[1,2]。

(2)因为a=1,且存在x∈[-1,1],使得m≤ax成立,所以m≤1,即命题q满足n≤1。

因为p且q为假,p或q为真,所以p,q一真一假。

综上所述,m＜1或1＜m≤2。

57.必要性:因为a+b=1,所以b=1-a。

故a3+b3+ab-a2-b2=a3+(1-a)3+a(1-a)-a2-(1-a)2=a3+1-3a+3a2-a3+a-a2-a2-1+2a-a2=0。

充分性:a3+b3+ab-a2-b2=0,即(a+b)(a2-ab+b2)-(a2-ab+b2)=0,(a2-ab+b2)(a+b-1)=0。

又ab≠0,即a≠0且b≠0,故a2-ab+b2=(a -≠0,只有a+b=1。

综上可知,当ab≠0时,a+b=1的充要条件是a3+b3+ab-a2-b2=0。

因为p为真命题,m≥-1。

当p为真命题时,实数m的取值范围为[-1,+∞)。

故q为真命题时,m≤。

(2)因为p∨q为真命题且p∧q为假命题时,所以p、q一真一假。

因为x∈(-∞,0)且＞0,所以＜0,故y=在(-∞,0)上是减函数。

要使f(x)=log)在(-∞,0)上3a是减函数,应满足3a＞1。

(2)由(1)知,若p为真命题,则＜a＜2。

若q为真命题,则函数f(x)=的值域为[0,+∞)。

所以42-20a≥0,解得a≤。

因为p∨q为真命题,p∧q为假命题,所以p、q一真一假。

故实数a的取值范围为 (- ∞,]∪,2)。