求解椭圆最值题方法灵活很容易

■安徽灵璧县黄湾中学 王 晖

最值问题是椭圆中的一个难点,这是因为此类问题覆盖的知识面广,处理问题的方法灵活多变,所需知识的综合性强。下面我们就一起来探究椭圆中的最值问题,希望对提高同学们的解题技能能够有所帮助。

一、基本量的最值

椭圆中的基本量有a,b,c,e,,等 。

解题策略：求解此类问题的常用方法是:(1)建立函数关系,将问题转化为求函数的最值;(2)利用椭圆定义结合图形,将问题转化为点与线的位置关系。

椭圆方程为=1(a＞0),求椭圆离心率e的最大值。

解析：设A2=(a2+1)2,B2=a4+a2+1。

因为A2＞B2,所以椭圆的焦点在x轴上,且C2=A2-B2=(a2+1)2-(a4+a2+1)=a2。则椭圆的离心率e==

当a=,即a=1时,e=

图1

如图1所示,以椭圆的焦点为焦点,过直线l:x-y+9=0上一点P作椭圆,要使所作的椭圆长轴最短,点P应在何处?求出相应的椭圆方程。

解析：由已知椭圆=1,得其焦点为F1(-3,0),F2(3,0),它们也是所求椭圆的焦点,设F1(-3,0)关于直线l:x-y+9=0的对称点为F'(m,n),则由+9=0,解之得m=-9,n=6。

故F'1点的坐标为(-9,6),直线F'1F2的方程为x+2y-3=0,则由方程组解得,。x=-5y=4

故当P点坐标为(-5,4)时,|PF1|+|PF2|最小,此时最小值为2a=65。

故a2=45,又c2=9,b2=36。

二、距离的最值

此类问题包括圆上的点到直线的距离,椭圆上的点到某个定点的距离,也包括距离之和等。

解题策略：考虑到椭圆方程的类型和椭圆的第二定义,常用的求解方法有以下三种:(1)利用椭圆的参数方程,将问题转化为三角形求解;(2)根据椭圆标准方程是二次方程的特点,将问题转化为二次函数求解;(3)利用椭圆的第二定义结合几何知识巧妙求解。

如图2所示,已知点A在圆C:x2+(y-2)2=上移动,点B在以F(0)为右焦点的椭圆x2+ky2=k上运动,求|AB|的最大值。

解析：由c2=k-1=)2,得k=4。

故椭圆方程为=1。|AB|的最大值是椭圆+y2=1上动点B(x,y)到圆C的圆心(0,2)距离的最大值与圆的半径之和。

图2

设B到圆心的距离为d,则有d2=x2+(y-2)2=4-4y2+(y-2)2=-3·

因点B是椭圆上的点,故-1≤y≤1,即当y=时,=

故|AB|max=

图3

已知椭圆方程为=1,一定点P(1,-1),F是椭圆的右焦点,在椭圆上求一点M,使|MP|+2|MF|的值最小。

解析：若是设M(x,y),先求|MP|+2|MF|,再求最小值则很烦琐。若从|MF|联想到椭圆的第二定义,则可使解题过程大为简化,达到简捷获解的目的。

容易求出a=2,c=1,e=。设M在右准线上的射影是N,则根据椭圆的第二定义,可得,即2|MF|=|MN|,故|MP|+2|MF|=|MP|+|MN|。

显然当P,M,N三点共线时,|MP|+|MN|最小。

过P作准线的垂线y=-1,则由方程组解得

已知椭圆的焦点F1,0)和F(-3,0),离心率。求椭圆上的点2到直线2x+3y+8=0的距离的最大值和最小值。

解析：设椭圆上任意一点P(2cosα,sinα),则它到直线2x+3y+8=0的距离为:

三、焦半径的最值

椭圆焦半径是指椭圆上一点到焦点的距离,容易得到焦半径r的取值范围为:a-c≤r≤a+c。解题策略：设P0(x0,y0)为椭圆=1上一点,则左焦半径r1=a+ex0;右焦半径r2=a-ex0,因而有r1+r2=2a。故此涉及椭圆焦半径最值问题常用的求解方法有以下两种:(1)利用基本不等式r1r2≤;(2)转化为关于x0的函数y=f(x0)求解。

椭圆=1上有n个不同点P1,P2,… ,Pn,椭圆的右焦点为F,数列{|PF|}是公差大于的等差数列,则n

n的最大值为( )。

A.199 B.200 C.198 D.201

解析：a=2,c=1,故(PnF)max=a+c=3,(PnF)min=a-c=1。

又PnF=1+(n-1)×d,故(n-1)d≤2,即≥d＞,解得n＜201。

故n的最大值为200,应选B。

如图4所示,A、B是两个定点,且|AB|=4,动点M到A点的距离是6,线段MB的垂直平分线l交MA于点P,直线l'垂直于直线AB,且B到l'的距离为。现以AB所在直线为x轴,AB的中垂线为y轴建立坐标系。

(1)求证:点P到点B的距离与到直线l'的距离之比为定值;

图4

(2)若P点到A、B两点的距离之积为m,当m取最大值时,求P点的坐标。

解析：(1)由题意易知A(-2,0),B(2,0)。

因为|PA|+|PM|=|PA|+|PB|=6,且|AB|=4,所以P点轨迹为椭圆,易求其方程为=1。

因为直线l':x=正好为椭圆的右准线,B(2,0)为右焦点,所以

(2)m=|PA|·|PB|=9,当且仅当PA=PB时,m取得最大值9,此时点P为(0,-5)或(5,0)。

图5

如图5,P为椭圆=1(a＞b＞0)上任一点,F1、F2为其左、右焦点,求点P的坐标,使得|PF1|·|PF2|有最大、最小值。

解析：由椭圆的定义知,|PF1|+|PF2|=2a,又|PF1|+|PF2|≥2,故有|PF1|·|PF2|≤a2。

当且仅当|PF1|=|PF2|,即P(0,±b)时,|PF1|·|PF2|有最大值a2。

又知F1(-c,0),F2(c,0),在△PF1F2中,记∠F1PF2=θ,由余弦定理可得4c2=|PF1|2+|PF2|2-2|PF1|·|PF2|cosθ,即4c2=(|PF1|+|PF2|)2-2|PF1|·|PF2|(1+cosθ)。

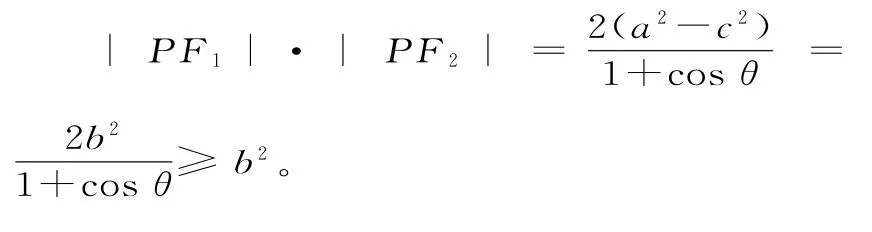
当cosθ=1时,|PF1|·|PF2|的最小值为b2,此时点P的坐标为 (±a,0)。

四、弦长的最值

焦点弦是椭圆众多弦中的一类特殊弦,易知焦点弦的最大值为2a(长轴),最小值为(通径)。

解题策略：求过椭圆上一定点的弦长最值,常用方法是设另一点的坐标为(acosθ,sinθ),将问题转化为三角与二次函数问题;对于斜率一定的弦长最值问题则转化为二次函数问题求解。

过椭圆=1的顶点B(0,-2)作弦AB,求|AB|的最大值。

解析：设点A(3cosθ,2sinθ),则有|AB|2=9cos2θ+(2sinθ+2)2=-5sin2θ+8sinθ+13=-5(si n θ-

故当sinθ时,|AB|的最大值为。

若直线y=x+t与椭圆x2+4y2=4相交于A、B两点,当t变化时,|AB|的最大值为____。

解析：由y=x+t,x2+4y2=4,得5x2+8tx+4t2-4=0,则由弦长公式知:

五、三角形的最值问题

椭圆中三角形类型较多,其中焦点三角形是较特殊的一种,它的周长为定值2a+2c,面积由公式S=b2tan(θ为焦点三角形的顶角)给出。

解题策略：若三角形是焦点三角形,常利用椭圆定义结合基本不等式求解;若是其他三角形,则利用韦达定理转化为函数问题求解。

P为椭圆=1(a＞b＞0)上一点,F1,F2为焦点,当P在什么位置时,△PF1F2的顶角∠F1PF2最大?

解析：设|PF1|=m,|PF2|=n,则:

当且仅当m=n时,即点P处于短轴端点时,(cosθ)=1,即 ∠F1PF2最大。

过椭圆2x2+y2=2的一个焦点F,作直线交椭圆于P、Q两点,求△PQO(O为坐标原点)面积的最大值。

解析：设F为椭圆的下焦点,则直线PQ的方程为y=kx-1。又设P(x1,y1),Q(x2,y2)。

当且仅当t=1,即k=0时,(S△PQO)max

图6

如图6所示,若F是椭圆=1(a＞b＞0)的一个焦点,MN为过其中心的一条弦,求S△FMN的最大值。

解析：不妨设F为右焦点及M(x1,y1),N(x2,y2),则有:

要求S△FMN的最大值,只要求|y1-y2|的最大值。显然|y1-y2|max=2b。

故S△FMN的最大值为bc。