类比思想在立体几何中的应用
2017-04-28 06:38:16郑州市第十一中学1805班赵晨思
中学生数理化(高中版.高二数学) 2017年12期
■郑州市第十一中学1805班 赵晨思
类比思想在数学中有着重要的应用,下面举例分析它在立体几何中的应用。
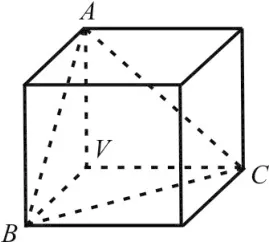
图1
截正方形ABCD的一个角得△ABC,由勾股定理知c2=a2+b2。如图1,把正方形换成正方体,截线AC换成截面ABC,得三棱锥V-ABC,设 △VAB,△VBC,△VAC,△ABC面积分别为S1,S2,S3,S,则在棱锥V-ABC中有结论:S2=。

引用例1中的三棱锥V-ABC,VA、VB、VC与平面ABC所成的角分别为α、β、γ,三者有何关系?平面ABC与平面VAB、平面VAC、平面VAB的夹角分别为α1、β1、γ1,三者有何关系?
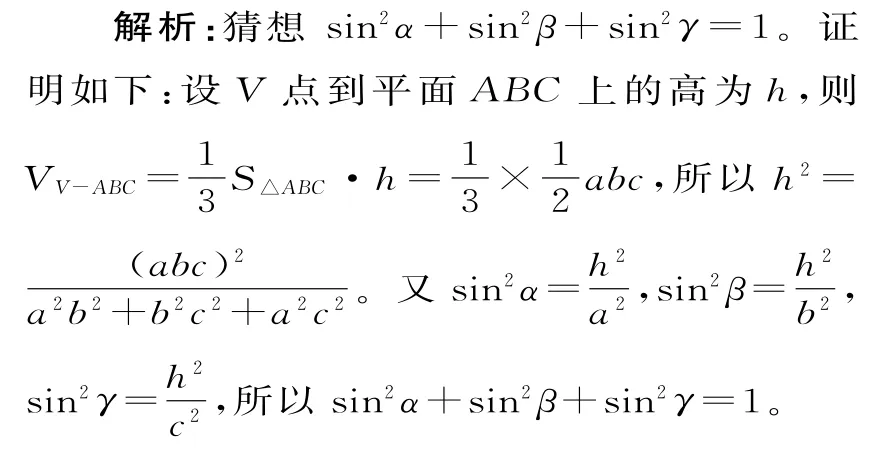
所以cos2α+cos2β+cos2γ=2。
那么,猜想sin2α1+sin2β1+sin2γ1=2。
证明如下:设△VAB边AB上的高为VD,△VBC边BC上的高为VE,△VAC边AC上的高为VF。所以·AB=得VD2
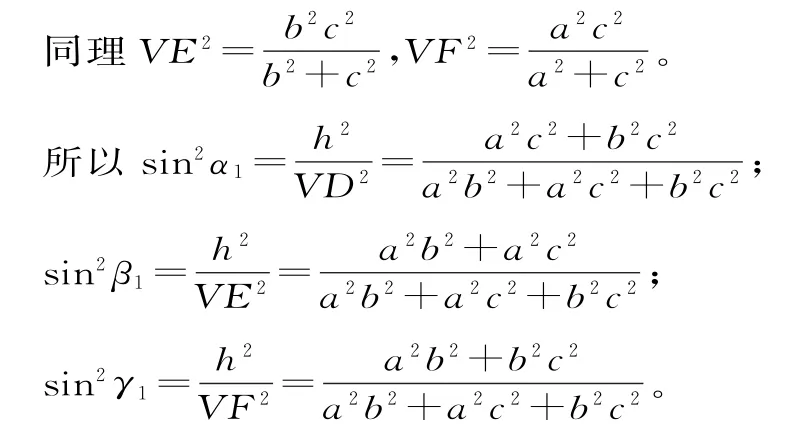
所 以 sin2α1+sin2β1+sin2γ1=2。
在长方体A1B1C1D1-ABCD中,A1B1=a,B1B=h,B1C1=b,体对角线B1D与从B1点发出的三条棱B1A1,B1B,B1C1的夹角分别为α、β、γ,三者之间有何关系?B1D与平面A1B1C1D1的夹角为α1,B1D与平面B1C1CB的夹角为β1,B1D与平面A1B1BA夹角为γ1,探究α1、β1、γ1的关系。
解析:猜 想 cos2α+cos2β+cos2γ=1,cos2α1+cos2β1+cos2γ1=2。
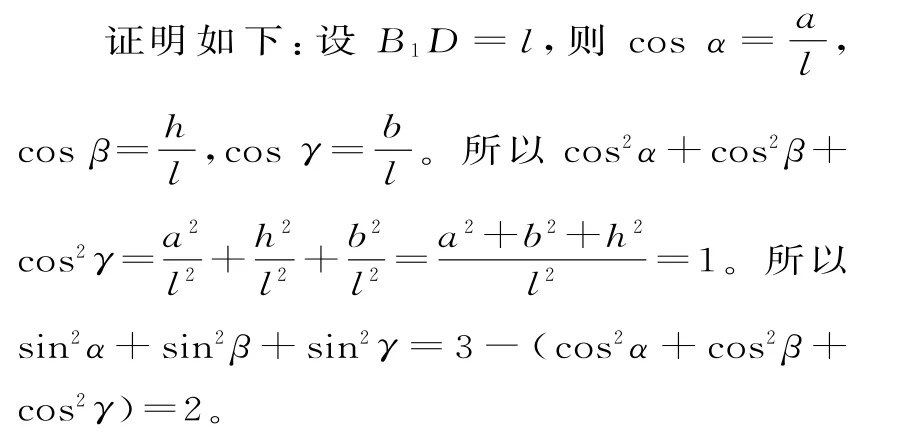
同理,猜想sin2α1+sin2β1+sin2γ1=1,cos2α1+cos2β1+cos2γ1=2。
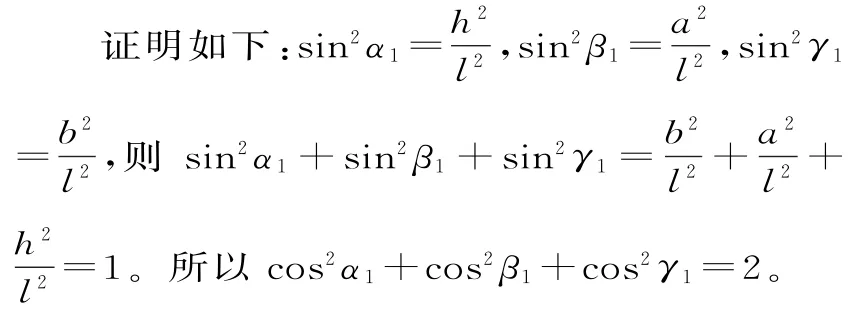
通过这三道例题,我们能够深刻体会到类比思想在立体几何中的应用。
猜你喜欢
中学生数理化·七年级数学人教版(2020年12期)2021-01-18 06:57:42
语数外学习·高中版上旬(2020年8期)2020-09-10 07:22:44
小学生必读(中年级版)(2019年10期)2019-03-24 07:36:00
福建中学数学(2018年1期)2018-11-29 02:52:14
西南石油大学学报(自然科学版)(2018年4期)2018-08-02 05:42:38
速读·下旬(2017年7期)2017-08-03 20:09:44
人间(2016年28期)2016-11-10 22:59:54
广西电力(2016年5期)2016-07-10 09:16:44
理科考试研究·高中(2015年4期)2015-05-19 15:50:44
初中生·考试(2009年5期)2009-06-12 09:46:14

