椭圆知识结构与拓展

■河南南阳市一中 郑书芬

一、知识结构框架

二、实例分析

题型一：椭圆的定义及其简单性质

已知焦点在x轴上的椭圆1的离心率是e,且,则实数m的取值范围为_____。

解：因为椭圆=1的焦点在x轴上,所以0＜m＜2。因为e,所以e。因为所以＜1,解得0＜m所以实数m的取值范围为

点评:求与离心率范围有关的问题,关键是找出a、b、c满足的关系式,然后转化成关于e的方程或不等式进行求解,同时要注意隐含条件e∈(0,1)。

题型二：椭圆的标准方程

椭圆中心是坐标原点,长轴在x轴上,离心率,已知点到椭圆上的点的最远距离是7,求这个椭圆的标准方程。

解：设所求椭圆方程为1(a＞b＞0)。

因为,所以a=2b,于是椭圆方程化为=1。

设椭圆上的点M(x,y)到点P距离为d,则d2=x2+=4b2+y2-3y+=-3+4b2+3。

对f(y)=-3+4b2+3的最值情况进行讨论:

(1)当-b≤-,即b≥时,=4b2+3=7⇒b=1,椭圆标准方程为=1;

(2)当＜-b,即b＜时,=f(-b)=7⇒b=7,与矛盾。

综上所述,当y=时,有=4b2+3=7,b=1。

故所求椭圆方程为+y2=1。

点评:(1)利用离心率确定a与b的关系。(2)利用最值进一步确定b的值。(3)由椭圆方程=1(a＞b＞0)得-b≤y≤2b,由d2=-(y )+4b2+3知d2是y的二次函数,其对称轴为y=,故应就二次函数对称轴与区间[-b,b]的位置关系进行讨论。本题容易在求最值时忽视b的范围而没有加以讨论,导致解题过程出错。

题型三：焦点三角形

设P为椭圆=1(a＞b＞0)上任意一点(不在x轴上),F1,F2为焦点,且∠F1PF2=θ,证明:

(1)△F1PF2的周长为定值2a+2c;

(2)在△F1PF2中,有S△F1PF2=b2·

(3)在△FPF中,有cos1=1-2e2,并且点P在y轴上时θ角的张角最大。

证明：(1)△F1PF2的一边长为焦距2c,另两边的和为定值2a,所以周长为定值2a+2c。

(2)记|PF1|=r1,|PF2|=r2,由椭圆的第一定义得,r1+r2=2a,故(r1+r2)2=4a2。

在△F1PF2中,由余弦定理得-2r1r2cosθ=(2c)2。

配方得(r1+r2)2-2r1r2-2r1r2cosθ=4c2,即4a2-2r1r2(1+cosθ)=4c2。

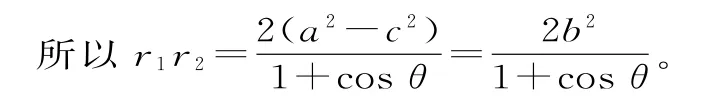
由任意三角形的面积公式得:

(3)设|PF1|=r1,|PF2|=r2,则在△F1PF2中,由余弦定理得:

当且仅当r1=r2,即点P在y轴上时cosθ取得最小值,而角θ取得最大值。

点评:(1)利用椭圆的定义求周长。(2)利用正、余弦定理相结合求解面积。(3)通过本例要掌握以下结论:①椭圆上一点和两焦点组成的三角形叫焦点三角形,有一个角为直角的焦点三角形叫焦点直角三角形;②椭圆中 S△F1PF2=b2tan;③ 在 椭 圆 的△F1PF2中,有cosθ-1=1-2e2,并且点P在y轴上时θ角的张角最大。

跟踪练习：

1.求过点 (),且与椭圆=1有相同焦点的椭圆的标准方程。

由c2=a2-b2可得b2=4,所以椭圆的标准方程为=1。

点评:充分利用椭圆的定义求解。

2.已知椭圆C=1(a ＞b＞0)的离心率为,点 (2 ,2)在C上。

(1)求C的方程。

(2)直线l不过原点O且不平行于坐标轴,l与C有两个交点A,B,线段AB的中点为M。证明:直线OM的斜率与直线l的斜率的乘积为定值。

解：(1)由题意有1,解得a2=8,b2=4。

所以C的方程为=1。

(2)(法一)设直线l:y=kx+b(k≠0,b≠0),A(x1,y1),B(x2,y2),M(xM,yM)。

将y=kx+b代入=1得(2 k2+1)x2+4kbx+2b2-8=0。

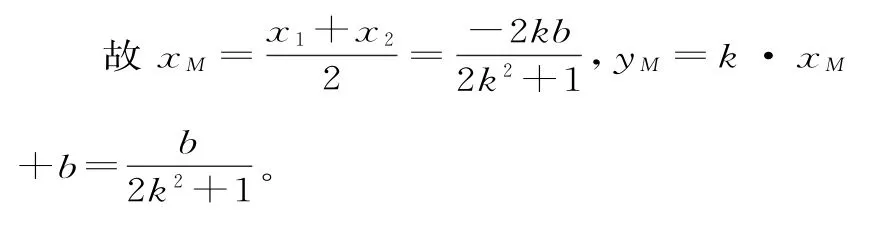
于是直线OM的斜率即k·k=。所以直线OM的斜率与OM直线l的斜率的乘积为定值。

所以直线OM的斜率与直线l的斜率的乘积为定值。

点评:圆锥曲线中的定点、定值、定线问题是高考中的常考题型,难度一般较大,常常将直线、圆及圆锥曲线等知识结合在一起,注重对数学思想方法的考查。解题时可以通过直接推理、计算,并在计算推理的过程中消去变量,从而得到定值。

本题的一般性结论:不过原点O的直线l交椭圆C=1于A,B两点,线段AB的中点为M,则kAB·kOM=