分布式测量体制下的船姿数据重构*

向 颉,茅永兴,李红艳,袁小江

(中国卫星海上测控部,江苏 江阴 214431)

分布式测量体制下的船姿数据重构*

向 颉*,茅永兴,李红艳,袁小江

(中国卫星海上测控部,江苏 江阴 214431)

新一代航天测量船采用的分布式船姿船位测量体制提高了数据的准确性和可靠性，同时也给数据处理与使用提出了更多的需求，比如姿态数据一致性检验、姿态数据联合使用等。为此，提出了一种新的船姿数据重构方法。首先，对集中式与分布式测量机制进行了对比，分析了采用传统数据处理方法解决新需求会产生困难的原因，并指出姿态重构数据的取得将成为解决这些问题的关键；然后，分两个过程对分布式船体姿态测量数据的重构方法进行了推演，并说明了如何使用重构数据去解决新需求；最后，在重构数据本身精度和重构数据对飞行器目标定位精度影响两个方面对该重构方法进行了检验，结果表明使用该方法得到姿态数据满足任务精度指标要求。

航天测量船；姿态测量；分布式测量；姿态矩阵；数据重构

1 引 言

航天测量船的姿态测量精度是影响精度的重要因素[1]。传统测量船的姿态测量系统基于平台惯导和集中式测量体制[2]。集中式测量体制中，目标测量数据必须经过变形的补偿计算，在可靠性和精度方面都有待改进[3-5]。为此，相关研究人员在改进测量方法和测量体制方面做了大量的尝试[6-9]。考虑实际应用效果，新测量船使用基于捷联惯导并保留船体变形测量的分布式设计。

船姿测量设备分布式设计在精度与可靠性方面有着集中式测量体制无可比拟的优势，但也对船姿、变形数据处理使用提出了更多的需求。本文将从分布式姿态测量体制着手，分析使用传统处理方法解决新问题所面临的困境，然后建立一种基于分布式船姿测量体制的数据重构方法，重新构建各测量点的姿态数据，为解决新问题做好技术储备。

2 分布式船体姿态测量

2.1 测量原理

为更清楚地了解分布式姿态测量体制的特点，首先介绍传统的集中式测量体制。图1为集中式测量体制下的设备分布图。

图1 集中式测量设备分布图

如图1所示，惯导1、惯导2互为备份，同时对船体同一点的姿态进行测量。雷达分别布于平台惯导前后两端，雷达与惯导之间的变形量使用光学变形设备测量得出。惯导和雷达的中心点上分别部署了固联的坐标系，飞行器的测量数据通过补偿变形量和姿态量后由各测量坐标系转换至惯导地平坐标系[3]。这种集中式的数据处理方法本质上是在各坐标系中对目标测量数据进行旋转和平移。

图2展示了分布式测量设备的分布情况，与集中式主要的区别为每个测量雷达基座下方安装捷联惯导，能够独立测量雷达所处位置的姿态。该设计减少了处理变形数据的中间环节，提高了可靠性。当船载测量设备基座处的船姿数据正常时，飞行器的测量数据可直接转换至惯导地平坐标系下，其坐标中心在测量设备基座的惯导处；当船姿数据异常时，可使用另一惯导处的船姿量信息经变形修正后(即姿态矩阵传递)，转换至新的惯导地平坐标系下。不难发现在新测量体制下，船体姿态数据不再只有一组数值，而是许多组不同点位的姿态数据，这些船姿数据是否发生漂移、一致性如何检验、数据如何联合使用等一系列新的需求都被陆续提出。

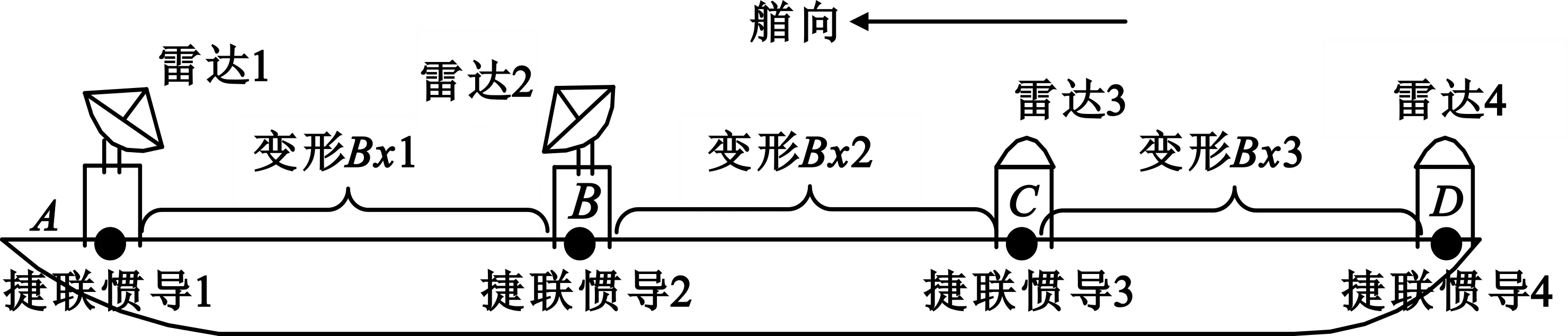
图2 分布式测量设备分布图

2.2 新需求的处理

无论对于数据一致性检验还是数据联合使用，采用传统处理方法都不能给出有效的解决方案。分析集中式姿态数据处理方法不难发现，该方法只能将目标测量数据从一个坐标系转换至另一个坐标系，坐标转换后坐标系中心也会随之改变。因此，产生的数据并非等效数据，不能直接用作数据的检验和融合。

若能得到同一点的姿态量重构数据，那么问题就会变得简单。将同一点的重构值对应至提供数据的惯导设备上，会得到大量的等效数据，数据检验问题和融合计算问题实质上就转化为多传感器冗余测量数据的检验和融合问题。因此，在分布式船姿船位测量体制下有必要建立一种船姿数据的重构方法。

3 分布式船体姿态测量数据的重构

3.1 问题概述

对于图2所示分布式测量系统中的数据重构问题，将其表述为更具一般性的问题：已知点A的姿态测量值为(ψA,θA,KA),点A的船摇旋转矩阵为B(cA)，点A、B间变形已知，其等效旋转矩阵为B(b)，需要使用已知量重构点B的船摇数据(ψB,θB,KB) 。

3.2 解决方法

上述姿态数据重构问题可分为两个子过程解决：过程1，求点B的重构姿态矩阵B(cB)；过程2，求点B的重构姿态数据(ψB,θB,KB) 。

3.2.1 求解点B的重构姿态矩阵B(cB)

修正A点姿态误差的欧拉角旋转矩阵为

(1)

B(cB)=B(cA)B-1(b)=B(cA)BT(b)。

(2)

式(2)为使用点A姿态数据重构出的点B姿态矩阵B(cB)。

3.2.2 重构点B的姿态数据(ψB,θB,KB)

假设通过上述步骤已经求出B(cB)各元素具体数值，并且将式(2)右端展开:

(3)

参考式(3)两端，取其部分元素可将点B的重构姿态值解出，直接给出重构值的表达式：

ψB=arcsinB21，

(4)

(5)

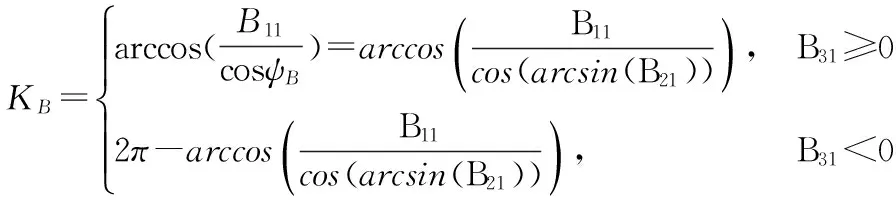
(6)

式(4)～(6)即使用点A姿态数据重构得到的点B姿态数据(ψB,θB,KB)。

至此，对于任意两点，只需已知其中一点的姿态值和两点间的变形值，通过以上步骤就可以完成使用一点姿态数据重构另一点姿态数据的过程。

采用该方法得到大量冗余姿态数据，便可用于数据检验和融合计算问题。对于姿态数据一致性检验，可以将所有惯导输出的姿态数据重构至某一点上，根据测量数据和重构数据的误差方差制定出检测阈值，使用置信度矩阵的方法完成各姿态量的一致性校验[10]。使用冗余姿态重构值也可以完成姿态数据的融合计算，在工程实践中基于最大似然估计的船姿数据融合法也取得了较好的结果[11]。

4 试验数据处理结果

本节分别从重构数据本身的精度和重构数据对飞行器目标测量精度的影响两个方面对分布式船体姿态测量数据的重构方法进行检验。

4.1 船姿重构数据本身精度

在船姿重构数据本身精度检验方面，由于缺乏更高精度的检验标准，本文通过求取相同点位姿态实测值与重构值的残差进行，并分析统计结果。具体数据选用航天测量船海上综合校飞试验数据，结果如图3和表1所示。

(a)平台惯导姿态测量值

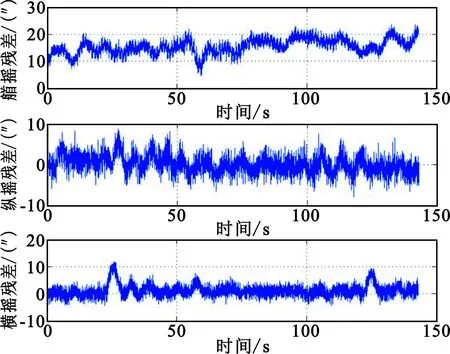
(b)平台惯导姿态重构值残差

(c)捷联惯导1姿态重构值残差

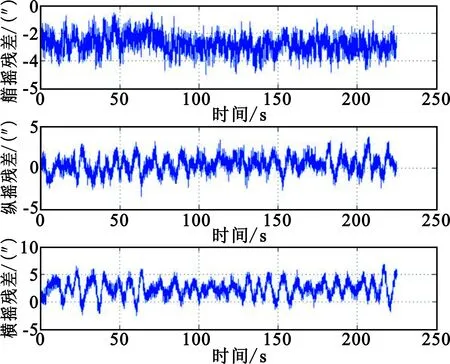
(d)捷联惯导2姿态重构值残差

架次UCBSINS-PINSΔKΔψΔθSINS1-SINS4ΔKΔψΔθSINS2-SINS4ΔKΔψΔθ112.932.74-0.72-2.571.562.67-2.770.422.39215.50.061.17-2.842.212.55-3.342.092.71314.743.920.17-2.842.032.99-2.342.152.6748.060.03-4.12-2.171.413.44-0.680.932.8557.141.92-2.47-2.852.392.08-2.782.542.0566.781.27-2.15-2.982.463.03-2.942.482.58均值10.861.66-1.35-2.712.012.79-2.481.772.54

从图3(b)～(d)中可以看出，重构姿态值与平台惯导实测值的残差要明显大于捷联惯导之间重构产生的残差。特别在艏摇方向上，图3(b)中艏摇残差均值达到12″，因为捷联惯导与平台惯导姿态测量精度存在差异，且随着时间的推移，艏摇方向的系统差会增加。在架次4至架次6中，平台惯导提前校准了艏向值，残差不超过10″。由于捷联惯导测量精度比平台惯导高，图3(c)、(d)中的残差变化范围明显比图3(a)小，且残差曲线呈现平稳随机性。而图3(b)中的艏摇残差随着平台惯导艏摇测量值(见图3(a))的起伏，具有相同的趋势性。从表1可以看出，在姿态量3方向上，捷联惯导2重构残差均值比捷联惯导1残差均值略小，但比平台惯导残差略大(艏摇除外)。在数据重构过程中，平台惯导使用1段变形数据，捷联惯导1使用3段变形数据，捷联惯导2使用2段变形数据，这与残差特性具有较强的关联性。

图3和表1显示了使用姿态量重构方法得到的姿态值与实测值的残差在20″内，每架次结果均值不超过5″(平台惯导艏摇除外)。试验结果并未显示重构值有明显跳变和与实测值偏差较大的情况。

4.2 重构数据对飞行器目标测量精度的影响

在重构数据对飞行器目标测量精度影响方面，考虑了捷联惯导的测量误差和变形测量误差，在某次任务的理论测量数据上进行误差传播的理论计算，比对了实际姿态量误差和姿态量重构值误差对测量目标地平系精度的影响，具体值见表2。

表2 姿态量对测量目标地平系影响

表2中数据显示，姿态量误差对地平系的测量数据影响最显著在Z轴方向，最大至9.8 m。使用重构值计算后的误差影响量级与使用测量值误差影响量级相当。

综上所述，经姿态重构方法计算得到的数据无论是数据本身还是对地平系的测量结果影响，精度均能满足任务要求。

5 结束语

新一代航天测量船引入了分布式捷联惯导系统，同时保留了变形系统，形成了独特的分布式船姿船位测量体制,给航天测量船带来了诸多优势，但也对数据使用方式提出了新的需求。为此，本文从测量船船姿测量体制入手，分析了传统处理方法面临的困境，并分析了船姿数据重构解决问题的可能性，对船姿数据重构方法进行了推演，对重构数据的使用进行了说明，最后采用了测量船海上综合校飞数据和理论数据对方法进行了验证。统计结果表明，该方法计算结果正确，曲线平稳，精度满足任务指标要求。

后续还有两项重要的工作待进一步开展：一是需要对重构的船姿数据进行误差分析，基于该分析分离出船姿部分误差项；二是根据各设备测量精度、重构数据的精度以及雷达所处的不同位置制定出该雷达最优的船姿使用策略。

[1] 简仕龙，费加兵，刘冰，等.航天测量船海上测控技术概论[M] .北京:国防工业出版社,2009：121-126.

[2] 潘良.航天测量船船姿船位测量技术[M] .北京:国防工业出版社,2009：139-158.

[3] 张忠华.航天测量船船姿数据处理方法[M] .北京:国防工业出版社,2009：112-125.

[4] 朱伟康，李辉芬，陈德明，等.提高航天测量船定轨精度的途径[J] .电讯技术,2012,52(5)：658-662. ZHU Weikang,LI Huifen,CHEN Deming,et al.Ways to improve orbit determination precision of space TT&C ships[J].Telecommunication Engineering,2012,52(5)：658-662.(in Chinese)

[5] 易东云，吴孟达. 船姿数据的模型误差与噪声误差分析[J] .导弹与航天运载技术,1998(2)：41-44. YI Dongyun,WU Mengda. Analysis for model error and noise error of ship posture data[J].Missiles and Space Vehicles,1998(2)：41-44.(in Chinese)

[6] 钟林，周海渊. 测姿GPS系统在测量船上的应用[J] .科学技术与工程,2013,13(3)：641-644. ZHONG Lin,ZHOU Haiyuan. Measured pose GPS system on the tracking ship [J] . Science Technology and Engineering,2013,13(3)：641-644.(in Chinese)

[7] 张同双，钟德安，潘良，等. 船用星敏感器姿态测量误差建模与仿真分析[J] .电讯技术,2014,54(2)：218-223. ZHANG Tongshuang,ZHONG Dean,PAN Liang,et al.Modeling and simulation of attitude error model for ship-borne star sensor[J].Telecommunication Engineering,2014,54(2)：218-223.(in Chinese)

[8] 王磊，翟国军，刘雁春，等. 利用双星系统进行船体姿态测量[J] .武汉大学学报，2007,32(6)：527-530.

WANG Lei,ZHAI Guojun,LIU Yanchun,et al.Vessel attitude determination using double-star system [J] . Geomatics and Information Science of Wuhan University,2007,32(6)：527-530.(in Chinese)

[9] 陈建国，邵云生，彭会斌. 船用捷联惯性导航系统研究[J] .船舶,2009(8)：30-33. CHEN Jianguo,SHAO Yunsheng,PENG Huibin. Study of marine strapdown inertial navigation system[J].Ship & Boat,2009(8)：30-33.(in Chinese)

[10] 向颉，茅永兴，薛国虎，等. 置信度检验法在新测量船船姿故障诊断中的应用[J] .飞行器测控学报，2015,34(3)：242-245. XIANG Jie,MAO Yongxing,XUE Guohu. Application of confidence test in attitude fault diagnosis for a new instrumentation ship[J].Journal of Spacecraft TT&C Technology，2015,34(3)：242-245.(in Chinese)

[11] 向颉，张赟，杨磊，等. 新测量船惯导数据融合使用方式研究[J] .测控技术,2015,34(11)：52-55. XIANG Jie,ZHANG Yun,YANG Lei,et al. Research on inertial reference data fusion for new space instrumentation ship[J].Measurement & Control Technology,2015,34(11)：52-55.(in Chinese)

李红艳(1975—) ，女，云南楚雄人，高级工程师，主要研究方向为航天测控总体;

袁小江(1978—),男，陕西勉县人，工程师，主要研究方向为航天数据处理与精度分析。

Reconstruction of Ship Attitude Data in Distributed Measurement System

XIANG Jie,MAO Yongxing,LI Hongyan,YUAN Xiaojiang

(China Satellite Maritime Tracking and Control Department,Jiangyin 214431,China)

The application of distributed ship attitude and position measurement system in the new space tracking ship makes data more reliable and accurate,but requires more for the data processing and application,such as attitude data consistency checking,attitude data combined utilization. To solve above problems,a reconstruction method of ship attitude data is proposed.Firstly,the distributed measurement system is compared with the centralized measurement system. The reason that it′s difficult to meet new demands with traditional data processing method is analyzed. The analysis shows that reconstructing attitude data is the key to these problems. Secondly,the ship attitude data reconstruction method is derived by two processes,and how to use the reconstructed data is explained.Finally,the data reconstruction method is tested from the accuracy of the reconstructed attitude data itself and the impact on the accuracy of target positioning. Results show that the attitude data obtained by the data reconstruction method meets the accuracy requirements in the mission.

space TT&C ship；attitude measurement;distributed measurement;attitude matrix;data reconstruction

10.3969/j.issn.1001-893x.2017.04.019

向颉,茅永兴,李红艳,等.分布式测量体制下的船姿数据重构[J].电讯技术，2017,57(4):480-484.[XIANG Jie,MAO Yongxing,LI Hongyan,et al.Reconstruction of ship attitude data in distributed measurement system[J].Telecommunication Engineering,2017,57(4):480-484.]

2016-07-25；

2016-12-23 Received date:2016-07-25；Revised date：2016-12-23

TN99；TP274

A

1001-893X(2017)04-0480-05

向 颉(1982—)，男，湖南龙山人，2014年于南京理工大学获硕士学位，现为工程师，主要研究方向为航天数据处理与精度分析；

Email:xiangjie100@163.com

茅永兴(1966—)，男，江苏海门人，硕士，研究员，主要研究方向为航天器测控技术及航天器轨道动力学；

Email:myx8282@tom.com

*通信作者：xiangjie100@163.com Corresponding author：xiangjie100@163.com