给学生以舞台 展学生之思考

盛增勇

【摘 要】新课标指出，既要关注学生学习的结果，也要关注学习的过程。学生在解决问题的过程中，教师要给学生提供一个舞台，让学生用文字、符号或其他形式展示自己的思维过程和方法，以便于教师第一时间读懂学生的内心世界、读懂学生的认知过程，以便于师生、生生构筑互动交流平台，促进教学的有效进行。而“过程开展”作为教师了解学生、读懂学生，进行因材施教的重要教学策略，具有丰富的教育意蕴和实践价值，值得一线数学教师深入探讨和研究。

【关键词】小学数学；课堂教学；数学思维；过程开展

“过程开展”主要是指在教师的问题导向或任务驱动的帮助下学生进行积极探索研究的学习活动，即让学生在问题解决中把自己思维过程和方法用文字、符号或图表等表示出来，留下痕迹。笔者通过对研究教学方式的积极实践与探索，深刻体会到新形势下为充分给学生以舞台，展学生之思维“过程开展”的必要性，深切感受到开展“过程开展”存在的问题，并结合平时课堂实践进行了研究与思考。

一、过程开展，直面学生认知现实

教师只有合理运用“过程开展”这个措施，去分析学生、了解学生、研究学生，才能读懂学生的内心世界。

1. 基于学生学习起点，走进学生的内心世界

要想真正促进学生的发展，首先要了解学生的能力。教师可以通过问卷方式，研究学生在学习过程中存在的问题，关注学生的学习困难，满足学生发展的需求。

案例：四年级上册【平行与垂直】

据统计，对于平面上两条直线的位置关系，两线交叉成交点这一特征学生容易抓住，但是对延长之后会不会相交的想象，或者表面上不相交，但延长后可以相交这种位置关系，学生不是很理解。因而如何描述平面上的两条直线的位置关系，让学生能够直观地辨别出相交与平行则是本节内容的教学重点。

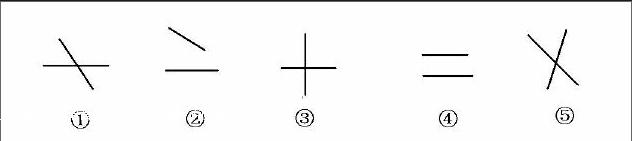
师：根据这两条直线的位置关系，把这五组情况分分类，你觉得怎么分？请你用编号把它们写下来。

生1：我是按两条直线是否相交分①③⑤为一类，②④为一类。

生2：我也是按两条直线是否相交分①②③⑤为一类，④为一类。

师：刚才两位同学都是按照两条直线是否相交这个标准来分类。但分的结果却不相同，看来矛盾都集中在②，它究竟该是相交还是不相交呢？先请把②分到不相交的说一说。

（课件出示图②）

生：①③⑤为交叉在一起，②④没有交叉在一起。

师：似乎有些道理。请把②分到相交的说一说。

生：直线是无限延长的，②两条直线其实延长后能相交的。

师：抓住了直线可以无限延长的特征，怎么看出延长以后会相交？

生：左宽右窄。

师：往哪端延长会相交？会相交在哪里？

课件演示延长动画：

师：这一类中，每组的两条直线都互相交叉，我们就说它们是相交的，相交的这一点就是它们的交点。

（出示图④）

师：这两条直线也是可以无限延长的，能不能也分在这一类呢？

生：不能。

师：为什么？你们是怎么想的？

生：无论怎么延长，都不会交叉。

生：两条线之间的距离是一样的，不会出现一端宽一端窄。

课件演示：

师：④号这组位置有点特殊，现在没有相交，无论怎么延长都不会相交（永不相交），数学上把这两条直线的位置关系叫做互相平行。

师：同学们，在这张纸上任意画出直线，会产生两种位置关系。相交与不相交。

很明显，“过程开展”这一教学手段更符合学生的认知现状，更具有针对性；在教学方式上，更注重数学知识之间的联系与数学规律的探索，更注重在学生思维过程开展的基础上教学，注重学习方法之间的迁移，更能够促进学生的发展。

2. 基于学生学习经验，把握学生的思维过程

“过程开展”可以让学生清晰地看到，对于一个数学问题，自己或他人先是怎么想的、怎么做的，然后又是怎么想的、怎么做的，使数学思维过程清晰可见，条理分明。

3. 基于问题解决策略，直面学生的思维发展

真教育是心心相印的活动，唯独从心里发出来，才能达到人的心灵深处，学生的智慧才能彼此唤醒，学生的思维会被全面激活，数学思维会更灵活，学生的能力才能得到全面发展。在教学中，让学生圈圈画画写写，放手让学生动手解答，留下思考的过程，可以暴露学生解题的全部思维过程，也可以让老师掌握学生的学习情况。在这个过程中，学生的学习积极性更高，解决问题的主动性更强，解决问题的能力也在逐步提高。

二、过程开展，读懂学生认知过程

荷兰数学家弗赖登塔尔说过：“学习数学的唯一正确方法是实行再创造，也就是由学生把本人要学习的东西自己去发现或创造出来。”实践证明，学生以“学”为中心，教学合一，通过学生思维过程的开展，可以使学生获得大量的感性认识。

三、过程开展，构筑互动交流平台

1. 引发冲突，探寻本质

教学中有不少关键点容易引发学生的认知冲突，冲突的发生正是课堂教学的关键所在。这些冲突既有知识方面的，也有思维层面的，简单的提醒或告知很难让学生对知识本质有真正的理解。教师应沿着学生暴露和呈现错误的轨迹，理其源头，对症下药，引导学生在思维过程中思考、比较、修正，让学生在交流互动过程中得出结论，这样学生才能获取对知识本质的真正理解。

2. 引辩悟道，探明真理

史宁中先生认为，基本活动经验是指学生亲自或间接经历了活动过程而获得的经验。没有亲身经历就不可能获得真正意义上的解题策略。这就需要教师以学生的经验为起点，积极创设基于学生数学学习所需要的活动情景，调动他们已有的知识经验，激發学生的活动兴趣，促使他们积极主动参与到数学活动中。教师要给学生提供较为充足的时间和空间，让他们积极、主动地经历探究、交流、内化、反思等数学活动的全过程，提高学生发现问题、提出问题、分析问题和解决问题的能力。