财政教育投入、科技投入与经济增长关系的实证研究——基于VAR模型

（青岛农业大学 经济与管理学院，山东 青岛 266109）

财政教育投入、科技投入与经济增长关系的实证研究
——基于VAR模型

马筱萌，王宝海

（青岛农业大学 经济与管理学院，山东 青岛 266109）

本文在VAR模型的基础上，对1991—2014年我国财政教育投入、科技投入与经济增长的变化趋势进行实证研究。运用Johansen协整检验法得出财政教育投入、科技投入与经济发展有着均衡关系的结论，进而进行了Granger因果关系检验、脉冲响应函数分析和方差分解，结果表明两者之间存在着长期稳定的均衡关系，且相互影响、相互促进。据此，针对目前我国在财政教育投入和科技投入方面存在的问题提出相应的对策。

教育投入；科技投入；经济增长；VAR模型

一、引言

伴随着我国经济迅猛发展，教育与科技的发展已经成为实现经济增长不可忽视的一部分。在如今经济快速增长的背景之下，教育已成为实现经济增长的主要因素之一，同时又是提升人力资本竞争力的重要途径。教育投入的增加使得对人力资本的投入大大提高，从而提高了劳动生产率，因此带动了我国经济的增长。我国2013年和2014年教育投入占国内生产总值的比重分别为4.30%、4.15%。

近年来我国越来越重视科学技术的作用，科学技术现已成为促进我国经济增长的重要部分之一。“科学技术是第一生产力”，财政科技投入的增加能够促使生产力的提高，近而带动经济的发展。相反，经济发展的好坏决定着科学技术的投入能力，也就是说经济的发展是科学技术的物质基础。我国在2013—2015年科学技术投入占国内生产总值的比重分别为2.09%、2.09%、2.10%。

随着我国经济的飞速发展，学者们对财政教育投入与经济增长、科技投入与经济增长这两者之间的关系做了比较深入的研究，这两者之间的关系也是近年来国内学术界关注的焦点之一，国内也形成了很多学术成果。但是学者们因对数据跨度的选择，采用的计量经济方法的不同，得到的结论也有差别。

在财政教育投入与经济增长方面，国外学者Barro（1991）通过比较分析证明，人均GDP增长的重要原因在于不断增加教育投资[1]。国内学者们对财政教育投入和经济增长这两者之间的因果关系目前还没有统一的定论。一种观点认为财政教育投入与经济增长互为因果关系，学者们通过实证分析，对财政教育投入与经济增长之间的关系进行剖析。周英章、孙崎岖（2002）[2]、覃思乾（2006）[3]通过计量经济学中的模型得出我国教育投入与经济增长之间互为格兰杰因果关系，且长期存在着协同互动的均衡关系。邓媛、李瑞光（2009）[4]，肖小虹（2010）[5]，李兴江、高亚存（2012）[6]，牛晓耕、曹楠楠、白仲夏（2014）[7]运用计量分析的方法分别对云南省、贵州省、甘肃省、河北省教育投入对经济发展的影响进行了深入的分析，结果表明我国财政教育投入与经济增长互为因果关系。另一种观点认为财政教育投入与经济增长之间存在着单向因果关系。毛洪涛、马丹（2004）论证了高等教育投入与经济增长之间存在着单向因果关系，即经济增长是高等教育发展的原因[8]。以王欣和张娟（2010）为代表的学者在研究后认为财政教育是因，而经济发展是其必然结果[9]。在教育投入对经济增长的贡献率研究方面，刘盼盼、赵楠（2015）通过多元回归分析法对2000—2011年间的我国三个地区的数据进行分析，得出财政教育投入对全国、东部、中部、西部经济增长的贡献率分别为58%、66%、69%、49%[10]。

而对于科技投入与经济增长之间的关系，国内外学者们同样也做了许多研究。国外学者Griliches（1986）分析了美国约1000家最大制造企业1957—1977年的数据，研究发现：在生产力的提高方面，科技的支出有着重要的作用，而其中R&D支出的作用更加重要[11]。Jaffe、Trajtenberg和Fogarty（2000）认为R&D投入不仅会促进本产业的技术进步，而且有助于提高其它产业的劳动生产率，从而提升经济体的生产率水平[12]。国内学者王海鹏、田澎、靳萍（2005）[13]，陈志昂、胡贤龙（2011）[14]运用VAR模型，选取不同样本区间数据考察了我国财政科技投入与经济增长这两者之间的相互关系，研究发现我国财政科技投入与经济增长这两者之间有着非常明显的双向因果关系，财政科技投入会在很大程度上带动我国经济的增长，与此同时经济的增长也促进了国家财政科技的投入。在财政科技投入对经济增长的贡献率研究方面，刘拓、傅毓维（2008）测算了1979—2006年间国家财政科技投入对经济增长的贡献率平均值为12.66%[15]。以郑华裔（2009）为代表的专家学者通过协整理论对我国财政科技投入与经济增长之间存在的关系进行了剖析，结果表示：中国财政科技投入和经济增长这两者之间存在着单向因果关系，即科技投入能够促进经济的增长，但是经济增长却对科技投入没有贡献作用[16]。

从以上的研究成果中可以看出，国内外专家学者研究证明了财政教育投入、科技投入对经济增长都有着不可替代的作用。但在以往的研究当中，学者们都是以财政教育投入和财政科技投入其中一个变量为自变量，分别研究一个变量与经济增长的关系。很少有学者将财政教育投入、科技投入和经济增长这三个变量放在一起研究。本文是在前人研究的基础上，运用VAR模型，利用1991—2014年度的数据对教育投入、科技投入与经济增长这三因素之间的关系进行实证分析，得出三者之间所存在的关系。

二、模型变量选取

向量自回归模型（Vector Auto-regression Model，VAR）是一种非结构化的模型，即变量之间的关系并不是以经济理论为基础的。VAR模型实质上是考察多个变量之间的动态互动关系，把系统中每一个内生变量作为所有变量滞后项的函数来构造回归模型，一般形式如下所示：

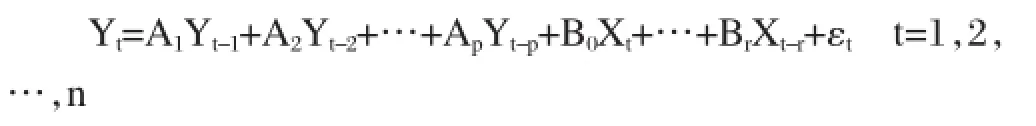
其中，Yt是k维内生变量，Yt-i（i=1，2，…p）是滞后内生变量向量，Xt-i（i=0，1，…r）是d维外生变量向量或滞后外生变量向量，p，r分别是内生变量和外生变量的滞后阶数，Ap是k×k维系数矩阵，Br是k×d维系数矩阵，εt是由k维随机误差项构成的向量。

为了分析财政教育投入、科技投入与经济增长三者之间的关系，本文采用1991—2014年的数据作为样本，所有数据均来自《中国统计年鉴》。研究变量选取国内生产总值、财政教育投入以及科技投入。国内生产总值GDP作为衡量中国经济增长的指标，本文用y来表示。财政教育投入是指国家对教育经费及其他相关教育资源的资金投入，本文用jy来表示。科技投入是支持开展科技活动的投入，也是生产性的投入，本文用kj来表示。为了使数据具有可比性，并考察我国财政教育投入、科技投入与实际经济增长的效应，本文的数据是剔除价格指标后的数据，为了消除可能存在的原始变量的异方差影响，对这三个指标序列进行对数化处理，分别用lny、lnjy、lnkj来表示。

三、实证分析

1、单位根检验

在建立VAR模型和进行协整分析之前，需要对原变量序列进行单位根检验，判断序列的平稳性。如果序列为平稳序列，则可以继续建立模型；如果序列非平稳则需要差分后平稳，否则不可以使用。本文采用ADF单位根检验方法，检验lnjy、lnkj和lny三个时间序列的稳定性，检验结果如表1所示。

表1 各变量的平稳性检验

表2 滞后阶数判断结果

由表1中检验结果可以看出，在5%的显著性水平下，lnjy、lnkj和lny的检验值都大于临界值且概率p值都大于0.05，不能拒绝原假设，序列存在单位根，这三个序列为非平稳序列；对这三个序列进行一阶差分后，dlnjy、dlnkj和dlny的检验值仍都大于临界值且概率p值都大于0.05，不能拒绝原假设，序列存在单位根，这三个序列为非平稳序列；继续对这三个序列进行二阶差分后，ddlnjy、ddlnkj和ddlny的检验值都分别小于临界值且概率p值都小于0.05，接受了原假设，序列不存在单位根，即为平稳序列。因此，lnjy、lnkj和lny的二阶差分可能存在协整关系，可以进行协整检验。

2、VAR滞后阶数的确定

在运用Johansen协整分析方法来检验它们之间是否存在协整关系之前，还要确定VAR模型的最佳滞后阶数。本文对最佳滞后阶数的选择是根据AIC、SC和HQ信息量取值最小准则来确定的。

表2中给出了从0到3阶的VAR模型的LR、FPE、AIC、SC和HQ的值，并以“*”标记出依据相应准则所选择出来的滞后阶数。可以看到，有超过一半的准则选择出来的滞后阶数为1阶，由此可以将此VAR模型的滞后阶数定义为1阶，所以建立VAR（1）模型是比较合理的。

为了检验模型VAR（1）的稳定性，需计算VAR（1）模型差分方程的特征根，并得出其位置分布图。对于滞后期长度为1且有3个内生变量的VAR模型，特征根多项式有3个特征根。此VAR的所有的特征根的倒数的膜小于1，位于单位圆内，所以此VAR模型是稳定的。

3、协整检验

图1 Inverse Roots of AR Characteristic Polynomial

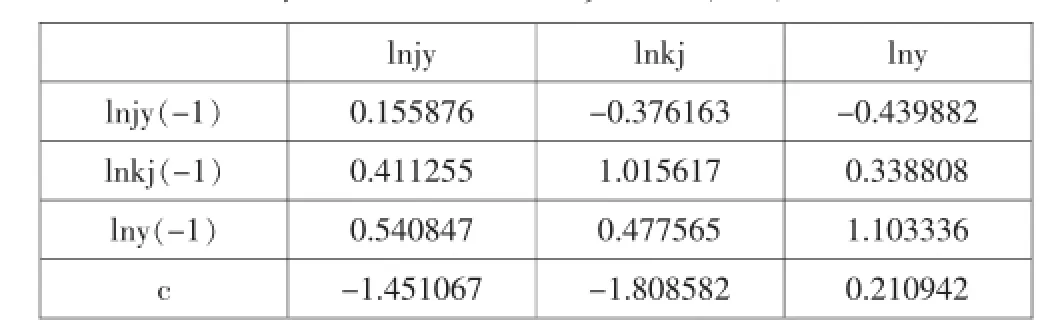
表3 VAR模型的参数估计结果

为了检验财政教育投入、科技投入与经济增长这三者之间是否存在长期的动态关系，本文利用Jahansen协整检验法对三个序列是否存在协整关系进行更具体的检验。如果这三个变量存在协整关系，那么说明这三个变量存在长期的关系。检验结果如表4所示。

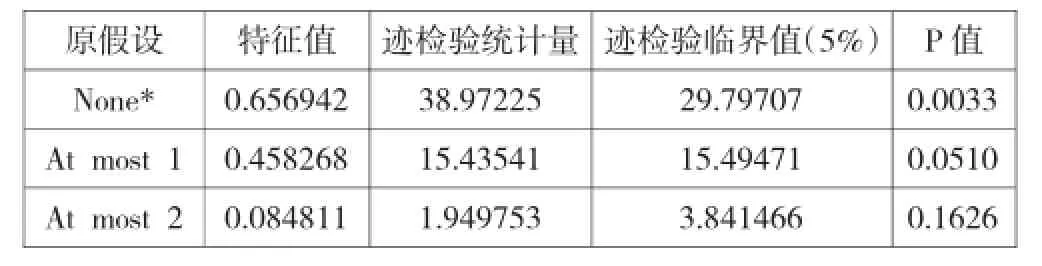
表4 Jahansen协整检验结果

从表4中可以看出：Jahansen协整检验在5%的显著水平上模型存在且只有一个协整关系。这说明财政教育投入、科技投入与经济发展有着均衡关系。

4、格兰杰因果关系检验

格兰杰因果关系实质上是利用VAR模型来进行一组系数显著性检验。格兰杰因果关系可以用来检验某个变量的所有滞后项是否对另一个或几个变量的当期值有影响。上述协整检验结果证明，财政教育投入、科技投入与经济增长之间存在着长期稳定的均衡关系，但这种均衡关系是否构成因果关系，还需要进一步的验证。检验结果如表5所示。

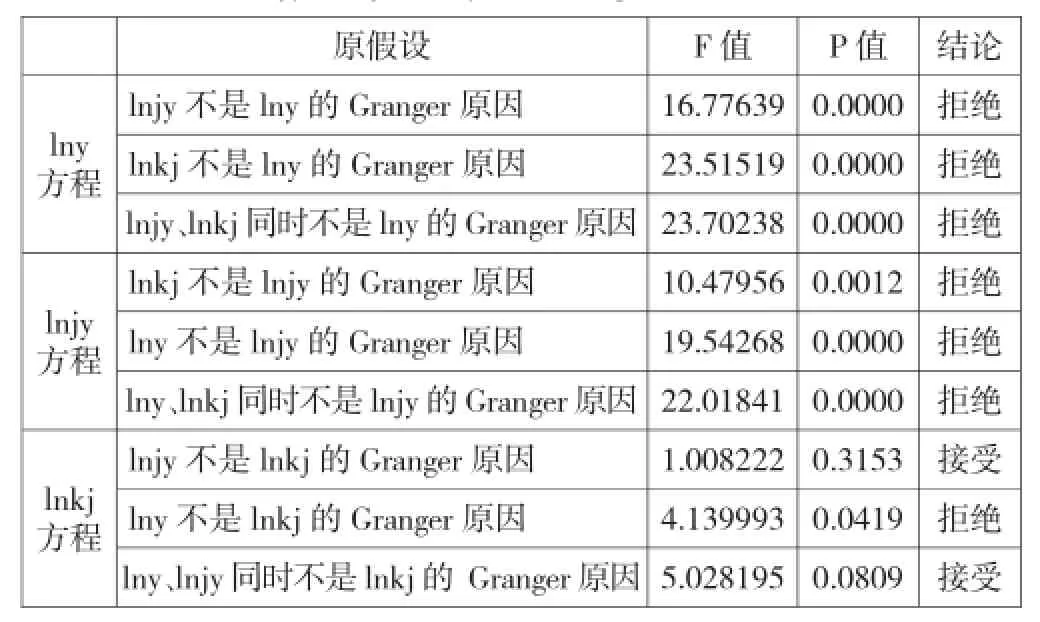
表5 lnjy、lnkj和lny的Granger因果关系检验

由检验结果可以看出：从lny方程来看，拒绝lnjy不是lny的Granger原因的原假设，即教育的投入对经济增长有促进作用。拒绝lnkj不是lny的Granger原因的原假设，说明科技的投入对经济的增长具有显著的Granger影响。两者的联合检验拒绝lnjy、lnkj不能同时Granger引起lny原因的原假设，即财政教育的投入与科技的投入联合促进了经济的增长。

从lnjy方程来看，拒绝lnkj不是lnjy的Granger原因的原假设，即科技的投入对教育有促进作用。拒绝lny不是lnjy的Granger原因的原假设，说明经济的增长对教育的投入具有显著的Granger影响。两者的联合检验拒绝lny、lnkj同时不是lnjy的Granger原因的原假设，即经济的增长与科技的投入联合促进了教育的投入。

从lnkj方程来看，不能拒绝lnjy不是lnkj的Granger原因的原假设，即接受教育的投入对科技没有促进作用的原假设。拒绝lny不是lnkj的Granger原因的原假设，说明经济的增长对科技的投入有显著的Granger影响。两者的联合检验不能拒绝 lny、lnjy同时不是 lnkj的Granger原因的原假设，即经济的增长与教育的投入不能联合促进科技的投入。

5、脉冲响应函数分析

脉冲响应函数可以刻画每个内生变量的变动或冲击对它自己及所有其他内生变量产生的影响作用。第i个内生变量的一个冲击不仅直接影响到第i个变量，而且通过VAR模型的动态结构传递给其他的内生变量，脉冲响应函数试图刻画这些影响的轨迹，显示任意一个变量的扰动是如何通过模型影响所有其他变量，最终又反馈到本身的过程。图2中的横轴表示冲击作用的滞后年数，在模型中将信息冲击作用的滞后年限设定为10年，纵轴表示脉冲响应函数大小。

图2 Response of LNJY to Cholesky One S.D.Innovations

图2反映了财政教育投入lnjy、科技投入lnkj、经济增长lny分别变动一个标准差对财政教育投入lnjy的脉冲函数图。从图2中可以看出，财政教育投入lnjy对来自于自身标准差的冲击表现出递减的正向响应，从第一期到第六期一直递减，从第七期开始日趋平稳，直到第十期达到1.8%左右；经济增长lny从第一期开始对财政教育投入的促进作用一直处于上升阶段，从第八期开始趋于平稳；科技投入lnkj从第一期开始也一直促进财政教育投入，直到第十期达到7.4%左右。

图3反映了财政教育投入lnjy、科技投入lnkj、经济增长lny分别变动一个标准差对经济增长lny的脉冲函数图。从图3中可以看出，科技投入lnkj对经济增长lny的正向冲击作用最大，从第一期开始对经济增长的促进作用不断上升，从第五期开始这种促进作用逐渐趋于平稳，达到5.5%左右；经济增长lny对其自身的冲击作用从第一期开始就一直小幅度上升，在第五期达到最高值1.5%左右，随之对自身的冲击又小幅度减小，在第十期达到1.4%左右；财政教育投入lnjy对经济增长的正向冲击没有科技投入lnkj明显，随着滞后期的增加，财政教育投入对经济增长的正向冲击在缓慢增加，在第十期达到1.3%左右。

图3 Response of LNY to Cholesky One S.D.Innovations

图4 Response of LNKJ to Cholesky One S.D.Innovations

图4反映了财政教育投入lnjy、科技投入lnkj、经济增长lny分别变动一个标准差对科技投入lnkj的脉冲函数图。从图4中可以看出，财政教育投入lnjy变动一个标准差对科技投入lnkj有逐渐下降的正向冲击，随着滞后期的增加，在十期达到1.9%左右；科技投入lnkj对自身的正向冲击作用最大，第十期响应大约为7.9%左右；经济增长lny给科技投入lnkj带来正面的影响，随着滞后期的增加，经济的增长对科技投入的冲击逐渐趋于平稳，第十期达到了1.96%左右。

6、方差分解

方差分解是研究VAR模型动态特征的方法，其主要是将VAR模型中每个外生变量预测误差的方差按照其成因分解为与各个内生变量相关联的组成部分，即分析每个信息冲击对内生变量变化的贡献度，从而了解各新息对模型内生变量的相对重要性。

从表6中可以看到，在第一期的预测中，经济增长的方差主要是由财政科技扰动所引起的，其次是由于自身扰动所引起的。在第四期预测中，经济增长预测方差有83.24%的部分是由财政科技投入扰动引起的，只有4.23%是由于财政教育投入所引起的。随着滞后期的增加，经济增长预测方差中由财政科技投入这一变量扰动所引起的部分增加，而由财政教育投入以及自身扰动引起的部分在逐渐减小，但财政教育投入对经济增长的扰动在第七期开始有小幅度的增加。

表6 变量lny方差分解结果

四、结论及对策建议

1、结论

本文根据我国1991—2014年的数据，基于VAR模型对经济增长、财政教育投入、科技投入的时间序列的动态关系进行了实证分析，可得出如下的基本结论。

第一，经济增长、财政教育投入及科技投入三者的时间序列经过二阶差分后都具有平稳性，同时通过Jahansen协整检验在5%的显著水平上存在且只有一个协整关系。

第二，根据格兰杰因果关系得出：从长期来看，财政教育投入、科技投入对经济的增长具有显著的Granger影响，同时它们之间是双向的Granger因果关系。这表明，教育投入、科技投入对经济的增长都有影响，同时经济的增长也会促进教育和科技的投入。

第三，从脉冲响应函数图可以看出：财政科技投入对经济增长的促进作用比财政教育投入对经济增长的促进作用明显。

第四，从方差分解表可以看出：经济增长预测方差主要是由财政科技投入这一变量扰动所引起的。

2、对策建议

本文研究证明了我国的财政教育投入、科技投入与经济增长互为因果关系，并且教育与科技的投入对经济的发展都具有促进作用。因此，要保证充分发挥我国财政教育投入、科技投入和经济增长的相互作用，为此提出了以下对策建议。

（1）建立多元化的投资融资模式。我国在教育经费投入方面应当采用以国家财政投入为主要来源，以社会捐赠、校企办学为辅的多元化的投资融资模式，以此来弥补我国财政教育投入的缺陷。高等教育是各类教育中最具有专业性与针对性的一类教育模式，所以应该不断提高高等教育教学的质量，为社会经济的发展提供合格的高级专业性人才。我国高校应当加强校企合作，调动那些实力较强、资金充裕的企业单位与各大高校互动合作的积极性，采取“谁投资谁受益”的原则。这样能够使高校科研成果产业化，为高校的发展注入资金，而且能够促进高校培养投资企业紧缺的人才，引导教育人才的定向培养，进而促进教育的发展。

（2）加大对职业技术教育的投资力度。我国应当优化教育投入的结构，以普及义务教育为基础，加大国家财政方面对职业技术教育的投入力度，以此来培养高素质的劳动者。高素质劳动者是经济发展的核心，而对他们的培养又离不开教育。职业教育是为了培养熟练的产业工人，这部分人将直接决定生产过程中的生产效率和技术革新的进程。所以应当努力加大对职业教育的投入力度，促使劳动者的素质提升，这样就可提高全社会劳动生产率，从而实现经济的顺利、稳定增长[18]。

（3）加快科技成果转化。系统转型升级离不开科技成果的转化。我国应当大力扶持科研院所及高校开展科技成果的转化。组织高校和科研院所梳理科技成果资源，发布科技成果目录，建立面向企业的技术服务站点网络，实现自身的研发的科技成果与企业的有效对接，通过研发合作、技术转让等多种形式，最终实现科技成果市场价值。

（4）完善科技投入管理体系。要不断完善科技投入管理体系，充分发挥政府财政科技支出对企业科技研发方面的引导作用，确保每一分钱都用在最需要的地方。应设立一个有关于财政科技投入经费的绩效评价体系，以此来保证财政科技经费能够合理使用。这样才能在财政科技投入总量有限的前提下，使科技研究经费的使用效率达到最优。从而有效地促进科学研究和技术创新的发展，提升国家的整体科学技术水平，使科学技术真正地成为促进经济发展增速的重要手段[19]。

[1] Barro，Robert J.Economic Growth in a Cross Section of Countries[J].The Quarterly Journal of Economics，1991（5）.

[2] Sanders J.Does spending on higher education drive economic growth？20 Years of evidence reviewed[M].Gold water Institute Policy Report，2003.

[3] 周英章、孙崎岖：我国教育投入对实际经济增长的贡献实证分析[J].中国软科学，2002（7）.

[4] 覃思乾：中国教育投入与经济增长[J].统计与决策，2006（16）.

[5] 邓媛、李瑞光：基于VAR模型实证分析云南省教育投入与经济增长的关系[J].技术经济与管理研究，2009（4）.

[6] 肖小虹：贵州经济增长与教育投入的实证分析[J].财经问题研究，2010（8）.

[7] 李兴江、高亚存：甘肃省财政教育投入与经济增长关系的实证分析[J].财会研究，2012（3）.

[8] 牛晓耕、曹楠楠、白仲夏：教育财政投入与经济增长关系的实证检验——以河北省为例[J].中小企业管理与科技（中旬刊），2014（6）.

[9] 毛洪涛、马丹：高等教育发展与经济增长关系的计量分析[J].财经科学，2004（1）.

[10] 王欣、张娟：山西省教育投入与经济增长关系的实证研究[J].山西财政税务专科学校学报，2010（5）.

[11] 刘盼盼、赵楠：我国教育投入对经济增长的实证分析[J].中国市场，2015（12）.

[12] Griliches，Z.，Productivity，R&D and Basic Research at the Firm Level in the 1970s [J].American Economic Review，1986，vo1.76（June）.

[13] Jaffe，A.，Trajtenberg，M.，Fogay，M. Knowledge Spillovers and Patent Citations：Evidence from a Survey of Inventors[J]. American Economic Review，March，2000，90（2）.

[14] 王海鹏、田澎、靳萍：中国科技投入与经济增长的Granger因果关系分析[J].系统工程，2005（7）.

[15] 陈志昂、胡贤龙：我国科技投入与经济增长关系的实证分析[J].山东经济，2011（1）.

[16] 刘拓、傅毓维：我国科教投入对经济增长贡献率实证分析：1979—2006[J].科学管理研究，2008（5）.

[17] 郑华裔：我国财政科技投入和经济增长关系的实证分析[J].现代经济（现代物业下半月刊），2009（10）.

[18] 林丽玲：我国财政教育投入与经济增长关系的实证研究[J].内蒙古煤炭经济，2015（12）.

[19] 范柏乃、江蕾、罗佳明：中国经济增长与科技投入关系的实证研究[J].科研管理，2004（5）.

（责任编辑：刘冰冰）