基于核与灰度的区间灰数多属性群决策方法*

李艳玲，殷新丽，杨 剑（火箭军工程大学，西安 710025）

基于核与灰度的区间灰数多属性群决策方法*

李艳玲，殷新丽，杨 剑
（火箭军工程大学，西安 710025）

针对属性值为区间灰数且专家权重未知、属性权重部分已知的不确定多属性群决策问题，提出了一种基于区间灰数的核和灰度的决策方法。给出了区间灰数的基于核和灰度的简化形式，充分利用区间灰数的核和灰度的信息建立优化模型求得属性的权重。在求出属性权重的基础上，运用灰色关联方法分别求取各专家的核与灰度距理想方案值的关联系数，综合两者得到专家权重，最终综合专家意见并对方案比较排序得出最优结果。鉴于此，提出一种基于区间灰数相对核与灰度的决策方法。最后以一个算例验证该方法的有效性和可行性。

区间灰数，多属性群决策，核，灰度

0 引言

由于事物的复杂性以及人类认识的模糊性，不确定多属性决策问题广泛存在于经济、管理、军事和工程等诸多领域。在传统的决策方法中，决策数值通常是确定的数值。与现实情况相比，具有一定的差别。决策者通常无法给出效果测度以及专家权重、指标权重的具体数值，给出的是一个决策区间范围，相应的决策问题具有着不确定性，是传统的确定性决策所无法解决的。故对不确定性多属性决策具有重要意义。灰色系统理论是邓聚龙老师创立的用于解决现实世界中不确定多属性决策问题的一种方法。灰数尤其是区间灰数的运算、排序是灰色系统理论基础，备受专家学者关注［1-4］。从现有文献看，研究灰数的方法借鉴区间数，而区间数与区间灰数存在差别。文献［5］研究的是用区间数间的比较，并排序，背离了区间灰数的本质。文献［6］给出了标准区间灰度的比较和运算法则，但仅是对几种特殊情形进行比较。文献［7］构建了基于区间灰数相离度的灰色关联系数以及关联度，对决策属性值为区间数且权重信息部分已知的灰色多属性群决策问题进行排序。文献［8］提出了标准灰数、灰数的核和灰度的概念，建立了区间灰数的额运算公理、运算法则以及灰代数系统。而运用此方法去解决专家权重未知以及指标权重未知情况下的不确定多属性决策问题，则比较少。为此，本文首先引入区间灰数的核与灰度的定义，给出了区间灰数的简化形式，定义了标准区间灰数，将决策矩阵转化为标准灰数的简化形式。在此基础上，运用灰色关联度求取专家们的关联系数，并求得专家权重。建立非线性规划模型，分别求得基于核与灰度的权重，由此得出属性权重。根据专家权重与属性权重，可以得出方案的综合评价值，根据区间灰数的相对核和精度的排序方法，进行排序并选择最优方案。

1 基本概念和定义

命题1 对于区间灰数而言，其简化形式既包含区间灰数上限和下限的信息，又与区间灰数一一对应，即区间灰数的简化形式与原区间灰数具有同等的信息量。给定区间灰数，按照核和灰度的定义可以分别计算出核和灰度，即可得区间灰数的简化形式；反过来，当简化形式已知时，可以根据核确定区间灰数核的中心位置，同时根据灰度计算出区间灰数的测度，进而得到区间灰数取值的上限和下限，从而得到区间灰数，区间灰数与其简化形式一一对应［8］。

公理1 两个灰度不同的区间灰数进行和、差、积、商运算时，运算结果的灰度不小于灰度较大的区间灰数的灰度［8］。

灰数的运算法则可以推广到有限个灰数进行和、差、积、商运算的情形。当若干个区间灰数进行运算时，首先对核作相应运算，然后按照取大准则得到运算结果的灰度，从而可得运算结果的简化形式。区间灰数是由区间灰数的核和区间灰数的灰度两个因素决定的，因此，区间灰数的比较既要考虑到核也要考虑到灰度。下面给出标准灰数的相对核的概念。

当区间灰数的灰度为零时，区间灰数的比较就转化为实数之间的比较。

2 基于核和灰度的区间灰数多属性决策模型

2.1 问题描述

设不确定多属性决策问题有m个决策方案集为S=（s1，s2，…，sm），n个评价指标组成的属性值为的C={c1，c2，…，cn}。属性权重为w=（w1，w2，…，wn），其中wjL≤wj≤wjU，0≤wjL≤wjU≤1且。决策者在指标j下对方案i的评价值为区间灰数，其中xijL和 xijU分别为方案si在指标cj下的效果样本值的下限和上限。专家l={1，2，…，k}对方案集S对指标集C的效果样本矩阵为（uijl）m×n。

2.2 指标权重确定

由下面的规划模型M1可以求得基于核的权重。

由下面的规划模型M2可以求得基于灰度的权重。

设由规划模型M1求得的基于核的权重向量为w'=（w'1，w'2，…，w'n），由规划模型M2求得的基于灰度的权重向量为w''=（w''1，w''2，…，w''n），则综合权重为w=（w1，w2，…，wn），其中wj=βwj'+（1-β）wj''（0＜β＜1），则专家l的方案集的综合属性值为。

2.3 专家权重确定

由2.2节求出的综合属性权重wj，利用以下方式集结方案综合核与半径:

通过计算第l个决策者给出的属性值与核正理想方案的灰关联系数，得到决策者权重。第l个决策者给出的属性值与核正理想方案属性值之间的灰关联系数为

故第l个决策者综合关联系数为:

将决策者权重代入属性权重计算公式，重新计算综合属性权重wjl，最后，计算方案的综合核评价值为

运用相应的排序方法进行比较和判断。

3 算例分析

为了说明本文提出的模型及排序方法的有效性。下面给出一个实际例子。某国家国防部拟发展一种导弹武器装备，研制部门提供了4种新型导弹。该国防部派出的专家组对4种导弹的战术技术指标进行了详细考察，考察表如下，问应选择哪一种导弹性能最佳。

针对4种型号B=（B1，B2，B3，B4）的导弹，导弹属性选取主要有:命中精度、弹头载荷、机动性能、价格以及可靠性、可维修性。

以下矩阵列表示表示导弹的属性值，矩阵行分别表示4位专家。Bij（l）表示在第l位专家对i型导弹第j个属性值的区间灰数。

第1步:根据调查所对应的各能力指数，可建立评价值样本矩阵如下:

转换为基于核和灰度的决策矩阵为:

第2步:且属性值范围为:

由规划模型M1求得的基于核的权重向量为:

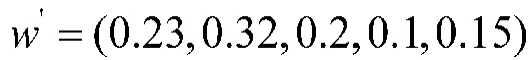
由规划模型M2求得的基于灰度的权重向量为:

取β=0.5，得到属性值的综合权重为:

第3步:由第1步得到的属性权重加权得到每位专家对各个方案的综合属性值为:

故得到核正理想方案为:

专家与核正理想的关联系数为:

专家与灰度正理想的关联系数为:

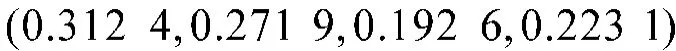
即专家权重为:

第4步:综合专家意见可得B1，B2，B3，B4方案核的综合结果为:（0.525 1，0.516 7，0.498 8，0.494 1）。

即第一个方案最好。

4 结论

对于专家权重未知、属性权重信息部分已知且决策信息为区间灰数的不确定性多属性决策问题，以灰色系统理论的思想和方法为基础，充分利用区间灰数的核和灰度的信息建立优化模型求属性的权重，在求出属性权重的基础上，运用灰色关联方法分别求取基于核与灰度的关联系数，综合得到专家权重，则可得到方案集的专家意见的综合值，比较各个方案的综合值，比较并排序。基于核和灰度的区间灰数的决策模型充分发挥核与灰度两个方面，简洁合理，考虑了区间灰数的特征，使得决策结果更为科学合理。

［1］JIANG C，HAN X，LIU G R.A nonlinear interval number programming method for uncertain optimization problems［J］. European J of Operational Research，2008，188（1）:1-13.

［2］方志耕，刘思峰，陆芳，等.区间灰数表征与算法改进及其GM（1，1）模型应用研究［J］.中国工程科学，2005，7（2）: 57-61.

［3］XU Z S.Dependent uncertain ordered weighted aggregation operators［J］.Information Fusion，2008，9（2）:310-316.

［4］谢乃明，刘思峰.考虑概率分布的灰数排序方法［J］.系统工程理论与实践，2009，29（4）:169-175.

［5］XU Z S.Dependent uncertain ordered weighted aggregation operators［J］.Information Fusion，2008，9（2）:310-316.

［6］方志耕，刘思峰，陆芳，等.区间灰数表征与算法改进及其GM（1，1）模型应用研究［J］.中国工程科学，2005，7（2）: 57-61.

［7］陈孝新，刘思峰.一种部分权重信息的灰色多属性群决策方法［J］.系统工程与电子技术，2009，31（4）:843—846.

［8］刘思峰，方志耕，谢乃明.基于核和灰度的区间灰数运算法则［J］.系统工程与电子技术，2010，32（2）:313-316.

［9］闫书丽，刘思峰，朱建军，等.基于相对核和精确度的灰数排序方法［J］.控制与决策，2014，29（2）:315-319.

Multi-attribute Group Decision Making Model Based on Kernel and Degree of Greyness of Interval Grey Numbers

LI Yan-ling，YIN Xin-li，YANG Jian
（Rocket Force University of Engineering，Xi’an 710025，China）

In view of the multi-objective group decision problem that the attribute values are interval grey numbers and the weights of experts unknown，the attribute weights partially known，the multi-objective decision-making method based on the kernel and the degree of greyness of the interval grey numbers is proposed.Simplified formation of Interval grey Numbers is given based on kernel and degree of greyness.The optimization model based on the kernel and the degree of greyness of the interval grey numbers is set up and the attribute weights can be solved.The schemes are aggregates with attribute weights.To calculate the grey correlation coefficient separately ofthe kernel and the degree of greyness of the interval grey numbers and combine both of them，then the weights of experts can be obtained.Aggregate the expert opinion and compare the scores of schemes，the best scheme can be chosen.Based on this，a kind of Multi-attribute decision making model is put forward.Based on the kernel and the degree of greyness of the interval grey numbers.Finally，a numerical example to verify the feasibility and effectiveness of the method.

interval grey numbers，Multi-attribute group decision making，the kernel，the degree of greyness

C934

A

1002-0640（2017）03-0017-04

2016-01-12

2016-02-14

国家自然科学基金青年基金资助项目（61501471）

李艳玲（1972- ），女，陕西西安人，教授，博士后。研究方向：决策支持。