仿射变换在初等几何教学中的应用

谭建中，呙立丹

（韶关学院 数学与统计学院， 广东 韶关 512005）

仿射变换在初等几何教学中的应用

谭建中，呙立丹

（韶关学院 数学与统计学院， 广东 韶关 512005）

高等几何是高师院校数学教育专业的主干课程之一，通过实例从平行射影和仿射对应图形两个方面，说明属于高等几何内容之一的仿射变换在解决某些中学几何问题中所起到的作用，阐述高等几何与中学几何的联系和高等几何的思想方法对中学几何的教学的指导作用，使得数学教育专业的师范生能够更好地理解高等几何在实际教学中的应用。

仿射变换；平行射影；高等几何；初等几何；教学

高等几何是高等师范院校数学教育专业的主干课程之一，该专业的学生毕业后，大部分的同学将从事中学数学的教育工作。他们常常对学习高等几何的内容与他们以后从事的中学数学教育有什么关系，即高等几何的学习对他们以后的数学教学会起到什么样的作用而感到困惑。实际上，中学数学教学中与高等几何联系最紧密的是中学几何，或称初等几何。初等几何是高等几何的基础，而高等几何则是初等几何的延伸和拓展。我们可用高等几何的一些原理、方法来分析初等几何的有关问题，使得高等几何能“用高于下”，以便深入理解高等几何对初等几何的指导意义。为此，本文将通过实例说明属于高等几何内容之一的仿射变换在解决初等几何问题中的一些应用。

一、利用平行射影证明几何题

平行射影是最简单的仿射变换，利用两条直线之间的平行射影，将图形中不共线的点和线段投射成共线的点和线段，再利用仿射不变性证明几何题。［1］

例1 设线段AB的中点为M，从AB上另一点C向直线AB的一侧引线段CD，令CD的中点为N， BD的中点为P，MN的中点为Q。求证：直线PQ平分线段AC。［2］

证 如图（1），以DA为射影方向，将点D、N、P平行射影到直线AB上。设D→A，N→E，P→M，根据仿射不变性，因N是DC的中点，所以E是AC的中点。又因P是BD 的中点，所以M是AB的中点，故NE∥PM∥DA，且NE＝PM＝DA，即四边形NPME为平行四边形，因Q是MN的中点，所以三点P、Q、E共线，故直线PQ平分线段AC。

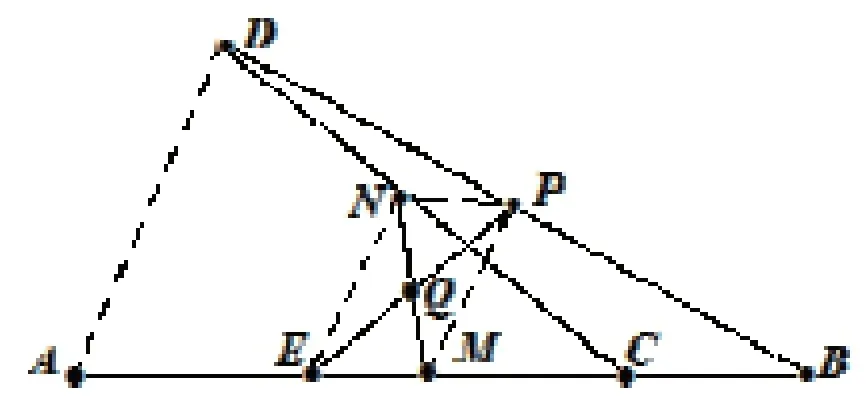
(1)

例2 在ΔABC中，AC＝3AB，自C作LA的平分线的垂线，垂足为D，求证：BC平分AD。

证 如图(2)，设AD交BC于M，以BA 为射影方向，将点M、D平行射影到直线AC上。［2］

设M→E，D→F。 由仿射不变性有AB∥EM∥FD，所以，，故AE＝EM；因为 AC＝3AB，所以，EC＝3EM＝3AE，即：

又因为，∠FDC和∠FCD为等角的余角，所以，∠FDC＝∠FCD，故FC＝DF＝AF，即：

由式(1)和式(2)得：2AF＝4AE，AF＝2AE，E为AF的中点。所以，M为AD的中点，即BC平分AD。

例3 设直线MN过ΔABC的重心G，分别交AB、AC于M、N，求证：。［3］

证 如图(3)，以NM为射影方向作平行射影，将点N、C、D射影到直线AB上。

设 N→M，C→C，D→D。

因为D是BC的中点，所以，由仿射不变性得，D是B C的中点。

又因为G是ΔABC的重心，

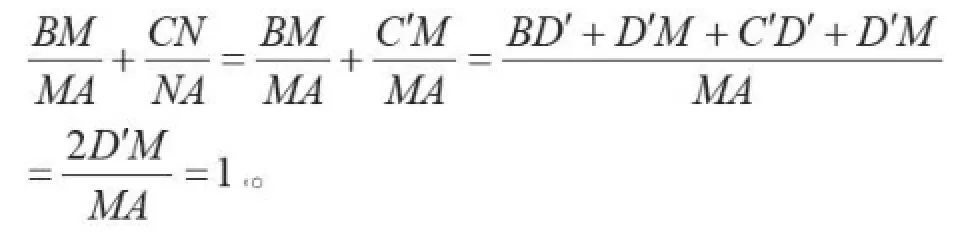
从上面的实例可以看出，平行射影适用于证明有关两平行线段的比或同一直线上两线段的比（特殊情形是线段的中点）的几何命题或可以转化为上述情形的有关命题。如果将上面的证法看成是中学几何中通过添加辅助线来求证的，那么从平行射影的思路即可看出上面例题中的辅助线是怎样做出来的，这就是高等几何对中学几何解题思路方法的启迪或指导。

二、利用仿射对应图形证明几何题

由仿射几何可知，椭圆的特殊仿射像是圆，只要涉及仿射不变性和仿射不变量，且与椭圆有关的命题，都可以通过仿射变换转化为与圆有关的命题，这使得命题的证明过程比较简单。

例4 自椭圆外一点P引椭圆的两条切线，切点分别为A、B，O为椭圆的中心，AO与椭圆交于另一点C，证明：BC∥PO。［3］

证 设仿射变换T将图(4)中的椭圆仿射成图(4')中的圆。图(4')中表示点的字母仍沿用图(4)中对应点相同的字母。根据仿射不变性，在图(4')中，PA、PB为圆O的切线，切点为A、B，由初等几何知识可知：

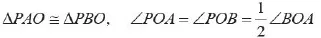
例5 自椭圆外一点A引切线，切点为B，过AB的中点M作割线交椭圆于C、D，连结AC、AD交椭圆于E、F。 求证：AB∥EF。［2］

证 设仿射变换T将图(5)中的椭圆仿射成图(5')中的圆，图(5')中表示点的字母仍沿用图(5)中对应点相同的字母。由仿射不变性，在图(5')中，AB为圆的切线，B为切点，M仍是AB的中点，由割线定理可知：，即，且。所以，△MCA ~ △MAD，∠MAC＝∠MDA。因为 ∠MDA＝∠CEF，所以 ∠BAE＝∠MAC＝∠MDA＝∠CEF＝∠AEF。故AB∥EF。由仿射不变性可知，对图(5)中的椭圆也有AB∥EF。

例6 证明：椭圆的任何一对共轭直径为邻边的平行四边形的面积为定值。

证 椭圆的方程为：

在仿射变换下，椭圆①的一对共轭直径变成圆②的一对互相垂直的直径。设椭圆的一对共轭直径

［1］朱德祥.高等几何［M］.北京：高等教育出版社，1984:152-153.

［2］王林全.初等几何研究教程［M］.广州：暨南大学出版社，1996:17-21.

［3］吕世虎.从高等数学看中学数学［M］.北京：科学出版社,1995:79-81.为邻边的平行四边形的面积为S1，圆的一对互相垂直的直径为邻边的平行四边形的面积为S2，椭圆的面积为S3，圆的面积为S4。

故椭圆①式的任何一对共轭直径为邻边的平行四边形的面积为定值。

三、结语

高等几何涉及到的许多平行射影、仿射不变性和二次曲线的射影性质等内容，都可以对初等几何教学中碰到的一些困难问题给予相应的解析。因此，学习高等几何不仅可以提高在校大学生理解问题与解决问题的能力，还可使中学教师的初等几何教学思路更加开阔，在逻辑思维与三维空间分析能力上会有明显的提升，并且有助于中学生加深对初等几何的理解。

The Applications of Affine Transformation in Elementary Geometry Teaching

TAN Jian-zhong，GUO Li-dan
(College of Mathematics and Statistics, Shaoguan University, Shaoguan 512005, Guangdong, China)

Higher geometry is one of the main courses in the mathematics education major of the normal university. What is the link between the higher geometry and middle school geometry? How does the thinking method of the higher geometry guide the teaching of the middle school geometry? With the examples of parallel projection and affine correspondence graph, we give the facts of solving some questions in middle school geometry with the affine transformations in higher geometry. Finally, we wish that the students majoring mathematics education can understand the application in teaching and learning of higher geometry.

affine transformation; parallel projection; higher geometry; elementary geometry; teaching

G642.1

A

1007-5348（2017）02-0106-03

（责任编辑：邵晓军）

2017-02-01

韶关学院教育教学改革研究项目“突出数学思想方法渗透的《高等数学》教学研究与实践”（SYJY20141545）

谭建中（1958-），男，广东珠海人，韶关学院数学与统计学院副教授；研究方向：数学教育。