新问题新情境新视角
——2017年北京市海淀区七年级(上)期末测试特色试题赏析
☉北京中关村中学 杨爱青
新问题新情境新视角
——2017年北京市海淀区七年级(上)期末测试特色试题赏析
☉北京中关村中学 杨爱青
前不久刚刚结束的海淀区七年级(上)期末统一测试中,有不少优秀的原创题,特别是其中的第23、26、27题,通过给基础习题添加“新问题”,给基本模型创设“新情境”,给核心概念赋予“新视角”,为考生提供了一个发挥其创造能力的平台.笔者把对考题的深入思考和解读整理成文,与同行探讨交流.
一、给基础习题添加“新问题”
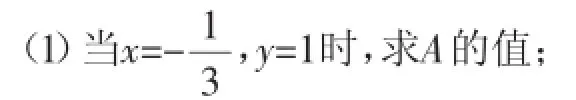
(2)若使求得的A的值与(1)中的结果相同,则给出的x、y的条件还可以是________.
赏析:把学生熟悉的常规问题作为第(1)问,在此基础上增加了第(2)问,一个开放性的问题.对于第(2)问,由于代数式A的化简结果为-6x+2y,因此,给出的x、y的条件可以是与题目(1)中不同的x、y的具体值,也可以直接给出x和y之间的关系-6x+2y=4或其等价形式.找与题目(1)中不同的x、y的具体值,可以先给出x(y)的一个具体值,然后代入-6x+2y=4,把问题转化为一元一次方程去求解.
第(2)问的开放性问题还可以如下设计:
这样的设计可以帮助学生体会代数式求值的本质含义,领悟代数式的结构对其求值的影响,并通过对问题的解答,培养学生的发散性思维和创新意识.
二、给基本模型创设“新情境”
考题2:(第26题)如图1,由于保管不善,长为40米的拔河比赛专用绳AB左右两端各有一段(AC和BD)磨损了,磨损后的麻绳不再符合比赛要求.
已知磨损的麻绳总长度不足20米.只利用麻绳AB和一把剪刀(剪刀只用于剪断麻绳)就可以得到一条长20米的拔河比赛专用绳EF.
请你按照要求完成下列任务:
(1)在图1中标出点E、F的位置,并对如何确定点E、F作出简要说明;
(2)说明(1)中所标EF符合要求.

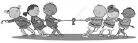
图1
赏析:这道题以真实情景“拔河比赛用绳”为背景,贴近学生生活实际,图文并茂符合初一学生的年龄特点.题目模型明确,难度适当,在立足基础的同时,着力内容创新,考生只有具备了相应的思维方法,才能应对本题的新情境、新变化.图2中的模型是本题考查的重点,它广泛地蕴含在教材的例、习题之中,因此本题给学生以亲切感,题目的解题思路和方法在学生的学习过程中都有“本”可循.

图2
试题入口较宽,思路多,不同能力层次的学生可以寻求到不同的解题思路.
对于第(1)问,首先,要找的“线段EF”需满足两个条件,一个是长度为AB的一半,另一个是无磨损,也就是说点E、F都要在线段CD上,其次,找“线段EF”的工具有限制,只能用麻绳AB和剪刀(剪刀只能用于剪断麻绳).用叠合法找AB的中点可以得到AB的一半,这一点学生非常熟悉,而怎么做到EF既是AB的一半又要点E、F在线段CD上呢?这时仅仅能熟练地做出见过的题目和题型就不够了,要能灵活地运用所学知识将其化归为熟悉的问题来解决.这里解决问题的一个策略就是“两个条件”一个一个地来,一般情况下我们先从容易的那个入手,按照这样的思路解题有两类方法,一类是“先剪拼再用叠合法找中点”,另一类是“先用叠合法找中点再剪拼”,具体的解法见方法1、方法2和方法3.
方法1:如图3,剪下AC拼在AB的延长线上,使点A与点B重合,点C的落点为C′,对折得线段CC′的中点F,点E与点C重合.
方法2:如图4,沿点C折叠,点A的落点为A′,剪下BD拼在AA′的延长线上,使点D与点A′重合,点B的落点为B′,再对折得线段B′D的中点F,点E与点C重合.
方法3:如图5,对折得线段AB的中点M,剪下AC拼在AM的延长线上,使点A与点M重合,点C的落点为F,点E与点C重合.
方法1、方法2、方法3是“一个线段中点模型”的应用,相对来讲更容易些,从阅卷反馈来看也是绝大多数学生的做法.
除了上面的三种方法,还可以应用“两个中点模型”来解决问题,具体的解法见方法4、方法5.
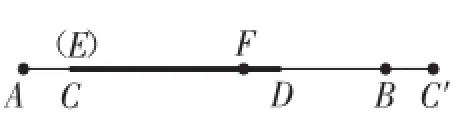
图3

图4
方法4:如图6,沿点C折叠,点A的落点为M,对折得线段BM的中点F,点E与点C重合.
方法5:如图7,沿点C折叠,点A的落点为A′,沿点D折叠,点B的落点为B′,M为线段A′B′上任意一点,对折得线段AM的中点E,对折得线段BM的中点F(方法4是点M与点A′重合时的特殊情况).
方法1至方法4相对来说操作简单,更接近学生现阶段的思维水平,而方法5相对前面4种方法更具一般性.
针对第(1)问不同的“操作方法”,第(2)问都有相应的证明方法与之对应,这里就不一一赘述了.

图6

图7
三、给核心概念赋予“新视角”
考题3:(第27题)在数轴上,把表示数1的点称为基准点,记作点.对于两个不同的点M和N,若点M、点N到点的距离相等,则称点M与点N互为基准变换点.例如:图8中,点M表示数-1,点N表示数3,它们与基准点的距离都是2个单位长度,点M与点N互为基准变换点.

图8
(1)已知点A表示数a,点B表示数b,点A与点B互为基准变换点.
①若a=0,则b=_______;若a=4,则b=_______;
②用含a的式子表示b,则b=_______.
(3)点P在点Q的左边,点P与点Q之间的距离为8个单位长度.对P、Q两点作如下操作:点P沿数轴向右移动k(k>0)个单位长度得到P1,P2为P1的基准变换点,点P2沿数轴向右移动k个单位长度得到P3,P4为P3的基准变换点,……,依此顺序不断地重复,得到P5、P6、…、Pn.Q1为Q的基准变换点,将数轴沿原点对折后Q1的落点为Q2,Q3为Q2的基准变换点,将数轴沿原点对折后Q3的落点为Q4,……,依此顺序不断地重复,得到Q5、Q6、…、Qn.若无论k为何值,Pn与Qn两点间的距离都是4,则n=_________.
赏析:这道题为整卷的最后一题,在此题的解决过程中体现了浓厚的数形结合思想.试题着眼于学生已有的“绝对值、相反数及线段和线段中点”的经验,让学生经历认识基准变换点,探求互为基准变换点的两个点的坐标规律,解决简单问题,解决综合问题的过程,并通过这样的过程,让学生在潜移默化中种下数形结合的种子.
试题的三个问题逐层深入,前一个问题是后一个问题的铺垫,第(1)问是引导学生阅读,帮助学生理解“基准变换点”,为第(2)问、第(3)问利用“基准变换点”解决问题作必要的准备.第(1)问、第(2)问比较简单,这里就不再赘述了.第(3)问,一方面可以由前面得到的互为基准变换点的两个点的坐标规律“和为2”,从“数”的角度找寻P、Q两点的变换规律;另一方面,由“基准变换点”的概念可知:基准点为连接互为基准变换点的两点所得线段的中点,因此还可以从“形”的角度找寻P、Q两点的变换规律,其解决问题的思维过程大致如下.
思路1:设P点表示的数为p,则Q点表示的数为p+8.

由于无论k为何值,Pn与Qn两点间的距离都是4,因此有:
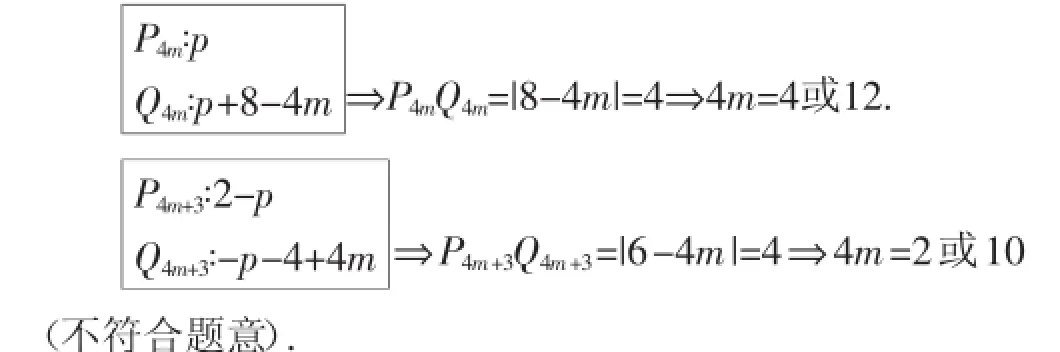
所以n=4或12.
思路2:
P点:
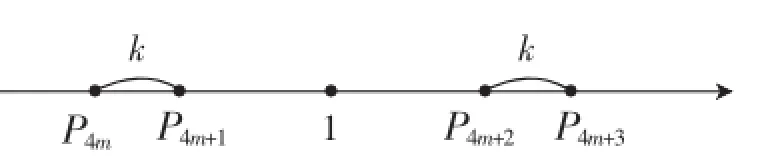
图9
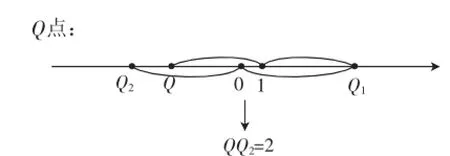
图10
同理:

图11
由于无论k为何值,Pn与Qn两点间的距离都是4,因此有:
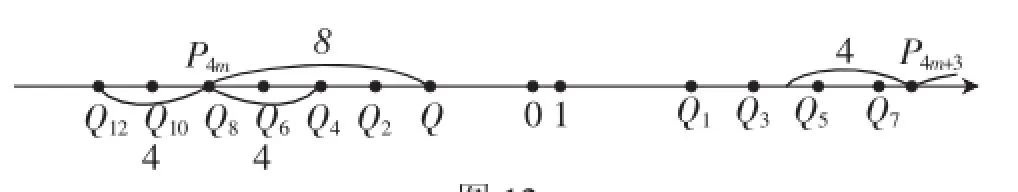
图12
所以n=4或12.
从上面的思维过程可以看出,第(3)问的解决要依赖于学生对问题的数学本质的理解,靠记住一些结论、生搬硬套显然是行不通的.
题目的一些拓展延伸:
在数轴上,点A表示数a,点B表示数b,点A与点B不重合.
(1)若a、b互为相反数,则a+b=0;
(2)若A、B两点互为基准变换点,则a+b=2;
……
(3)若A、B两点到点C(表示数c)的距离相等,则a+ b=2c.
实际上,这里的(1)、(2)是数轴上中点坐标公式的特殊情况,后面还可以把这里的中点坐标公式进行推广,从而得到平面上的线段中点的坐标公式.
四、一点感悟
给基础习题添加“新问题”,给基本模型创设“新情境”,给核心概念赋予“新视角”,这样的试题,一方面它们源于教材,其解题思路和方法在学生的学习过程中有“本”可循;另一方面,它们又打破了命题的模式,在考查基础的同时,较好地考查学生的开放性思维、问题解决能力和创新能力,符合当前考试改革“新”“宽”“活”的趋势和要求,对我们的教学有着积极的导向.

