基于学生思维水平的评价标准制定*
——以一个“分割”任务的评价标准发展过程为例
☉北京师范大学未来教育高精尖创新中心 曹辰☉北京师范大学教育学部何声清
基于学生思维水平的评价标准制定*
——以一个“分割”任务的评价标准发展过程为例
☉北京师范大学未来教育高精尖创新中心 曹辰
☉北京师范大学教育学部何声清
无论是终结性的学业测试还是过程性的课堂随考,对学生的学习表现进行科学评价一直是数学测评的基本内容和目标.传统的评价标准往往过于简单,客观题一般是“正确”“错误”的二元判分;主观题一般是按照“解题过程”分步判分.不可否认的是,这种形式的评价标准对学生“成绩”的判定有其合理性,也比较高效.然而,它难以深及学生的数学思维水平,因而也难以揭示学生作答的深层原因.本文以一个“分割”任务为例,通过“直观化—层次化—数学化”的探索过程,逐步明确学生作答的思维水平及深化问题的评价标准.
一、数学任务呈现
如图1所示的点阵摆放方式是每行n个,共n行,称作“n×n点阵”.小明、小贝、小梦对该点阵进行了不同的分割,将各区域的点数累加起来,发现了一些有趣的结论.

图1
小明按照方式1进行分割,将点阵分成n个区域.第1个区域有n个点,第2个区域有n个点,第3个区域有n个点,…,第n个区域有n个点.所以,该点阵中点的总数为“点阵的每一个区域中点的个数之和”,用数学表达式记为
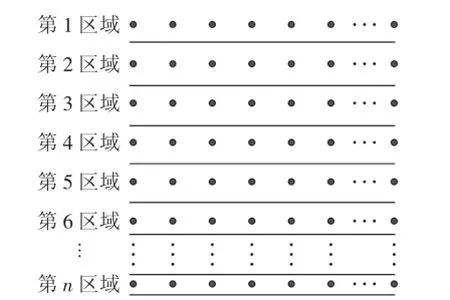
图2:方式1
小贝按照方式2进行分割,将点阵分成n个区域.第1个区域有1个点,第2个区域有3个点,第3个区域有5个点,…,第n个区域有2n-1个点.所以,该点阵中点的总数为“点阵的所有区域中点的个数之和”,用数学表达式记为:1+3+5+…+(2n-1)=n2.
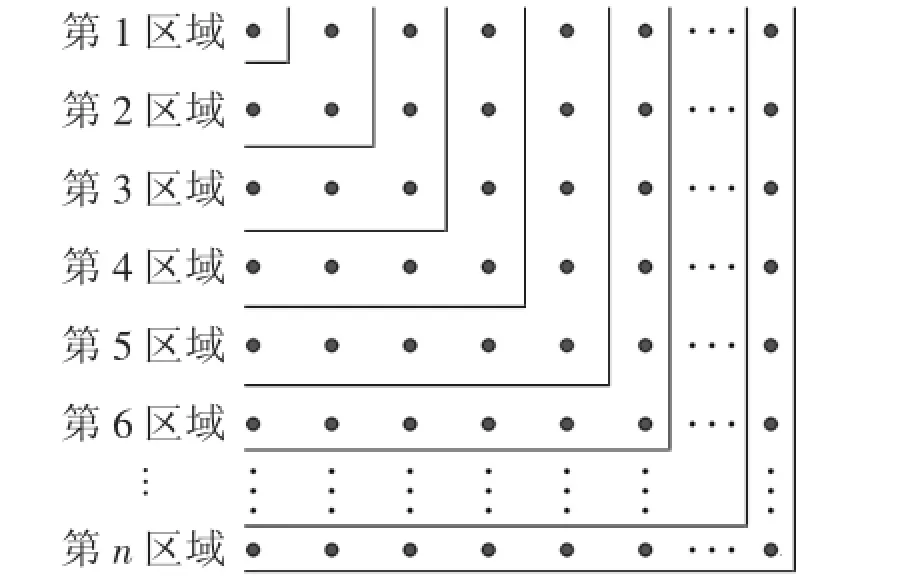
图3:方式2
小梦按照方式3进行分割,将点阵划分为2个区域.第1个区域有(n-1)×(n-1)个点,第2个区域有n+n-1(即2n-1)个点.所以,该点阵中点的总数为“点阵的所有区域中点的个数之和”,用数学表达式记为:(n-1)2+2n-1=n2.
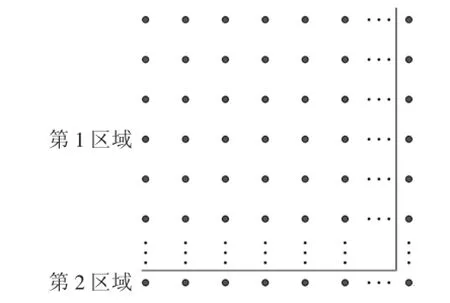
图4:方式3
你还有新的分割方式吗?请作出你的分割,并写出你从该分割方式中发现的等式.
在对该开放性问题进行评价的过程中,我们遇到了困惑:学生对图形的分割各式各样,相应的表达式也五花八门.如何针对学生的作答,制定出一个既能反映学生的思维水平,又能兼顾作答准确性的评分标准呢?在实际操作中,我们进行了以下探索.
二、“直观化”:评价标准的初步划分及其局限
我们首先根据分割线条的几何形状对其进行了直观的初步划分.在小明、小贝及小梦的范例中,对n×n点阵的分割出现了横线型、折线型两种情形.在学生的作答中,大致出现了以下4种分割方式(如图5~8):横(竖)线型、折线型、斜线型、方块型.

图5:横线型
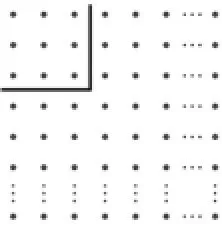
图6:折线型
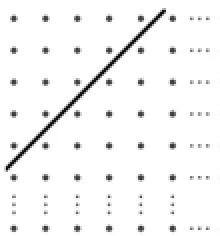
图7:斜线型
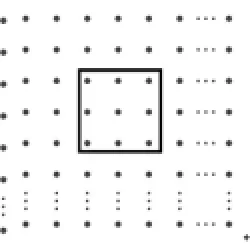
图8:方块型
如何根据学生的作答来判定其思维水平呢?我们认为,在之前的范例中已经出现过横线型和折线型分割,这给学生提供了基本参照和模仿的可能;而斜线型及方块型分割没有出现过.据此,我们对学生的思维水平进行了初步判断:斜线型、方块型分割的思维水平高于折线型、横(竖)线型分割的思维水平.但如何在折线型与横(竖)线型之间,斜线型与方块型之间进行比较呢?参照学生在最后的等式表达式中的作答,我们认为,折线型分割的等式表达形式比横(竖)线型分割的等式表达形式复杂,因此折线型分割的思维水平比横(竖)线型分割的要高;同理,斜线型分割的思维水平高于方块型分割的.综上所述,我们认为4种分割方式的水平排序为斜线型>方块型>折线型>横(竖)线型.
然而我们又发现,即使在同类别的几何形状分割中,学生的水平也会有一定的区别.以竖线型分割为例(如图9~10),有的学生只画了一道竖线,将点阵分割为两个区域;而有的学生则将点阵分割为n个区域.

图9:有限的竖线型分割

图10:无限的竖线型分割
我们认为,将点阵分割为无限个区域的学生的思维水平高于将点阵分割为有限个区域的学生的思维水平.据此,在根据学生分割的几何形状进行分类后,我们在每个大类中又根据分割区域的个数,将其进一步细分为有限型和无限型两类.总计为4大类8小类(如表1),基本涵盖了学生的全部作答情况.
在对上述4大类8小类分割的赋值过程中,我们又面临了新的问题:如何针对这8小类的作答,更加具体地区分出学生思维层次的高低?在之前的讨论中,我们仅仅在这4大类之间进行了水平排序,但一旦加入“分割区域的有限或无限性”变量,新的8小类水平的排序似乎不那么容易.例如,对于斜线型中的有限区域分割和横线型中的无限区域分割,哪一个更能体现学生的思维深度呢?并且,即使我们将这8小类进行了最终排序,但在评分过程中因为分类过细而难以操作.因此,上述评分标准仍需调整.
三、“层次化”:评分标准的进一步探索
若仅仅根据几何特征对学生的分割进行分类,则难以深及问题实质.为此,我们试图对上述分割的深层原因进行分析.在范例中,我们已经呈现了横线型及折线型的分割,如果学生在最后的开放性问题中采用了横(竖)型、折线型的分割,我们认为其是在范例的基础之上进行了修改,基本属于模仿的思维水平.对于斜线型分割,虽然范例中没有出现过,但在几何形状上也属于直线型,因此我们认为,作出斜线型分割的学生是在范例的基础上进行了较大程度的改动,体现了对于范例的迁移理解能力.对于方块型分割,无论是其几何特征,还是最后的等式表达式,均是范例中没有出现过的,我们认为这种分割已经超出了模仿、迁移的范畴,达到了创新的层次,体现了较高的思维水平.综上所述,我们将学生的分割水平排序调整为:方块型>斜线型>横(竖)线型、折线型.
上述水平划分标准虽然对4大类分割排序进行了简化,但之前的问题还是没有得到较好解决:对于同一类几何形状的分割,我们该如何体现其区别?进一步,我们将研究的重心放到了最后的等式表达式上.例如,以下两个折线型分割方式中(如图11~12),虽然都是将点阵分割为两个区域,但体现的思维水平是相同的吗?

图11:“有限+无限”折线型分割

图12:“无限+无限”折线型分割
总体而言,上述分割可归结为“有限+无限”型与“无限+无限”型两类.从表达式来看,前者一般是“数字+含n的表达式”,后者一般是“含k的表达式+含n的表达式”.因此在后续的分析中,我们尝试脱离分割方式的几何特征,仅从分割区域的数量上进行排序.即:分割的区域越多,越能体现学生思维水平的层次.但问题也随之出现:在分割区域数量相同的情况下,如何评估不同的分割方式所体现的思维水平呢?若简单地认为“无限”优于“有限”,仅仅比较无限区域的个数的话,就会出现以下情况(如图13~14).图13的分割是4个“无限”区域的累加,其表达式为:n+2n+3n+(n-6)n=n2;图14的分割是1个“有限”区域和3个“无限”区域的累加,其表达式为:16+(n-4)×4+(n-4)×4+(n-4)2=n2.尽管前者有较多的“无限”区域,然而其表达式相对简单.

图13:“无限+无限+无限+无限”型

图14“有限+无限+无限+无限”型
综上所述,无论是从“模仿、迁移或创新”的角度进行排序,还是从分割区域的个数进行排序,均不具有可行性与合理性.尽管如此,这些尝试为我们后续探索打开了思路:我们应该脱离分割方式的几何形状表象,基于其背后的深层思维表现评估学生的水平.
四、“数学化”:评分标准的深化及其合理性
在探索该开放性问题的评分标准时,我们对小明、小贝及小梦的分割方式进行了反思,并有了意外的发现.
1.方式1的分割可以归结为“二次函数型”.例如,小明采用横线型分割将点阵分为n个区域,所得的表达式为“n个n相加”(即n2).在我们的测试中,也出现了类似的情况.例如,有学生进行了如下分割(如图15),其表达式为:3n+(n-3)n=n2.更一般地,该类分割可以归纳为:kn+(n-k)n=n2.

图15
2.方式2的分割可以归结为“等差结构型”.例如,小贝的分割虽然也将点阵分成了n个区域,但它更体现了其对于“规律”的探索,从而采用“等差数列的前n项和”的表达方式.更一般地,该类分割还有以下几种常见形式(如图16~17).

图16:“1+2+3…”型(部分)

图17:“1+5+9…”型(部分)
3.方式3的分割可以归结为“完全平方公式型”.例如,小梦的分割可以看作是将点阵分为4个区域(如图18),其表达式为:(n-1)2+2(n-1)+1=n2,这是一个完全平方公式的结构.更一般地,该点阵可以作如下分割(如图19),其表达式为:k2+2(n-k)·k+(n-k)2=n2.

图18:“完全平方公式型”示例

图19:“完全平方公式型”一般形式
4.“方块型”分割可以归结为“平方差公式型”.例如,对于图20的分割,其表达式为:42+(n-4)·n+4·(n-4)=n2.若对其稍加变换,它是一个典型的“平方差”结构:n2-42=(n-4)·n+4·(n-4)=(n+4)(n-4).更一般地,该类分割的一般形式如图21所示,其表达式为:k2+(n-k)·n+k(n-k)=n2.

图20:“平方差公式型”示例

图21:“平方差公式型”的一般形式
实际上,“平方差公式型”和“完全平方公式型”可以从一般意义上视为一类情形.例如,如果将图20的分割改为图22的“等价形式”,我们发现它还可以用“完全平方公式型”表达.尽管如此,我们认为有必要对其进行区分.

图22:“平方差公式型”的等价形式
综上,我们对学生作答的评价标准完全脱离了其几何形状的直观特征和尚不够明朗的层次性划分,转而从“数学化”的视角对其进行了更深层次的剖析,厘清了几类典型的思维表现.
五、反思
本文对学生在“分割”任务中的评分标准是在“直观化—层次化—数学化”的过程中逐步清晰和深化的.我们深刻体会到,关于学生学习的评价,只有深入其思维实质,才真正对我们了解学生有实际的意义.诚然,当前的评价标准尚不足以概括学生的全部作答,但这样的划分为我们的后续改进提供了基本视角.
实际上,我们在设置该开放题时并未对其评价标准做过多预设,该文的评价标准基本上是逐渐探索而生成的.诚然,在制定学生作答表现的评价标准方面,一个基本的经验是:基于学生作答作合理分类和概括.但我们仍需指出,教师在设置评价任务时,有必要对任务本身进行必要的设计和预设.换言之,我们要考查学生哪方面的表现?设置什么问题去考查?如何通过该问题去考查?这都需要教师在教学中多下功夫.
本文系北京师范大学未来教育高精尖创新中心项目“中学数学学科诊断分析工具开发与应用研究”(项目编号:BJAICFE2016SR-008)的阶段性成果.

