基于标准，关注本质，考查素养：例析二次函数压轴题的命制*

☉江苏扬州市初中数学 张晓林名师工作室 石树伟

基于标准，关注本质，考查素养：例析二次函数压轴题的命制*

☉江苏扬州市初中数学 张晓林名师工作室 石树伟

中考压轴题的高区分度及由其衍生的高利害性，决定了压轴题对一线教学具有较强的导向作用.二次函数是初中数学的核心内容，无论是知识的综合性还是思维的层次性，都当之无愧地占据着初中代数的“制高点”.因此，二次函数是肩负区分功能的中考压轴题的命题热点，二次函数压轴题的命制需正本清源，以利于正确引领一线的教学.

一、从一道中考题分析二次函数压轴题的命题误区

当前，许多地方二次函数压轴题的命制存在着一定的误区，命题方向偏离了课程标准要求和函数概念本质.下面先从一道常见的二次函数中考压轴题说起.

例1如图1，二次函数y=ax2+bx的图像过点A（-1，3），顶点B的横坐标为1.

（1）求这个二次函数的表达式.

（2）点P在该二次函数的图像上，点Q在x轴上，若以A、B、P、Q为顶点的四边形是平行四边形，求点P的坐标.

（3）如图2，一次函数y=kx（k>0）的图像与该二次函数的图像交于O、C两点，点T为该二次函数图像上位于直线OC下方的动点，过点T作直线TM⊥OC，垂足为点M，且M在线段OC上（不与O、C重合），过点T作直线TN∥y轴交OC于点N.若在点T运动的过程中，为常数，试确定k的值.

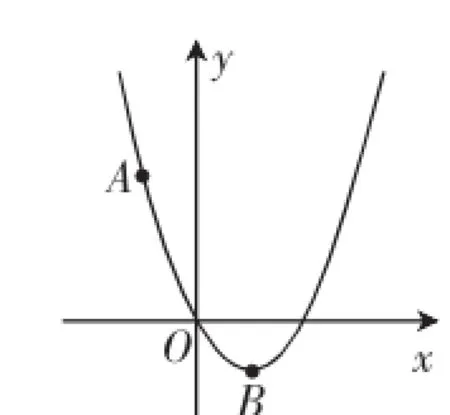
图1

图2

1.解题思路分析.

对于第（1）题，利用待定系数法易得这个二次函数的表达式为y=x2-2x.

第（2）题需分类讨论：①当AB为平行四边形一边时，易得点P的纵坐标为4；②当AB为平行四边形的对角线时，易得点P的纵坐标为2.因为点P在该二次函数的图像上，易得点P的坐标为

对于第（3）题，设点T（n，n2-2n），则点N（n，kn），TN= kn-（n2-2n）.由勾股定理易得由△TMN∽△ODN，可得MN=则，上式为不随n变化的常数，则1-2k=0，即此时

2.命题误区分析.

本题是一道二次函数综合题，辅之以平行四边形性质和三角形相似的应用，渗透考查数形结合、分类讨论等重要数学思想，具有较强的综合性.在点T运动的过程中为常数，说明该比值与点T的坐标（横坐标）无关，从而可得该比值化简后与横坐标（未知数）相关的系数为0，由此确定k的值，这里除了要求学生深刻领会问题的本质，还需学生具备较强的代数运算定向变形的能力，充分考查学生思维的深刻性和运算能力，具有较强的区分度.通过阅卷情况看，本题很好地发挥了把关区分功能，有效达成了命题意图.

从解题过程看，第（1）题重点考查利用待定系数法求二次函数的表达式，而第（2）（3）题则主要是平行四边形、相似三角形等知识和分类讨论、数形结合等思想的应用，几何知识的应用成为问题突破的关键，二次函数仅在解题开始或结束时借表达式来设或求点的坐标.从以上分析可以看出，二次函数其实不是本题考查的重点，第（1）题仅为第（2）（3）题准备一个二次函数的背景和铺垫.

以二次函数为背景，将二次函数与三角形、四边形、圆等知识结合起来考查学生的综合应用能力，这是现在流行的二次函数压轴题的命题方式，但这样考查有两方面的弊端：一是掐头去尾烧中段，“过度解析化”地考查二次函数，对二次函数的来源和应用关注不够，偏离二次函数内容的课标要求；二是“人为拼凑”的痕迹严重，过于注重二次函数具体静态细节和解题技巧的考查，偏离函数概念的本质，总体上对数学核心素养的考查缺失.

二、课标要求概念本质导向核心素养考查

1.课标要求对二次函数命题的启示.

二次函数从属于函数，因此先来看一下《义务教育数学课程标准（2011年版）》（本文简称课标或标准）中“课程内容”部分对“函数”内容的要求：

（1）探索简单实例中的数量关系和变化规律，了解常量、变量的意义.

（2）结合实例，了解函数的概念和三种表示法，能举出函数的实例.

（3）能结合图像对简单实际问题中的函数关系进行分析.

（4）能确定简单实际问题中函数自变量的取值范围，并会求出函数值.

（5）能用适当的函数表示法刻画简单实际问题中变量之间的关系.

（6）结合对函数关系的分析，能对变量的变化情况进行初步讨论.

课标中“课程内容”部分对“二次函数”内容的要求如下：

（1）通过对实际问题的分析，体会二次函数的意义.

（2）会用描点法画出二次函数的图像，通过图像了解二次函数的性质.

（3）会用配方法将数字系数的二次函数的表达式化为y=a（x-h）2+k的形式，并能由此得到二次函数图像的顶点坐标，说出图像的开口方向，画出图像的对称轴，并能解决简单实际问题.

（4）会利用二次函数的图像求一元二次方程的近似解.

（5）知道给定不共线三点的坐标可以确定一个二次函数.

从以上函数和二次函数内容的课标要求可以看出，二次函数的学习需联系实际，学习结果指向解决实际问题，即学习二次函数的概念、表示、图像、性质的目的是解决简单实际问题.当然，这里的实际问题可以是生活现实中的实际问题，也可以是数学现实中的实际问题.基于标准的二次函数试题命制应重视联系实际的函数应用意识和能力的考查.

2.概念本质对二次函数命题的启示.

初中阶段的函数概念是动态的、宏观的变量说，它是从大局着眼考察总体发展趋势，观察变量之间彼此的依存关系，其本质是运动变化过程中变量之间的依赖关系.高中阶段的函数概念则是静态的、微观的对应说，它是从局部着眼深入精细考察每一个细节，强调具体的对应关系，其本质是两个集合元素之间精确化的对应关系.变量说与对应说各有优劣，没有好坏高下之分，但教学和考查的要求应切合学生的年龄特征和学习阶段.

真正的实际问题不会告诉学生“这个问题里面有函数关系”或“这个问题要用××函数去解决”，学生遇到实际问题时首先要能自主发现实际问题中变量之间的依赖关系，主动构造函数去解决问题.因此，函数（包括二次函数）的学习和考查应关注函数概念本质，初中阶段关注本质的二次函数试题命制应以运动变化过程中变量之间函数关系的自主发现、构造和应用为主.

3.基于标准关注本质促进数学核心素养考查.

课标要求和概念本质启示二次函数的考查应重视联系实际的函数应用意识和能力的考查，在函数关系的自主发现过程中考查学生的数学抽象素养，在函数关系的自主构造和应用中考查学生的数学建模素养，从而引领、促进数学核心素养在平时教学中落地生根.

三、基于标准关注本质考查素养的二次函数压轴题例析

近年来，基于标准关注本质的二次函数试题不断出现，对二次函数的考查开始回归自然、回归函数的本质，重视对函数建模思想和二次函数对称性、增减性及最值等主要性质实际应用的考查，较好地体现了“问题情境—建立模型—解释、应用与拓展”这一知识形成与应用的过程，对一线教学起到了正确的导向作用.但总体上这类试题占比还偏小，有的试题在贴近标准关注本质考查素养方面还有待提升.下面举两例分析.

1.数学现实中的二次函数应用压轴题举例.

例2（2013·江苏扬州）如图3，在梯形ABCD中，AB∥CD，∠B=90°，AB=2，CD=1，BC=m，P为线段BC上一动点，且和B、C不重合，连接PA，过P作PE⊥PA交CD所在直线于E.设BP=x，CE=y.

（1）求y与x的函数关系式；

（2）若点P在线段BC上运动时，点E总在线段CD上，求m的取值范围；

（3）如图4，若m=4，将△PEC沿PE翻折至△PEG的位置，∠BAG=90°，求BP的长.

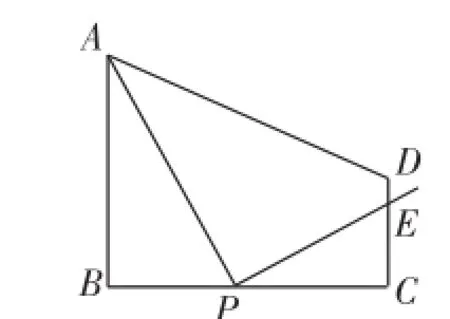
图3

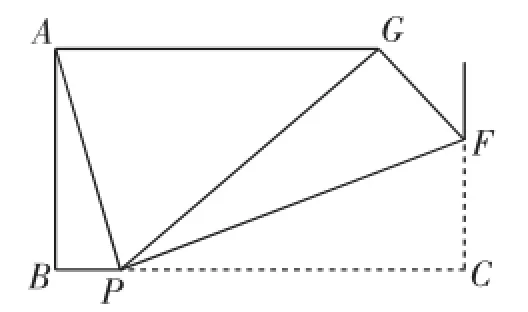
图4

【命题分析】本题看起来是一道动态几何题，但解决问题所用的知识及问题突破的关键主要是二次函数，因此本质上是一道几何背景下的二次函数应用压轴题.第（1）题图形中蕴含有一个三角形相似的基本图形——三垂直模型，由相似三角形的性质容易构造得到答案，第（2）（3）题则应用所得的二次函数解决一些几何问题.第（2）题很好地考查学生对问题本质的认识，“点E总在线段CD上”可以转化为“y总是小于CD的长”，进一步转化为“y的最大值小于CD的长”，从而应用二次函数的最值知识解决问题，对学生转化问题的意识和思维的深刻性要求较高.第（3）题对图形折叠中存在的一些几何性质的考查较为深入，最后将已知量、未知量集中到一个直角三角形中应用勾股定理列方程求解，整题具有一定的综合性.

初看这道题，觉得三问之间层层深入，自然流畅.但细思这道题，则会觉得第（1）题“求y与x的函数关系式”是指令学生构造函数，牵引着学生突破解决问题的关键，而不是学生自己发现运动过程中CE（y）与BP（x）之间存在依赖关系，从而主动构造函数，丧失了考查学生对函数本质理解和主动构造函数解决问题意识的大好机会.

【试题改编】基于以上分析，可对例2进行如下改编：

如图3，在梯形ABCD中，AB∥CD，∠B=90°，AB=2，CD=1，BC=m，P为线段BC上的一动点，且和B、C不重合，连接PA，过P作PE⊥PA交CD所在直线于E.

（1）在图3中找出一对相似三角形，并说明理由；

（2）若点P在线段BC上运动时，点E总在线段CD上，求m的取值范围；

（3）如图4，若m=4，将△PEC沿PE翻折至△PEG的位置，∠BAG=90°，求BP的长.

【改编分析】将第（1）题改为寻找相似三角形并说明理由，目的是体现压轴题“起点低，尾巴翘”的要求，增加试题的“入口宽度”，且不突破本题解决的关键.第（2）题“点E总在线段CD上”即“CE的长总是小于CD的长”，则需将CE的长表示出来.学生若能宏观考察整个运动过程，则容易发现CE的长随着点P位置的变化而变化，且随着点P从B运动到C，CE的长从0逐步增大，达到一个最大值后又逐步缩小至0，发现运动过程中CE与BP之间存在着函数关系，而且估计还是一个二次函数，从而主动设BP的长为自变量，CE的长为因变量（即函数），构造CE与BP之间的函数关系解决问题.这样改编不是指令学生构造指定变量之间的函数关系，而是要求学生主动发现存在依赖关系的两个变量，主动构造两个变量之间的函数关系，有利于考查学生对函数本质的理解和自主构造函数解决问题的意识.

2.生活现实中的二次函数应用压轴题举例.

例3（2015·江苏扬州）科研所计划建一幢宿舍楼，因为科研所实验中会产生辐射，所以需要有两项配套工程：①在科研所到宿舍楼之间修一条路，②对宿舍楼进行防辐射处理.已知防辐射费y万元与科研所到宿舍楼的距离xkm之间的关系式为，当科研所到宿舍楼的距离为1km时，防辐射费用为720万元；当科研所到宿舍楼的距离为9km或大于9km时，辐射影响忽略不计，不进行防辐射处理.设每公里修路的费用为m万元，配套工程费w=防辐射费+修路费.

（1）当科研所到宿舍楼的距离x=9km时，防辐射费y= _______万元，a=_______，b=_______；

（2）若每公里修路的费用为90万元，当科研所到宿舍楼的距离为多少千米时，配套工程费最少？

（3）如果配套工程费不超过675万元，且科研所到宿舍楼的距离小于9km，求每公里修路费用m万元的最大值.

【命题分析】本题是一道生活背景下的二次函数应用压轴题，第（1）题是待定系数法的应用，第（2）（3）题是主动构造二次函数并应用二次函数最值解决实际问题.对于第（2）题，学生容易发现配套工程费与科研所到宿舍楼的距离之间存在着依赖关系，且由“当科研所到宿舍楼的距离为多少千米时，配套工程费最少”容易联想到二次函数“当自变量x=……时，函数y有最大（小）值为……”，从而主动构造函数解决问题，有利于学生数学抽象和函数建模素养的考查.

1.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［S］.北京：北京师范大学出版社，2012.

2.石树伟.问题研究：入乎其内，出乎其外——以一道二次函数题的研究为例［J］.中国数学教育，2011（7/8）.

*本文系江苏省教育科学十三五规划立项课题“农村初中生数学核心素养培养的途径与策略研究”（XC-c/2016/20）及扬州市教育科学十二五规划立项课题“回归本色的数学教育主张理论与实践研究”（G/15/P/027）的成果之一．