中考评价视角下的复习课对话教学——以“圆”的复习课为例

☉江苏江阴市第二中学 蒋敏霞

中考评价视角下的复习课对话教学
——以“圆”的复习课为例

☉江苏江阴市第二中学 蒋敏霞

中考评价的主要载体是试题本身，命题者通过对试题的命制实现中考评价的目的.那么如何有效地进行复习课的教学就成为了中考研究的一个视角.在课堂中，师生是两个矛盾统一的相生体，师生之间的合作与交流往往可以看成是实现课堂有效性的一大途径.现阶段比较流行的是以对话交流为主要途径的教学方式，师生之间通过交流与沟通，不断地产生共鸣，相互促进，共同发展.巴西教育学者保罗·弗莱雷说过：“没有了相互之间的问答，就没有了交流，也就无法实现真正意义的教育”.我国教育学家钟启泉教授指出：“对话”中的不同见解绝不是攻击，而是充实自己的见解，围绕一个共同事物的观点相互补充.真正的“对话”总是不断地臻于柳暗花明的境界.通过以上的“对话”形式，教师向学生传递知识，师生双方共同提升，实现双赢的目的.

中考的初衷是选拔适合下一阶段学习的学生，而教学的本质首先是为了深化学生的理解，加强学生对数学的认识，如果说得功利一些，也不外乎是为了考出一个良好的成绩，而思维对话的方式正是在这样的评价标准体系下应运而生的.新的课程标准指出，教学过程需要师生之间的交流与互动，是一个动态的生成过程.教师的教是为了促进学生更好地学，帮助学生建立有效的模型，而通过互相之间的对话很方便来实施这一过程.本文试图通过笔者教学中的一堂“圆”的复习课的教学，谈一些个人的感悟和体会.

一、情境引入，走出思维困境

问题情境：如图1，有一内部装有水的直圆柱形水桶，桶高20公分；桶中有一个圆柱形的铁柱，铁柱的高度为30公分，将铁柱放置在水桶中，这个时候水面的高度为12公分，水桶与铁柱底面半径的比正好是2∶1.现在小茗同学想把这个铁柱拿到外面来，在这个过程中水量没有变化，那么此时水桶内的水面高度为（）公分.

A.4.5B.6C.8D.9

这样的问题如何解决呢？师生之间的交互性谈话不失为一种非常好的途径，在简单的一问一答中实现双赢.下面是师生之间的对话过程：

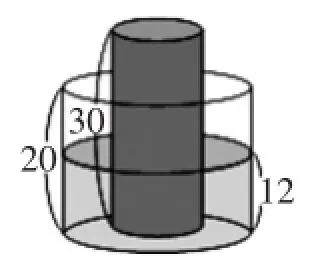
图1

师：如何分析？

生：可以通过比例关系来解决.

师：具体说一说.

生：由题意知：水桶底面半径：铁柱底面半径=2∶1，水桶底面积∶铁柱底面积=22∶12=4∶1，可以设铁柱底面积为a，水桶底面积为4a，则水桶底面扣除铁柱部分的环形区域面积为4a-a=3a，原有的水量为3a×12=36a.

师：这样问题就解决了吗？

生：还需要进行回答：通过计算可以得到最终水面的高度为9公分.

点评：在传统的教学过程中，教师以讲授为主，学生被动地接受一些信息，这样的状态是急需改进的，学生需要通过自己的努力来实现对问题更深入的理解.倘若教师在教学过程中出现一些偏离“标准”的错误，学生有时也会难以发现.教学中，教师不妨让学生多回答，即使回答得不那么出色，也不要紧，让学生体验解题的过程，分析问题产生的原因，才能让学生在心理上认同和接受，从而真正理解解题的实质.

二、问题变化，激活思维

师：通过刚才的问题，我们已经对这样一类问题有一些认识了，下面我们通过一组变式问题进一步研究.

问题1：已知圆锥的侧面展开图所对应的圆心角是120°，它的母线长是12，此时，底面圆的周长为________.

分析：根据圆锥侧面展开图的圆心角与半径（即圆锥的母线的长度）求得的弧长，就是圆锥的底面的周长，然后根据圆的周长公式l=2πr解出r的值即可.

点评：这样的问题考查圆锥的计算.我们需要考虑的是如何通过这样的问题，让学生之间进行不断交流与合作，从而认识到如何解决这样一类问题.正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键，理解圆锥的母线长是扇形的半径、圆锥的底面圆周长是扇形的弧长.

变式1：如图2，圆锥的高h为8cm，底面半径r为6cm，此时圆锥的侧面积为（）cm2.

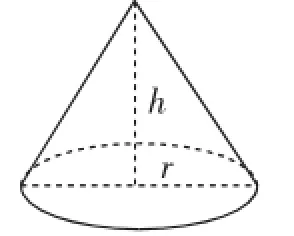
图2

A.30π B.48π C.60π D.80π

解：根据题意可得：h=8，r=6，如果设圆锥母线长为l，则由勾股定理可得l=于是通过侧面展开图的扇形面积公式可得：

所以圆锥的侧面积为60πcm2.

变式2：如图3，这个扇面完全打开，形成的圆心角为120°，母线长为25cm，贴纸部分的宽BD= 15cm，如果将纸扇两面都贴上纸，则贴纸的面积为（）cm2.

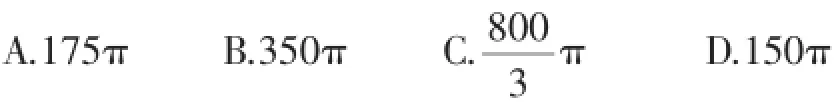
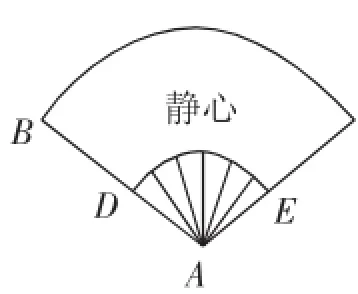
图3

师：同学们，你们如何解决这一问题呢？

生：贴纸部分的面积可以看成两个扇形面积之差.

师：你能具体说一说吗？

生：通过面积公式求差就可以得到结果.

师：请把解题的过程写下来.

点评：通过对话拉近师生之间的距离，帮助学生对问题产生更加深入的认识是十分有必要的.

三、思维提炼，问题进阶

问题2：如图4，在直角△AOB中，∠AOB=90°，OA=3，OB=2，将直角△AOB绕点O顺时针旋转90°后得直角△FOE，将线段EF绕点E逆时针旋转90°后得线段ED，分别以O、E为圆心，OA、ED长为半径画弧AF和弧DF，连接AD，则图中阴影部分的面积是（）.

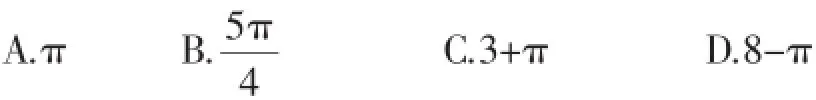
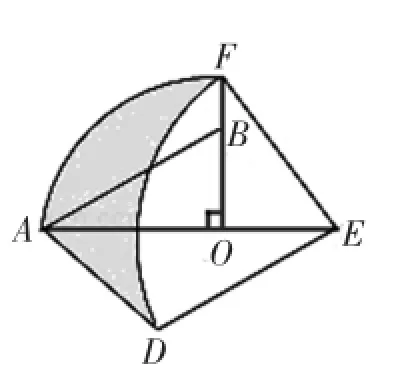
图4

师：如何解答？

生：可以通过面积转化来解决.

师：具体说说看.

生：我想这样来解决：如图5，作DH⊥AE于H，根据勾股定理求出AB，根据阴影部分面积=△ADE的面积+△EOF的面积+扇形AOF的面积-扇形DEF的面积，就可以得出最后的结果.

师：接下来，我请一位同学上来板书.

学生板书如下：作DH⊥AE于H.由∠AOB=90°，OA= 3，OB=2，得由旋转的性质可知OB=2.阴影部分的面积=△ADE的面积+△EOF的面积+扇形AOF的面积-扇形DEF的面积

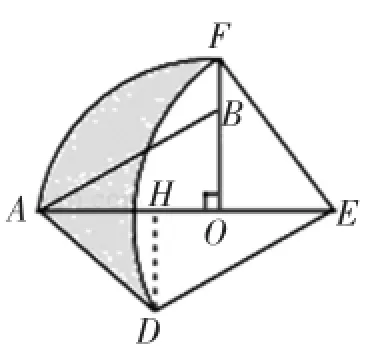
图5

师：这样的解答过程非常到位，下面我们来看一个阴影部分面积的变形问题，再来作进一步思考.

变式：如图6，从一张腰长为60cm、顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD，用此剪下的扇形铁皮围成一个圆锥的侧面（不计损耗），则该圆锥的高为（）cm.

图6

这个问题可以通过如下的师生之间的交流互动来实现：

师：大家怎么看待这个问题？

生：通过等腰三角形的性质来解决问题.

师：具体谈一谈.

生：先求半径，然后通过勾股定理计算高.

师：非常好！那么，你能说出这一问题考查的实质是什么吗？

生：这个问题考查圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长.

师：回答非常到位！通过这样的问题分析，我们向中考又迈进了坚实的一步.

点评：学生对知识的学习必须有优化的过程，要注重让学生自己总结解题方法，使他们能在知识的学习中进行高层次的思维.在这里，教学设计让学生更多地展现自己的智慧，不断地将学习的主动权交给学生，让他们剖析问题的实质，解决问题并表述自己的观点，自主“构建”符合其认知水平的知识体系.

四、对中考视角下的对话教学的认识

中考评价本身带有非常明确的指向性，这样的指向性功能非常有利于日常的解题课的教学.通过师生之间的有效对话可以看到，对思路的探索过程无疑是解题教学的重中之重，在课堂教学的过程中，应当多花时间在这一类问题上.教师对学生的指导，一方面体现在对问题的把握上，同时也体现在问题的取舍之中.对话是为了更好地促进教学，教学中教师一定要学会收与放，放开手不急于帮助，收回来不急于解答，将更多的空间给学生，帮助他们更快地成长.