初中数学拓展性课程的“哺育”与“反哺”——“平方根”与“无理数的由来”对比研究

☉浙江杭州市富阳区永兴中学 许灵嘉

初中数学拓展性课程的“哺育”与“反哺”
——“平方根”与“无理数的由来”对比研究

☉浙江杭州市富阳区永兴中学 许灵嘉

拓展性课程开发的兴起是伴随着新一轮基础教育课程改革出现的新生事物.2015年《浙江省教育厅关于深化义务教育课程改革的指导意见》指出：义务教育课程分为基础性课程和拓展性课程.基础性课程指国家和地方课程标准规定的统一学习内容；拓展性课程指学校提供给学生自主选择的学习内容，是对基础性课程的补充与拓展.

笔者认为，基础性课程与拓展性课程犹如大树与枝叶.基础性课程提供主干作用，滋养着拓展性课程，对拓展性课程的开发和实施起到指导作用；拓展性课程丰富了基础性课程的内容，也为基础性课程的学习服务.那么，如何运用基础性课程指导拓展性课程的设计、开发，拓展性课程又如何为基础性课程服务呢？笔者通过一节成功的基础性课程“平方根”教学与笔者在所在学校开设的拓展性课程“数学史拾趣”中“无理数的由来”一课进行对比探究.

一、明月松间照：基础性课程对拓展性课程的“哺育”作用

（一）基础性课程教学是拓展性课程教学的“指南针”.

基础性课程的教学经过长时间的研究、实践，有较为完善的体系，而拓展性课程作为新生事物，其教学处于探索阶段.笔者认为，拓展性课程不是一门“想怎么教就怎么教”的课程，它也需要形成教学方法，基础性课程的教学为其提供了“指南针”作用.

1.教学程序.

在“平方根”教学中，笔者运用的是概念教学的一般程序：

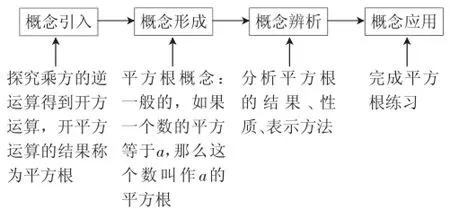
图1 “平方根”教学程序

在“无理数的由来”教学中，笔者借鉴“平方根”的教学程序进行：

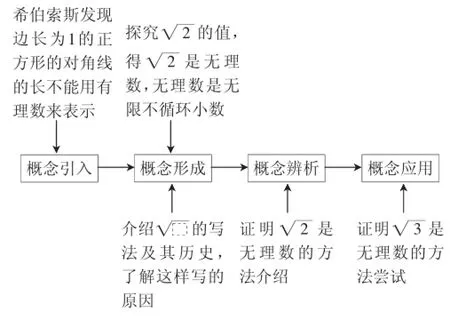
图2 “无理数的由来”教学程序

笔者在拓展性课程“无理数的由来”中运用了基础性课程“平方根”概念教学的教学程序，使教学过程完整、有序.

两者的对比研究：

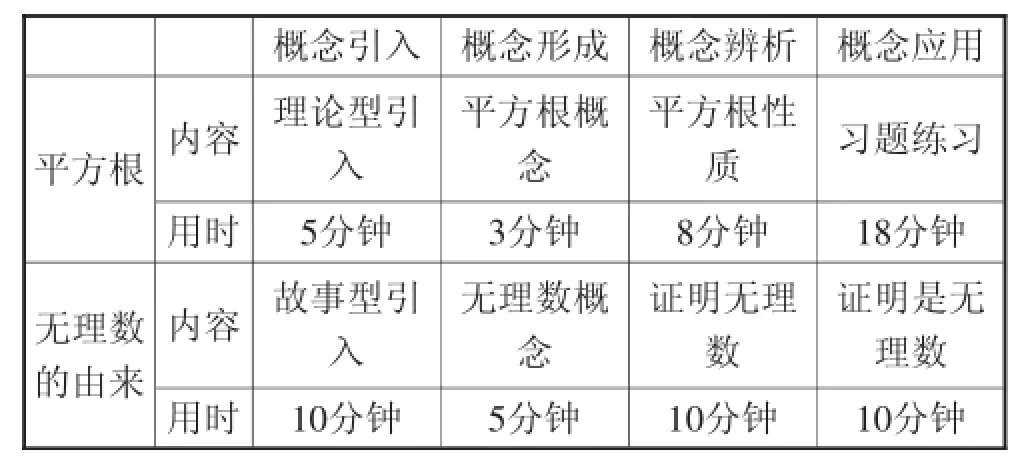
表1：“平方根”与“无理数的由来”教学程序对比表

由此可见，基础性课程的教学程序为拓展性课程提供指导，而在具体的程序中，基础性课程更注重知识的理解和应用，拓展性课程可以更注重知识的由来发展及趣味性体现.

2.教学方法.

“平方根”概念辨析环节教学实录：

一般地，如果一个数的平方等于a，那么这个数就叫作a的平方根.如果x2=a，则x叫作a的平方根.

师：在这个定义里，你还能读出更多的信息来吗？你觉得这里的a是一个什么样的数？

生1：a是一个非负数.

师：a为什么是非负数？

生1：负数的平方是正数，正数的平方依然是正数，还要考虑0的平方是0，所以一个数的平方一定是非负数.

师：非常厉害！进一步，这里还有一个字母，你认为x是什么情况？

生2：x可能是正数、负数或0.

师：是不是同时出现的？

生3：不是，正数有两个平方根，一个是正数，一个是负数，0只有一个平方根，就是0.

师：你的意思就是根据a的取值分情况来看.x是一个数或者是两个数，如果是两个数，一正一负什么关系？

生（七嘴八舌）：互为相反数.

师：看，我们又分析得到了两个字母的取值问题，所以我们要善于发现概念背后的隐含信息，把它读出来.

笔者在“平方根”的概念教授过程中花了大量的时间在概念的剖析上，以概念中的两个字母为切入点，分析两个字母的取值，得到了概念的隐含条件且顺其自然地得到了平方根的性质.这样的概念教学是学生依据自己已有的知识和经验主动加以建构得到的，体现了学生的主体地位，又深入了概念本质.这为学生以后的概念学习提供了方法指导，既让学生对数学知识有了深刻的认知，又培养了学生数学学习的能力.

由此可见，基础性课程的教学已有理论支持和方法指导，在日常的教学中，一线教师已基本掌握基础性课程的教学方法，所以拓展性课程的教学需要借鉴、依据基础性课程的教学方法.比如，概念教学要深入概念本质，不能因为是拓展性课程就一带而过；拓展性课程也需要以学生为主体，使学生根据已有知识经验主动地对知识进行建构；基础性课程需要培养学生提出问题、分析问题、解决问题的能力，拓展性课程更是学生提出、分析、解决问题的最好平台.

（二）数学思想方法的渗透是拓展性课程的“风向标”.

初中数学蕴含着大量的数学思想与方法，这些是数学学习最本真的东西，在基础性课程中隐性地体现其中.

“平方根”教学片段实录1：

师：乘方的逆运算是什么？我们一起来研究一下.首先我们来回忆一下乘方运算，xn中，x称为底数，n称为指数，整个结果称为幂.在乘方运算中，比如，x的平方、立方、四次方……如果要一一研究，特别难，那我们怎么办？

生（齐）：挑一个.

师：你挑哪个？

生（齐）：平方，简单.

“平方根”教学片段实录2：

师：乘方的逆运算有吗？我们先来看加法的逆运算是怎么产生的.加法运算中有加数、和，已知一个加数与和，求另一个加数，产生了减法.那么乘除呢？

生1：乘法运算中已知一个因数和积，求另一个因数，产生了除法.

师：那么乘方呢？加法运算中我们把一个加数变成问号产生逆运算，乘法运算中我们把一个因数变成问号产生逆运算，乘方运算中我们把什么变成问号？

生（齐）：底数.

师：求指数的运算我们高中将学习——对数，求底数的运算我们今天来学习，也就是乘方的逆运算——开方.

“平方根”教学片段实录3：

观察思考：两种运算有什么不同？

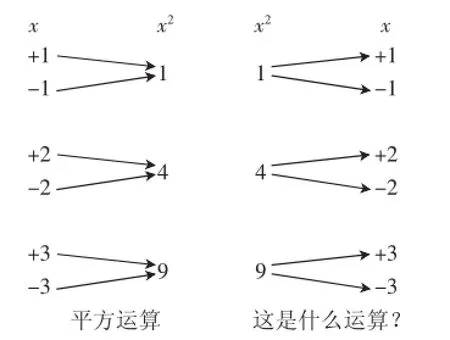
图3

“无理数的由来”教学片段实录1：

师：通过计算我们发现，我们可以得到一系列越来越接近的近似值，但是不能做到底，这与我们学过的很像，它们都是无限不循环的小数，我们把这种无限不循环小数叫作无理数.你还能举出类似的无理数吗？

“无理数的由来”教学片段实录2：

(二)离合词“A了个B”与网络语“A了(嘞)个B”在不同的语体中使用。前者一般在书面语体中或是在正规场合的口语中出现。而后者则主要出现在网络即时工具聊天，网络游戏或者网络论坛中，不过现在也开始“入侵”到非正规场合的口语中，用以表示幽默和时髦。如：

两者对比研究：“平方根”三个教学片段分别在教学过程中渗透了从一般到特殊的数学研究方法、类比的数学思想、图表探究法等数学思想方法，基础性教学对数学思想方法的渗透可见一斑.“无理数的由来”中，从特殊的的研究、得到一般的无理数的概念，渗透了从特殊到一般的数学思想方法；模仿是无理数的证明方法证明是无理数运用了类比思想；又由特殊的无理数证明可以归纳出证明一般的“开不尽方”产生的无理数的方法.

显而易见，是基础性课程对数学思想方法的渗透方式指导着拓展性课程如何在教学过程中体现数学思想方法.而拓展性课程的教学更是渗透数学思想方法的最好平台.

（三）短片式阅读为拓展性课程提供“活水源”.

在“平方根”教学中，涉及根号的学习，笔者通过查阅根号的演变历史，在教学中以短片式阅读的方式向学生介绍了根号的写法：

平方根号曾经用拉丁文“Radix”（根）的首尾两个字母合并起来表示.1840年前后，德国人用一个点“.”来表示平方根.1525年，路多尔夫在他的代数著作中，首先采用了“”表示根号，“”是由拉丁字母“r”变化而来的.十七世纪初叶，法国数学家笛卡儿在他的《几何学》中，第一次使用现今的“这是出于什么考虑呢？有时候被开方数的项数较多，为了避免混淆，笛卡尔就用一条横线把这几项连起来，因此我们的根号书写中横线长短要恰当.

这样的教学素材为笔者的拓展性课程的开展提供了“活水源”，在“无理数的由来”一课中，笔者将“根号的历史”作为一块内容展开进行教学：

根号的由来

古时候，埃及人用记号“┌”表示平方根.印度人在开平方时，在被开方数的前面写上ka.

1840年前后，德国人用一个点“.”来表示平方根，两点“..”表示4次方根，三个点“...”表示立方根，比如，.3、..3、...3就分别表示3的平方根、4次方根、立方根.

与此同时，有人采用“根”字的拉丁文radix中第一个字母的大写R来表示开方运算，并且后面跟着拉丁文“平方”一字的第一个字母q，或“立方”的第一个字母c，来表示开的是多少次方.

直到十七世纪，法国数学家笛卡尔（1596—1650年）第一个使用了现今用的根号“在一本书中，笛卡尔写道：“如果我想求a2+b2的平方根，就写作，如果想求a3+b3+abc的立方根，则写作求

这是出于什么考虑呢？有时候被开方数的项数较多，为了避免混淆，笛卡尔就用一条横线把这几项连起来，前面放上根号就为现时根号形式.

立方根符号出现得很晚，一直到十八世纪，才在一书中看到符号的使用，比如25的立方根用表示.以后，诸如等形式的根号渐渐使用开来.

由此可见，一种符号的普遍采用是多么地艰难，它是人们在悠久的岁月中，经过不断改良、选择和淘汰的结果，它是数学家们集体智慧的结晶，而不是某一个人凭空臆造出来的，也绝不是从天上掉下来的.

两者对比研究：基础性课程的数学史渗透或短片式阅读的呈现方式更为简洁，它所起到的作用主要是引入，激发学生一定的学习兴趣，拓宽学生的视野.“平方根”中根号的演变历史介绍另一用途是由此强调了根号书写中横线的用处及写法.基础性课程介绍的这些数学史、短片式阅读往往可以成为拓展性课程的设计开发的“活水源”，拓展性课程可以在此基础上对内容、形式进行拓展，形成自身的教学内容.

基础性课程的依据主要是课程标准和教材.由于课程改革，目前的教材中有大量的短片式阅读为拓展性课程的开发提供了“活水源”.笔者所在学校将浙教版数学教材提供的短片式阅读进行了简单整理，这些基础性课程的内容已经成为或即将成为开展拓展性课程教学的“活水源”，运用到学生开设的拓展性课程的开发和实施中.

1.课题学习与设计题.

数学来源于生活又服务于生活.现实生活中有大量与时代发展同步的数学素材，开发这些数学素材应用于拓展性课程的教学，既可以加深学生对数学知识的理解，又能提升学生的数学应用意识.教材中的课题学习与设计题为我们提供了范例.

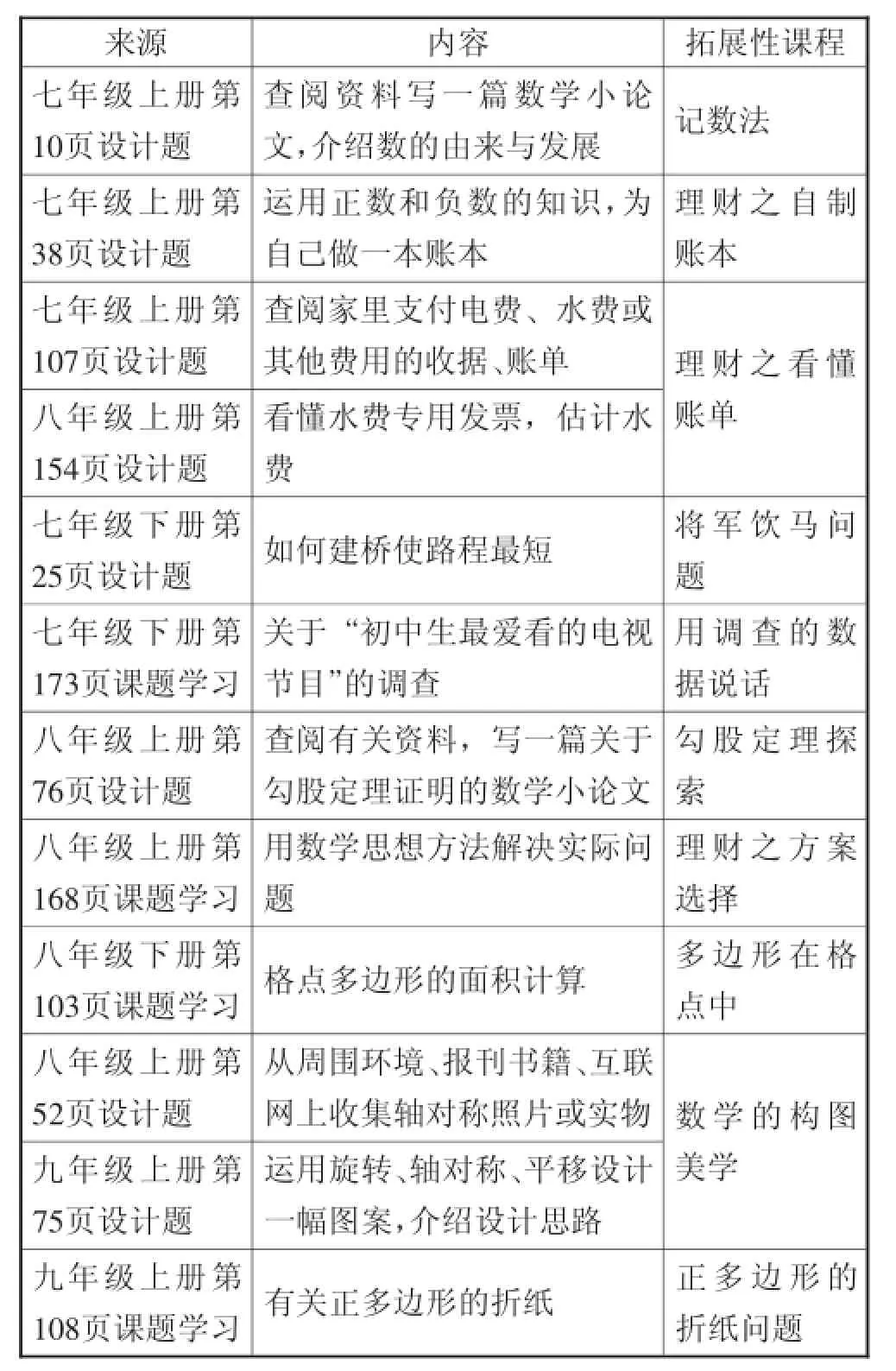
表2

2.探究活动或习题.

教材中的探究活动或习题往往与所学内容相关，有一定的探究价值又具有一定的趣味性，由此可以开发由学生主体参与的问题发现、探究、解决、反思、归纳等形式的拓展性课程，通过运用数学的基本思想解决问题，让学生感悟数学思想，归纳和形成解题方法和策略，激发学生数学学习的兴趣，提升学生的数学素养.

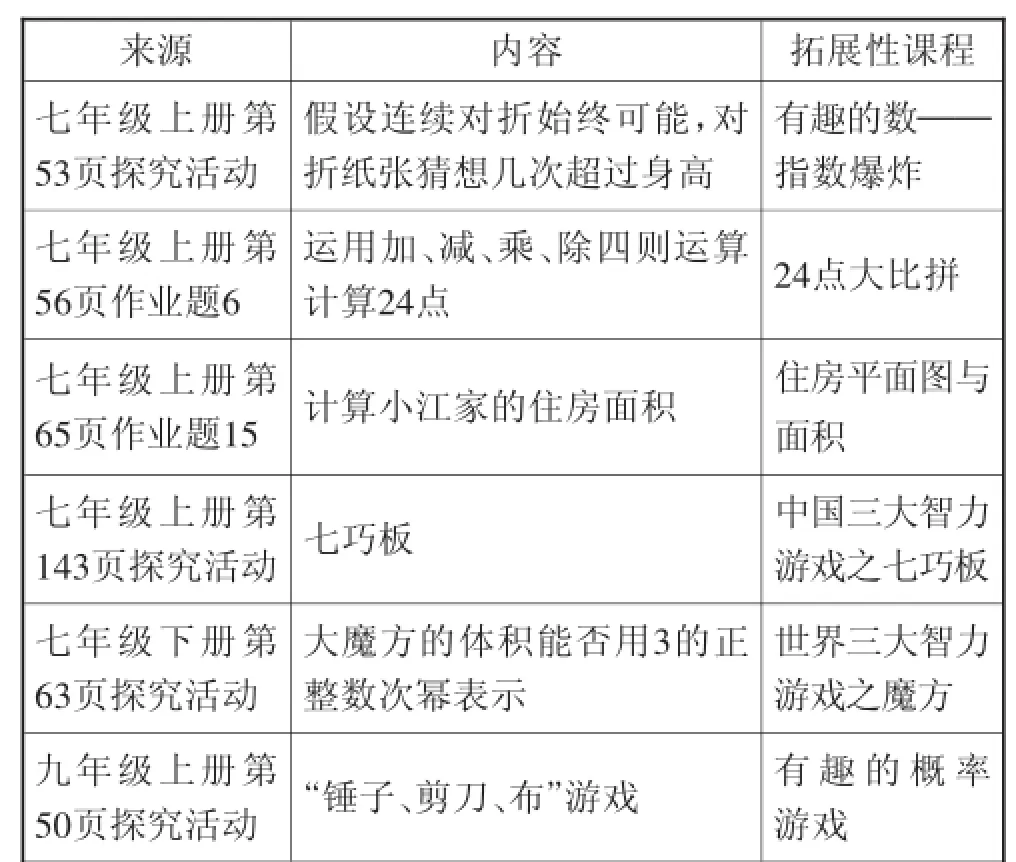
表3

3.数学史阅读.

数学史是研究数学思想和方法产生、发展及其规律的科学，有关的数学的重大历史事件、重要的数学成果及其研究过程、数学大师的介绍等都能有机融入数学课程.数学史的渗透有助于学生用发展的眼光看数学、用坚毅的品质研究数学、用大家的眼光理解数学.

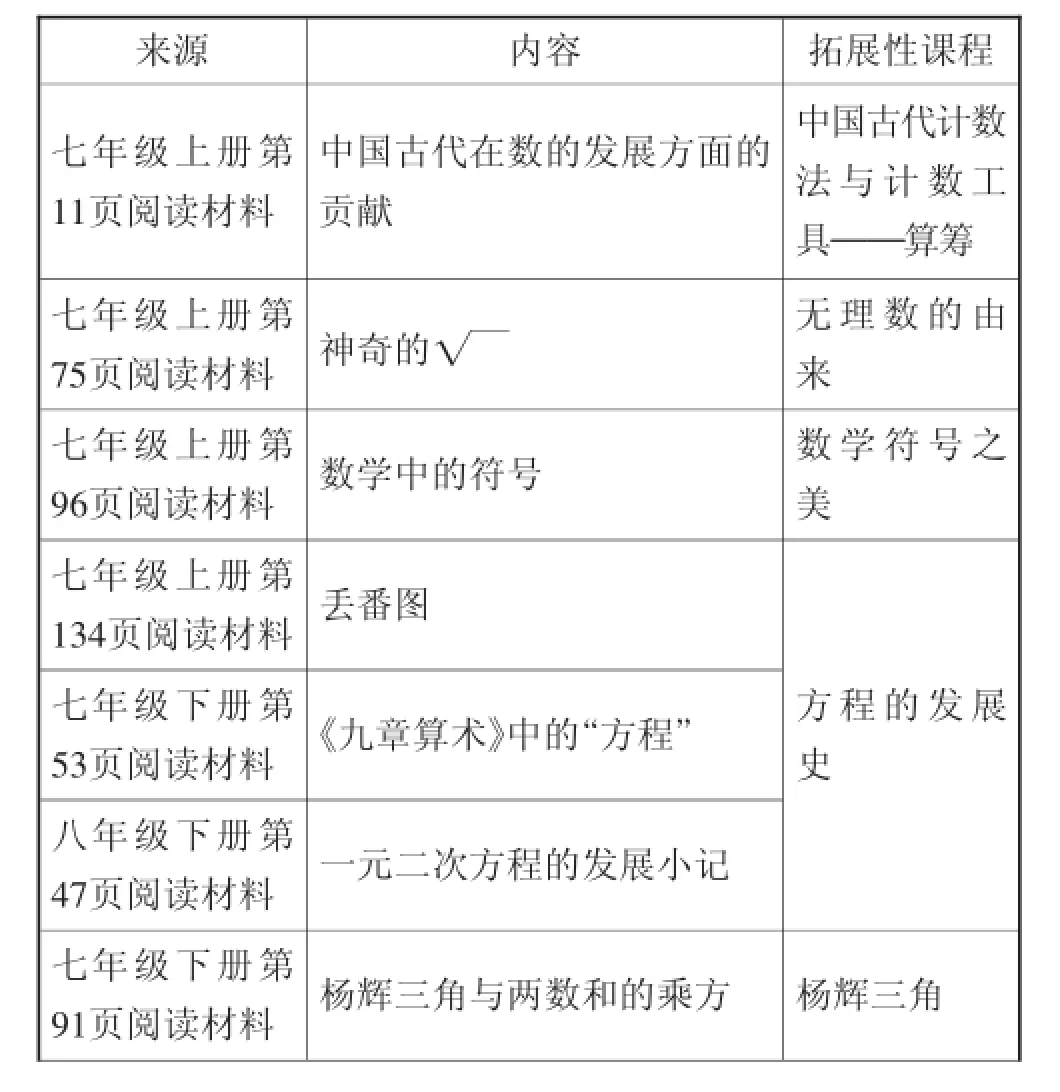
表4

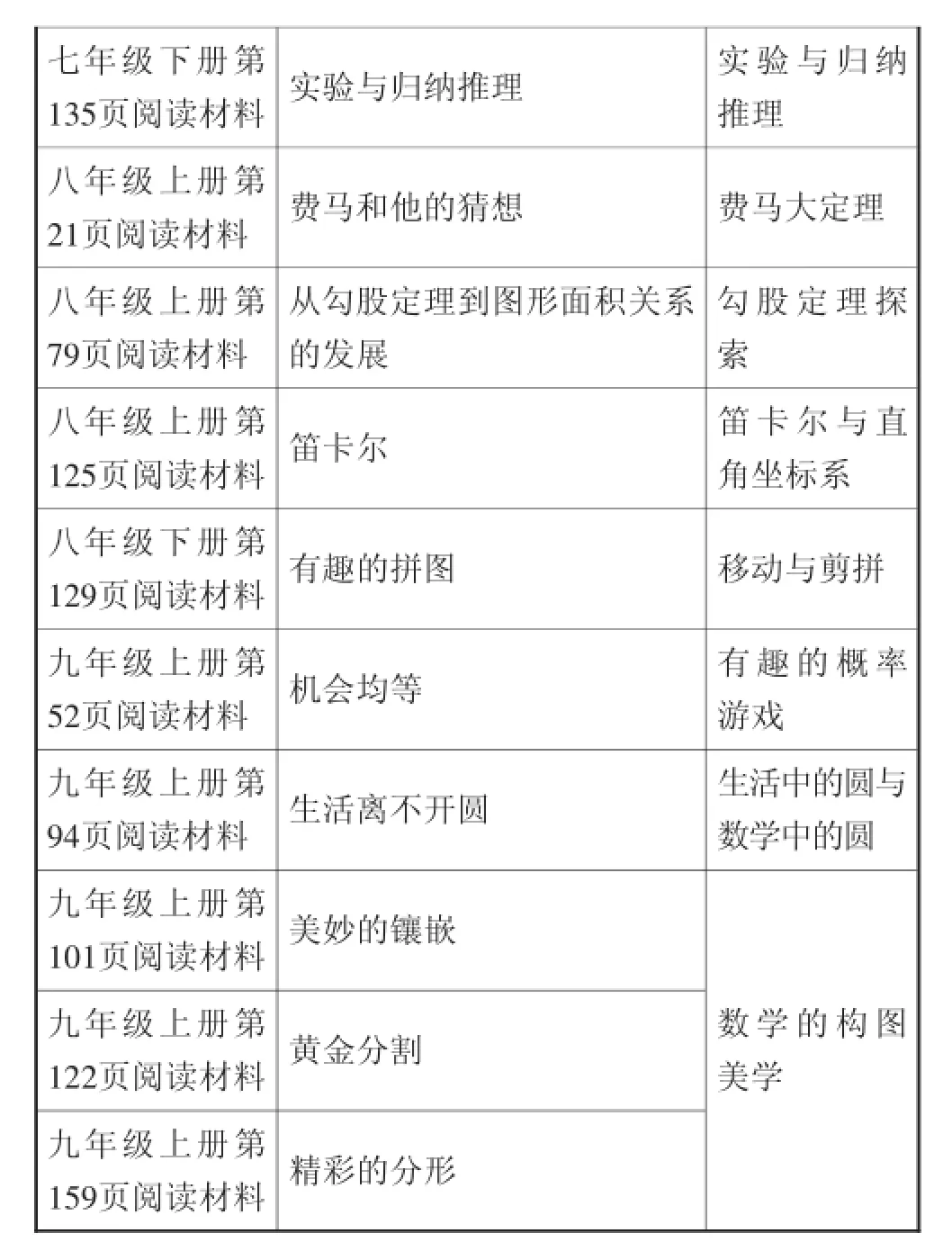
七年级下册第135页阅读材料八年级上册第21页阅读材料实验与归纳推理实验与归纳推理费马和他的猜想费马大定理八年级上册第79页阅读材料从勾股定理到图形面积关系的发展勾股定理探索八年级上册第125页阅读材料八年级下册第129页阅读材料九年级上册第52页阅读材料笛卡尔笛卡尔与直角坐标系有趣的拼图移动与剪拼机会均等有趣的概率游戏九年级上册第94页阅读材料生活离不开圆九年级上册第101页阅读材料九年级上册第122页阅读材料九年级上册第159页阅读材料美妙的镶嵌黄金分割精彩的分形生活中的圆与数学中的圆数学的构图美学

二、清泉石上流：拓展性课程对基础性课程的”反哺“作用

“有兴趣的同学可以课外自己去研究.”这是我们数学教师提及教材中的探究活动、设计题、阅读材料或布置课外实践活动作业时常用的一句话.试问：学生课外真的去“研究”了吗？有多少学生会去“课外研究”？他们又是否有时间、有能力去自行研究呢？作为教师，我们需要关注这些问题，真正为学生进行“课外探究”创造条件.拓展性课程为这样的”课外探究“创造了条件.拓展性课程由基础性课程“哺育”，又“反哺”基础性课程的教学和学习.

（一）激发学生的兴趣和成就动机.

有趣的数学实验、生动的数学探究、精彩的数学历史等都可以很大程度上激发学生的学习兴趣，让学生明白数学并不是一门枯燥呆板的学科，而是一门不断发展、可以不断探究的生动有趣的学科.在拓展性课程的学习中，评价可以多元化，同时，实验、探究、阅读等过程中每个人都有收获，这使学生获得数学学习的成就感，从而由于这种成就动机而更加热爱数学学习.

（二）促进学生的数学思考和理解.

新课程强调让学生经历数学思维过程，体验解决问题策略的多样性.由于课程内容、时间的限制，基础性课程无法给学生提供调查、探究、实验等较大型数学课题学习的平台，比如，调查“初中生最喜爱的电视节目”，七巧板、魔法、折纸等实验，拓展性课程可以打破这种局限，提供这一平台，让学生参与问题的发现、探究、解决、反思、归纳等过程，促进学生的数学思考和对数学问题的理解.

（三）帮助学生形成正确的数学观.

数学并不是单纯的知识和习题，并不是坐在教室里耳朵听、动脑思考、动笔做的课程，数学还有对问题的探究，还有调查和数据整理，还有生活的运用，还有美图的构建，还有游戏，还有理财等.学习数学并不是学会做题和考试，还需要走出课堂深入生活.数学定理、公式并不是写在书本上然后去记忆、背诵，还需要用严谨的态度和思维方式去探究、发现，还需要学会提出问题、分析问题、解决问题等.拓展性课程的设置可以通过这些方式帮助学生形成正确的数学观.

（四）发展理性精神和创造性思维.

在数学阅读中，学生可以知道当“万物皆数”成为毕达哥拉斯学派的信条时，希伯索斯却提出了无理数的存在，成为“叛逆者”而被葬身大海，由此产生了数学史上第一次数学危机；芝诺悖论和理发师悖论分别产生了数学史上的第二次、第三次数学危机.数学史的拓展性课程中可以介绍数学史上三次危机的产生与解决，介绍悖论，介绍未被证明的定理等，这些对基础性课程的补充让学生用发展的眼光看数学，鼓励学生锲而不舍地追求真理并不断创新.

1.浙江省教育厅.浙江省教育厅关于深化义务教育课程改革的指导意见［Z］.浙教基〔2015〕36号.

2.王冰.教材分析——从宏观到微观［J］.中学数学教学参考，2011（5）.

3.史宁中.义务教育数学课程标准（2011年版）解读［M］.北京：北京师范大学出版社，2012.

4.李红婷.课改新视域：数学史走进新课程［J］.课程·教材·教法，2005（9）.