融合对立学习的混合灰狼优化算法*

王 敏，唐明珠

1.湖南机电职业技术学院 信息工程学院，长沙 410151

2.湖南大学 计算机与通信学院，长沙 410082

3.长沙理工大学 能源与动力工程学院，长沙 410114

融合对立学习的混合灰狼优化算法*

王 敏1,2+，唐明珠3

1.湖南机电职业技术学院 信息工程学院，长沙 410151

2.湖南大学 计算机与通信学院，长沙 410082

3.长沙理工大学 能源与动力工程学院，长沙 410114

灰狼优化算法；Rosenbrock搜索；对立学习

1 引言

群体智能优化算法源于对自然界中生物群体的一些行为机制的模拟，通过生物群体中个体之间的相互合作所表现出的智能行为进行迭代搜索。与传统优化方法相比，群体智能优化算法通常具有原理简单，需调整的参数少，支持分布式并行计算，编程容易实现，无需问题的梯度信息，较强的全局搜索能力等特点，因此被广泛应用于函数优化、参数估计、组合优化、神经网络训练、自动控制、图像处理、路径规划等多个领域。典型的群智能优化算法有粒子群优化（particle swarm optimization，PSO）算法[1]、蚁群优化（ant colony optimization，ACO）算法[2]、人工蜂群（artificial bee colony，ABC）算法[3]等。

2014年，Mirjalili等人[4]借鉴灰狼群体捕食行为的特性，提出一种新型群体智能优化算法，即灰狼优化（grey wolf optimization，GWO）算法。GWO算法主要通过狼群追踪、包围、追捕、攻击猎物等过程来达到优化搜索的目的。GWO算法具有原理简单，需要调整的参数少，并行性，编程容易实现，有较强的全局搜索能力等特点。在函数优化方面，GWO算法比PSO算法、引力搜索算法（gravitational search algorithm，GSA）和差分进化（differential evolution，DE）算法具有更快的收敛速度和较好的收敛精度[4]。因此，GWO算法被广泛应用于电力系统[5]、传感器训练[6]、直流电机最优控制[7]、经济调度[8]、特征子集选择[9]等领域中。

然而，与其他群体智能优化算法类似，GWO算法同样也存在后期收敛速度慢，求解精度不高，易出现早熟收敛现象等缺陷。因此，研究人员从不同角度对GWO算法进行改进以提高其寻优性能。文献[10]将动态进化种群（evolutionary population dynamics，EPD）算子嵌入到GWO算法中，用于加快算法收敛速度和增强其局部搜索能力。文献[11]提出一种改进GWO算法用于训练高斯径向基函数神经网络。文献[12]结合差分进化的搜索能力，提出一种混合GWO算法用于函数优化和三维堆叠芯片的测试调度。文献[13]提出一种改进GWO算法用于求解约束优化问题，在改进算法中，引入佳点集初始化种群个体，对当前最优个体执行Powell局部搜索。

针对标准GWO算法的缺点，本文利用对立学习策略取代随机初始化生产初始种群；为了增强局部搜索能力和加快收敛速度，对当前群体中最优个体进行Rosenbrock局部搜索；对当前最优个体执行精英对立学习策略以避免算法出现早熟收敛现象，提出一种混合GWO算法。

2 灰狼优化算法

2.1 灰狼群体捕食行为

灰狼是顶级食肉动物，其生活方式大多以群居为主，构建了灰狼种群等级金字塔，并具有严格的等级管理制度，如图1所示。

Fig.1 Hierarchy of grey wolf population图1 灰狼种群等级金字塔示意图

金字塔第一层为种群中的头狼称为α，主要负责群体各项决策事务；金字塔第二层称为β，协助α做出管理决策；金字塔第三层为δ，δ听从α及β的指令；金字塔最底层称为ω，主要负责平衡种群内部关系。

灰狼的种群等级在实现群体高效捕杀猎物的过程中发挥着至关重要的作用。捕食过程由α带领完成，首先狼群以团队模式搜索、跟踪、靠近猎物，然后从各个方位包围猎物，当包围圈足够小且完善时，狼群在α的指挥下由猎物最近的β、δ展开进攻，在猎物逃跑时，其余个体进行补给，实现群狼包围圈的跟随变换移动，从而对猎物不断实施各个方向的攻击，最终捕获猎物。

2.2GWO算法描述

在GWO算法中，由α、β、δ执行追捕行为，ω跟随前3者进行猎物跟踪围剿，最终完成捕食任务。利用GWO算法求解连续函数优化问题时，假设灰狼种群中的灰狼数目为N，搜索空间为d维，其中第i只灰狼在d维空间中的位置可表示为xi=(xi1,xi2,…,xid)，种群中当前最优个体记为α，将适应度值排名第二及第三的对应个体记为β和δ，剩余个体记为ω，猎物的位置对应于优化问题的全局最优解。

在捕食过程中，灰狼群体首先根据式（1）对猎物进行包围：

其中，Xp(t)表示第t代时猎物的位置；X(t)表示第t代时灰狼个体的位置；常数C为摆动因子，由式（2）决定：

式中，r1为[0,1]之间的随机数。

利用式（3）进行灰狼位置更新：

其中，A为收敛因子，由式（4）决定：

式中，r2为[0,1]之间的随机数；a随着迭代次数增加从2线性递减到0。

狼群中个体跟踪猎物方位的数学描述如下：由式（5）～（10）计算出群内其他灰狼个体与α、β、δ的距离，然后由式（11）即可综合判断出个体向猎物移动的方向。

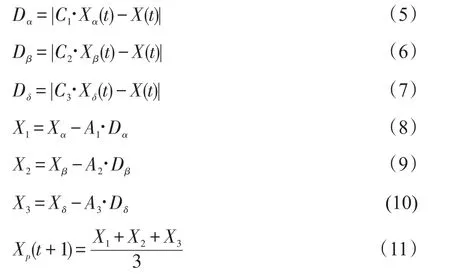
3 混合灰狼优化算法

3.1 基于对立学习的种群初始化

与其他群体智能优化算法一样，基本GWO算法在迭代前同样采用随机初始化种群个体。由于事先对全局最优解没有任何先验知识，初始种群应均匀地覆盖在搜索空间中。对基于种群迭代的智能优化算法来说，最优保存策略是将上一代种群中的优良个体保存到下一代种群；若初始种群中的优良个体较少，则会直接影响算法的收敛。另外，初始种群的优劣还会影响算法的收敛速度。因此，本文采用对立学习策略[14]来产生初始种群，即同时产生当前个体及相应的对立个体，然后比较选择适应度值较好的个体作为初始种群个体，从而提高算法的搜索效率。

对立学习策略是由学者Tizhoosh[14]于2005年提出的，目前已在遗传算法（genetic algorithm，GA）、PSO算法、差分进化算法、ACO算法、生物地理学优化（biogeography-based optimization，BBO）算法等群体智能优化算法中得到了成功的应用。

定义1（对立点）假设在[l,u]上存在数x，则x的对立点定义为x′=l+u-x。将对立点的定义扩展到n维空间，设 p=(x1,x2,…,xn)为n维空间中的一个点，其中xi∈[li,ui]，i=1,2,…,n，则其对立点为 p′= (x1′,x2′,…,xn′)，其中xi′=li+ui-xi。

根据上述定义，基于对立学习策略的种群初始化步骤如下：

（1）在搜索空间中随机初始化N个灰狼个体位置 xij(i=1, 2,…,n,j=1, 2,…,N)作为初始种群 RP，N为种群规模。

（2）根据定义1，初始种群RP中的每个灰狼个体x的对立个体x′构成对立种群OP。

（3）合并种群RP和OP，将其2N个灰狼个体按照适应度值进行升序排序，选取适应度值前N个灰狼个体作为初始种群。

3.2 Rosenbrock搜索方法

Rosenbrock搜索[15]是一种用于无约束优化的直接方法，它不需问题的梯度信息，具有强大的局部搜索能力。其搜索过程包括两个阶段，即探测和构造新的搜索方向。

第一阶段 探测阶段。

步骤1给定初始点x(1)∈Rn，取坐标方向作为单位正交方向d(1),d(2),…,d(n)，步长，缩减因子 β∈(-1,0)，扩大因子α＞1，允许误差ε＞0。令y(1)=x(1)，k=1，j=1，δi=δ(0)i(i=1,2,…,n)。

步骤2 若 f(y(j)+δjd(j))＜f(y(j))，则 y(j+1)=y(j)，δj: = αδj，否则，y(j+1)=y(j)，δj: =βδj。

步骤3若 j＜n，则 j:=j+1，转步骤2；否则，转步骤4。

步骤4 若 f(y(n+1))＜f(y(1))，则 y(1)=y(n+1)，j=1，转步骤2；若 f(y(n+1))=f(y(1))，则转步骤5。

步骤5若 f(y(n+1))＜f(y(k))，则转步骤6；否则，若对于所有 j，|δj|≤ε成立，则计算停止，x(k)作为近似最优解；否则，令y(1)=y(n+1)，j=1，转步骤2。

步骤 6 设 x(k+1)=y(n+1)，若 ||x(k+1)-x(k)||≤ε，则将x(k+1)作为近似极小值，计算停止；否则，转步骤7。

第二阶段 构造新的搜索方向。

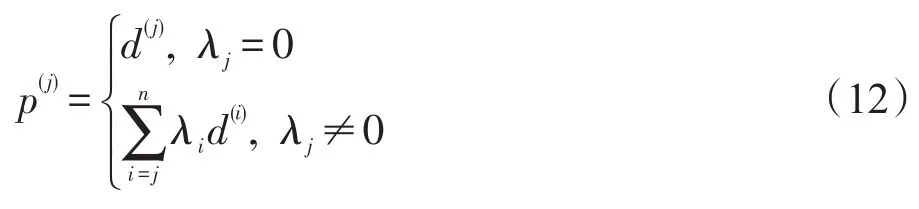
采用Gram-Schmidt方法将{p(j)}正交化，令

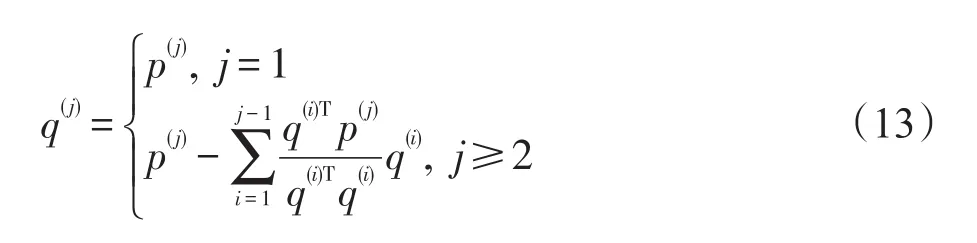
然后单位化，令

获得n个新的正交搜索方向。

步骤8 令d(j)=dˉ(j)，δj=δ(0)j(j=1,2,…,n)，y(1)=x(k+1)，k:=k+1，j=1，返回步骤2。

3.3 精英对立学习策略

利用GWO算法在求解优化问题时，找到全局最优解是其最终的目标。在GWO算法的进化过程中，尤其是进化后期，所有灰狼个体均向决策层区域逼近，从而导致群体多样性损失，收敛速度明显变慢或停止，进而陷入局部最优，这也是群体智能优化算法的固有特点。

由文献[14]可知，对立学习策略能较好地扩大群体的搜索范围，开采出新的搜索区域，增强群体的多样性，利用其与群体智能优化算法混合，可提高算法的全局搜索能力和避免算法出现早熟收敛现象。因此，本文对决策层中个体执行精英对立学习策略。

由定义2可知，γ为[0,1]之间服从均匀分布的随机数，当γ取不同的数值时，由当前灰狼群体中决策层3个个体可产生多个不同的精英对立个体，从而可有效地提高群体的多样性，避免算法陷入局部最优。

3.4HGWO算法步骤

步骤1初始化算法参数。种群规模N，最大迭代次数，在搜索空间中随机生成a、A、C等参数。

步骤2在搜索空间中利用2.1节所描述的对立学习策略产生包含N个灰狼个体的初始种群，令t=1。

步骤3计算群体中每个灰狼个体的适应度值，并将适应度值进行排序，记录最优适应度值及对应位置。

步骤4将适应度值排列前3位的灰狼个体位置分别记为Xα、Xβ和Xδ，作为决策层。

步骤5由式（5）～（7）计算群体中其他灰狼个体与Xα、Xβ和Xδ的距离，并根据式（8）～（11）更新每个灰狼个体的位置。

步骤6利用2.2节所描述的Rosenbrock搜索方法对当前最优灰狼个体进行局部精确搜索。

步骤7对决策层个体Xα、Xβ和Xδ执行2.3节所描述的精英对立学习策略以产生新的个体。

步骤8更新a、A、C等参数的值。

步骤9判断灰狼群体是否满足收敛条件，若是，则算法结束，输出最优解；否则，令t=t+1，返回步骤3。

4 仿真实验及分析

4.1 测试函数

为了检验本文提出的HGWO算法的寻优性能，选取6个标准测试函数进行仿真实验，6个测试函数的表达式如下。

在上述6个测试函数中，f1、f2和 f3为单峰函数，f4、f5和 f6为多峰函数，函数的维数均设置为30，6个函数的全局最优值均为0。

4.2与标准GWO和GWO-DE算法的比较

利用HGWO算法对6个标准测试函数进行求解，并与标准GWO算法以及混合GWO与差分进化（记为GWO-DE）算法[12]进行比较。3种算法参数如下：种群规模N均设置为50，最大迭代次数均设置为1 000，收敛精度设置为1E-06。所有仿真实验均在Intel Core Quad，CPU：Q8300，2 GB内存，2.50 GHz主频的计算机上实现，程序采用Matlab7.0语言实现。

6个测试函数在上述参数设置的条件下，采用GWO和HGWO算法分别独立运行30次，记录其最优值、平均值、最差值和标准差，并与GWO-DE算法的结果进行比较，结果如表1所示。为了增加其可信度，GWO-DE算法的结果直接来源于参考文献。

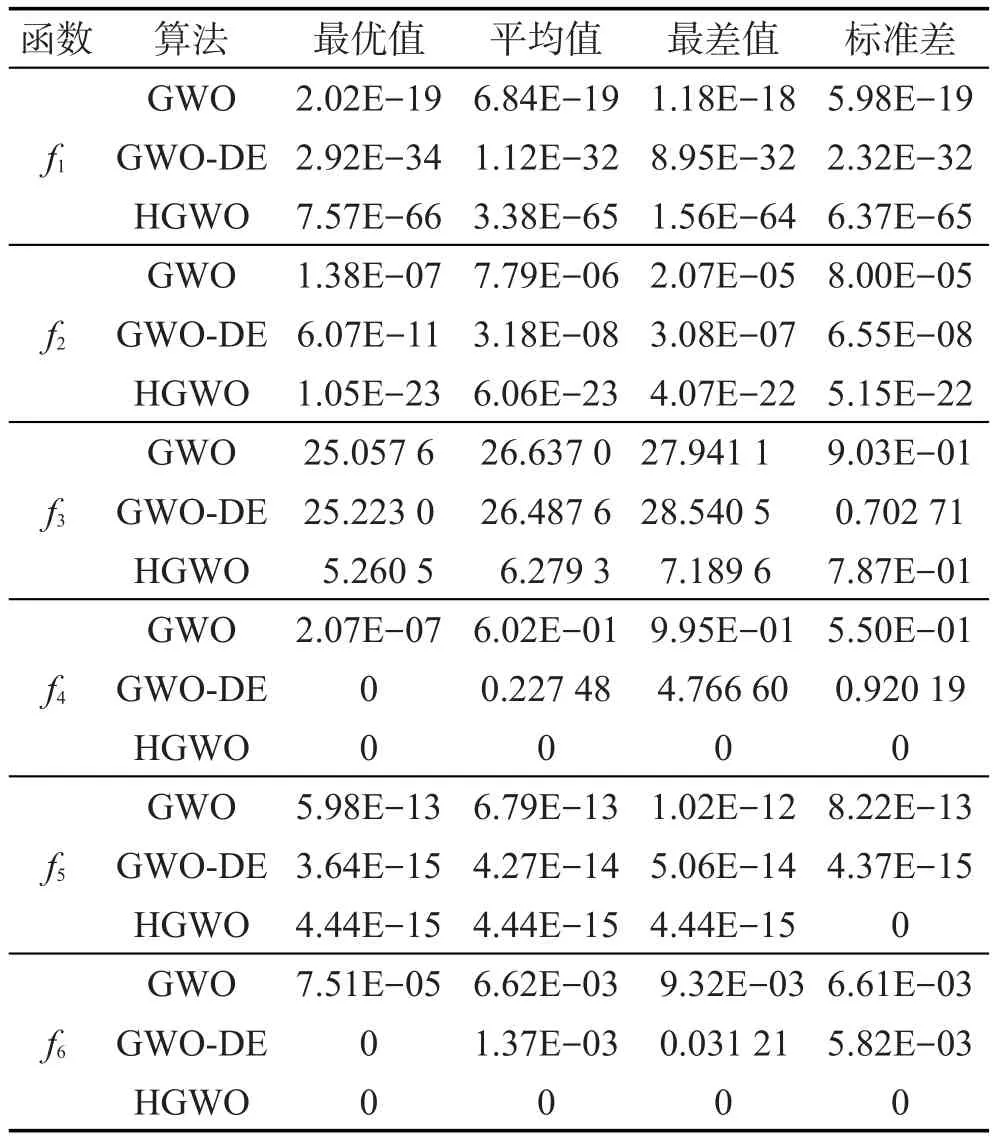
Table 1 Experimental results of 3 algorithms for 6 test functions表1 3种算法对6个测试函数的结果比较

从表1可知，在满足固定收敛精度下，除了Rosenbrock函数，本文提出的HGWO算法在其他5个函数上进行30次实验中均能一致收敛到问题的全局最优解，尤其是Rastrigin函数和Griewank函数，HGWO算法能收敛到理论最优值。对于Rosenbrock函数，3种GWO算法的寻优结果不理想，原因在于Rosenbrock是一个典型的非凸函数，在维数大于3的情况下呈现出多峰特性，其全局极小值位于一条平滑而狭长的抛物线形状的山谷底部，且为优化算法提供的信息很少，因此找到全局极小值就显得相当困难。对于Sphere函数、Schwefel 1.2函数、Rastrigin函数、Ackley函数和Griewank函数，HGWO算法寻优成功率为100%。标准GWO算法对于Sphere函数和Ackley函数，30次实验均能一致收敛到全局最优解，寻优成功率为100%；对于Schwefel 1.2函数和Rastrigin函数，GWO算法能收敛到问题的全局最优解，寻优成功率分别为75%和20%；对于Griewank函数，GWO算法找到的解接近全局最优解。由上述比较得知，与标准GWO算法相比，不论是收敛精度，还是收敛稳定性方面，HGWO算法的寻优性能有了明显的提高。

与GWO-DE算法相比，对于测试函数f1、f2和f3，HGWO算法获得了较好的寻优结果。对于测试函数f4和f6，两种算法得到了相似的最优值0，而HGWO算法获得了较好的平均值、最差值和标准差。对测试函数f5，两种算法取得了相似的结果。

另外，在算法收敛（达到收敛精度1E-06）时间方面，标准GWO算法对6个测试函数30次实验的平均收敛时间分别为6.02 s、60.16 s、27.84 s、26.67 s、7.99 s和23.56 s，而HGWO算法对6个测试函数30次实验的平均收敛时间分别为0.90 s、15.13 s、27.35 s、5.28 s、1.20 s和4.66 s。从平均收敛时间来看，与标准GWO算法相比，HGWO算法的收敛速度明显加快。图2给出了GWO算法和HGWO算法对6个函数的寻优收敛曲线。从图2可以清晰地看出，对于6个函数，HGWO算法均能比GWO算法具有较快的收敛速度。

4.3 与其他进化算法的比较

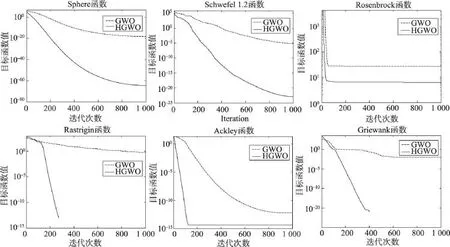
Fig.2 Evolution curves for 6 test functions图2 6个测试函数的进化曲线

为了更进一步验证HGWO算法的有效性，将其与PSO算法[4]、GSA算法[4]和DE算法[4]的结果进行比较。3种算法的参数设置如下：种群规模和最大迭代次数均与HGWO算法设置相同；在PSO算法中，最大惯性权重为0.9，最小惯性权重为0.2，c1=c2=2；在DE算法中，缩放因子F=0.5，交叉概率Pc=0.2；在GSA算法中，G0=100，α=20。为了增加其可信度，PSO、GSA和DE算法的结果直接来源于各自参考文献，结果如表2所示。

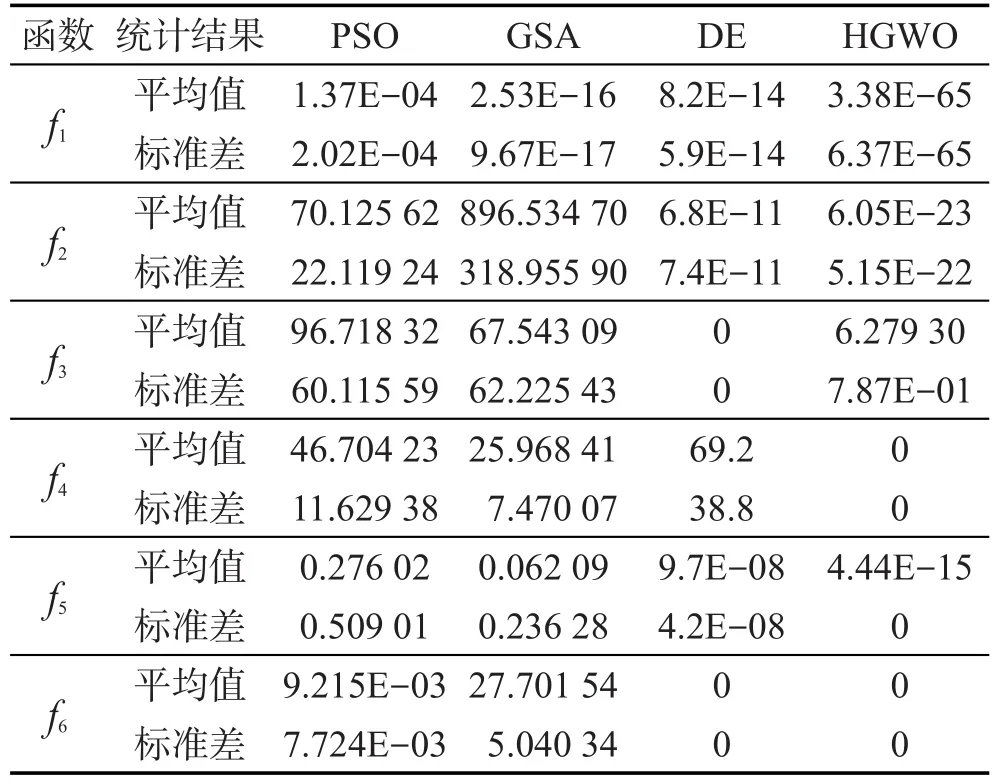
Table 2 Experimental results of 4 different evolutionary algorithms for 6 test functions表2 4种进化算法对6个测试函数的结果比较

从表2可知，与PSO算法和GSA算法相比，HGWO算法在6个函数上均获得了较好的寻优结果。与DE算法相比，HGWO算法在Sphere、Schwefel 1.2、Rastrigin和Ackley函数上获得了较好的结果，在Rosenbrock函数上获得了较差的寻优结果，在Griewank函数上得到了相似的结果。

4.4 对立学习种群初始化的算法性能分析

由3.1节可知，最优保存策略是将上一代种群中的优良个体保存到下一代种群；若初始种群中的优良个体较少，则会直接影响算法的收敛。随机初始化则不能保证初始种群中含有较多的优良个体，因此本文采用对立学习策略来初始化种群个体。下面通过对6个测试函数进行实验，分析采用对立学习策略和随机初始化对算法性能的影响。表3是分别采用两种初始化方法的寻优结果比较。

从表3中结果可知，除了测试函数f6，采用对立学习策略初始化种群方法在其他5个函数上获得的结果明显优于采用随机初始化方法；对于测试函数f6，两种初始化方法取得了相似的寻优结果。从比较结果可以看出，与随机初始化方法相比，采用对立学习初始化种群方法在收敛速度和收敛精度上均有较明显的优势。

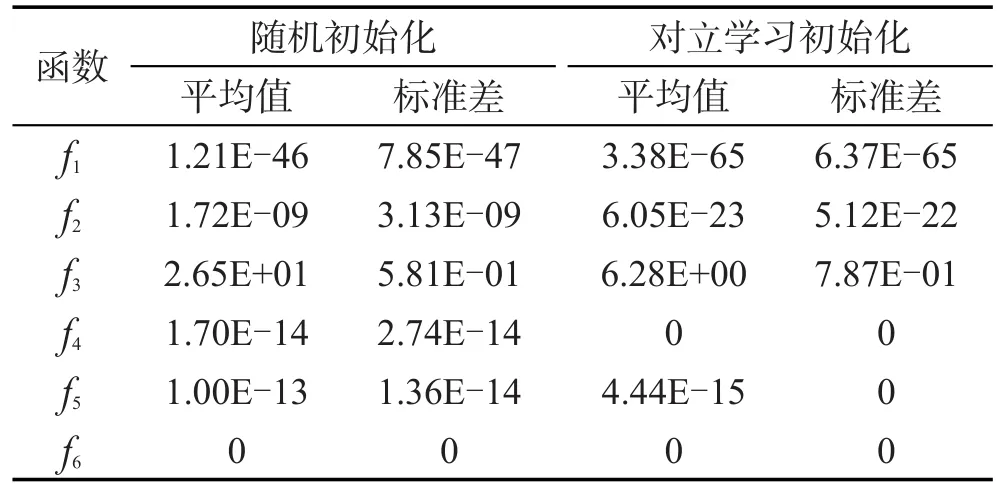
Table 3 Experimental results of 2 initialization methods for 6 test functions表3 两种初始化方法对6个测试函数的结果比较

5 结束语

本文将灰狼优化算法、对立学习策略与Rosenbrock搜索方法相结合，提出了一种混合灰狼优化（HGWO）算法。对6个基准函数进行测试实验，结果表明，相对于其他几种群体智能优化算法，HGWO算法具有寻优精度高，收敛速度快，鲁棒性强等特点。然而，HGWO算法对单峰Rosenbrock函数优化时收敛速度较慢。对HGWO算法进行改进以加强其寻优能力是进一步研究的课题。另外，将HGWO算法用于处理约束优化问题也有待进一步研究。

[1]Akbari R,Ziarati K.A rank based particle swarm optimization algorithm with dynamic adaptation[J].Journal of Computational and Applied Mathematics,2011,235(8):2694-2714.

[2]Seckiner S U,Eroglu Y,Emrullah M,et al.Ant colony optimization for continuous functions by using novel pheromone updating[J].Applied Mathematics and Computation, 2013,219(9):4163-4175.

[3]Tang Lingyun,Mao Li,Zhou Changxi.Improved artificial bee colony algorithm for function optimization[J].Journal of Frontiers of Computer Science and Technology,2015,9(7):854-860.

[4]Mirjalili S,Mirjalili S M,Lewis A.Grey wolf optimization [J].Advances in Engineering Software,2014,69:46-61.

[5]Ei-Gaafary A A M,Mohamed Y S,Hemeida A M,et al. Grey wolf optimization for multi input multi output system [J].Universal Journal of Communications and Networks, 2015,3(1):1-6.

[6]Mirjalili S.How effective is the grey wolf optimizer in training multilayer perceptrons[J].Applied Intelligence,2015, 42(4):608-619.

[7]Madadi A,Motlagh M M.Optimal control of DC motor using grey wolf optimizer algorithm[J].Technical Journal of Engineering andApplied Science,2014,4(4):373-379.

[8]Song H M,Sulaiman M H,Mohamed M R.An application of grey wolf optimizer for solving combined economic emission dispatch problems[J].International Review on Modelling and Simulation,2014,7(5):838-844.

[9]Emary E,Zawbaa H M,Grosan C,et al.Feature subset selection approach by gray-wolf optimization[C]//Advances in Intelligent Systems and Computing 334:Proceedings of the 1st International Afro-European Conference for Industrial Advancement,Addis Ababa,Ethiopia,Nov 17-19,2014. Berlin,Heidelberg:Springer,2014:1-13.

[10]Saremi S,Mirjalili S Z,Mirjalili S M.Evolutionary population dynamics and grey wolf optimizer[J].Neural Computing &Applications,2015,26(5):983-989.

[11]Muangkote N,Sunat K,Chiewchanwattana S.An improved grey wolf optimizer for training q-Gaussian radial basis functional-link nets[C]//Proceedings of the 2014 International Conference on Computer Science and Engineering, Khon Kaen,Thailand,Jul 30-Aug 1,2014.Piscataway, USA:IEEE,2014:209-214.

[12]Zhu Aijun,Xu Chuanpei,Li Zhi,et al.Hybridizing grey wolf optimization with differential evolution for global optimization and test scheduling for 3D stacked SoC[J].Journal of Systems Engineering and Electronics,2015,26(2): 317-328.

[13]Long Wen,Zhao Dongquan,Xu Songjin.Improved grey wolf optimization algorithm for constrained optimization problem[J].Journal of Computer Applications,2015,35(9): 2590-2595.

[14]Tizhoosh H R.Opposition-based learning:a new scheme for machine intelligence[C]//Proceedings of the 2005 International Conference on Computational Intelligence for Modelling,Control and Automation and International Conference on Intelligent Agents,Web Technologies and Internet Commerce,Vienna,Austria,Nov 28-30,2005.Washington:IEEE Computer Society,2005:695-701.

[15]Jia Shujin,Du Bin.Hybrid optimized algorithms based on the Rosenbrock search method and dynamic inertia weight PSO[J].Control and Decision,2011,26(7):1060-1064.

附中文参考文献：

[3]唐凌芸,毛力,周长喜.求解函数优化问题的改进人工蜂群算法[J].计算机科学与探索,2015,9(7):854-860.

[13]龙文,赵东泉,徐松金.求解约束优化问题的改进灰狼优化算法[J].计算机应用,2015,35(9):2590-2595.

[15]贾树晋,杜斌.Rosenbrock搜索与动态惯性权重粒子群混合优化算法[J].控制与决策,2011,26(7):1060-1064.

WANG Min was born in 1978.He is an associate professor at Hunan Mechanical&Electrical Polytechnic.His research interests include intelligent optimization algorithm and evolutionary computation,etc.

王敏（1978—），男，湖南长沙人，硕士，湖南机电职业技术学院副教授，主要研究领域为智能优化算法，进化计算等。

TANG Mingzhu was born in 1983.He received the Ph.D.degree in control science and engineering from Central South university in 2011.Now he is a lecturer at Changsha University of Science&Engineering.His research interests include intelligent optimization algorithm and system simulation,etc.

唐明珠（1983—），男，湖南岳阳人，2011年于中南大学控制科学与工程专业获得博士学位，现为长沙理工大学讲师，主要研究领域为智能优化算法，系统仿真等。

Hybrid Grey Wolf OptimizationAlgorithm with Opposition-Based Learning*

WANG Min1,2+,TANG Mingzhu3
1.Department of Information Engineering,Hunan Mechanical&Electrical Polytechnic,Changsha 410151,China
2.School of Computer and Communication,Hunan University,Changsha 410082,China
3.School of Energy and Power Engineering,Changsha University of Science&Technology,Changsha 410114,China
+Corresponding author:E-mail:wangmin_7819@163.com

The standard grey wolf optimization(GWO)algorithm has a few disadvantages of slow convergence, low solving precision and high possibility of being trapped in local optimum.To overcome these disadvantages of GWO algorithm,this paper proposes a hybrid GWO(HGWO)algorithm based on opposition-based learning strategy and Rosenbrock local search method.In the proposed hybrid algorithm,opposition-based learning strategy is introduced to generate initial population,which strengthens the diversity of population.Rosenbrock local search method is applied to the current best individual,which improves the convergence speed and local search ability of GWO algorithm.Elite opposition-based learning approach is used to avoid premature convergence of GWO algorithm. The experimental results of 6 well-known benchmark functions show that the proposed HGWO algorithm has strong convergence and high precision.

grey wolf optimization algorithm;Rosenbrock search;opposition-based learning

10.3778/j.issn.1673-9418.1509052

A

TP301.6

*The National Natural Science Foundation of China under Grant No.61403046(国家自然科学基金);the Science and Technology Projects of Hunan Province under Grant No.2014FJ3051(湖南省科技计划项目).

Received 2015-09,Accepted 2016-10.

CNKI网络优先出版:2016-10-31,http://www.cnki.net/kcms/detail/11.5602.TP.20161031.1650.004.html

WANG Min,TANG Minzhu.Hybrid grey wolf optimization algorithm with opposition-based learning.Journal of Frontiers of Computer Science and Technology,2017,11(4)：673-680.

摘 要：针对标准灰狼优化（grey wolf optimization，GWO）算法存在后期收敛速度慢，求解精度不高，易出现早熟收敛现象等问题，提出了一种基于对立学习策略和Rosenbrock局部搜索的混合灰狼优化（hybrid GWO，HGWO）算法。该算法首先采用对立学习策略取代随机初始化生成初始种群，以保证群体的多样性；然后对当前群体中最优个体进行Rosenbrock局部搜索，以增强局部搜索能力和加快收敛速度；最后为了避免算法出现早熟收敛现象，利用精英对立学习方法产生精英对立个体。对6个标准测试函数进行仿真实验，并与其他算法进行比较，结果表明，HGWO算法收敛速度快，求解精度高。