四元数小波变换的无参考图像质量评价*

桑庆兵，高 双

江南大学 物联网工程学院，江苏 无锡 214122

四元数小波变换的无参考图像质量评价*

桑庆兵+，高 双

江南大学 物联网工程学院，江苏 无锡 214122

提出了一种新的利用四元数小波变换的通用型无参考图像质量评价算法，其利用四元小波金字塔将二维图像映射到四维空间，每层可以表示为1个幅值和3个相位（Φ，θ，ψ），其中ψ相位包含丰富的图像纹理信息，能有效表征图像的结构信息。因此，通过提取各尺度ψ相位中能有效表征图像失真程度的特征，并构成特征向量，通过支持向量回归（support vector regression，SVR）模型预测图像质量得分。实验结果表明，该算法能有效反映各失真类型图像的视觉感知质量，斯皮尔曼等级相关系数值能达到0.942。

无参考图像质量评价；四元数小波变换；四元小波金字塔；支持向量回归(SVR)

1 引言

图像/视频质量表示图像向设备和人提供信息的能力[1]，是评估图像/视频处理系统或算法性能的重要指标。在实际应用中，往往不能获得原始图像相关信息，大大限制了全参考（full-reference，FR）和半参考（reduced reference，RR）图像质量评价方法的应用。因此，开发一种简单且有效的无参考图像评价算法（no-reference image quality assessment，NR-IQA）尤为重要。

判断图像质量的好坏主要依据图像中边缘和轮廓的判断，纹理作为图像的基本特性，可以有效反映图像的边缘和结构特征变化，在一定程度上表征了图像质量的失真程度。常用的图像纹理分析方法主要有结构法、统计法和模型法。然而，这些方法都是在邻域、单一范围的空间中相互作用的分析，因此往往局限在显微纹理方面的分析，并且采用的单分辨率技术也导致了纹理分析结果不理想。

近年来，小波变换作为新兴的一种多尺度分析方法，主要被应用于基于小波的纹理分类[2]、纹理分析[3]等。虽然传统小波变换在纹理分类中已经取得了显著成果，但仅仅是把指定图像分解为0°、90°、135°的水平、垂直和对角线3个方向上的平滑子带，这就严重制约了小波变换对于旋转不变纹理图像的分析[4]。

由于四元数可以表示2D实值信号，从而相应的基于四元数的小波尺度函数、小波函数的构造就成为解析二维信号的关键。四元数小波变换（quaternion wavelet transform，QWT）理论是实小波、二维希尔伯特变换及四元数代数理论相结合产生的，可以为二维图像提供具体的相位信息。相对于小波变换，QWT克服了实小波变换的两个不足：第一，当信号（图像）微小平移后，图像的边缘区域和平滑的特征会产生很大的变化，造成边缘的模糊；第二，用相位来表示图像的局部信息。双树复小波变换（dual-tree complex wavelet transform，DCWT）虽然很好解决了第一个问题，但它只有一个幅角，在表示二维图像特征时容易出现信号相位歧义。Gabor变换[5]能很好地同时在频域、时域中满足信号对分辨率的要求，成为图像纹理特征提取中最常用的方法，但其计算复杂，一般在提取特征后，还要进行降维处理。QWT具有旋转不变性，并且能对二维信号进行局部幅值和相位分析，计算简单。这些都可以弥补传统小波变换在图像处理中的一些不足。目前国内外已有将QWT应用到图像处理上的研究。文献[6]利用QWT理论提出了一种基于图像多分辨率的视差估计方法。文献[7]充分利用了QWT的旋转不变性、平移不变性进行图像的分析与处理。文献[8]首次将QWT理论应用在图像纹理分类方面，并证明了其方法的可行性。目前把QWT中纹理特征分类与图像质量评价联系起来还没有相关的研究。

本文在上述思想的基础上，综合利弊，将QWT理论与支持向量机（support vector machine，SVM）相结合进行无参考图像质量评价，扩展了QWT理论的应用范围。首先对图像进行四元数小波变换，提取失真图像多个角度和不同尺度的1个幅值和3个相位（Φ，θ，ψ）信息，在考虑图像失真和人类视觉系统的局部性特点基础上，利用ψ相位所蕴含的图像纹理信息，分别在每个尺度提取平均梯度、加权方差、能量，共计27个参数作为纹理特征，把这27个参数作为分类特征，利用支持向量回归（support vector regression，SVR）模型预测图像质量。以下在分析QWT和SVM理论的基础上，详细介绍了本文算法，并通过实验验证了算法的有效性。

2 四元数小波变换的理论基础

2.1 四元数代数

四元数是传统复数概念的推广，是Clifford代数的一个子代数[9]。四元数q可以用式（1）表示如下:

其中，qr、qi、qj、qk均是实数；i、j、k均是虚部单位且满足：

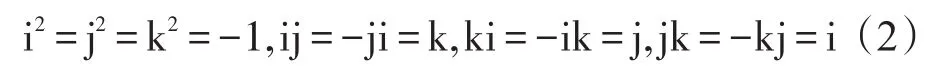
由上可知，Hamilton四元数不符合乘法交换律。四元数q的共轭为q=qr-qii-qjj-qkk。四元数的幅值。

在极坐标下四元数q可以表示为：q=|q|eiΦejψekθ。其中|q|表示四元数的幅值，它具有平移不变性，(Φ，θ，ψ)是四元数的3个相位角[10]，取值范围为：

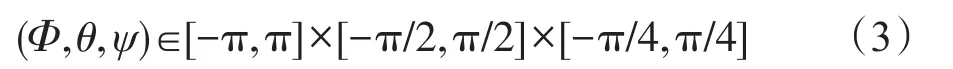
2.2 四元数小波变换

定义1[11]令 f是一个实二维信号。二维四元数解析信号定义为：

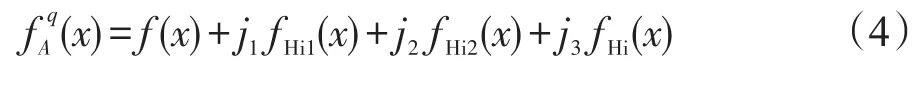
其中：

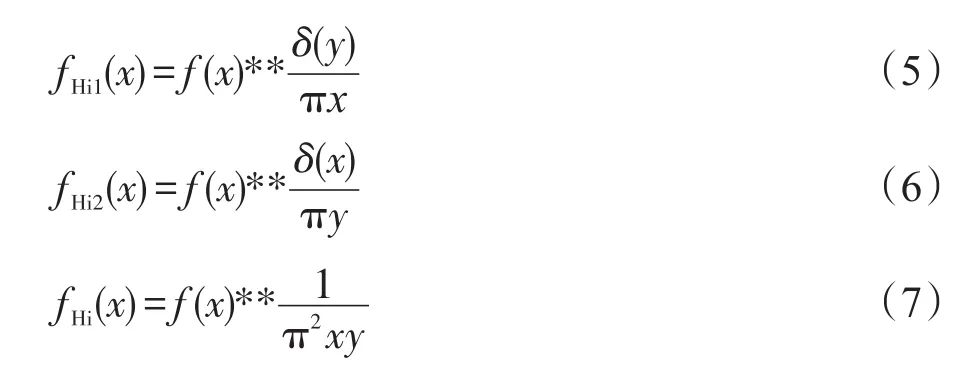
函数 fHi1和函数 fHi2是 f(x)的部分Hilbert变换函数；δ(x)和δ(y)是分别沿二维坐标轴的脉冲函数；**是二维卷积操作。QWT的4个标准正交基用矩阵形式可表示为：

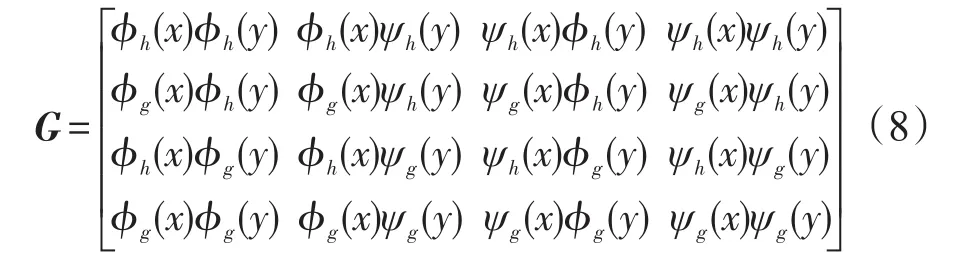
其中每一行表示QWT的一路独立小波，每一列表示其变换的一个子带。如下是对角子带的表示形式：

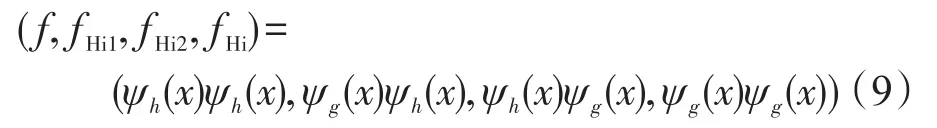
利用四元数代数，可以将4个组分组成为一个四元数小波函数[10]，即：

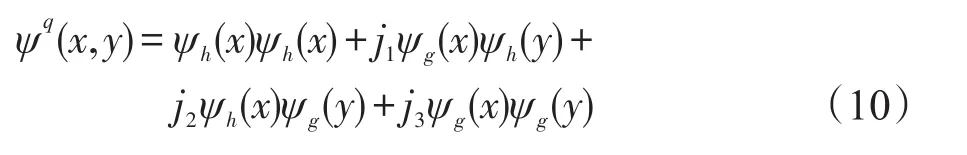
四元数的相位角（Φ，θ，ψ）的具体计算可参考文献[10]。如图1所示给出一个三级四元数小波变换的例子。从图中可以看出ψ相位包含图像的纹理信息，Φ、θ相位编码图像结构的空间位置信息，在一些文献中Φ、θ相位被用来做视差估计。由于ψ相位可以很好地反映图的纹理结构信息[12]，本文选用其相位信息预测图像质量。

3 基于四元数小波变换的相位特征提取

四元数小波变换（QWT）有非常丰富的多尺度空间分析能力，因此QWT在二维信号的幅值和相位信息特征提取方面具有独特优势。每个子带任何位置的特征都可以用幅值表示，同时相位提供了局部特征。随着更多表征图像纹理信息的特征被选取，QWT在某种程度上为SVR分类提供了一个良好的基础。为了能准确有效地度量图像的失真程度，通过QWT选取平均梯度、加权方差和能量来提取图像特征。

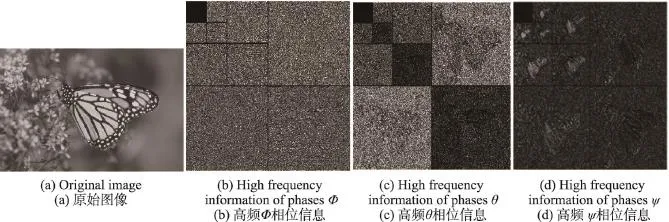
Fig.1 Result of image three level quaternion wavelet transform图1 图像三级四元数小波变换实验结果

3.1 平均梯度

平均梯度能有效反映图像的清晰度。它通过一阶差分来获取该像素点和其相邻像素之间的差异程度，其变化的快慢反映了图像细节信息上反差的大小，最终决定了图像的清晰度。在一定程度上它还能反映出图像的纹理变换特征。平均梯度计算公式为：

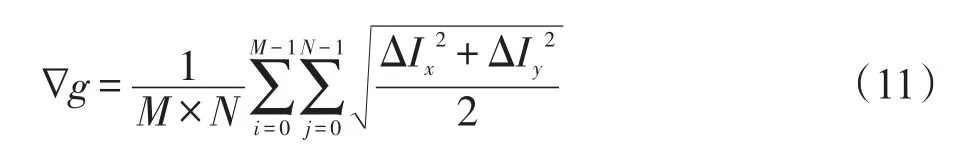
其中，ΔIx与ΔIy分别为沿坐标轴x与y方向上的一阶差分。四元数小波分解中的高频信息ψ相位包含表征图像的局部纹理特征，文中用平均梯度来度量局部纹理特征。

3.2 加权标准偏差

标准偏差在四元数小波中表示相位的相对分布态势，为了使标准偏差更能反映图像的特征，本文对标准偏差进行加权。一个高的幅度值意味着一个显著的图像特征，然而一个低的幅度值意味着没有特征或者是不重要的特征，幅度值很好地展现了其关注显著性特征性质，因而使测量更具有代表性。定义权重函数W是该子带QWT低频系数归一化的值，它和标准偏差结合的公式如下：

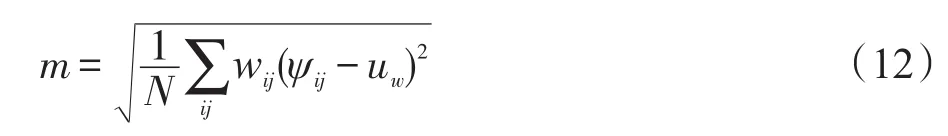
式中，uw=∑ijwijψij是权重均值；N是子带系数中像素的个数；i、j分别为图像像素点的离散坐标，若图像的原始尺寸为M×N，则1≤i≤M,1≤j≤N。

3.3 能量

图像锐利度是图像的一种重要视觉感知度量，它可以通过小波变换后的子带能量进行计算，可以有效反映图像包含信息的丰富程度。本文通过四元数小波变换，提取小波分解各个方向ψ相位的对数能量来计算图像的锐利度。具体公式如下：

式中，E为各子带能量矩阵；T为子带中元素个数；C为相应子带的系数矩阵；s表示分解的尺度数；o是各尺度上的方向数。本文在计算时只选用各尺度ψ方向上的系数，为保证计算各子带对数能量C时出现接近0的异常数值，Φ为调整因子，本文选为1。i、j为子带系数矩阵中像素点的离散坐标值。为与人类主观视觉相一致，本文选取图像的视觉重要区域作为考察对象，即将一幅图像按内容划分成边缘、纹理和平坦区域3部分。具体步骤如下：

步骤1对图像进行三尺度四元数小波基变换；其次对LH、HL和HH小波子带中包含ψ相位的每一个方向子带，边缘纹理区域由系数绝对值大于该子带绝对值均值1.2倍的系数来确定。

步骤2对边缘纹理区域进行膨胀操作，得到膨胀区域。

步骤3对边缘纹理区域和膨胀区域分配权值1，其他区域分配权值0。

本文选择菱形进行膨胀，半径根据尺度由高到低依次选择2、3、4，获取不同尺度下的视觉关注度区域；最后整个子带的系数由包含加权区域的系数来替代，进而得到整个子带的能量。

4QWT-SVR算法具体步骤

4.1 支持向量机基本原理

支持向量机由Vapnik首先提出，用于模式分类和非线性回归。它在模式分类问题上提供极好的泛化性能，这是其他机器学习方法所不具有的。因此，本文采用支持向量机在回归方面的一种算法ε-SVR，回归方程[13]为：

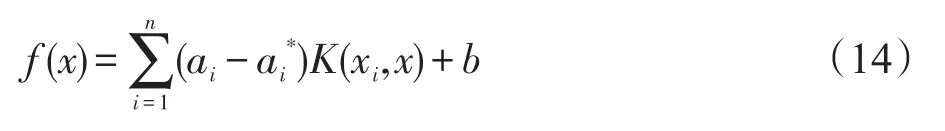
可转化为如下规划问题：

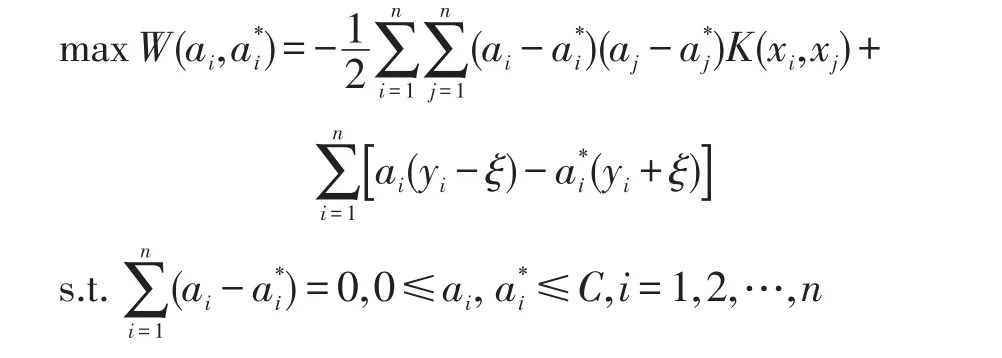
其中，K(xi,x)为核函数。本文采用RBF核函数，因此SVR模型需要预先设定的参数包括惩罚系数、核函数宽度系数和不敏感损失系数ε。

支持向量机预测图像质量的优劣，关键是要找到能有效反映图像失真强度的特征向量。由生物学原理可知，人类视觉系统对图像的纹理结构区域关注度比较高。为此本文先对图像进行四元数小波变换，获取图像的纹理信息，提取平均梯度、加权方差和能量3个特征，最后组成特征向量，输入到ε-SVR模型中来预测图像的质量。

4.2 基于QWT-SVR图像质量评价模型

利用QWT和SVR分类评价图像质量算法如下：

步骤l对待测图像进行三级四元数小波基变换。

步骤2对变换后的系数生成图像幅/相矩阵，提取幅/相矩阵中高频HL、LH和HH子带中相位表示的纹理特征，并组合成一个高维特征向量，输入到SVR模型中进行训练。

步骤3用训练得到的SVR模型预测图像的质量得分。

算法流程如图2所示。

5 实验研究与数据分析

5.1 数据库和性能评价指标

在公开数据库LIVE[14]、CSIQ[15]和TID2008[16]上对本文算法进行测试，数据库中包括图像的失真类型和它们的主观得分DMOS，利用DMOS值可以对图像进行训练和预测，它们的详细特征如表1。

LIVE图像评估数据库有5类失真类型图像（169幅JPEG2000压缩，175幅JPEG压缩，145幅白噪声污染，145幅高斯模糊和145幅快速退化）及29幅无失真原始图像和每幅图像相对应的DMOS值，它的数值在1到100之间变化，数值越小说明图像质量越好。CSIQ数据库有6类失真及30幅原始图像，总共900幅图像。TID2008数据库有25幅原始图像及17种失真类型，共1 700幅图像。将本文算法和BLIINDS-Ⅱ、DIIVINE、NSS-GS和CORNIA无参考图像质量评价算法进行了性能比较。

为了验证本文算法与主观感受的一致性，选用了两个评价准则来度量其性能：（1）反映客观评价算法的准确性的线性相关系数（linear correlation coefficient，LCC），其不受主观评估尺度的影响，取值越接近1，说明算法评价图像质量越精准；（2）反映客观评价算法的单调性的斯皮尔曼等级相关系数（Spearman rank order correlation coefficient，SROCC），取值范围[-1，1]，取值越接近1或-1，表明客观图像质量评价算法单调性越好。

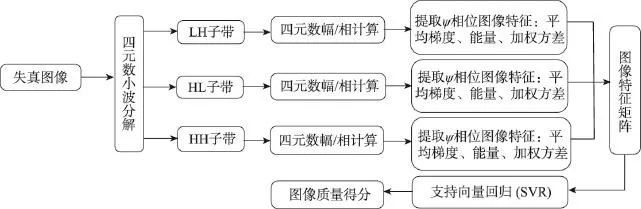
Fig.2 Framework of no-reference image quality assessment based on QWT-SVR图2 基于QWT-SVR的无参考图像质量评价算法框架图

Table 1 Benchmark test databases for IQA表1 IQA的标准测试数据库

5.2 参数设计及仿真实验

在LIVE图像库上，本文按照文献[17]中的方法，随机抽取20%的图片作为测试集，剩余的作为训练集，根据SVR训练模型获得预测值，循环100次，取其中间值作为最后结果。实验中SVR相关参数值设置如下：惩罚系数C由交叉验证算法寻优得到，本文为128；不敏感损失系数ε值设为0.1，径向基核的宽度系数γ取1。

在CSIQ图像评测数据库上，本文排除LIVE图像评估数据库上的快速失真类型和原始参考图像，得到剩余634幅图像作为训练集，根据训练得到的模型，在CSIQ上测试对应4种失真类型（总共600幅）。由于在CSIQ库上缺乏相应的交叉数据库实验数据，选用经典SSIM和PSNR算法做比较。同理，在TID2008数据库上，因为每种失真类型包含4幅人工合成的图像，所以没有包括在内，总共选取384幅图像作为测试集。同样选用LIVE数据库上634幅图像作为训练集，用LIVE数据库的训练模型测试TID2008上图片集的质量。各项实验数据统计如下。

从表2和表3中可以看出，本文算法和同样对5种失真类型评价的BLIINDS-Ⅱ、BIQI相比，各个失真类型都有明显的提高。同样体现了对JPEG评测有待进一步的提高。同基于两部框架的DIIVINE、NSS-GS、NSS-TS相比，各项指标各有优劣，但本文算法不用判断失真类型，计算也更加方便；同较新的基于卷积神经网络（convolutional neutral networks，CNN）的CORNIA算法相比，单个失真类型各有优劣，但在总体测试上具有一定的优势。从图3、图4的100次随机实验的结果可以看出，本文算法可以有效评估各失真类型，尤其在WN、GBLUR、ALL上表现出非常不错的稳定性。从表4～表6、图5和图6可以看出，本文算法在独立数据CSIQ和TID2008上相对其他算法也有一定的优势，进一步反映了本文算法的有效性和推广性。

为了进一步验证本文算法的有效性和健壮性，在LIVE混合失真图像库上对算法进行进一步测试。由于缺乏相应的混合失真对比数据，选用一些比较经典的算法进行比较。方法同上，实验结果和对比如表7和表8所示。

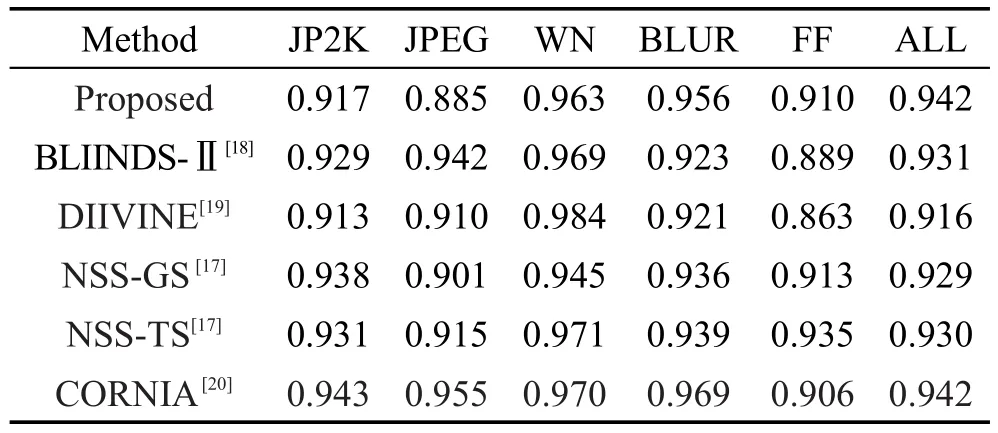
Table 2 Comparison of SROCC on LIVE2 database表2LIVE2数据库上SROCC对比

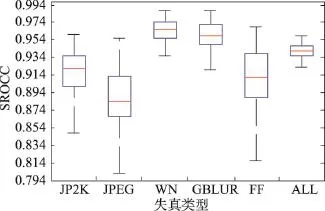
Fig.3 Box plot of SROCC on LIVE2 database图3LIVE2数据库上SROCC箱线图

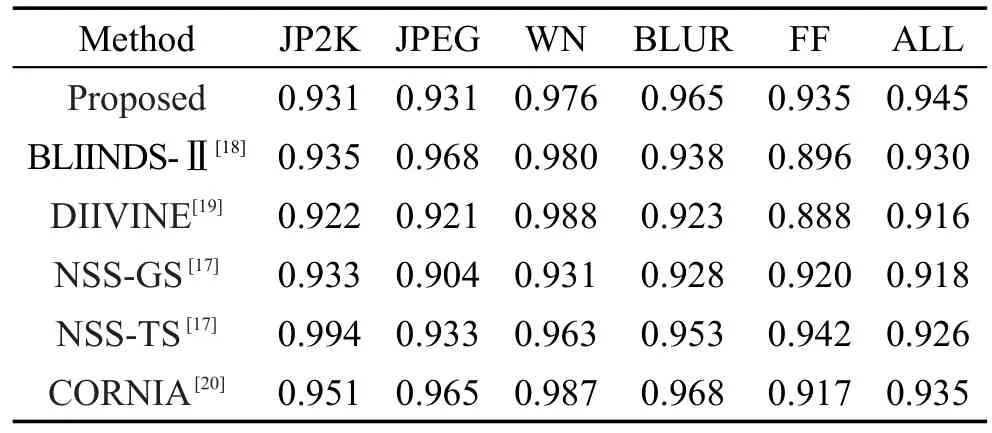
Table 3 Comparison of LCC on LIVE2 database表3LIVE2数据库上LCC对比

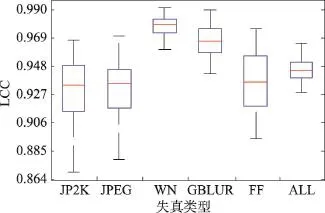
Fig.4 Box plot of LCC on LIVE2 database图4LIVE2数据库上LCC箱线图

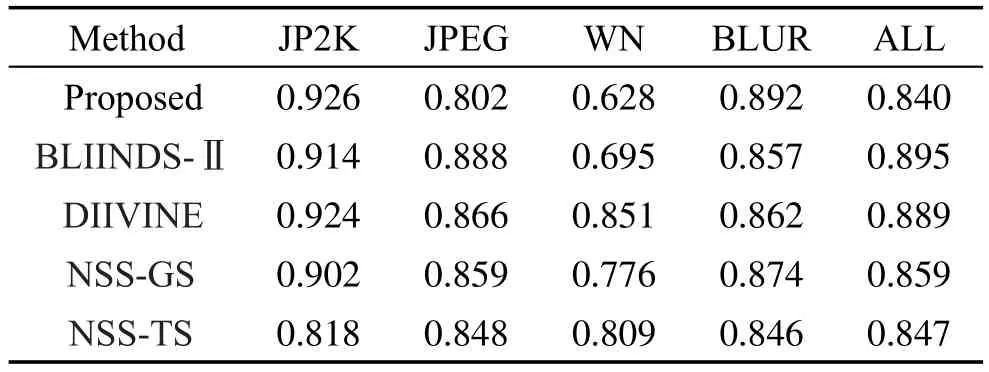
Table 4 Comparison of SROCC on TID2008 database表4TID2008数据库上SROCC对比

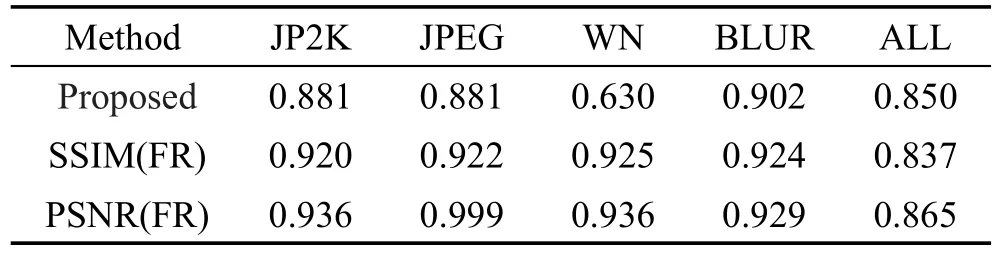
Table 5 Comparison of SROCC on CSIQ database表5CSIQ数据库上SROCC对比

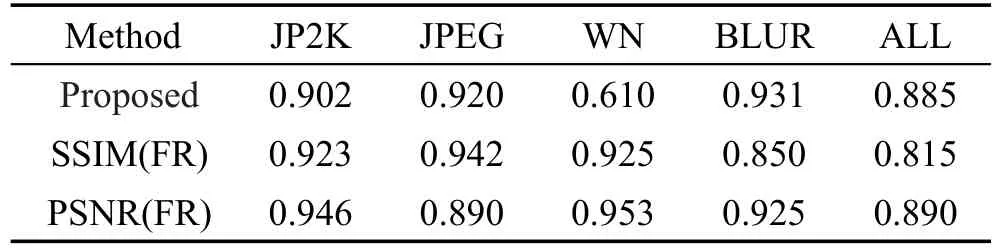
Table 6 Comparison of LCC on CSIQ database表6CSIQ数据库上LCC对比

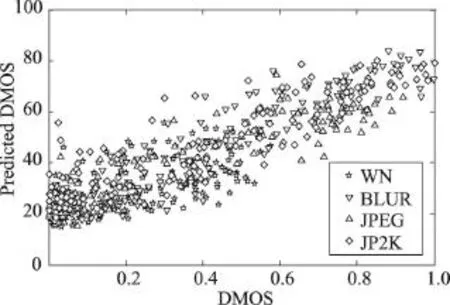
Fig.5 Result of CSIQ tested by LIVE model图5LIVE模型测CSIQ散点图

从表7、表8可以看出，本文算法相对传统算法也具有非常明显的优势，所提取的特征能较好地反映图像失真变化规律，对各种失真类型都能有效度量图像质量。从以上对比实验结果可见，无论在混合失真集或者多种混合失真图像集上，本文算法都能取得较高的算法指标。

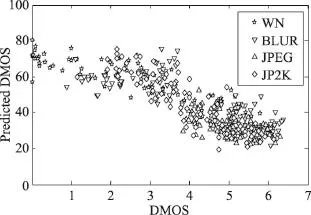
Fig.6 Result of TID2008 tested by LIVE model图6 LIVE模型测TID2008散点图

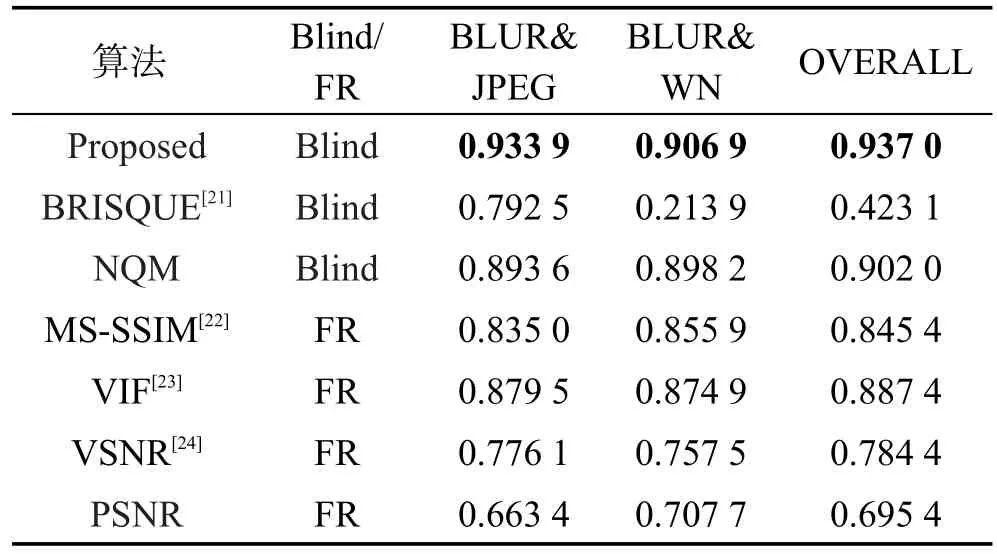
Table 7 Comparison of SROCC for different assessing methods on multi-kind distortion LIVE database表7 不同评价方法在LIVE混合失真图像库上SROCC对比

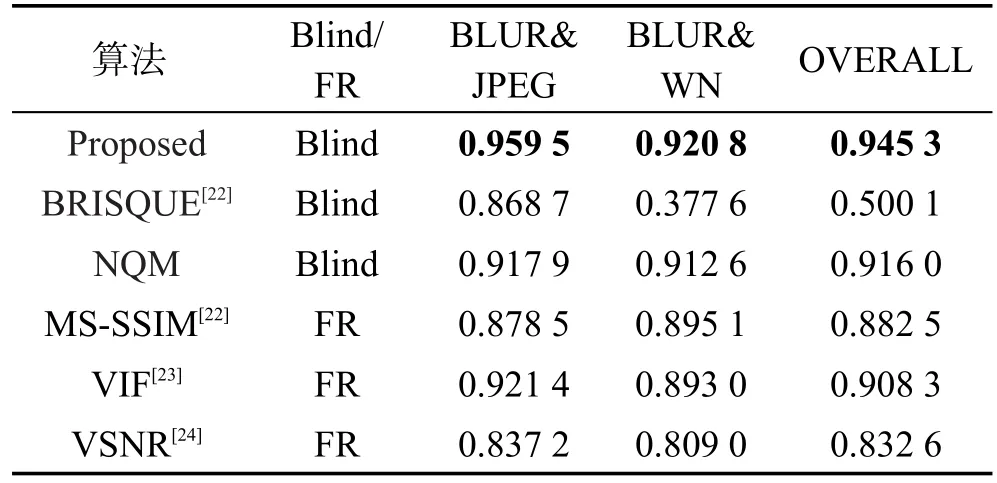
Table 8 Comparison of LCC for different assessing methods on multi-kind distortion LIVE database表8 不同评价方法在LIVE混合失真图像库上LCC对比

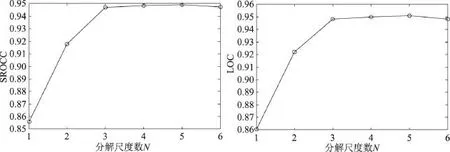
Fig.7 Result of image quality assessment on LIVE database and different N图7 参数N变化在LIVE图像库上的图像质量评价结果

综上所述，本文算法能准确地将图像质量与人类主观感建立起很好的相关度，具有较好的推广性和主客观一致性。

5.3 参数对实验结果的影响

影响本文算法的参数还有求图像特征矩阵时QWT的分解尺度数N，通常情况下研究人员取尺度3，但没有定量分析这个参数对实验结果的影响。为了增加算法的普适性，本文通过实验来定量研究分解尺度数N对实验结果的影响。实验结果如图7所示。

很明显，随着QWT分级尺度的增加，图像质量的度量越精确，分解层数N对图像质量的度量有较大影响，并且随着分解尺度的增加逐渐趋于稳定，有一个获得最佳值的取值范围。对图7的分析可知，最佳的取值范围在3、4、5、6，且彼此差距幅度很小，考虑到算法运行的效率，取尺度数3，这从另一方面证明了本文特征选取也具有普适性。尺度N对算法影响的关键原因在于ψ相位包含图像的相位信息，随着分解尺度数的增加，可以得到更多记录图像边缘改变的高频信息，因此更能精确描述图像质量的变化程度，这也与实验结果分析相一致。

5.4 算法时间复杂度分析

在图像质量评价过程中，提取特征过程所需的计算时间往往要远大于对其进行分类和预测的过程，后者的时间复杂度往往也只与特征维数和机器学习方式有关。本文主要对算法中特征提取时间进行分析。在CPU 3.4 GHz，Core 4，RAM 4配置环境下，对LIVE图像库中的自然图像parrots.bmp进行特征提取，对所需的时间进行比较，结果如表9所示。可以看出QWT-SVR所用的时间复杂度要远低于DIIVINE和BLIINDS-Ⅱ算法。

Table 9 Comparison of time for feature extraction of 3 NR-IQAalgorithms表9 3类无参考特征提取方法所需时间对比

6 结束语

本文介绍了四元数小波变换理论以及它在图像处理中的应用，通过将四元数小波幅值相位特征的提取与SVR算法相结合，提出了一种基于QWT-SVR的无参考图像质量评价算法。本文算法既考虑到图像的多分辨特性，也考虑到图像的内容和视觉感知特性，从整体上反应了IQA的主客观一致性，获得了非常不错的图像质量评价效果。探讨基于小波域统计模型以及与多核学习、深度学习相结合的评价方法，是今后研究的主要工作。

[1]Li Ying,Wang Bo,Kong Xiangwei,et al.Image tampering detection using no-reference image quality metrics[J].Journal of Harbin Institute of Technology,2014,21(6):51-56．

[2]Unser M.Texture classification and segmentation using wavelet frames[J].IEEE Transactions on Image Processing,1995,4(11):1549-1560．

[3]Mallat S G.A theory for multi-resolution signal decomposition: the wavelet representation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1989,11(7):674-693．

[4]Arivazhagan S,Ganesan L,Padam P S.Texture classification using Gabor wavelets based rotation invariant features [J].Pattern Recognition Letters,2006,27(16):1976-1982．

[5]Corner B R,Narayanan R M,Reichenbach S E.Noise estimation in remote sensing imagery using data masking[J]. International Journal of Remote Sensing,2003,24(4):689-702.

[6]Liu Lianhua,Ding Wanshan.Application of quaternion wavelet transform in image processing[J].Electronic Science&Technology,2010,23(4):89-93．

[7]Chan W L,Choi H，Baraniuk R.Quaternion wavelets for image analysis and processing[C]//Proceedings of the 2004 International Conference on Image Processing,Singapore, Oct 24-27,2004.Piscataway,USA:IEEE,2004:3057-3060.

[8]Soulard R,Carré P.Quaternionic wavelets for texture classification[C]//Proceedings of the 2010 IEEE International Conference on Acoustics Speech and Signal Processing, Dallas,USA,Mar 14-19,2010.Piscataway,USA:IEEE，2010:4134-4137．

[9]Li Hongbo.Algebra of Clifford,geometric calculations and geometric reasoning[J].Advances of Mathematics,2003,32 (4):405-415．

[10]Ulow T B.Hypercomplex spectral signal representations for the processing and analysis of images[D].Kiel,Germany: ChristianAl-brechts University,1999．

[11]Moorthy A K,Bovik A C.A two-step framework for constructing blind image quality indices[J].IEEE Signal Processing Letters,2010,17(5):513-516．

[12]Soulard R,Carré P.Quaternionic Wavelets for Texture Classification[J].Pattern Recognition Letters,2011,32(13):1669-1678．

[13]Kale A,Sundaresan A,Rajagopalan A N,et al.Identification of humans using gait[J].IEEE Transactions on Image Processing,2004,13(9):1163-1173.

[14]Sheikh H R,Wang Zhou,Cormack L,et al.LIVE image quality assessment database release 2[DB/OL].(2007-06-30)[2014-02-26].http://live.ece.utexas.edu/research/quality.

[15]Larson E C,Chandler D M.Categorical image quality (CSIQ)database[EB/OL].(2009)[2014-07-23].http://vision. okstate.edu/csiq.

[16]Ponomarenko N,Lukin V,Zelensky A,et al.TID2008—A database for evaluation of full-reference visual quality assessment metrics[J].Advances of Modern Radioelectronics, 2009,10(1):30-45．

[17]Gao Xinbo,Gao Fei,Tao Dacheng,et al.Universal blind image quality assessment metrics via natural scene statistics and multiple kernel learning[J].IEEE Transactions on Neural Networks and Learning Systems,2013,24(12):2013-2026．

[18]Saad M A,Bovik A C,Charrier C.DCT statistics modelbased blind image quality assessment[C]//Proceedings of the 2011 IEEE International Conference on Image Processing, Brussels,Belgium,Sep 11-14,2011.Washington:IEEE Computer Society,2011:3093-3096．

[19]Moorthy A K,Bovik A C.Blind image quality assessment from natural scene statistics to perceptual quality[J].IEEE Transactions on Image Processing,2011,20(12):3350-3364.

[20]Ye Peng,Kumar J,Kang Le,et al.Unsupervised feature learning framework for no-reference image quality assessment[C]//Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition,Provience,USA, Jun 16-21,2012.Piscataway,USA:IEEE,2012:1098-1105.

[21]Tong Hanghang,Li Mingjing,Zhang Hongjiang,et al.Noreference quality assessment for JPEG2000 compressed images[C]//Proceedings of the 2004 International Conference on Image Processing,Singapore,Oct 24-27,2004.Piscataway,USA:IEEE,2004,5:3539-3942．

[22]Zhou Wang,Simoncelli E P,Bovik A C.Multi-scale structural similarity for image quality assessment[C]//Proceedings of the 37th IEEE Asilomar Conference on Signals,Systems and Computers,Pacific Grove,USA,Nov 9-12,2003. Piscataway,USA:IEEE,2003:1398-1402.

[23]Sheikh H R,Bovik A C,Veciana G D.An information fidelity criterion for image quality assessment using natural scene statistics[J].IEEE Transactions on Image Processing,2005, 14(12):2117-2128．

[24]Chandler D M,Hemami S S.A wavelet-based visual signalto-noise ratio for natural images[J].IEEE Transactions on Image Processing,2007,16(9):2284-2298．

附中文参考文献：

[6]柳莲花,丁万山.四元数小波变换在图像处理中的应用[J].电子科技,2010,23(4):89-93．

[9]李洪波.Clifford代数,几何计算和几何推理[J].数学进展,2003,32(4):405-415．

SANG Qingbing was born in 1973.He received the Ph.D.degree in image processing from Jiangnan University in 2013.Now he is an associate professor and M.S.supervisor at Jiangnan University.His research interests include image quality assessment and pattern recognition,etc.

桑庆兵（1973—），男，安徽明光人，2013年于江南大学图像处理专业获得博士学位，现为江南大学物联网工程学院副教授、硕士生导师，主要研究领域为图像质量评价，模式识别等。

GAO Shuang was born in 1987.He is an M.S.candidate at School of Internet of Things Engineering,Jiangnan University.His research interest is image quality assessment.

高双（1987—），男，河南南阳人，江南大学物联网工程学院硕士研究生，主要研究领域为图像质量评价。

No-Reference Image QualityAssessment via Quaternion Wavelet Transform*

SANG Qingbing+,GAO Shuang
School of Internet of Things Engineering,Jiangnan University,Wuxi,Jiangsu 214122,China
+Corresponding author:E-mail:sangqb@163.com

This paper proposes a new general purpose no-reference image quality assessment based on quaternion wavelet transform.It projects a two-dimenisonal image to four-dimenisonal space by using the quaternion wavelet pyramid.Each level of pyramid provides a shift-invariant magnitude and 3-angle(Φ,θ,ψ)phase.Phase ψ includes image texture information and can effectively characterize the structural information of the image.So the method extracts the features which can reflect the degree of image distortion and constitute the feature vector.Finally,the extracted feature is inputted to the support vector regression(SVR)model to predict image quality score.The experimental results show that the proposed algorithm can effectively reflect the visual quality of the image in different distortion types.Spearman correlation coefficient(SROCC)value can reach 0.942.

no-reference image quality assessment;quaternion wavelet transform;quaternion wavelet pyramid;support vector regression(SVR)

10.3778/j.issn.1673-9418.1512042

A

TN911

*The National Natural Science Foundation of China under Grant No.61170120(国家自然科学基金);the Prospective Research Project of Jiangsu Province under Grant No.BY2013015-41(江苏省产学研项目).

Received 2015-12,Accepted 2016-03.

CNKI网络优先出版:2016-03-07,http://www.cnki.net/kcms/detail/11.5602.TP.20160307.1710.010.html

SANG Qingbing,GAO Shuang.No-reference image quality assessment via quaternion wavelet transform. Journal of Frontiers of Computer Science and Technology,2017,11(4)：633-642.