类不平衡模糊加权极限学习机算法研究*

于化龙，祁云嵩，杨习贝，左 欣

1.江苏科技大学 计算机科学与工程学院，江苏 镇江 212003

2.东南大学 自动化学院，南京 210096

类不平衡模糊加权极限学习机算法研究*

于化龙1,2+，祁云嵩1，杨习贝1，左 欣1

1.江苏科技大学 计算机科学与工程学院，江苏 镇江 212003

2.东南大学 自动化学院，南京 210096

从理论上分析了样例不平衡分布对极限学习机性能产生危害的原因；在该理论框架下探讨了加权极限学习机在处理此类问题上的有效性及其固有缺陷；引入模糊集的思想，对传统的加权极限学习机进行了改进，并提出了4种用于解决类不平衡问题的模糊加权极限学习机算法；最后通过20个基准的二类不平衡数据集对所提算法的有效性和可行性进行了验证。实验结果表明：较之加权极限学习机及几种传统的不平衡极限学习机算法，提出的算法可明显获得更优的分类性能，并且与模糊加权支持向量机系列算法相比，所提算法通常可获得与之相当的分类性能，但时间开销往往更小。

极限学习机；类不平衡学习；模糊加权；先验分布信息

1 引言

极限学习机（extreme learning machine，ELM）由Huang等人[1]于2006年正式提出，经过近十年的发展，已经成为机器学习领域的研究热点之一。不同于传统的误差反传（back-propagation，BP）算法[2]，ELM通过随机指定隐层参数，并利用最小二乘法求解输出层权重的方式来训练单隐层前馈神经网络（single hidden-layer feedback network，SLFN），故其具有泛化能力强，训练速度快等优点[3-4]。因ELM的上述优点，其已在诸多实际领域中得到了具体应用，包括人脸识别[5]、遥感图像分类[6]、风能模型构建[7]、企业生命周期预测[8]、空气质量检测[9]和生物信息学[10]等。

尽管ELM具有诸多优点，但其也存在一个固有的缺点，即当数据分布极为不平衡时，分类性能往往大幅下降[8-9,11]。实际上，类不平衡问题也是各种传统分类算法所面临的一个共性问题。所谓类不平衡问题，即数据集中的某一类样例远多于另一类，从而导致以整体错分率最小化为训练目标的分类算法失效的问题。针对这一问题，前人已进行了大量的研究，并给出了诸多解决方法，包括样例采样[12-13]、样例加权（也称代价敏感学习）[14]、分类面偏移[15]、一类分类器[16]和集成学习[17-18]等。具体到ELM，Zong等人[11]借鉴代价敏感学习的思想，提出了一种加权极限学习机（weighted extreme learning machine，WELM）算法。该算法通过为不同类的样例赋予不同权重，从而改变其惩罚因子的方式，达到提升少数类样例识别精度的目的，其缺点在于为同类样例分配的权重均相同，并未考虑样例先验分布信息的作用。Vong等人[9]将ELM与随机过采样技术（random oversampling，ROS）相结合，并用于空气质量检测，提升了空气中固体颗粒物等级的识别率。Sun等人[8]则将SMOTE（synthetic minority oversampling technique）算法[12]引入到ELM集成学习的框架中，在企业生命周期的预测任务上获得了很好的性能。

上述工作尽管均围绕ELM分类器提出了相应的不平衡学习算法，但并未在理论上对类不平衡如何危害ELM性能的原因进行分析。故本文拟首先对该问题展开分析，并进一步在该理论框架下对WELM算法的有效性进行讨论。接下来，考虑WELM算法未耦合样例先验分布信息这一缺点，借鉴文献[14]的思想，引入模糊集的概念，分别设计了4种隶属函数，并进一步相应地提出了4种用于解决类不平衡问题的模糊加权极限学习机（fuzzy weighted extreme learning machine，FWELM）算法。通过从Keel数据仓库[19]中随机抽取的20个基准的二类不平衡数据集对上述算法的有效性与可行性进行了验证。实验结果表明：相对于WELM算法及几种传统的类不平衡极限学习机算法，FWELM系列算法可获得明显更优的分类性能。而与模糊加权支持向量机（fuzzy support vector machine for class imbalance learning，FSVM-CIL）系列算法[14]相比，FWELM系列算法通常可获得与之相当的分类性能，但时间开销往往更小。

2 理论分析

2.1 极限学习机

2006年，新加坡南洋理工大学的Huang等人[1]针对SLFN的训练问题，提出了极限学习机理论与算法。不同于传统的BP学习算法[2]，极限学习机无需对网络的权重与偏置进行迭代调整，而是通过最小二乘法直接计算得到，故大大提升了网络的训练速度，并在一定程度上降低了网络陷入过适应的概率。SLFN的基本结构如图1所示。

Fig.1 Basic structure of single-hidden-layer feedforward neural network图1 单隐层前馈网络的基本结构图

众所周知，在监督学习中，学习算法通常采用有限的训练样本来生成学习模型。假设训练样本集包括N个训练样例，则其可表示为(xi,ti)∈Rn×Rm。其中，xi表示n×1维的输入向量，ti表示第i个训练样本的期望输出向量。对于分类问题而言，n代表训练样本的属性数，m则代表样本的类别数。如图1所示，若一个具有L个隐层节点的单隐层前馈神经网络能以零误差拟合上述N个训练样本，则意味着存在βi、ai及bi，使得下式成立：

其中，ai和bi分别表示第i个隐层节点的权重与偏置；βi表示第i个隐层节点的输出权重，即第i个隐层节点到各输出节点的连接权重；G表示激活函数。则式（1）可进一步简化为下式：

其中：

其中，G(ai,bi,xj)表示第j个训练样本在第i个隐层节点上的激活函数值；T为所有训练样本对应的期望输出矩阵，通常将每个样本所对应类别输出节点的期望输出值设为1，其他节点的输出值则设为-1；H被称为隐层输出矩阵，其第i列为第i个隐层节点在所有训练样本上的输出向量，第j行为第j个训练样本在整个隐藏层中对应的输出向量。

在ELM中，由于所有ai和bi均是在[-1,1]区间内随机生成的，故输入样例、隐层权重与偏置、期望输出（类别标记）均已知，则输出权重矩阵β的近似解即可由下式直接计算得到：

其中，H†为隐层输出矩阵的Moore-Penrose广义逆。根据其定义，可推知βˆ为该网络的最小范数最小二乘解。因此，极限学习机可通过一步计算得到，而无需迭代训练，这就保证了神经网络的训练时间能被大幅缩减。同时，由于在求解过程中，约束了输出权重矩阵β的l2范数，使其最小化，故可保证网络具有较强的泛化性能。

2012年，Huang等人[3]又提出了ELM的优化版本，优化式表示如下：

其中，εi表示第i个训练样本的实际输出与期望输出之差；h(xi)为第i个样例xi在隐层上的输出向量；C则为惩罚因子，用于调控网络的泛化性与精确性间的平衡关系。上述优化式可通过求解得到，给定一个具体的样例x，其对应的实际输出向量可由下式求得：

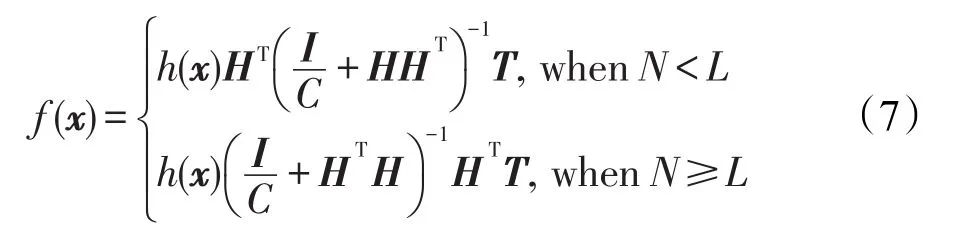
其中，I表示单位矩阵；f(x)=[f1(x),f2(x),…,fm(x)]表示样例x的实际输出向量，并可进一步通过下式确定该样例的预测类标：

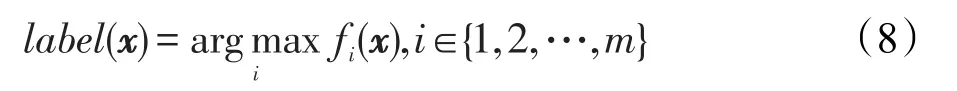
2.2 类不平衡分布对极限学习机性能的影响机理

众所周知，对于ELM而言，那些在特征空间中相邻较近的样例通常会有极其相似的输出值，而在类重叠区域，多数类样例会将少数类样例紧密地包裹其中，它们的输出值极为接近。为同时保证所训练的ELM具有较强的泛化能力与较低的训练误差，少数类必然做出更多的牺牲。不失一般性，假设分类任务只有两个类别，其中在ELM中，少数类对应的期望输出为1，而多数类的期望输出为-1。考虑特征空间中两类样例的重叠区域，从该区域分割出一个足够小且样例分布致密的子区域，在这一区域中多数类样例有S个，而少数类样例数恰好只有1个，即在此区域中，不平衡比率为S，则根据ELM的构造机理，这S+1个样例有极其近似的输出值。设该少数类样例的特征向量为x0=(x01,x02,…,x0n)，则N个多数类样例的特征向量可表示为xi=(x01+Δxi1,x02+Δxi2,…,x0n+ Δxin),i∈{1,2,…,S}，其中，Δxij表示第i个多数类样例与少数类样例x0相比，在第j个特征上的变化量。则在ELM训练完成后，这些样例的实际输出可表示为：

若以Δf(xj)来表示第j个多数类样例对比少数类样例x0在实际输出上的变化量，则其可表示如下：

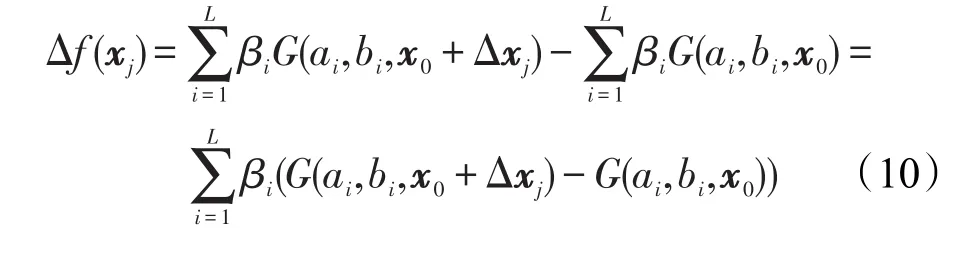
若其中的激活函数G采用的是连续函数，且同时相邻样例在特征空间上的变化量Δxj，隐层权重与偏置的l2范数||a||和||b||，以及输出权重矩阵的l2范数||β||均足够小，可保证两个邻近样例实际输出的变化量Δf(xj)足够小。回顾式（6），假定输出权重矩阵 β已预先确定，则该致密区间的样例子集Qsub的均方训练误差可表示为：

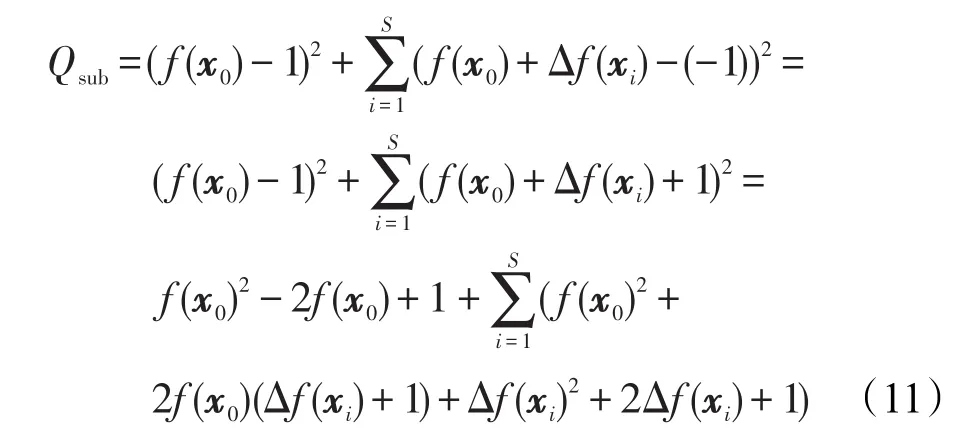
为最小化该子集的均方训练误差，可通过下式求解：

对上式进行求解，可得该子区间内的少数类样例的实际输出为：

2.3 加权极限学习机及其有效性分析

为有效缓解样例不平衡分布对ELM所产生的负面影响，Zong等人[11]借鉴代价敏感学习的思想，提出了一种加权极限学习机算法，即WELM算法。该算法通过为不同类样例赋予不同权重，从而改变惩罚因子的方式，有效降低了少数类样例被错分的概率。在WELM算法中，式（6）被改写为如下形式：

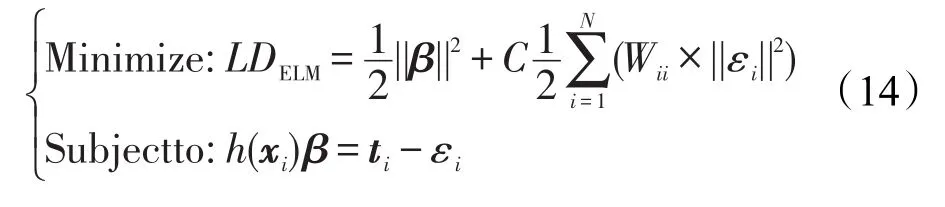
其中，W为一个N×N的对角阵；Wii为第i个训练样例所对应的权重。若对少数类样例施以比多数类样例更大的权重，则会增大对其训练误差的惩罚力度，从而相应降低其被误分的概率。

在文献[11]中，Zong等人提供了如下两种权重分配方法：

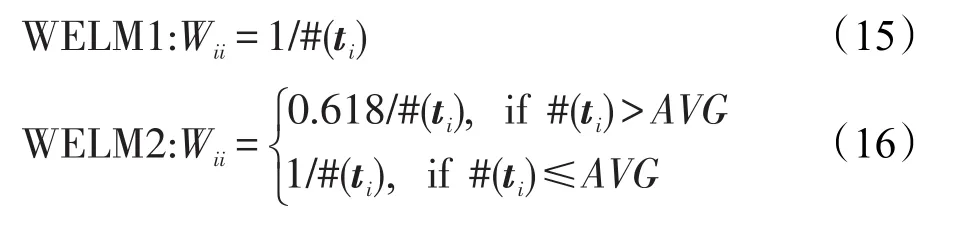
其中，#(ti)和AVG分别代表ti类的训练样例数及所有类的平均训练样例数。显然，无论对于上述哪种权重分配方式，少数类样例都会被赋予更大的权重，且类不平衡比率越高，不同类样例间的权重比也将越高。

接下来，采用2.2节中所提出的理论分析框架，对算法的有效性进行分析。设少数类样例权重为多数类样例权重的M倍，则式（11）可被改写为：

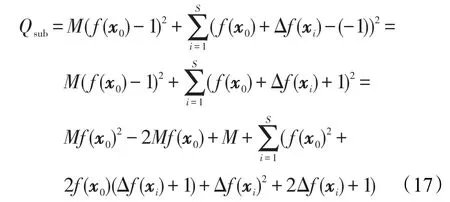
为最小化加权训练误差，可通过以下偏导式求解：

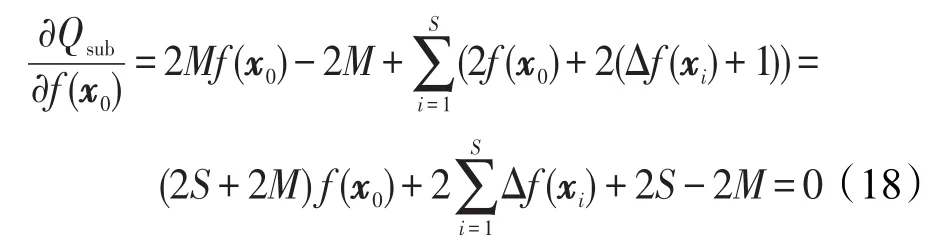
对上式进行求解，可得封闭区间内少数类样例的输出为：

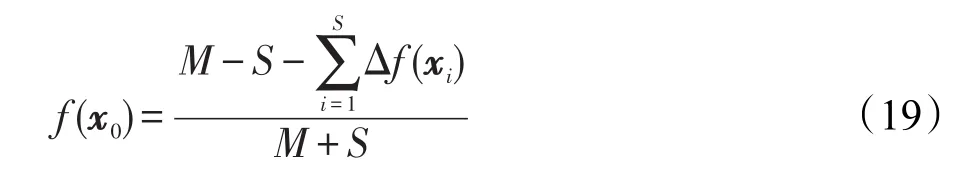
由上式可见，当权重比M与封闭区间内的类不平衡比S十分接近时，该少数类样例将输出一个非常接近于0的值，即表明该样例将出现于所训练的实际分类面附近。显然采用该方法可有效缓解样例不平衡分布对ELM性能所产生的负面影响。

3 本文算法

3.1 基本思想

尽管WELM算法能在一定程度上提升ELM在类不平衡数据上的分类性能，但其仅依照类不平衡比率为每类样例分配一个统一的权重，而没有考虑样例在特征空间中的具体分布情况，故性能往往难以达到最优。且根据文献[14]所述，数据集中往往存在或多或少的噪声样例与离群样例，它们的出现将会进一步影响加权算法的性能。因此，本文拟借鉴文献[14]的思想，引入模糊集的概念，充分挖掘每个样例在特征空间中的分布信息，并对其各自的权重进行模糊化与个性化设置，从而最大化分类性能。

3.2 隶属函数的设计

众所周知，对于一个模糊加权算法而言，影响其性能的最关键因素即是隶属函数设计的合理性，故针对本文所要处理的类不平衡问题，在设计隶属函数时主要应考虑以下两个因素的影响：（1）类不平衡比率；（2）样本在特征空间所处的位置。

首先，考虑类不平衡比率的影响。假设在训练集上的整体类不平衡比率的倒数为r，即少数类与多数类样本数之比为r，则可将两类样本的隶属函数分别写为：

接下来，考虑样本在特征空间的具体分布信息，为不同样本分配合理的评估函数值。借鉴文献[14]的做法，分别以样本距质心距离及样本至分类面距离两个评估标准设计了如下4种评估函数。

（1）基于质心距离的线性衰减评估函数

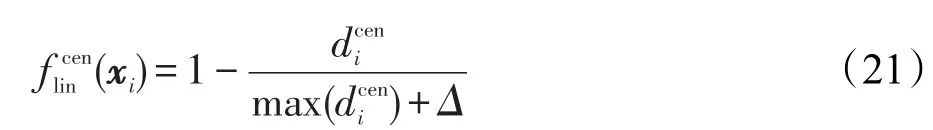
（2）基于质心距离的指数化衰减评估函数

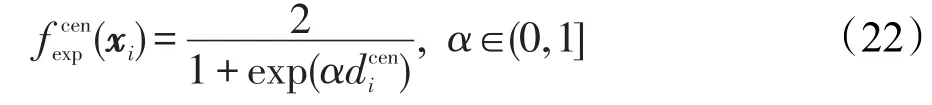
其中，α为调控因子，其取值范围在(0,1]之间，在实际应用中，该参数既可根据经验设定，也可采用内部多折交叉验证法选取。与线性衰减评估函数一样，指数化的衰减评估函数的取值范围也在(0,1]之间，且距质心越远的样本，其被分配的权重也越小。

（3）基于分类面距离的线性衰减评估函数

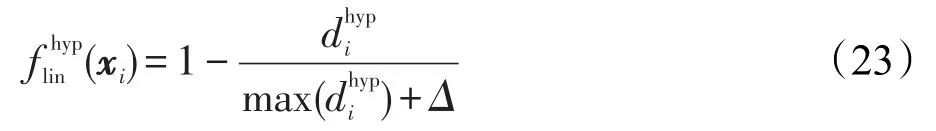
（4）基于分类面距离的指数化衰减评估函数

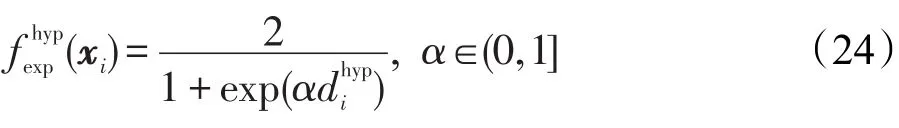
与基于质心距离的指数化衰减评估函数相同，该函数也是将权重测度做了指数化处理，其与前者的唯一区别在于其测试的是样本至初始分类面而非质心的距离。

通过对上述评估函数进行分析，可以看出其优点在于：（1）充分挖掘了训练样本的先验分布信息，并可根据不同样本的重要度对其权重进行个性化的设置；（2）对噪声样本与离群样本赋予了较小的权重，可最大限度降低其对所训练分类器质量的负面影响。综上，可对各类模糊加权准则的隶属函数进行总结，如表1所示。

Table 1 Membership functions of 4 fuzzy weighted rules表1 4种模糊加权准则的隶属函数

在表1中，FWELM-CL表示基于质心距离线性衰减评估函数的模糊加权准则，FWELM-CE表示基于质心距离指数化衰减评估函数的模糊加权准则，FWELM-HL表示基于分类面距离线性衰减评估函数的模糊加权准则，而FWELM-HE则表示基于分类面距离指数化衰减评估函数的模糊加权准则，上述各准则均建立在ELM分类器基础上。

3.3 本文算法描述

采用上一节所提供的4种模糊加权准则，给出了如下两大类共4种模糊加权极限学习机算法的一般性描述。

算法1基于质心距离测度的不平衡模糊加权极限学习机

输入：训练样本集X={(xi,yi)|i=1,2,…,N}，隐层节点数L，惩罚因子C，内部交叉验证的折数E。

输出：所训练的分类器FWELM-C。

步骤1对原始的训练样本集X进行划分，分别得到少数类样本集X+及多数类样本集X-。

步骤2分别计算X+及X-的质心位置，记为cen+及cen-。

步骤3若采用线性衰减评估函数，则计算每个样本xi与其同类质心的欧式距离dceni，从中选出距离两类质心的最远距离，并采用式（21）计算各个样本的评估函数值(xi)，最后采用表1中FWELM-CL所提供的方法计算每个样本的隶属函数值，设置模糊加权矩阵W；若采用指数化的衰减评估函数，则计算每个样本xi与其同类质心的欧式距离dceni，预设调控参数α的取值范围及取值间隔λ，并将训练样本集X随机均分为E折，采用式（22），以内部E折交叉验证的方式确定最优的调控参数值β，最后采用已确定的最优参数α计算训练集X中各个样本的评估函数值(xi)，并进一步采用表1中FWELM-CE所提供的方法计算每个样本的隶属函数值，对模糊加权矩阵W进行设置。

步骤4以L和C作为参数，调用WELM算法[11]训练分类器FWELM-C。

算法2基于分类面距离测度的不平衡模糊加权极限学习机

输入：训练样本集X={(xi,yi)|i=1,2,…,N}，隐层节点数L，惩罚因子C，内部交叉验证的折数E。

输出：所训练的分类器FWELM-H。

步骤1对原始的训练样本集X进行划分，分别得到少数类样本集X+及多数类样本集X-。

步骤2以L和C作为参数，调用原始的ELM算法训练一个分类器。

步骤3若采用线性衰减评估函数，则计算每个样本在所训练分类器上实际输出值的绝对值，将其作为距离测度，并从中找出各类样本至分类超平面的最大距离，进而采用式（23）计算各个样本的评估函数值(xi)，最后采用表1中FWELM-HL所提供的方法计算每个样本的隶属函数值，设置模糊加权矩阵W；若采用指数化的衰减评估函数，则计算每个样本在所训练分类器上实际输出值的绝对值，将其作为距离测度，并预设调控参数α的取值范围及取值间隔λ，将训练样本集X随机均分为E折，采用式（24），以内部E折交叉验证的方式确定最优的调控参数值α，最后采用已确定的最优参数α计算训练集X中各个样本的评估函数值(xi)，并进一步采用表1中FWELM-HE所提供的方法计算每个样本的隶属函数值，对模糊加权矩阵W进行设置。

步骤4以L和C作为参数，调用WELM算法[11]训练分类器FWELM-H。

从上述算法流程可以看出，与传统的WELM算法相比，无论是采用线性衰减评估函数，还是指数化的衰减评估函数，算法的时间复杂度都会有一定幅度的增加。具体到线性衰减评估函数，由于其仅涉及到每个样本与质心间距离的度量以及最大距离的选取，故其在时间复杂度上的增量为O(N)，即其仅与训练样本的规模N有关。而对于指数化的衰减评估函数，由于加入了一个内部交叉验证的参数寻优过程，必然使其时间复杂度大幅增加，具体的增量为O(EN/λ)，即其不但与训练样本数有关，同时也与参数α的调整步长λ及内部交叉验证的折数E密切相关。折数越大，步长越小，则时间复杂度自然也越高。当然，基于“天下没有免费午餐”理论[21]，这些增加的时间开销也有助于帮助人们找到更优的距离测度，从而使分类性能得到进一步提升。

4 实验结果与讨论

4.1 数据集与参数设置

采用从Keel数据仓库[19]中随机选取的20个二类不平衡数据集对本文算法及其比较算法的性能进行了测试。这些数据集具有不同的样例数、特征数与类不平衡比率，具体信息如表2所示。

本文实验的硬件环境为：Intel酷睿i53210M，CPU主频2.2 GHz，内存4 GB，硬盘1 TB；操作系统为Windows 7；编程环境为Matlab2013a。

为展示本文算法的有效性，将其与多个算法进行了实验比较，包括ELM[3]、WELM1[11]、WELM2[11]、RUSELM、ROS-ELM[9]及SMOTE-ELM[8]。同时，为保证比较结果的公正性，本文对不同算法的参数进行了统一设置，其中ELM中隐层节点数L及惩罚因子C均给定了统一的取值范围，采用Grid Search策略确定最优的参数组合，具体取值范围为L∈{20,40,…, 400}，C∈{2-20,2-18,…,220}。此外，考虑到ELM算法具有随机性，故对上述每种算法，其分类结果均以10次外部随机5折交叉验证取均值的方式给出。针对本文算法，其特有的4个参数α、λ、E及Δ参照文献[14]进行设定，即α的取值范围为[0.1,1.0]，取值间隔λ为0.1，内部交叉验证折数E取值为5，Δ的取值为10-6。SMOTE算法中最重要的参数k参照文献[12]将其设置为缺省值5。除整体分类精度Accuracy外，本文也采用类不平衡学习领域中最为常用的两种性能评价测度F-measure和G-mean来比较各类算法的性能，有关这两种性能测度，可参见文献[15]。

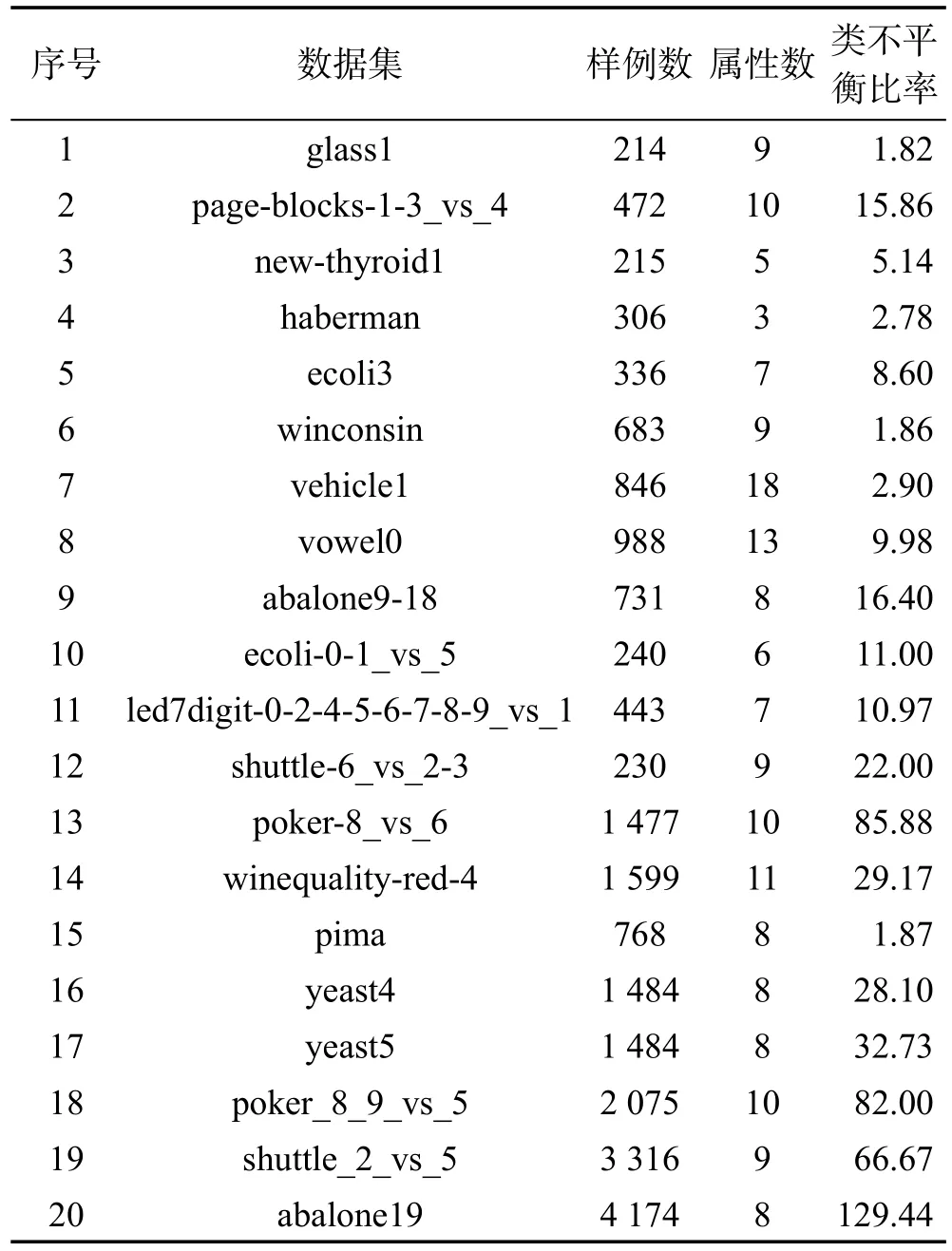
Table 2 Information of used datasets in this paper表2 本文所用数据集信息

4.2 结果与讨论

图2分别展示了各类基于ELM的不平衡学习算法在Accuracy、F-measure及G-mean等3种测度上的实验结果。从该图的比较结果可以得出如下结论：

（1）与传统的ELM算法相比，各种不平衡学习算法不但无助于提升分类的整体精度，而且通常还会导致这一测度值下降。尤其在那些不平衡比率较高的数据集上，其性能下降的幅度还往往较大。事实上，这一现象并不难解释：传统分类器通常是以整体错分率最小为训练目标，而不平衡学习算法则追求不同类样本在分类精度上的平衡，故在正常情况下，前者的精度必然高于后者，这也是在不平衡学习领域为何通常不采用整体分类精度作为性能评价测度的主要原因。

（2）从F-measure和G-mean两种测度上可以看出，在绝大多数不平衡数据集上，无论采用采样技术、传统加权技术还是模糊加权技术，均可有效缓解不平衡分布对分类器性能所产生的负面影响。上述技术与ELM算法相比，在性能上均可得到或多或少的提高。

（3）与随机降采样技术RUS相比，采用过采样技术ROS或SMOTE通常能获得更好的分类性能，尤其在如poker-8_vs_6和abalone19这样的极度不平衡数据集上，这种现象表现得要更为明显。这一现象其实易于解释：因为在极度不平衡的数据集上进行随机降采样，会移除大量包含有重要分类信息的多数类样本，使训练集的绝对样例规模大幅减小，从而导致生成质量较差的分类模型。

（4）与随机过采样技术ROS相比，SMOTE策略并未展现出明显更优的性能，尽管根据前人研究，SMOTE能有效解决ROS易于出现过适应的问题。究其原因，不难发现：ELM具有较强的泛化性能，故其可有效抵制过适应现象的出现[3-4]。

（5）传统加权策略仅能获得与过采样策略大致相当的性能，对两种传统的加权策略进行对比，会发现WELM1往往在G-mean测度上表现得更好，而WELM2在F-measure上则有着明显更为优异的表现。事实上，该现象的出现与二者的权重分配规则有着密切的联系，前者调整得更为激进，而后者则采用了相对温和的调整策略。

（6）在某些数据集上，采用不平衡学习算法不但难以提高分类性能，甚至会造成分类性能的下降，如winconsin数据集。需要从数据分布的角度对这一现象加以解释，因不平衡数据对分类器产生危害的大小是由多因素所决定的，如不平衡比率、不同类样本在特征空间的离散度、训练样本的总规模以及噪声样本的比例等。相信在上述数据集上，两类样本的离散度应该较大，且噪声样本的比例较小，故并未对原始分类器产生性能上的危害。

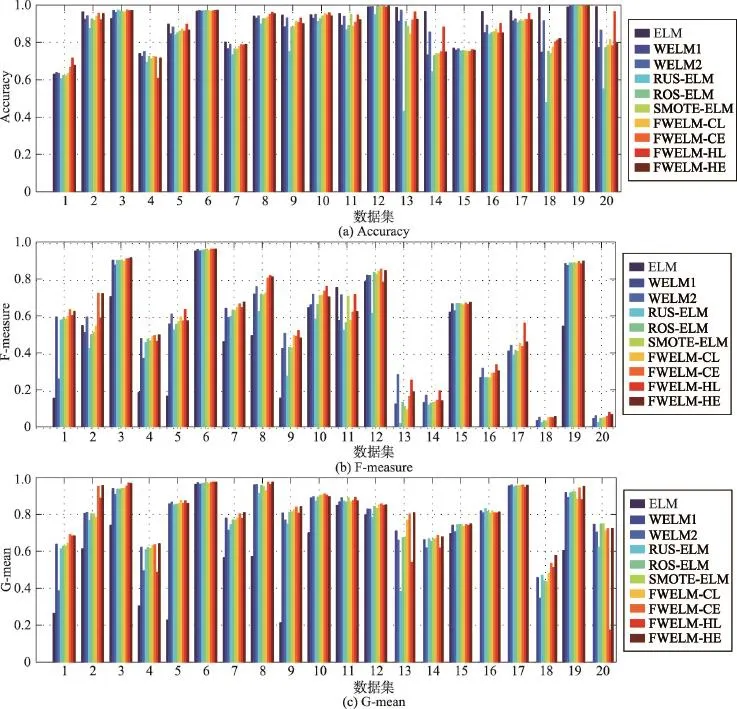
Fig.2 Comparative results of various algorithms onAccuracy,F-measure and G-mean图2 各类算法Accuracy、F-measure及G-mean测度上的实验比较结果

（7）与传统的不平衡学习算法相比，本文所采用的4种模糊加权算法在性能上均有较大幅度的提升，尤其是基于分类面距离测度的两种算法表现得更为优异，其在14个数据集上获得了最高的F-measure值，在12个数据集上获得了最高的G-mean值。由此可见，对处于类重叠区域的样例施以较大的权重更易于获得精细且公正的分类面。

（8）对比两类评估函数，指数化的衰减评估函数表现明显更优。原因在于其通过调整步长来选取最优的距离度量标准，从而能更好地契合样本的先验分布。当然，这种性能上的提升是以更多的时空代价换取而来的。

进一步，在表3中给出了10种比较算法在各数据集上的运行时间。从该表可以看出:

（1）对任一算法而言，其运行时间均与样本规模密切相关，样本规模越大，所需花费的时间也越多。

Table 3 Running time of various algorithms表3 各类算法的运行时间比较 s

（2）RUS-ELM算法在每个数据集上所花费的时间几乎都是最少的。这一现象在那些极度不平衡数据集上表现得尤为明显，这主要是大量多数类样本被删除所致。

（3）与ELM算法相比，两种WELM算法的时间开销通常要更大。这主要是由于在式（7）的计算中添加了模糊加权矩阵W所致，且其时间开销与样本规模线性相关。

（4）与ROS-ELM算法相比，SMOTE-ELM算法的时间开销明显要更大。其主要原因在于前者仅是简单复制现有样本，而后者则要做大量的距离计算及排序操作。

（5）本文所提出的几种模糊加权算法的时间复杂度明显高于其他算法。究其原因不难发现，上述算法需对每个样本单独进行计算，进而做个性化的加权操作，因此不可避免地消耗了大量的计算资源。

（6）采用指数化衰减函数的加权算法在时间复杂度上要明显高于采用线性衰减函数的算法。这主要是因为前者增加了一个内部交叉验证的参数寻优过程所致。

接下来，采用FSVM-CIL系列算法[14]与本文算法进行了实验比较。特别地，在FSVM-CIL系列算法中，除使用本文的4种评估函数外，还采用了基于超球中心距离测度的线性衰减评估函数（FSVM-SL）和指数化的衰减评估函数（FSVM-SE）。参照文献[14]的做法，SVM采用RBF核函数，参数通过Grid Search策略确定。鉴于前文已分析得出分类精度不适于评价不平衡学习算法性能的结论，故在本组实验中仅给出了各算法在F-measure和G-mean测度上的实验比较结果，分别如表4和表5所示，其中每个数据集上的最优结果以粗体显示。

从表4及表5的结果可以看出，与FSVM-CIL系列算法相比，本文所提出的FWELM系列算法并未体现出弱势，或者说二者的性能大致相当。具体到F-measure测度，FWELM系列算法在9个数据集上获得

了最优结果，FSVM-CIL系列算法则获得了11个最优结果。而在G-mean测度上，FWELM与FSCM-CIL系列算法在全部20个数据集上所获得的最优结果之比则为12∶8。同时，也观察到在不同数据集上，两类算法所得到的结果往往相差较大，如在vowel0和shuttle_2_vs_5数据集上，FSVM-CIL系列算法的性能要明显优于FWELM系列算法，而在pima和abalone19数据集上，结果则恰好完全相反。相信上述现象的出现是由分类器本身的特性所决定的，ELM和SVM均各自擅长处理不同分布的数据集。此外，在实验中也对上述两个系列算法的运行时间进行了记录，比较结果如表6所示。

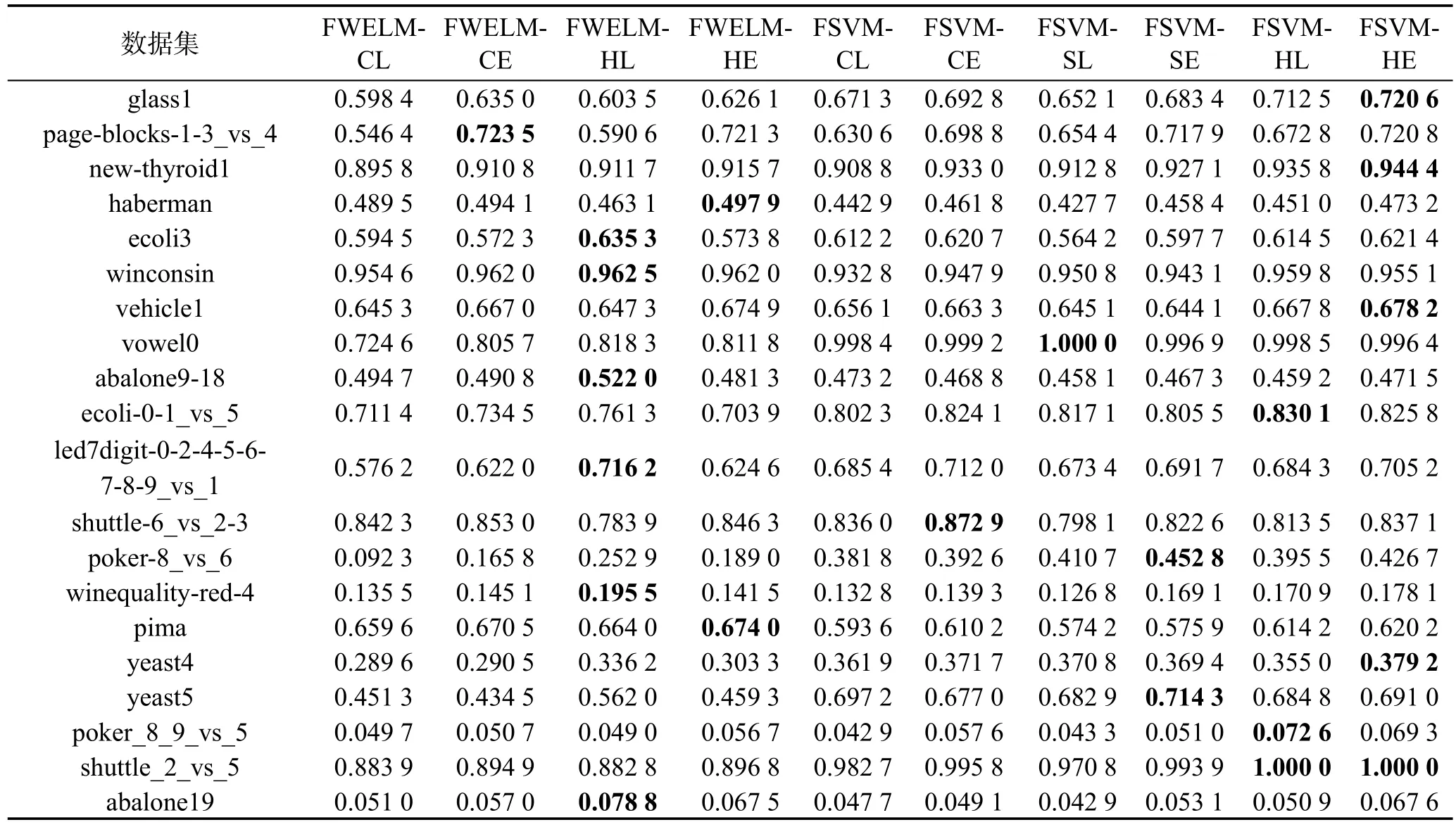
Table 4 Comparative results of FWELM and FSVM-CIL series algorithms on F-measure表4 FWELM与FSVM-CIL系列算法在F-measure测度上的实验比较结果

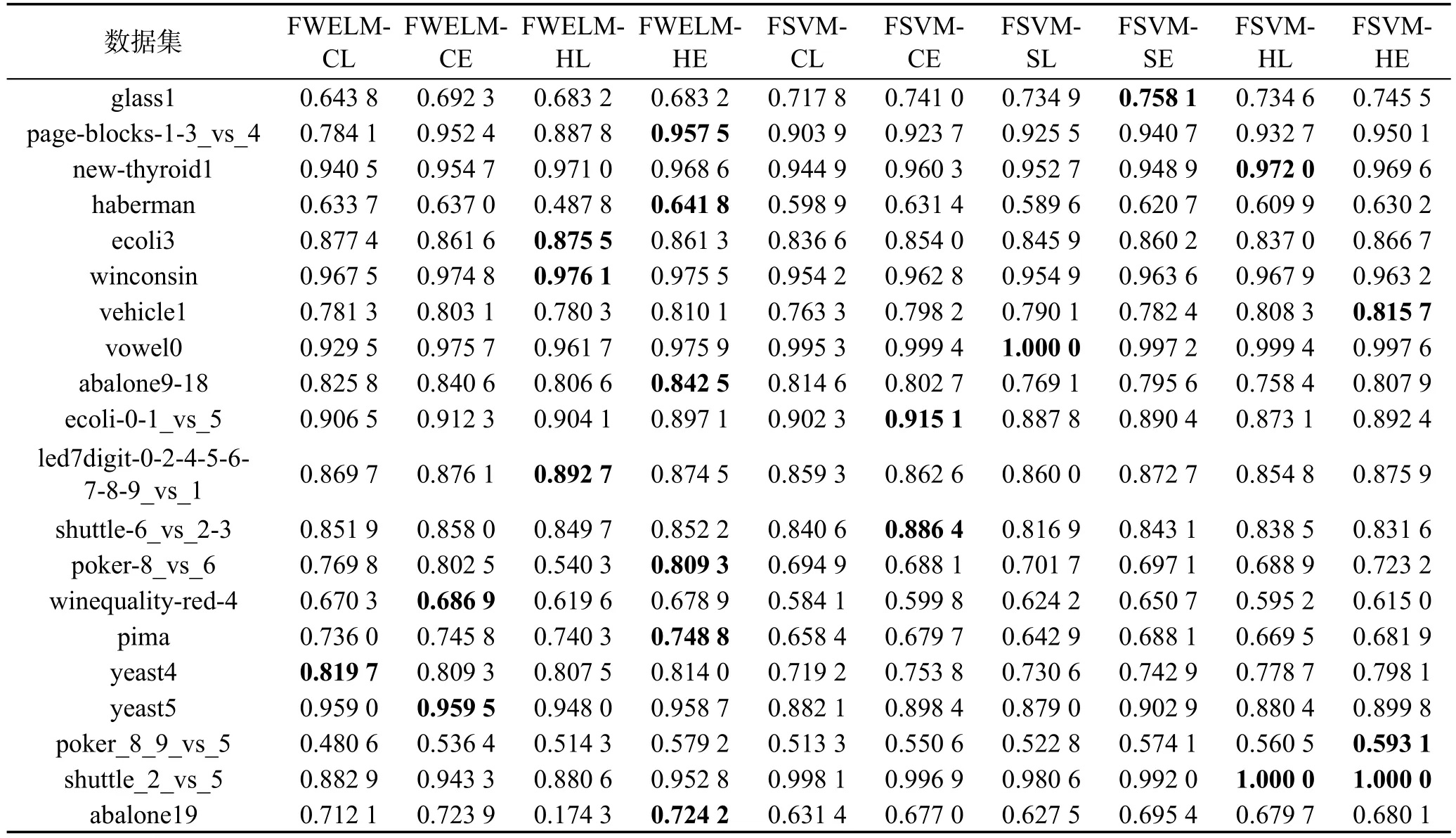
Table 5 Comparative results of FWELM and FSVM-CIL series algorithms on G-mean表5FWELM与FSVM-CIL系列算法在G-mean测度上的实验比较结果

从表6的结果中不难看出，当采用同一评估函数时，FSVM-CIL系列算法往往需要消耗更多的训练时间，且随着样本集规模的增长，特征数的增加，运行时间上的差距也会呈现逐步拉大的趋势。该现象较易从理论上得到解释，因ELM分类器是基于最小二乘的思想，故可直接计算得到，而SVM则需要解决一个相对复杂的二次优化问题。因此与FSVM-CIL系列算法相比，本文所提出的FWELM系列算法有明显更低的时间复杂度，可在一定程度上满足实际应用的需要。

5 结束语

本文从理论上分析了样例不平衡分布对极限学习机性能产生危害的原因，并在该理论框架下探讨了传统的加权极限学习机算法的有效性及其固有缺陷，提出了4种模糊加权极限学习机算法。上述算法能有效抽取训练集中样例的先验分布信息，并据此对各样例的重要度进行评估，从而对每个样例的权重进行模糊化与个性化的设置，以达到排除噪声，离群样例的影响及细化分类面的目的。采用20个二类不平衡数据集对上述方法的有效性与可行性进行了验证，实验结果突出展示了所提算法的以下两个特点：相比采用同种分类器的其他不平衡学习算法，能有效提升分类性能；相比采用不同分类器的同种学习算法，通常具有更小的时空开销。

Table 6 Running time of FWELM and FSVM-CIL series algorithms表6FWELM与FSVM-CIL系列算法的运行时间比较 s

在未来的研究工作中，希望能在以下几方面做一些扩展性的工作：

（1）对现有隶属函数进行改进，将其应用于多类不平衡分类问题。

（2）在充分挖掘全局分布信息的基础上，拟进一步结合样例的局部先验分布信息，设计更为合理的隶属分配函数，从而使分类面得到进一步细化，性能得到进一步提升。

（3）将本文算法应用到各种实际领域中，从而对其有效性做进一步评估。

[1]Huang Guangbin,Zhu Qinyu,Siew C K.Extreme learning machine:theory and applications[J].Neurocomputing,2006, 70(1/3):489-501.

[2]Rumelhart D E,Hinton G E,Williams R J.Learning representations by back-propagation errors[J].Nature,1986,323: 533-536.

[3]Huang Guangbin,Zhou Hongming,Ding Xiaojian,et al.Extreme learning machine for regression and multiclass classification[J].IEEE Transactions on System,Man and Cybernetics:Part B Cybernetics,2012,42(2):513-529.

[4]Huang Gao,Huang Guangbin,Song Shiji,et al.Trends in extreme learning machine:a review[J].Neural Networks, 2015,61:32-48.

[5]Choi K,Toh K A,Byun H.Realtime training on mobile devices for face recognition applications[J].Pattern Recognition,2011,44(2):386-400.

[6]Samat A,Du Peijun,Liu Sicong,et al.E2LMs:ensemble extreme learning machines for hyperspectral image classification[J].IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2014,7(4):1060-1069.

[7]Wan Can,Xu Zhao,Pinson P,et al.Probabilistic forecasting of wind power generation using extreme learning machine[J]. IEEE Transactions on Power Systems,2014,29(29):1033-1044.

[8]Sun S J,Chang C,Hsu M F.Multiple extreme learning machines for a two-class imbalance corporate life cycle prediction[J].Knowledge-Based Systems,2013,39(3):214-223.

[9]Vong C M,Ip W F,Wong P K,et al.Predicting minority class for suspended particulate matters level by extreme learning machine[J].Neurocomputing,2014,128(5):136-144.

[10]Lu Huijuan,An Chunlin,Ma Xiaoping,et al.Disagreement measure based ensemble of extreme learning machine for gene expression data classification[J].Chinese Journal of Computers,2013,36(2):341-348.

[11]Zong Weiwei,Huang Guangbin,Chen Yiqiang.Weighted extreme learning machine for imbalance learning[J].Neurocomputing,2013,101(3):229-242.

[12]Chawla N V,Bowyer K W,Hall L O.SMOTE:synthetic minority over-sampling technique[J].Journal of Artificial Intelligence Research,2002,16(1):321-357.

[13]Zeng Zhiqiang,Wu Qun,Liao Beishui,et al.A classification method for imbalance data set based on kernel SMOTE [J].Acta Electronica Sinica,2009,37(11):2489-2495.

[14]Batuwita R,Palade V.FSVM-CIL:fuzzy support vector machines for class imbalance learning[J].IEEE Transactions on Fuzzy Systems,2010,18(3):558-571.

[15]Yu Hualong,Mu Chaoxu,Sun Changyin,et al.Support vector machine-based optimized decision threshold adjustment strategy for classifying imbalanced data[J].Knowledge-Based Systems,2015,76:67-78.

[16]Maldonado S,Montecinos C.Robust classification of imbalanced data using one-class and two-class SVM-based multiclassifiers[J].Intelligent DataAnalysis,2014,18(1):95-112.

[17]Yu Hualong,Ni Jun.An improved ensemble learning method for classifying high-dimensional and imbalanced biomedicine data[J].IEEE/ACM Transactions on Computational Biology and Bioinformatics,2014,11(4):657-666.

[18]Park Y,Ghosh J.Ensembles of α-trees for imbalanced classification problems[J].IEEE Transactions on Knowledge and Data Engineering,2014,26(1):131-143.

[19]Alcalá-Fdez J,Fernandez A,Luengo J,et al.KEEL datamining software tool:data set repository,integration of algorithms and experimental analysis framework[J].Journal of Multiple-Valued Logic and Soft Computing,2011,17(2/3): 255-287.

[20]Yu Hualong,Sun Changyin,Yang Wankou,et al.AL-ELM: one uncertainty-based active learning algorithm using extreme learning machine[J].Neurocomputing,2015,166:140-150.

[21]Wolpert D H,Macready W G.No free lunch theorems for optimization[J].IEEE Transactions on Evolutionary Computation,1997,1(1):67-82.

附中文参考文献：

[10]陆慧娟,安春霖,马小平,等.基于输出不一致测度的极限学习机集成的基因表达数据分类[J].计算机学报,2013, 36(2):341-348.

[13]曾志强,吴群,廖备水,等.一种基于核SMOTE的非平衡数据集分类方法[J].电子学报,2009,37(11):2489-2495.

YU Hualong was born in 1982.He received the Ph.D.degree in computer science from Harbin Engineering University in 2010.Now he is an associate professor and M.S.supervisor at Jiangsu University of Science and Technology. His research interests include machine learning and data mining,etc.

于化龙（1982—），男，黑龙江哈尔滨人，2010年于哈尔滨工程大学获得博士学位，现为江苏科技大学副教授、硕士生导师，主要研究领域为机器学习，数据挖掘等。发表学术论文50余篇，其中被SCI或EI检索40余篇，主持包括国家自然科学基金、江苏省自然科学基金、国家博士后特别资助计划在内的科研项目7项，参与国家级、省部级及市厅级项目多项。

QI Yunsong was born in 1967.He received the Ph.D.degree in computer science from Nanjing Institute of Technology in 2011.Now he is a professor and M.S.supervisor at Jiangsu University of Science and Technology.His research interests include pattern recognition and signal processing,etc.

祁云嵩（1967—），男，江苏如皋人，2011年于南京理工大学获得博士学位，现为江苏科技大学教授、硕士生导师,主要研究领域为模式识别，信号处理等。发表学术论文20余篇，其中被SCI或EI检索10余篇，主持国家自然科学基金1项，参与各类科研项目多项。

YANG Xibei was born in 1980.He received the Ph.D.degree in computer science from Nanjing Institute of Technology in 2010.Now he is an associate professor and M.S.supervisor at Jiangsu University of Science and Technology.His research interests include machine learning and granular computing,etc.

杨习贝（1980—），男，江苏镇江人，2010年于南京理工大学获得博士学位，现为江苏科技大学副教授、硕士生导师，主要研究领域为机器学习，粒计算等。发表学术论文100多篇，其中被SCI或EI检索60余篇，主持国家自然科学基金2项，江苏省自然科学基金1项，参与各类科研项目多项。

ZUO Xin was born in 1980.She received the Ph.D.degree in computer science from Southeast University in 2014. Now she is a lecturer at Jiangsu University of Science and Technology.Her research interests include pattern recognition and computer vision,etc.

左欣（1980—），女，江苏镇江人，2014年于东南大学获得博士学位，现为江苏科技大学讲师，主要研究领域为模式识别，计算机视觉等。发表学术论文10余篇，其中被EI检索6篇，主持江苏省自然科学基金1项，参与各类科研项目多项。

Research on Class Imbalance Fuzzy Weighted Extreme Learning Machine Algorithm*

YU Hualong1,2+,QI Yunsong1,YANG Xibei1,ZUO Xin1
1.School of Computer Science and Engineering,Jiangsu University of Science and Technology,Zhenjiang,Jiangsu 212003,China
2.College ofAutomation,Southeast University,Nanjing 210096,China
+Corresponding author:E-mail:yuhualong@just.edu.cn

Firstly,this paper analyzes the reason that the performance of extreme learning machine(ELM)is destroyed by imbalanced instance distribution in theory.Then,based on the same theoretical framework,this paper discusses the effectiveness and inherent shortcomings of the weighted extreme learning machine(WELM).Nextly, profiting from the idea of fuzzy set,this paper proposes four fuzzy weighted extreme learning machine(FWELM) algorithms to deal with class imbalance problem.Finally,this paper verifies the effectiveness and feasibility of these four FWELM algorithms by the experiments constructing on 20 baseline binary-class imbalanced data sets.The experimental results indicate that the proposed algorithms can often acquire better classification performance than WELM algorithm and several traditional class imbalance learning algorithms in the context of ELM.In addition,in contrastwith fuzzy support vector machine for class imbalance learning(FSVM-CIL)series algorithms,the proposed algorithms can produce the comparable classification performance,but always consume less training time.

extreme learning machine;class imbalance learning;fuzzy weighting;prior distribution information

10.3778/j.issn.1673-9418.1603094

A

TP183

*The National Natural Science Foundation of China under Grant Nos.61305058,61471182,61572242(国家自然科学基金);the Natural Science Foundation of Jiangsu Province under Grant Nos.BK20130471,BK20150470(江苏省自然科学基金);the Postdoctoral Science Foundation of China under Grant Nos.2013M540404,2015T80481(中国博士后科学基金);the Postdoctoral Research Funds of Jiangsu Province under Grant No.1401037B(江苏省博士后基金).

Received 2016-03,Accepted 2016-05.

CNKI网络优先出版:2016-05-19,http://www.cnki.net/kcms/detail/11.5602.TP.20160519.1513.008.html

YU Hualong,QI Yunsong,YANG Xibei,et al.Research on class imbalance fuzzy weighted extreme learning machine algorithm.Journal of Frontiers of Computer Science and Technology,2017,11(4)：619-632.