深部开采松软煤层抽采钻孔变形特性研究*

张学博，高建良

(1.煤炭安全生产河南省协同创新中心，河南 焦作 454003；2.河南省瓦斯地质与瓦斯治理重点实验室 —省部共建国家重点实验室培育基地，河南 焦作 454003；3.河南理工大学 安全科学与工程学院，河南 焦作 454003)

0 引言

深部开采的松软煤层具有应力高、力学强度低、瓦斯大且解吸速度快、煤层厚度变化较大等特征，抽采钻孔在松软煤层施工时，经常出现喷孔、顶钻、卡钻等动力现象，常会出现大范围塌孔，形成钻穴[1]；成孔后，钻孔孔壁也会发生变形、冒落、坍塌，导致孔径缩小或者闭合，阻断瓦斯涌出和流动的通道[2-3]，严重影响了瓦斯抽采效率。研究高应力松软煤层抽采钻孔变形失稳特征，对解决高应力松软煤层钻孔失稳坍塌问题、有效提高瓦斯抽采效果有着重要的理论指导意义。

国内外许多学者对抽采钻孔周围煤岩的变形失稳规律等相关理论进行了研究[3-8]。Tezuka等[3]提出了一些钻孔稳定性模型，并基于这些模型对钻孔壁的稳定性进行理论分析；王振[4]基于理论分析建立了掘进面防突钻孔失稳力学模型，研究了孔底和孔壁附近煤体破坏形式及失稳特征；赵阳升[5]等对含钻孔花岗岩体内在恒温恒压下钻孔变形规律及其临界失稳条件进行研究，运用黏弹塑性力学理论建立了钻孔变形的黏弹性理论模型及黏弹-塑性理论模型；翟成[6]、王睿[7]通过对矿井松软突出煤层钻孔失稳变形机理的分析指出了导致钻孔变形失稳主要因素；郝富昌[8]根据建立的黏弹塑性软化模型模拟分析了软硬煤层中钻孔卸压效果，研究了孔径的变化规律。前人大都是对钻孔失稳前变形特征等进行了研究，而对于抽采钻孔变形失稳过程及失稳后的相关规律尚未进行研究；本文拟对高应力松软煤层抽采钻孔变形失稳过程中及失稳后周围煤体应力变化、位移变化、透气性分布等特征进行研究，这对优化抽采钻孔布置、提高瓦斯抽采效果、有效防治瓦斯灾害有着重要的理论指导意义。

1 抽采钻孔变形失稳数值分析方法及模型参数

1.1 理论模型建立

本文采用一种用连续介质力学方法解决非连续介质力学问题的新型数值分析工具RFPA2D系统对钻孔变形失稳过程进行模拟分析。RFPA2D 系统可以有效地将数值计算方法与损伤力学结合起来，充分考虑岩石的非均匀性，常用来模拟岩石变形、失稳和破裂的非线性行为。

1.1.1 基本控制方程

本文模型基于如下基本假设：

1)煤岩体是非均匀的，煤岩体细观单元体的损伤参量符合Weibull分布：

(1)

式中：α和α0分别为材料微元体力学性质(如弹性模量、强度等) 和力学性质平均值；m为均质度系数，m越大，煤岩体越均质，反之，则越不均质。

2)岩石中细观单元体是弹脆性的，并有残余强度，其力学行为用弹性损伤理论描述，最大拉应变准则和Mohr-Coulomb准则作为损伤阑值条件。

平衡方程：

(2)

几何方程：

εij=(ui,j+uj,i)/2εv=ε11+ε22+ε33

(3)

本构方程：

σij'=λδijεv+2Gεij

(4)

1.1.2 煤岩体本构关系的细观统计损伤模型

基于煤岩体受力后不断损伤引起微裂纹萌生和扩展造成其应力-应变曲线为非线性，可以将岩石的细观单元的力学性质用弹性损伤力学的本构关系来描述，按照应变等价原理，受损材料单元体本构关系可以通过无损材料中的名义应力得到，即：

ε=σ/E=σ(1-D)E0

(5)

式中：E0和E分别为损伤后单元的初始弹性模量和弹性模量；D为反映损伤程度的损伤变量。

煤岩体细观层次上的破坏被视为拉伸和剪切破坏，其单元体被拉伸和压缩时，单元体损伤变量D可以分别用下述公式描述[9]：

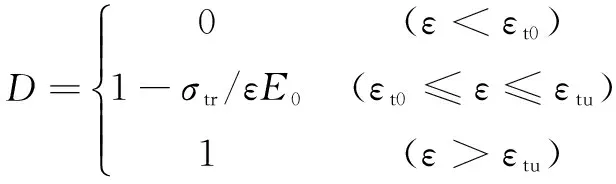
(6)

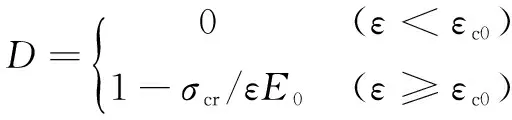
(7)

式中：σtr为拉伸损伤残余强度；εt0为弹性极限拉应变；εtu为最大拉应变；σcr为剪切损伤残余强度；εc0为压应变的弹性极限。

1.2 物理模型建立

据弹性力学理论可知，计算域应不小于巷道半径5倍，这里取20倍，钻孔半径取值50 mm，模型中煤层尺寸为1 000 mm×1 000 mm，网格划分200×200个单元。由于钻孔长度远大于孔径故可以将其简化为平面应变模型来研究，加载方式采用固定载荷，侧压系数为1.0。建立的物理模型图如图1 所示。

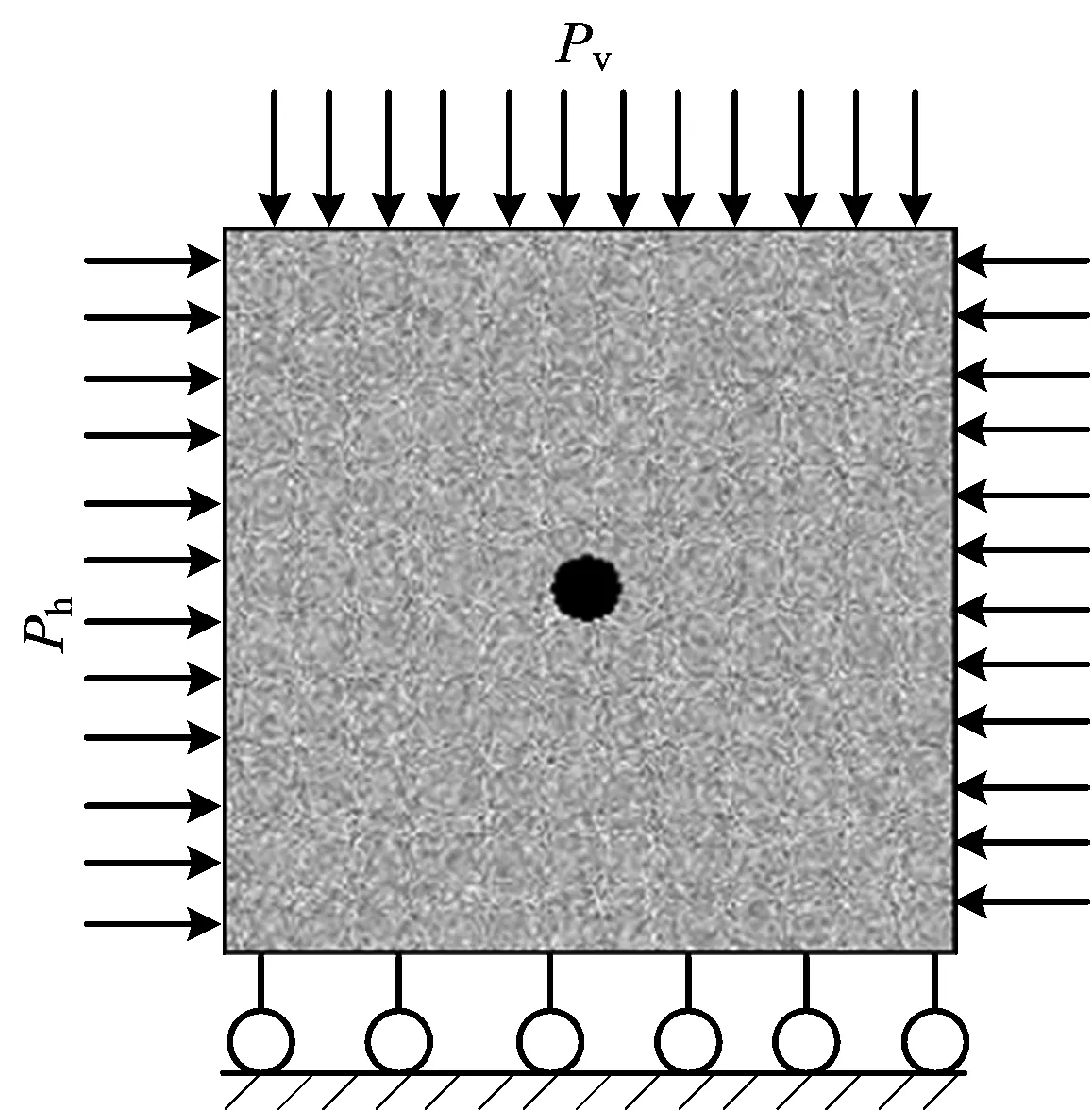
图1 物理模型Fig.1 Numerical simulation model

1.3 模拟参数确定

RFPA系统用均质度系数m来表征材料的均匀程度，均质度系数m将岩体宏观力学特性与细观力学性质密切联系起来，可根据下面拟合公式对输入的弹性模量和岩体强度进行选取。

(8)

(9)

式中：Es0和fs0表示模拟分析采用的弹性模量和强度的均值；Es和fcs分别为煤岩体实际的弹性模量和强度。

某矿煤层埋深1 000 m左右，按照平均重度27 kN/m3，可计算得其垂直应力为27.0 MPa，侧压系数为1.0，故其水平应力也为27.0 MPa；其煤质非常松软，实测其煤样坚固性系数0.7，弹性模量2 000 MPa，单轴抗压强度7.3 MPa；m值取6，由式(1)、(2)可得弹性模量和单轴抗压强度的模拟输入值分别为4 086，8.1 MPa；其他模拟所需参数见表1所示。

表1 煤的物理力学参数

2 深部开采松软煤层抽采钻孔变形特性研究

利用RFPA2D系统数值模拟了深部开采松软煤层抽采钻孔变形失稳过程，以下分别从钻孔周围煤体应力及形变分布、卸压区演化、位移变化和透气性分布规律五个方面反映抽采钻进变形失稳特征。

2.1 钻孔周围煤体应力分布及演化规律

数值解算得到钻孔周围煤体最大主应力分布如图2所示，图中灰度表示应力值大小，颜色越深应力值越小。

图2 最大主应力分布Fig.2 Maximum principal stress distribution

由图2可以看出，深部开采的高应力松软煤层抽采钻孔施工后，由于孔壁周围煤体径向应力突然解除，钻孔周围应力重新分布，钻孔周边产生的竖直挤压和水平挤压作用，使孔壁周围形成应力集中区；在集中应力作用下，孔壁附近煤体率先发生屈服，形成塑性区；然后，应力集中区向钻孔外部移动，孔壁附近塑性状态的煤体变形量不断增大，孔壁附近塑性状态煤体变形量比远处塑性状态煤体要大，当其达到变形极限时，孔壁附近塑性状态煤体就会破裂，形成破裂区。破裂区内部煤体的强度明显削弱(低于原岩应力)；随着塑性区及破裂区煤体变形量的不断增加，破裂区煤体的强度进一步降低，当煤块间的摩擦力无法抵抗煤体的变形压力及自重时，钻孔周围破裂煤体将向钻孔内坍塌，即塌孔发生。最终，钻孔由内而外形成破裂区、塑性区、弹性区，钻孔引起的卸压区主要集中在破裂区范围内。

从钻孔周围裂隙发育情况来看，钻孔附近的塑性区内煤体首先产生一些微孔/微裂隙，然后随着塑性区内煤体变形量的不断增大，微裂隙逐渐贯通形成较大的次生裂隙，次生裂隙逐渐增多并贯通；最后破裂区煤体形成大宏观裂纹导致钻孔周围煤体失稳垮塌，紧邻钻孔周围煤体形成垮塌区和破碎区。总体来说，钻孔破坏形式为上方发生垮塌，形成垮塌区；左右侧发生破坏，形成破碎区，这与胡胜勇[10]博士的钻孔孔壁附近煤岩体破坏全过程的相似试验结果基本相同，也验证了数值模拟结果的正确性。

2.2 钻孔周围煤体卸压区演化规律

为了进一步研究钻孔周围卸压区演化规律，过钻孔中心做一水平截线，该截线上最大主应力及切应力分布及演化如图3，4所示。

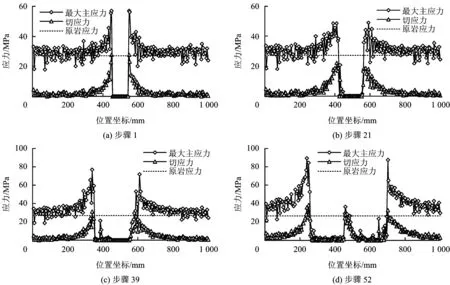
图3 钻孔周围应力动态分布Fig.3 Dynamic distribution of the stress around the borehole

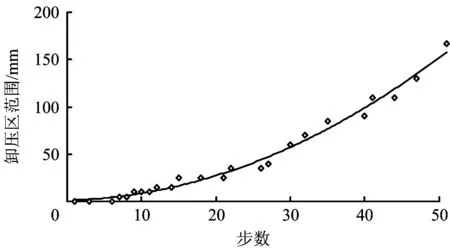
图4 钻孔周围煤体卸压区变化Fig.4 The change of coal unloading zone around the borehole

由图3，4容易看出，钻孔附近煤体应力集中区应力较大，距钻孔越远，煤体应力越低，主应力逐渐接近原始应力；随着时间的延长，应力集中区不断向钻孔外侧移动，钻孔附近卸压区内应力降低，钻孔周围卸压范围不断变大，卸压范围由0(step1)——35(step21)——90(step39)——167 mm(step52)，总体而言由钻孔变形失稳引起的周围煤体的卸压区域较小。此外，由图3(d)可以看出，钻孔失稳坍塌后，由于钻孔顶部煤体不断下移，钻孔内煤体不断压实，使得孔内煤体最大主应力也由开始的0 MPa变成了36.6 MPa，切应力也由0 MPa变成了28.0 MPa。

2.3 钻孔周围煤体形变分布及演化规律

钻孔周围煤体形变分布如图5所示，图5中箭头大小表示位移大小，箭头方向表示位移方向。

图5 钻孔周围煤体形变分布Fig.5 The deformation distribution of coal around the borehole

由图5可以看出，钻孔施工完毕后，钻孔周围煤体逐渐向钻孔移动，即上部煤体下移、下部煤体上移，左侧煤体右移、右侧煤体左移，钻孔附近煤体位移量较大，远处煤体位移量相对较小；随时间的增加总位移量不断增加，钻孔面积不断减小最后基本变为零，这说明钻孔最后被周围煤体堵死(即堵孔)；受竖直方向地应力及自身重力影响，钻孔上方煤体下移量略大于下方煤体上移量，钻孔左右侧水平位移相差不大。

2.4 钻孔孔壁位移变化规律

为了进一步的研究钻孔孔壁变形情况，分别在钻孔顶、底部及两侧设置监测点，各监测点位移情况如图6～8所示。

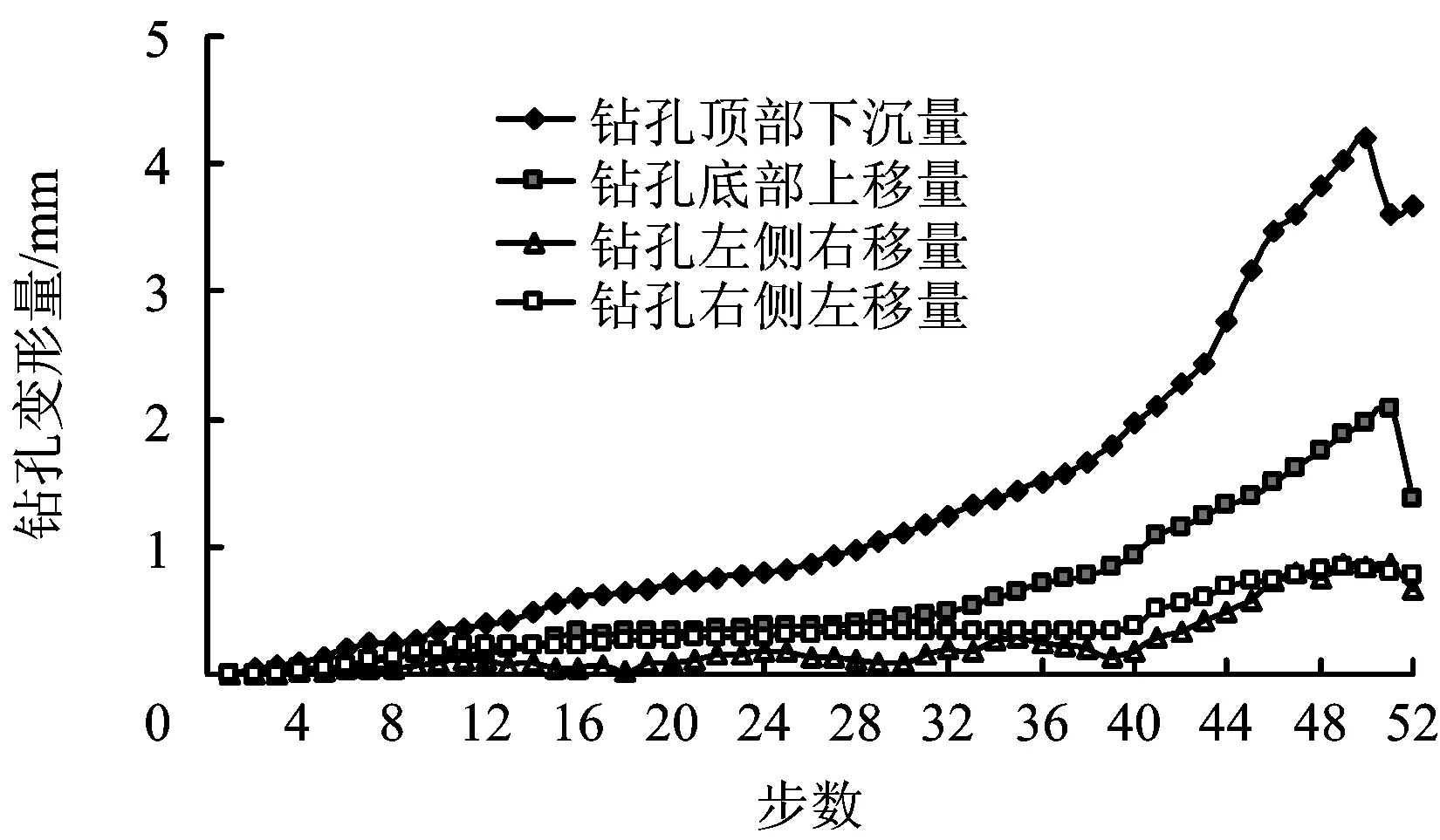
图6 钻孔孔壁位移变化Fig.6 The variation of coal displacement around the borehole

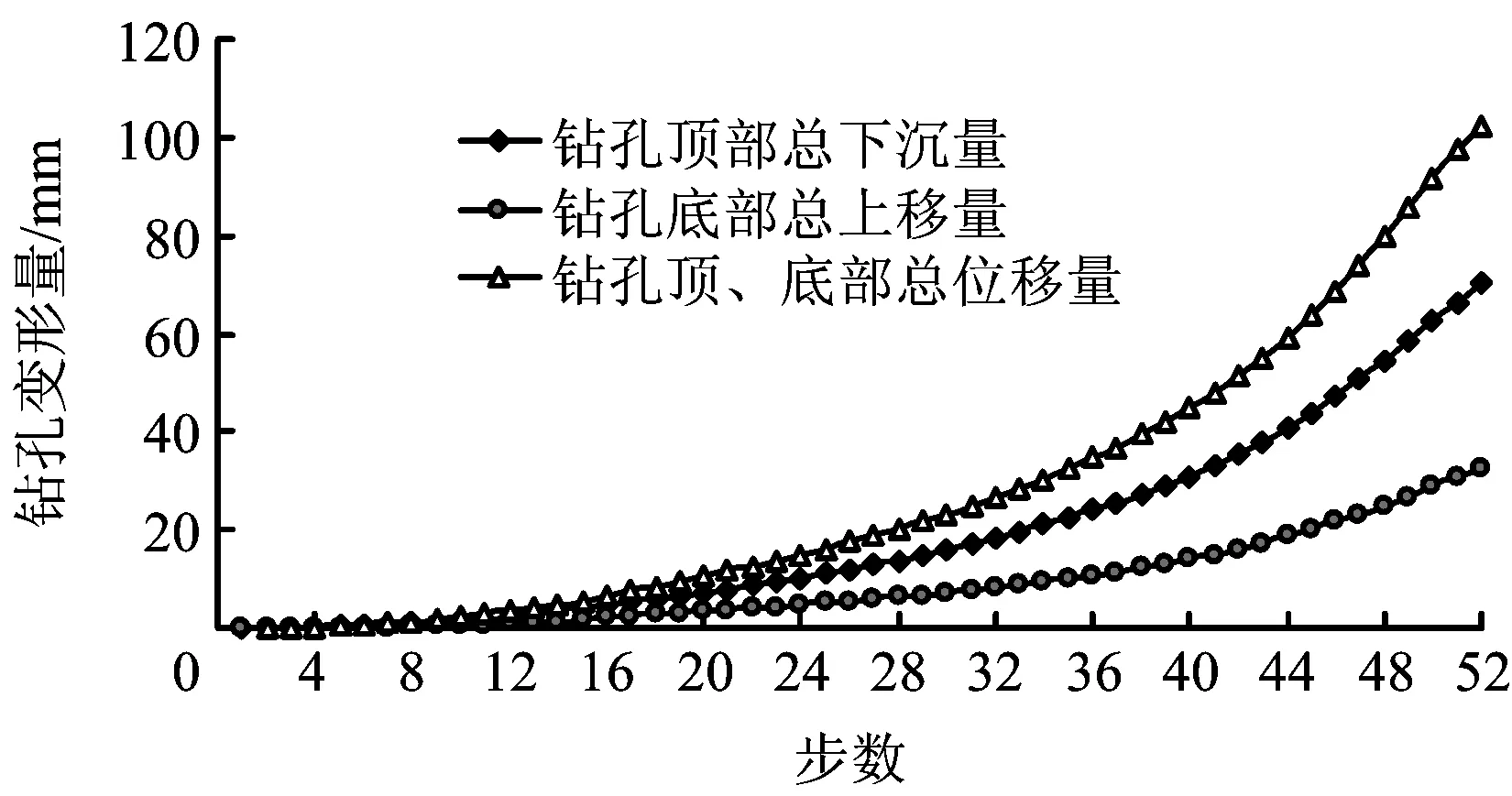
图7 钻孔孔壁顶、底部总位移变化Fig.7 The variation of coal total displacement on top and bottom of borehole

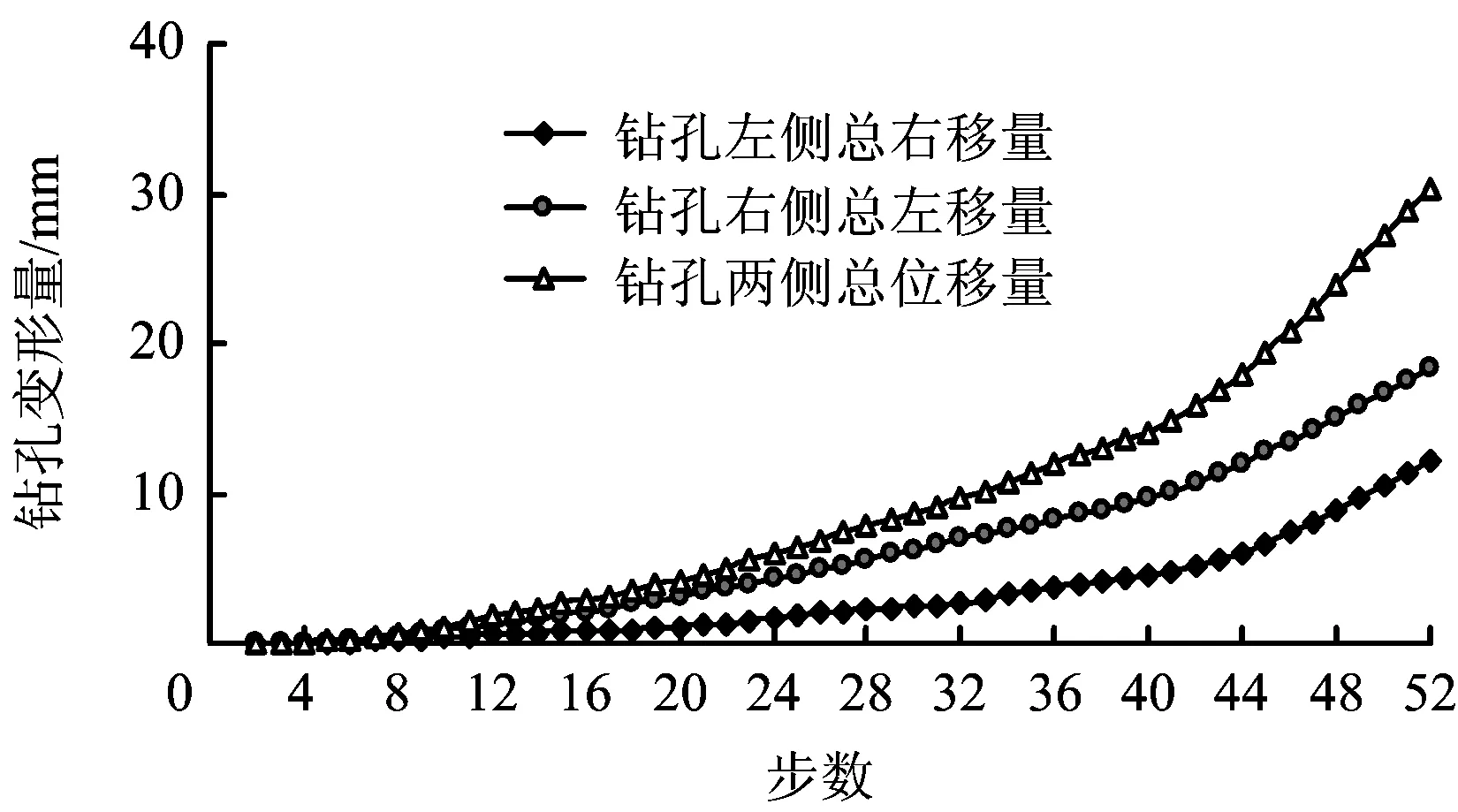
图8 钻孔孔壁顶、底部两帮总位移变化Fig.8 The variation of coal total displacement on both sides of borehole

从图6，7中可以看出，随解算步数的增加，孔壁顶、底部垂直位移整体呈先增加然后再降低的变化趋势；开始阶段(step1～28)，钻孔顶部煤体垂直位移量比较小且增长速度较小，该阶段为钻孔失稳前弹性变形阶段；然后随着时间的延长(step28～50)，其垂直位移量不断增加且位移量增长速度逐渐变大，该阶段为钻孔逐渐失稳过程；最后(step50～52)，垂直位移量开始降低，该阶段为钻孔失稳后孔内煤体压缩阶段；钻孔顶、底部煤体总垂直位移均是随解算步数的增加不断增加，钻孔顶部煤体下移量最后达到70.1 mm，底部煤体上移量为32.3 mm，二者位移之和为102.4 mm大于钻孔直径100.0 mm，说明钻孔已经坍塌。

从图6，8中可以看出，孔壁两侧水平位移随解算步数的增加大致呈先增加再降低的变化趋势，其总位移均是随解算步数的增加不断增加，左右两侧总水平位移量分别是12.1，18.3 mm，二者位移之和为32.4 mm；可见其两侧水平位移量远远小于顶底部位移垂直位移量。由此可知，钻孔变形失稳过程中，钻孔的形状由开始的准圆形逐渐变成“类橄榄球形”，然后钻孔“类橄榄球形”断面逐渐减小至坍塌。

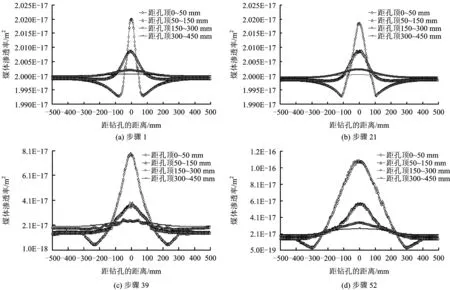
图9 钻孔周围煤体渗透率分布Fig.9 Distribution of coal's permeability around the borehole

2.5 钻孔变形失稳过程中周围煤层渗透特性研究

大量的受载含瓦斯煤岩体渗透实验结果可知，煤岩体变形破坏过程可以分为孔隙/裂隙压密阶段、弹性变形阶段、屈服变形及峰值强度阶段和残余强度变形阶段4个阶段，前2个阶段煤岩体体积减小渗透率降低，后2个阶段煤岩体体积增大渗透率增加，渗透率总体表现出一种先降低后增加的“V”字型的发展趋势。因此，可以基于煤体体积应变来研究煤体变形过程中的渗透特性。

煤体孔隙率与有效应力、孔隙应力等有关，如果仅考虑有效应力导致的煤体孔隙率变化，则煤体孔隙率可表示为[11]：

(10)

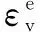
煤层渗透率大小与煤体体积应变的关系可以通过Kozeny-Carman方程推导得出，通过推导可以得到[12]：

(11)

这里以钻孔上部煤体为例研究钻孔失稳过程中周围煤体渗透演化特性，在钻孔上部煤体内设置5条水平监测线，将其划分4个煤体监测区，分别监测该区域的变形情况，以计算该区域的渗透率；煤体初始孔隙率和初始渗透率分别为0.04和2×10-17m2，得到钻孔变形失稳过程中钻孔上部煤体渗透率分布规律如图9所示。

从图9中可以看出，在钻孔变形失稳坍塌过程中，由于钻孔附近煤体的变形量不断增加及裂隙的不断贯通，使得周围钻孔附近煤体渗透率逐渐增大，钻孔周围煤体渗透率变化量及变化范围不断增加；step1，step21，step39，step52时，钻孔上部煤体渗透率最大值分别是初值的1.01，1.38，3.93，5.42倍。

钻孔失稳前后上部煤体渗透率分布均大致呈“V”字型变化规律，即钻孔附近煤体渗透率变化较大，钻孔正上方煤体渗透率最大，钻孔两侧煤体渗透率随着距离钻孔水平距离的增加呈先减小后增加然后趋于稳定的趋势，在部分区域煤体渗透率甚至减小。这与文献[11]根据建立的考虑有效应力变化、瓦斯解吸和煤基质收缩效应的煤层渗透率动态变化模型数值模拟得到的煤层瓦斯抽采过程中煤体透气性动态演化规律结果是一致的，也证明了本文研究结果的正确性。

3 结论

1)得到了钻孔变形失稳过程中周围煤体应力分布及演化规律、卸压区演化规律和裂隙发育特征。 钻孔破坏形式为上方发生垮塌，形成垮塌区；左右侧发生破坏，形成破碎区，通过与前人相似实验结果的对比验证了数值模拟结果的正确性。

2)揭示了钻孔周围煤体形变分布及演化规律和孔壁位移变化规律。钻孔周围煤体均向钻孔移动，钻孔附近煤体位移量较大，远处煤体位移量相对较小；孔壁顶、底部垂直位移和两侧煤体水平位移随时间的增加整体均呈先增加然后再降低的变化趋势，总位移均是随时间的增加不断增加；孔壁上方下移量略大于下方上移量，孔壁左右侧水平位移相差不大；钻孔变形失稳坍塌过程中，钻孔形状先有开始的“准圆形”变成“类橄榄球形”，接着呈“类橄榄球形”不断缩径，然后发生失稳，最后钻孔上部煤体发生坍塌。

3)钻孔失稳过程中，钻孔附近煤体渗透率逐渐增大，钻孔周围煤体渗透率变化量及变化范围均不断增加；周围煤体渗透率分布均大致呈“V”字型变化规律，即呈随着距钻孔距离的增加先减小后增加然后趋于稳定的趋势，通过与前人研究结果的对比证明了研究结果的正确性。

[1] 孙玉宁,王永龙,翟新献,等. 松软突出煤层钻进困难的原因分析[J]. 煤炭学报, 2012,37(1) :117-121.

SUN Yuning, WANG Yonglong, ZHAI Xinxian, et al. Analysis on reasons of drilling difficulty in soft and outburst coal seam[J] . Journal of China Coal Society, 2012, 37(1) : 117-121.

[2] 刘春.松软煤层瓦斯抽采钻孔塌孔失效特性及控制技术基础[D]. 徐州：中国矿业大学, 2014.

[3] TEZUKA K,NIITSUMA H. Stress estimated using micro seismic clusters and its relationship to the fracture system of the Hijiori hot dry rock reservoir[J]．Engineering Geology，2000，56(3)：47-62．

[4] 王振,梁运培,金洪伟．防突钻孔失稳的力学条件分析[J]．采矿与安全工程学报,2008,25(4)：444-448.

WANG Zhen, LIANG Yunpei, JIN Hongwei. Analysis of mechanics conditions for instability of outburst-preventing borehole[J]. Journal of Mining & Safety Engineering, 2008, 25(4):444-448.

[5] 赵阳升,峪保平,万志军,等.高温高压下花岗岩中钻孔变形失稳临界条件研究[J]．岩石力学与工程学报,2009，28(5)：865-874.

ZHAO Yangsheng, YU Baoping, WAN Zhijun, et al. Study of critical condition of borehole instability in granite under high temperature and high pressure [J]. Chinese Journal of Rock Mechanics and Engineering, 2009，28(5)：865-874 .

[6] 翟成,李全贵,孙臣，等.松软煤层水力压裂钻孔失稳分析及固化成孔方法[J].煤炭学报,2012, 39(9):1431-1436.

ZHAI Cheng, LI Quangui, SUN Chen, et al. Analysis on borehole instability and control method of pore forming of hydraulic fracturing in soft coal seam [J]. Journal of China Coal Society, ,2012, 39(9):1431-1436.

[7] 王睿,袁岽洋,张进增,等.基于Hoek-Brown强度准则的隧道围岩松动圈分析[J]．中国安全生产科学技术,2017,13(3)：121-126.

WANG Rui,YUAN Dongyang， ZHANG Jinzeng， et al. Analysis on broken zone of surrounding rock in tunnel based on Hoek-Brown strength criterion.[J]. Journal of Safety Science and Technology ,2017,13(3)： 121-126.

[8] 郝富昌,支光辉,孙丽娟.考虑流变特性的抽放钻孔应力分布和移动变形规律研究[J]．采矿与安全工程学报,2013,30(3)：449-455.

HAO Fuchang, ZHI Guanghui, SUN Lijuan. Stress distribution and movement law around drainage borehole when considering rheological property [J]. Journal of Mining & Safety Engineering, 2013，30(3)：449-455.

[9] 唐春安．采动岩体破裂与岩层移动数值试验[M]．长春：吉林大学出版社，2003．

[10] 胡胜勇.瓦斯抽采钻孔周边煤岩渗流特性及粉体堵漏机理[D]. 徐州：中国矿业大学, 2014.

[11] 王登科,彭明,付启超,等.瓦斯抽采过程中的煤层透气性动态演化规律与数值模拟[J]．采矿与安全工程学报,2016,35(4)：704-712.

WANG Dengke, PENG Ming, FU Qichao, et al. Evolution and numerical simulation of coal permeability during gas drainage in coal seams [J]. Journal of Mining & Safety Engineering, 2016，35(4)：704-712.

[12] 冉启全，李士伦. 流固耦合油藏数值模拟中物性参数动态模型研究[J]. 石油勘探与开发，2003，24(3)：61-65.

RAN Qiquan，LI Shilun. Study on dynamic models of reservoir parameters in the coupled simulation of multiphase flow and reservoir deformation[J]. Petroleum Exploration and Development，2003，24(3)：61-65.