油气井特殊螺纹接头连接安全性研究*

莫 丽，涂 炼，付 强，王 磊

(1.西南石油大学 机电工程学院，四川 成都 610500；2.中海油田服务股份有限公司 油田生产事业部完井中心，天津 300459)

0 引言

螺纹接头是油套管的连接部位，同油套管柱一起在井下长期承受拉伸、压缩、内压、外压等复合载荷的作用[1]。螺纹连接部位是油套管柱中最薄弱的环节，据调研，国外油套管失效事故中，64%都发生在螺纹连接处，而国内则比例更高，约为86%。因此，提高油套管螺纹的连接质量是确保油套管柱质量的关键因素之一[2-3]。

随着石油开采技术的进步，国内外出现了许多深井、超深油气井的开发，API螺纹接头由于自身性能的限制，连接强度已不能满足工业要求[4]，而特殊螺纹接头虽然比API螺纹连接强度高，但依然存在上卸扣过程中易粘扣的问题[5-6]，另外常规特殊螺纹多采用单级金属对金属密封结构，在超深井及高压气井中密封安全性难以保证。针对以上问题，设计了新型特殊螺纹接头，采用倒钩型螺纹，同时改进螺纹及密封面参数来提高螺纹的连接和密封性能。另外，以往特殊螺纹连接性能的研究只从单一方面进行分析，文献[7-8]研究了螺纹滑脱失效的过程，获得了滑脱过程的力学机理及产生的原因，文献[9]通过实验和有限元方法证明了储气井螺纹抗疲劳性能达到了使用要求，文献[10-11]分析了螺纹接头的连接的极限强度问题，关于连接性能的综合分析较少。因此，本文采用有限元和全尺寸试验相结合的方法，综合分析了螺纹接头在5种不同工况下的连接安全性。研究内容为特殊螺纹的设计和安全使用提供重要的参考价值。

1 有限元建模

1.1 模型简化

管体规格为φ88.9 mm×6.45 mm，螺纹为承载面角度为-5°，导向面角度为10°的倒钩型螺纹，内螺纹齿高为1.2mm，外螺纹齿高为1.0mm，该螺纹参数与API螺纹参数[12]差别较大，如表1所示。

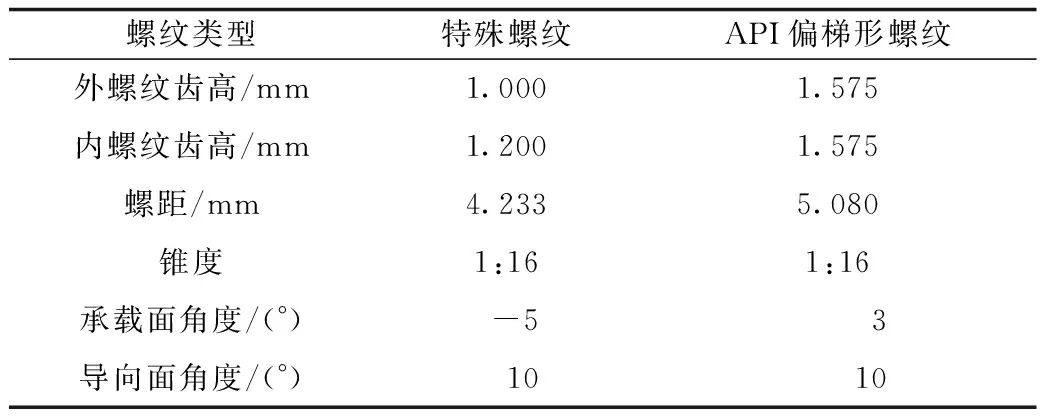
表1 特殊螺纹与API偏梯形螺纹齿形参数对比

接头主密封结构采用锥面对锥面和柱面对球面的组合密封形式，扭矩台肩为-15°逆向台肩。公、母螺纹啮合后，公螺纹的齿顶和母螺纹的齿底间存在一定的间隙，能储存丝扣油同时降低齿顶和齿底的接触应力，螺纹啮合后，结构示意图如图1所示。

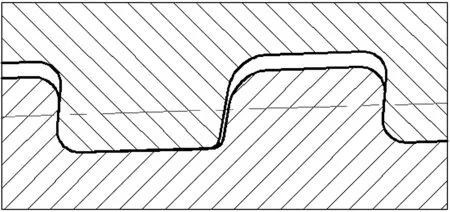
图1 特殊螺纹齿形Fig.1 The tooth profile of the premium thread

因该螺纹螺旋升角较小，忽略螺旋升角对计算结果的影响[13]，把接头简化为轴对称结构。采用二维轴对称模型来对接头进行有限元建模，考虑到圣维南效应，建模时所取的管体长度为管体小端至螺纹消失点距离的2倍。为便于计算结果的处理及比较，需对螺纹的扣牙编号。扣牙号以公接头为准，从公接头靠近密封面的首扣开始为1号扣牙，整体螺纹共有17扣，该特殊螺纹接头建模如图2所示。

图2 特殊螺纹接头几何建模Fig.2 Geometric model of double primary sealing connection

采用CAX4I四节点双线性轴对称四边形单元对模型进行网格划分，并对螺纹连接部分、密封面及扭矩台肩进行网格细化。螺纹局部网格划分如图3所示。

图3 局部网格划分Fig.3 Local mesh partition

1.2 材料力学性能

接头采用2Cr13材料进行加工，并经过热处理，处理到API L80钢级。在加工好的接头中随机取出样品，实测其屈服强度、抗拉强度及延伸率，测量结果如表2所示。2Cr13为合金钢，材料的弹性模量206 GPa，泊松比为0.3。密封面接触时采用库伦摩擦模型，摩擦因数一般取0.02[14]。

表2 材料力学性能

1.3 边界条件

根据接箍的对称性，接箍中面的轴向位移为零，因此在接箍对称中面的各结点上施加轴向位移约束，径向方向自由。接头上扣扭矩通过施加过盈量来模拟，轴向力则转化为均布载荷施加在管体大端，其计算公式为：

(1)

式中：Fa为轴向应力，MPa；F为轴向力，kN；d0为管体外径，mm；d1为管体内径，mm。

螺纹接头在井下会承受复杂的载荷，不同工况载荷的不同，对接头连接性能会产生不同的影响，其中极限载荷取螺纹的极限强度。因接箍和管体采用同种材料，屈服强度均为618 MPa。管体内径76 mm，接箍外径为107.95 mm，接箍内径为76 mm。按照文献[15]中相关强度公式，代入数据，经计算得到接头的抗拉强度为1 032.5 kN，抗压缩强度为861.8 kN，抗内压强度为78.5 MPa，抗外挤强度为83.2 MPa。极限载荷按极限强度理论计算值施加，具体的加载情况如表3所示。

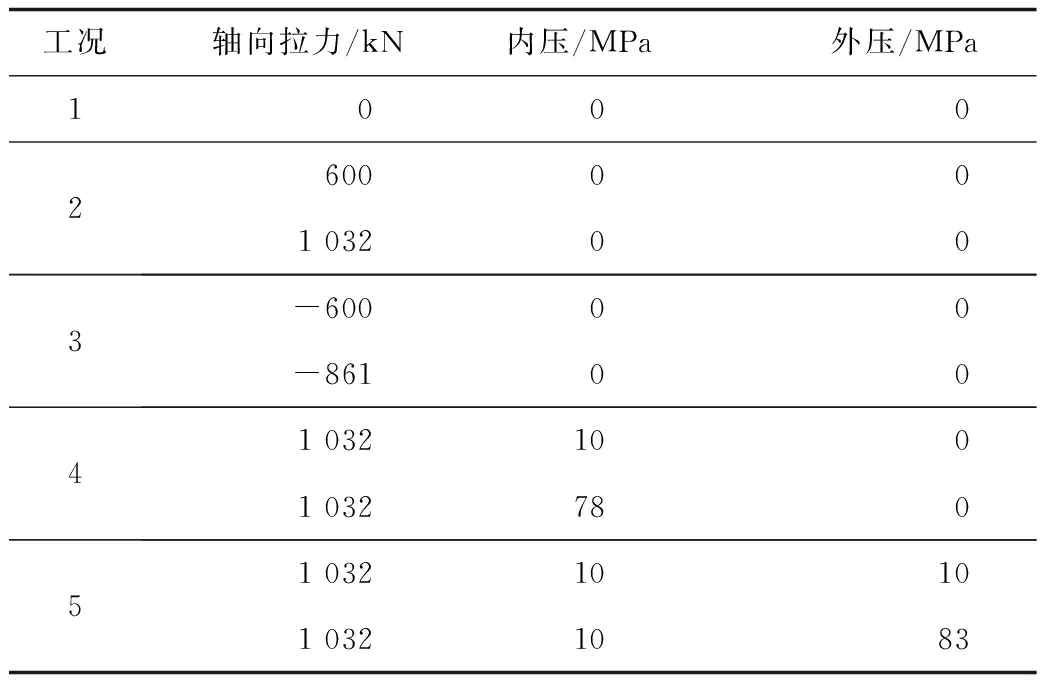
表3 加载工况

2 有限元结果分析

2.1 上扣分析

采用施加过盈量的方法来模拟接头上扣后的状态，在螺纹段施加过盈量0.13 mm，锥面对锥面密封段施加过盈量0.10 mm，柱面对球面密封段施加过盈量0.08 mm，台肩施加过盈量0.03 mm。上扣后螺纹接头Mises应力云图如图4所示，螺纹最大应力分布如图5所示。

图4 上扣后Mises应力分布Fig.4 Distribution of Mises stress after make-up

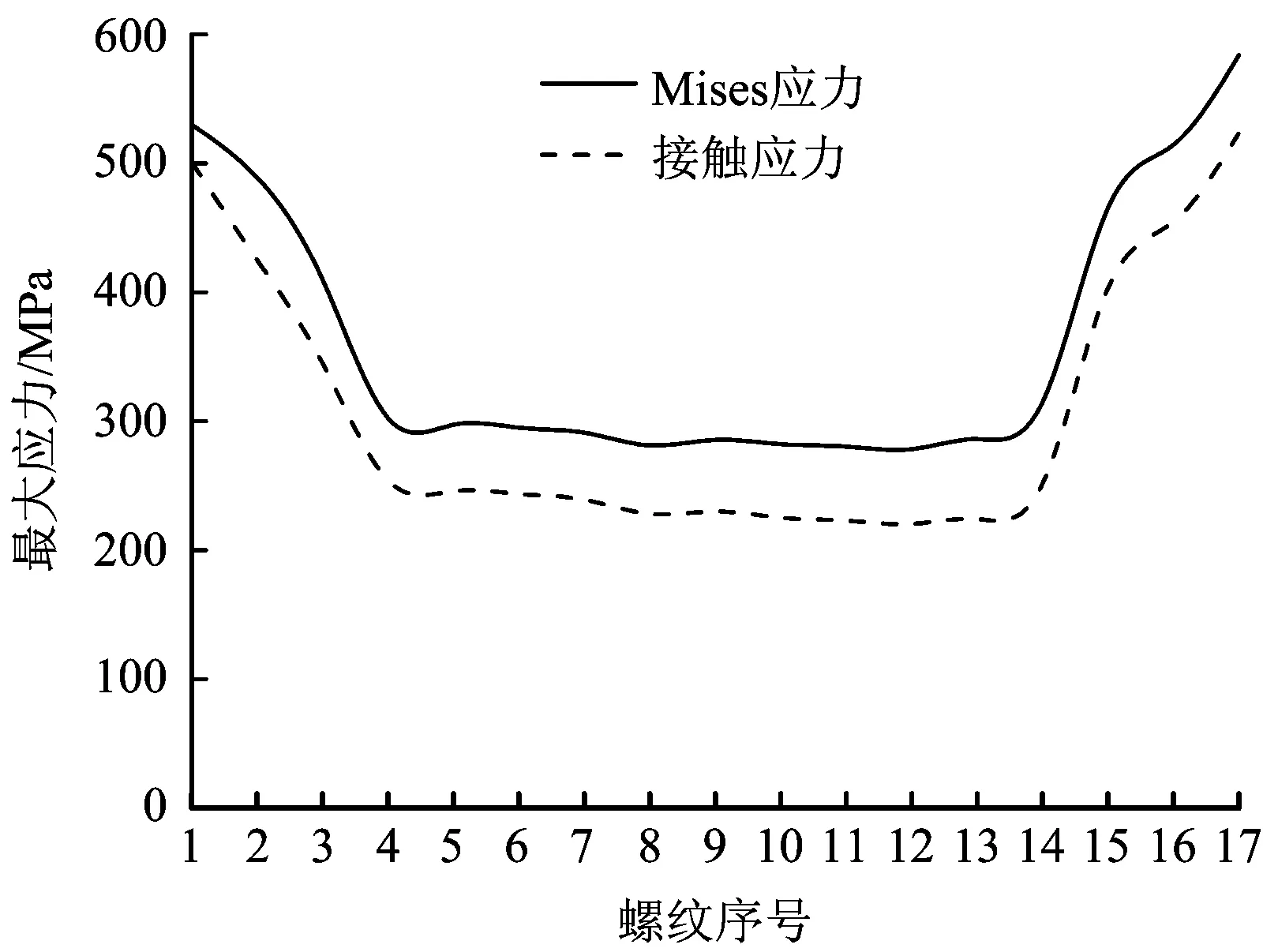
图5 上扣后螺纹最大应力分布Fig.5 The maximum stress distribution of the threads after make-up

由图4可知，上扣后螺纹段和密封面都产生了挤压作用，在台肩和球面密封段应力较大，最大的Mises应力出现在台肩与锥面密封的过渡段，达到649 MPa，已经超过材料的屈服极限，但是，螺纹段的应力以及密封面的应力并没有超过屈服极限，接头承载能力以及密封性能并没有被破坏。

由图5可知，上扣后，螺纹最大Mises应力及接触应力呈“凹槽形”分布，首尾3扣出现明显的应力集中，中间段螺纹应力分布均匀。接触应力及Mises应力最大值均出现在公扣大端，Mises应力最大值为583 MPa，略大于接触应力最大值，但都低于材料的屈服强度，故螺纹段并没有产生塑性变形，避免了接头在上扣过程中的粘结损伤。

2.2 轴向拉伸载荷下连接安全性分析

接头上扣后，沿轴向对接头分别施加600，1 032 kN的拉伸载荷，得到螺纹最大应力分布和位移分布的变化曲线，如图6-7所示。

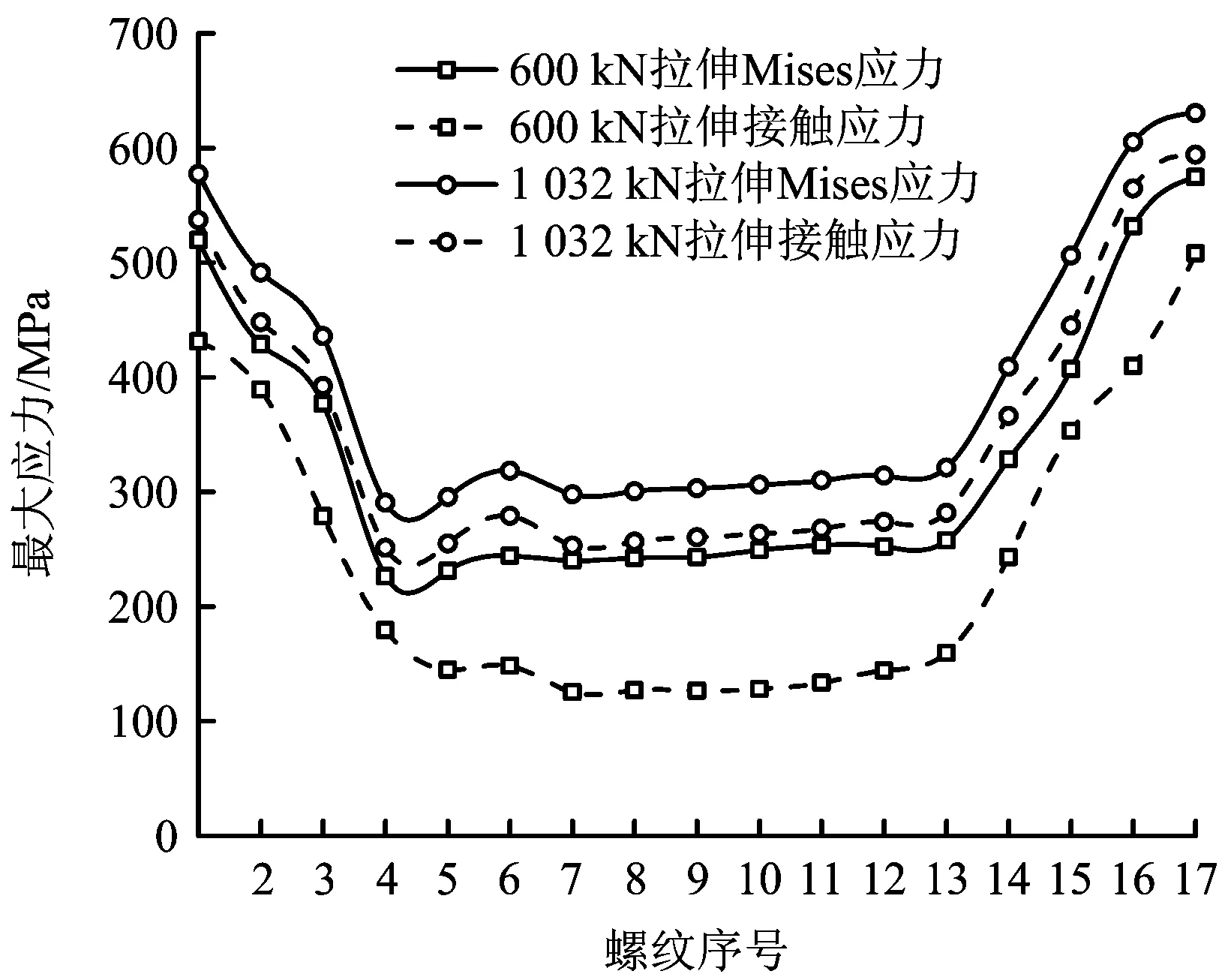
图6 拉伸载荷下螺纹最大应力分布Fig.6 The maximum stress distribution of the threads under tensile load

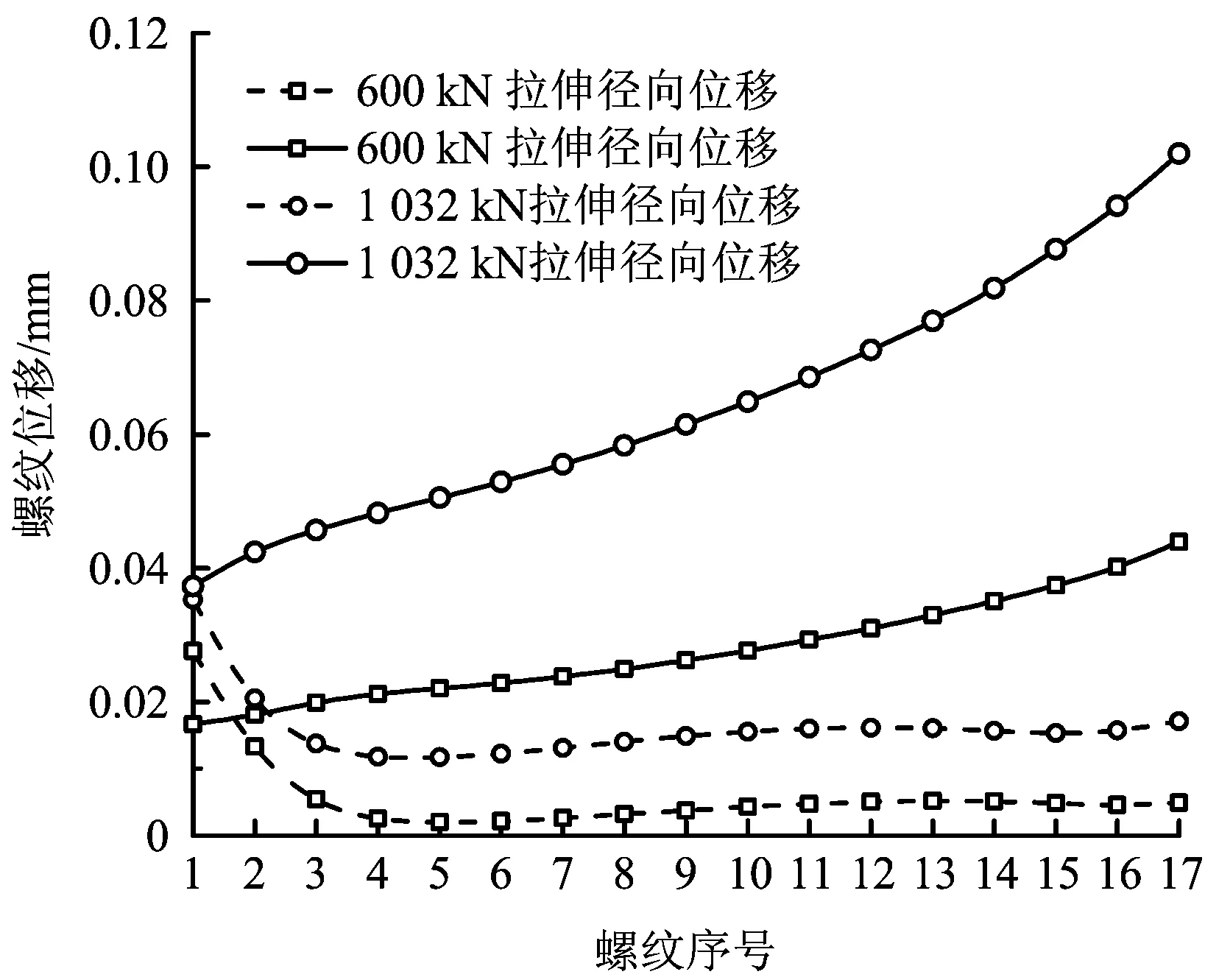
图7 拉伸载荷下螺纹位移分布Fig.7 The distribution of thread displacement under tensile load

由图6可知，在拉伸载荷作用下，螺纹首尾3扣应力值较大，中间段应力较小，螺纹应力分布整体表现为先急剧减小，后趋于平缓，最后迅速增加的趋势。在1 032 kN的极限拉伸载荷下，公扣大端的最后1扣最大Mises应力达到630 MPa，最大接触应力达到594 MPa，螺纹最后1扣产生屈服，但螺纹整体应力低于抗拉强度，不会出现断扣失效。

由图7可知，径向位移最大值出现在1号扣，径向位移变化规律是先逐渐降低然后缓慢增加接着又逐渐降低，最后逐渐增加；轴向位移则呈现单调增加的趋势，最大值出现在螺纹最后1扣。在1 034 kN拉伸载荷下，螺纹的最大径向位移为0.035 mm，最大轴向位移为0.1 mm，螺纹变形以为轴向为主，径向变形较小，接头发生滑脱可能性较低。

2.3 轴向压缩下连接安全性分析

对接头分别施加600，861 kN的轴向压缩载荷，得到了螺纹最大应力分布曲线及位移分布曲线，如图8-9所示。

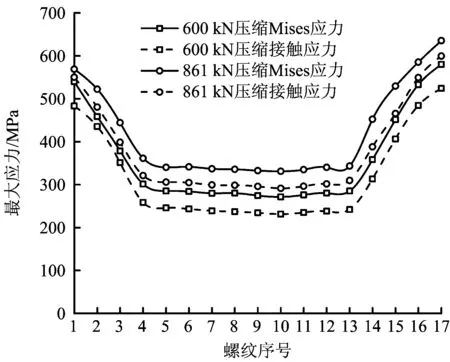
图8 压缩载荷下螺纹最大应力分布Fig.8 The maximum stress distribution of the threads under compressive load

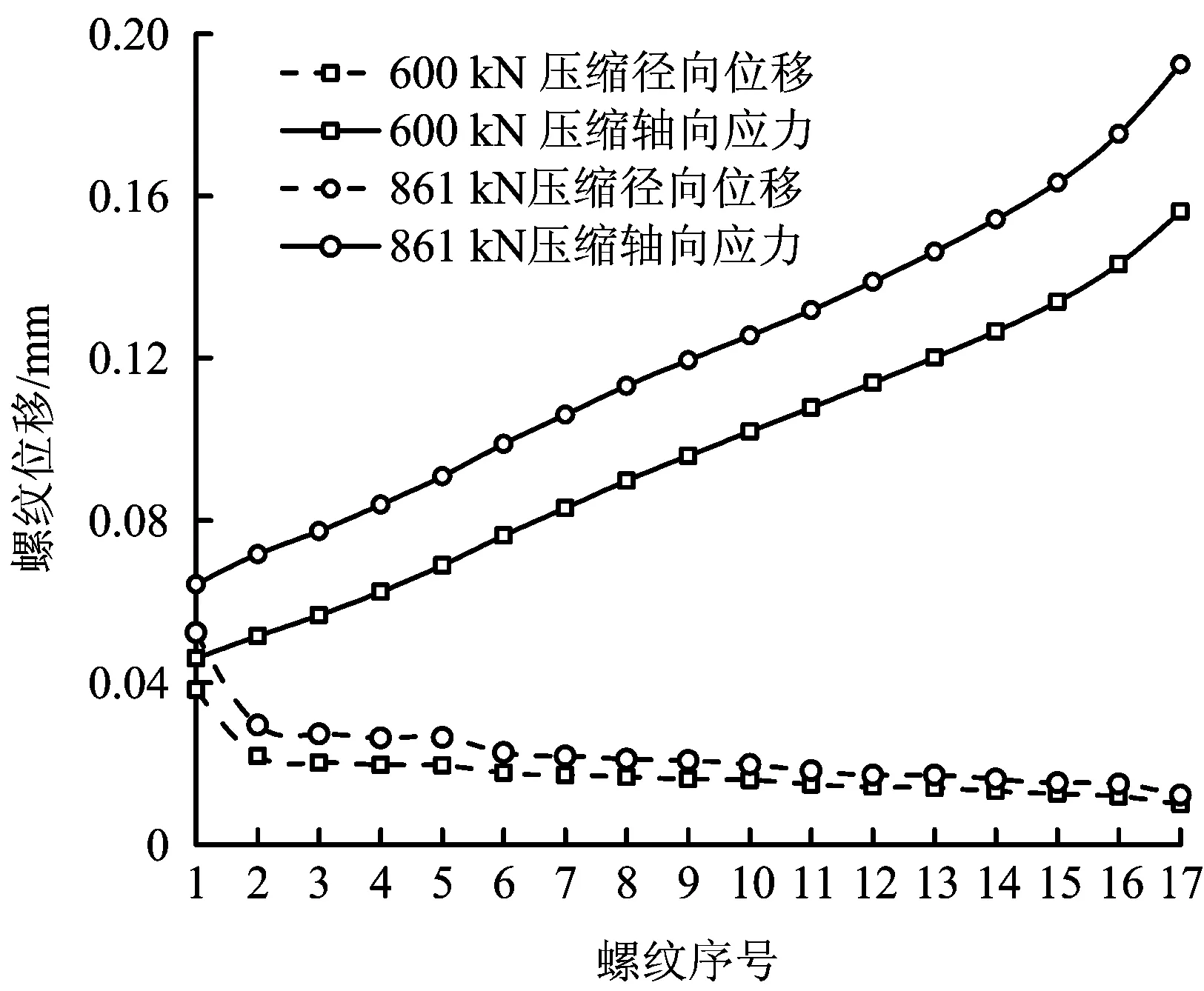
图9 压缩载荷下螺纹位移分布Fig.9 The distribution of thread displacement under compressive load

由图8可知，在压缩载荷作用下，螺纹应力分布曲线呈现两端高中间低的凹槽形，最大Mises应力及接触应力均出现在螺纹最后1扣，且螺纹首尾3扣依然具有明显的应力集中。在861 kN的极限压缩载荷下，螺纹第17扣应力最大，最大Mises应力达到635 MPa，最大接触应力为599 MPa，螺纹最后1扣产生屈服，但其他扣应力值均未超过屈服强度，连接可靠性高。

由图9可知，在压缩载荷下，螺纹的径向位移最大值出现在第1扣，径向位移分布规律是先急剧减小后缓慢减小，轴向位移则依然呈现单调增加的趋势，最大的轴向位移出现在螺纹最后1扣。在极限压缩载荷下，螺纹的位移以轴向位移为主，最大轴向位移为0.19 mm，接头发生脱扣可能性较低。

2.4 轴向拉伸和内压共同作用下连接安全性分析

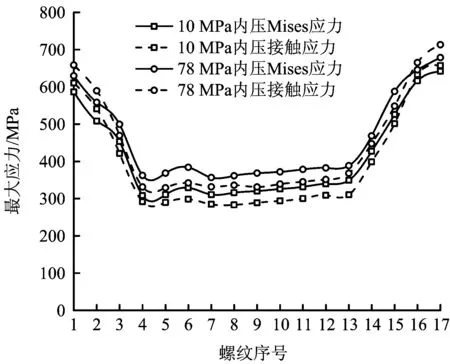
图10 拉伸载荷和内压作用下螺纹最大应力分布Fig.10 The maximum stress distribution of the threads under tension load and internal pressure

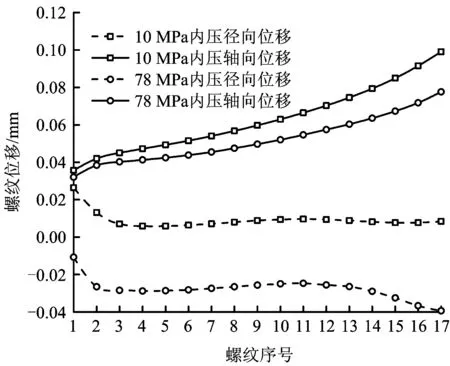
图11 拉伸载荷和内压作用下螺纹位移分布Fig.11 The distribution of thread displacement under tension load and internal pressure

对接头施加1 034 kN的轴向拉力，然后在接头内表面分别施加10 MPa和78 MPa的压力，得到了接头螺纹最大应力分布曲线及位移分布曲线，如图10-11所示，同时得到了台肩及密封面应力分布曲线，如图12-14所示。

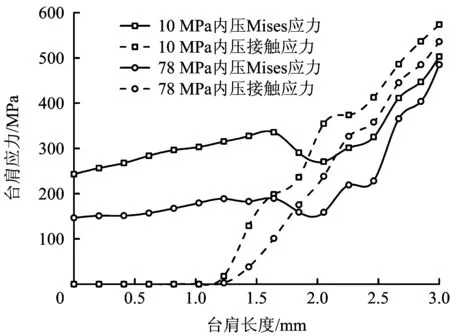
图12 拉伸载荷和内压作用下台肩应力分布Fig.12 Stress distribution of the shoulder under tension load and internal pressure

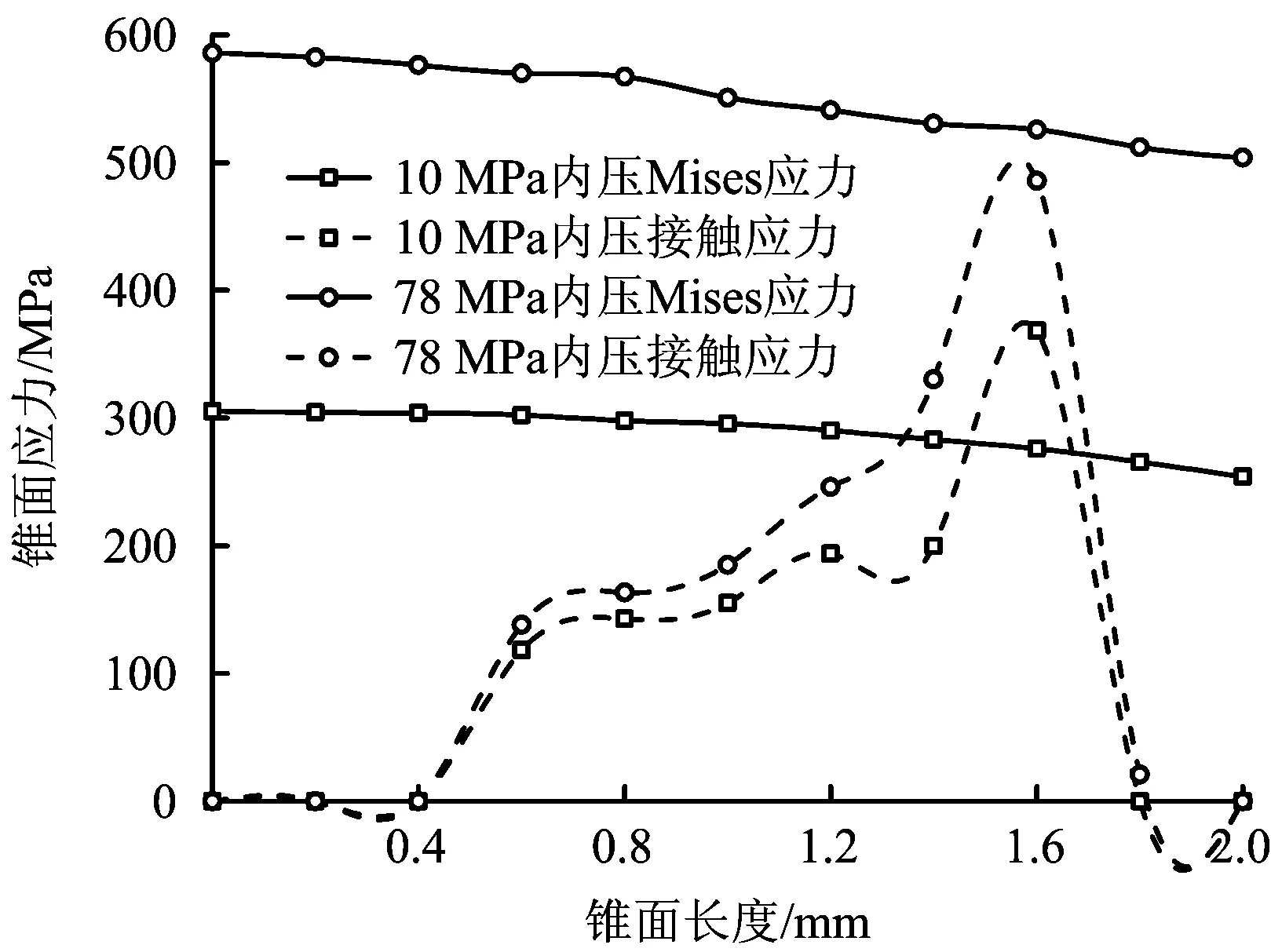
图13 拉伸载荷和内压作用下锥面应力分布Fig.13 Stress distribution of the conical surface under tension load and internal pressure

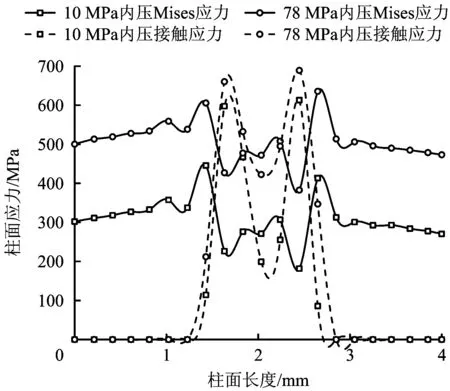
图14 拉伸载荷和内压作用下柱面应力分布Fig.14 Stress distribution of the cylindrical surface under tension load and internal pressure

由图10可知，螺纹最大Mises应力和接触应力均随着内压的增加而增大，最大的应力出现在公扣大端最后1扣。在在极限拉伸和内压载荷共同作用下，螺纹第1扣和最后2扣的最大应力均超过材料的屈服极限，但未达到抗拉强度，螺纹可能发生粘扣但不会断扣。由图11可知，螺纹径向位移和轴向位移均随着内压的增加而减小，内压导致管体膨胀，与接箍螺纹连接更为紧密，螺纹脱扣可能性降低。

由图12可知，台肩面的应力值及接触长度随着内压的增加而减小，在极限拉伸和内压载荷下，台肩零接触应力长度扩展到1.25 mm，但是接触应力值大于78 MPa的接触长度依然有1.4 mm，辅助密封效果明显。由图13-14可知，锥面和柱面的接触应力值及接触长度随着内压的增加有不同程度的增加，在极限拉伸和内压下，锥面和柱面接触应力和接触长度较大，密封性能可靠，且密封面Mises应力并未超过材料的屈服极限，密封面不会出现屈服失效。

2.5 轴向拉伸和内外压共同作用下连接安全性分析

对接头施加1 032 KN轴向拉伸载荷和10 MPa的内压，然后在接头外表面分别施加10 MPa和83 MPa的外压，得出接头螺纹最大应力分布曲线及位移分布曲线，如图15-16所示，同时得到了扭矩台肩及密封面应力分布曲线，如图17-19所示。

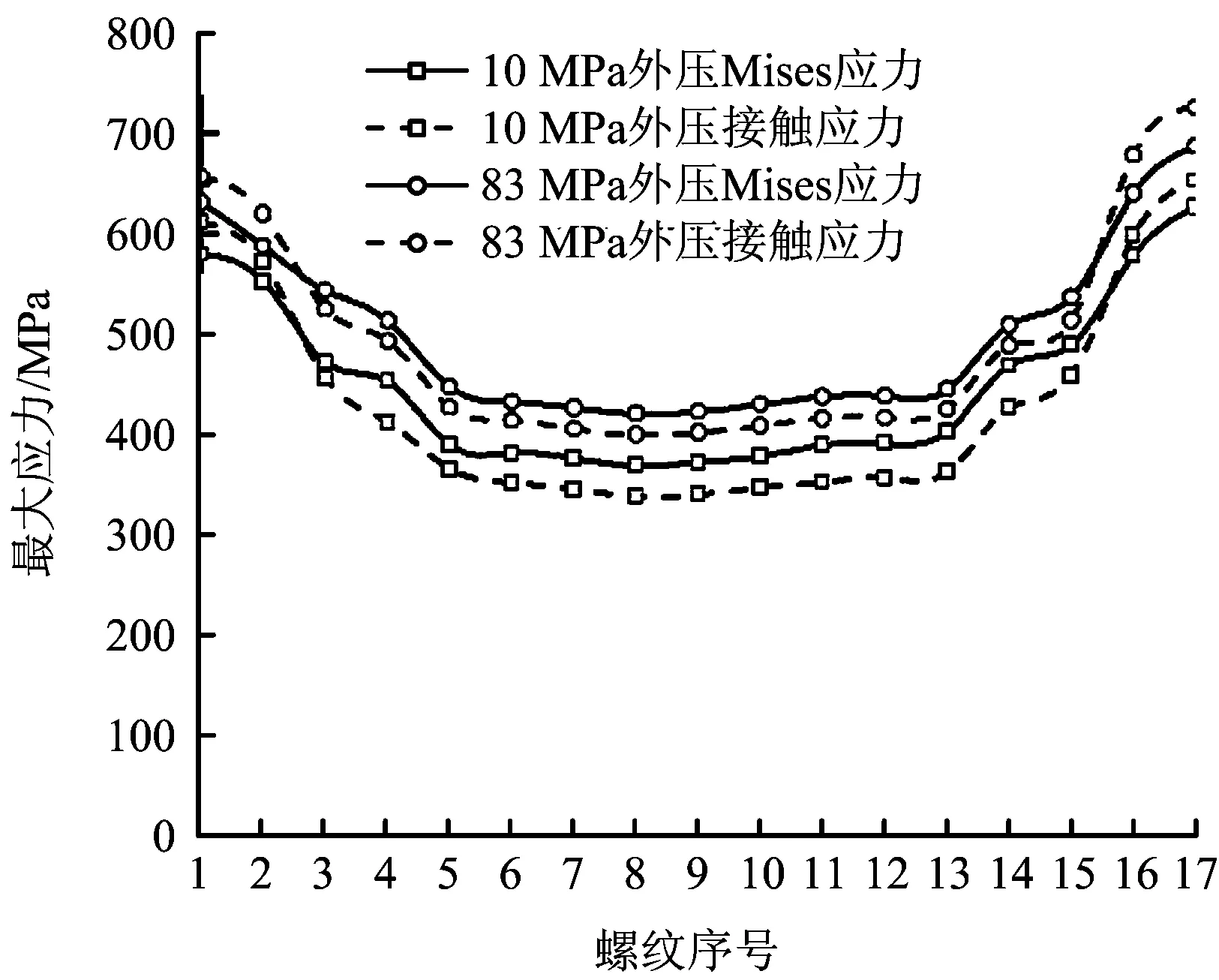
图15 拉伸载荷和内外压作用下螺纹最大应力分布Fig.15 The maximum stress distribution of the threads under tension load, internaland external pressure

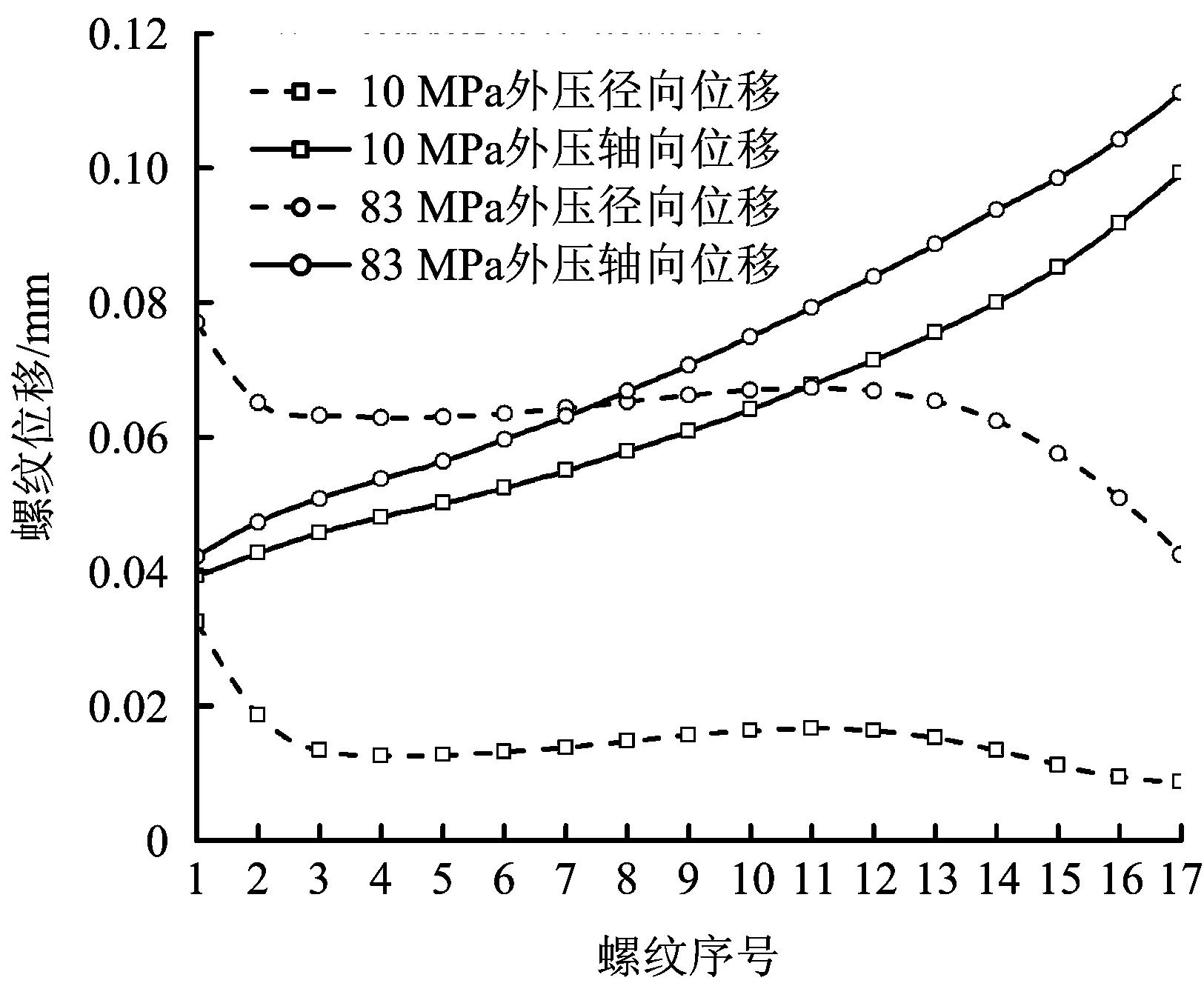
图16 拉伸载荷和内外压作用下螺纹位移分布Fig.16 The distribution of thread displacement under tension load, internal and external pressure

由图15可知，在拉伸载荷和内外压共同作用下，接头螺纹的最大应力随着外压的增加而增大，中间段螺纹应力分布均匀，螺纹首尾3扣应力存在明显的应力集中。在83 MPa极限外压作用下，螺纹首尾2扣最大应力已经超过材料的屈服极限。由图16可知，螺纹径向位移和轴向位移随外压增加而增大，在83 MPa的极限外压下，螺纹最大径向位移为0.077 mm，最大轴向位移为0.111 mm，变形主要以轴向位移为主，螺纹发生脱扣可能性很低。

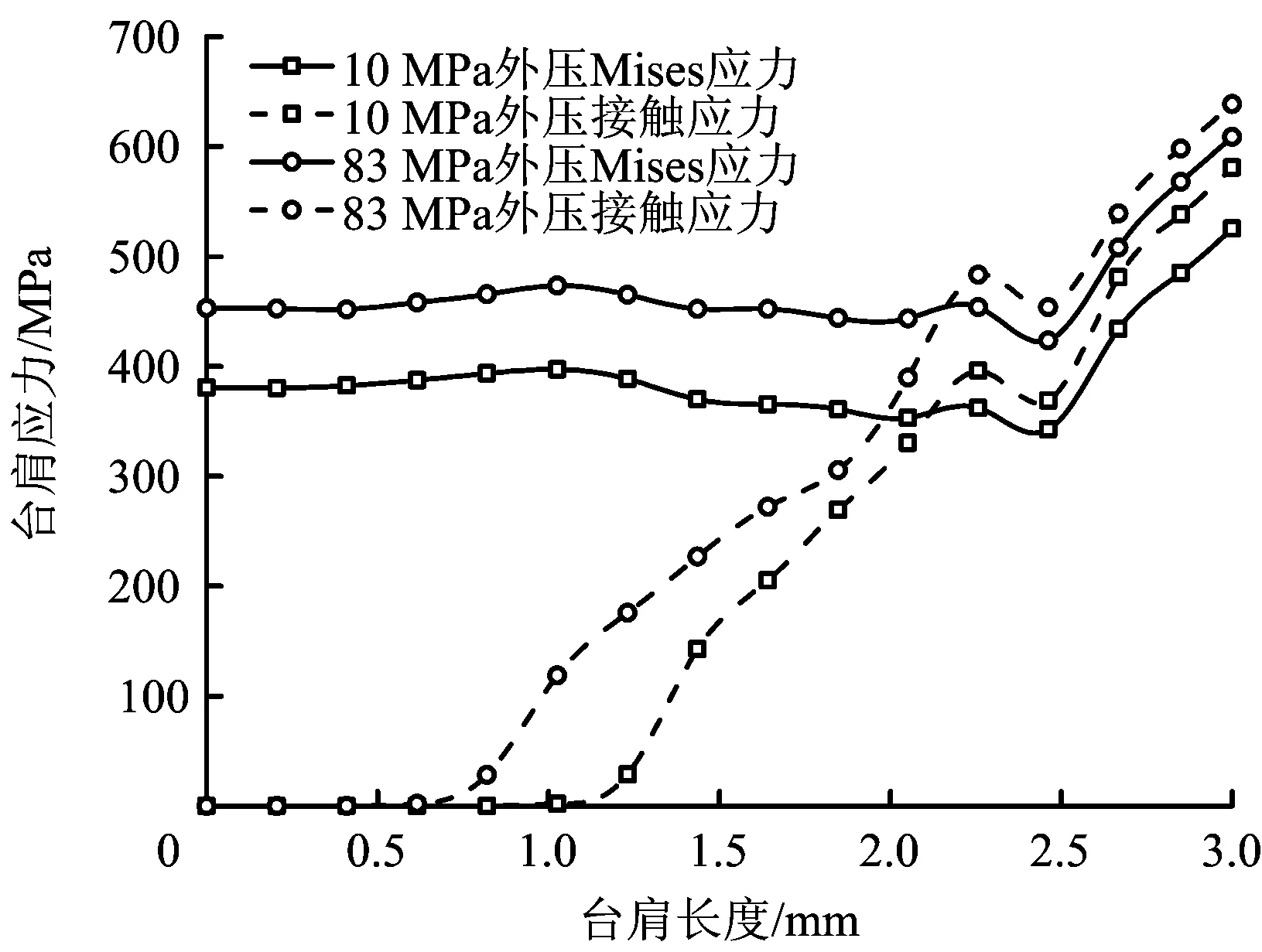
图17 拉伸载荷和内外压作用下台肩应力分布Fig.17 Stress distribution of the shoulder under tension load, internal and external pressure

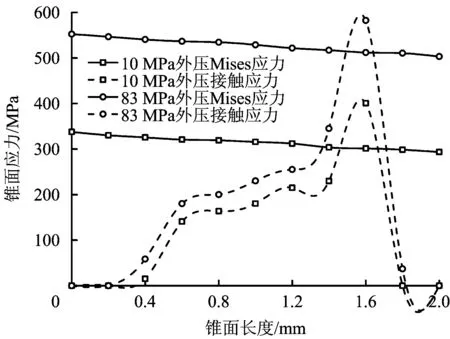
图18 拉伸载荷和内外压作用下锥面应力分布Fig.18 Stress distribution of the conical surface under tension load, internal and external pressure

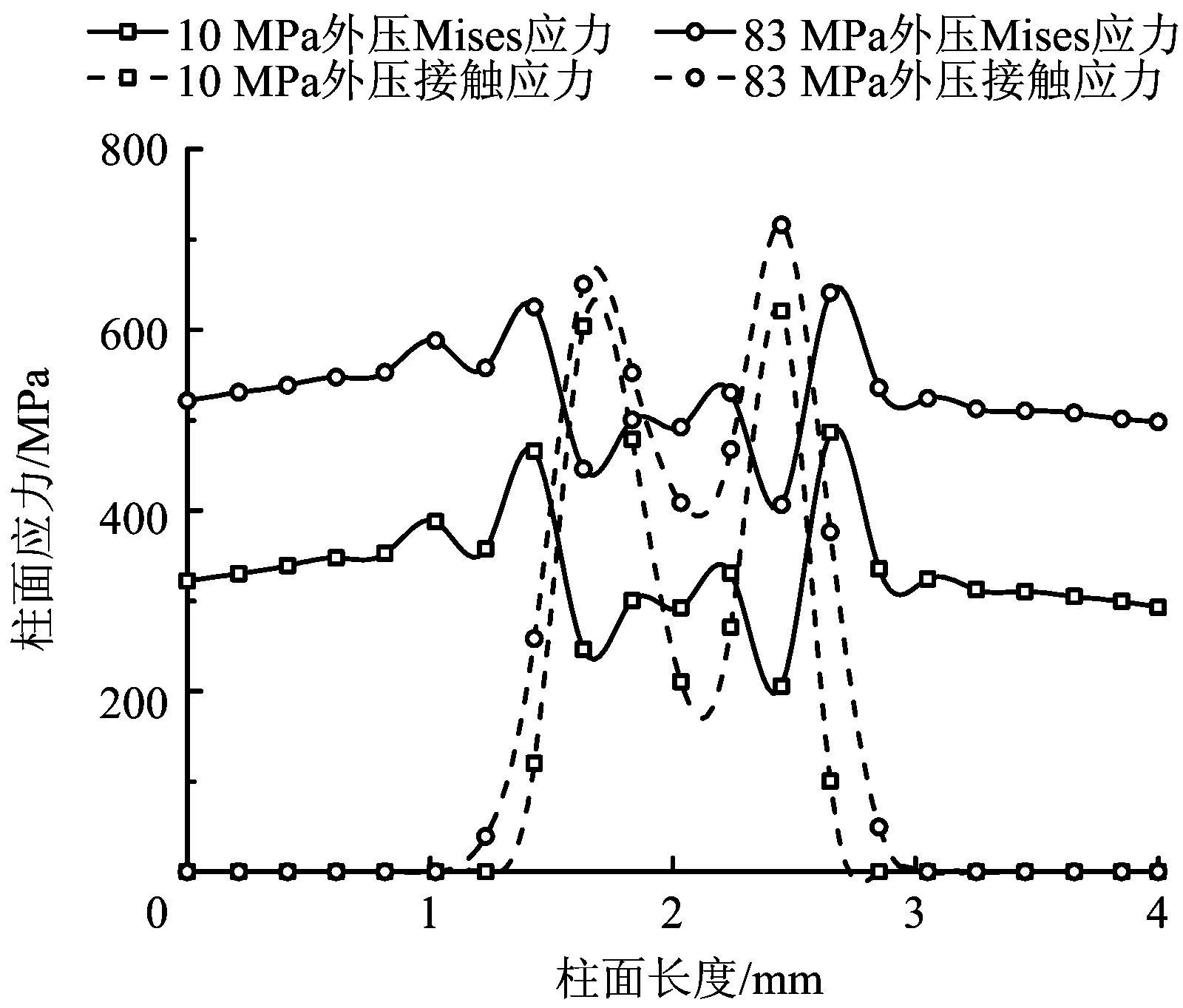
图19 拉伸载荷和内外压作用下柱面应力分布Fig.19 Stress distribution of the cylindrical surface under tension load, internal and external pressure

由图17可知，台肩面的应力值及接触长度随着外压的增加而增加，极限外压下，台肩面接触应力值大于78 MPa的接触长度有1.7 mm，辅助密封效果明显。由图18和图19可知，锥面和柱面的接触应力值及接触长度随着外压的增加有不同程度的增加，在极限拉伸和外压下，锥面和柱面接触应力和接触长度较大，密封性能可靠，且锥面Mises应力未超过材料的屈服极限，柱面上仅有局部Mises应力超过材料的屈服极限，综合来看，密封面具有良好的密封可靠性。

3 全尺寸试验

利用数控机床，加工出该特殊螺纹，并对螺纹段进行QPQ表面处理，随机选择3根接头试样进行试验，试验按API RP 5C5标准[16]进行。试验内容主要包括：螺纹参数检验、上卸扣试验、连接强度试验、气密封试验。将接头在液压大钳上进行10次循环上卸扣，然后对接头进行极限拉伸和压缩试验，最后对接头进行极限内外压气密封试验。上卸扣试验装置、连接强度试验装置以及气密封试验现场如图20所示。

图20 试验装置Fig.20 Experimental equipment

试验结果表明，该接头在上卸扣过程中并未出现粘结现象，在极限拉伸和压缩载荷下，管体出现屈服，接头螺纹并未出现滑脱和断扣，试验后3根接头公扣的形貌如图21所示。在内外压气密封试验中，从控制室计算机面板上未观察到接头出气口出现泄漏气泡，稳压期间传感器也未检测到压力波动，接头气密封性能良好。

图21 试验后试样形貌Fig.21 The morphology of samples after testing

全尺寸试验较好地验证了有限元的分析结果，该接头具有良好的连接安全性。目前该特殊螺纹接头处于试验研发阶段，技术成熟后便会投入到油气井中使用。

4 结论

1)在5种典型工况下，特殊螺纹接触应力及Mises应力呈现出两端高中间低的凹槽形分布规律，螺纹首尾3扣应力值较大，该部位是连接性能的薄弱区。特殊螺纹径向位移最大值出现在公扣的起始螺纹处，轴向位移最大值出现在公扣最后1扣牙，滑脱失效首先发生在首尾起始螺纹段。

2)特殊螺纹连接性能受外部载荷的影响较大。螺纹最大应力值随拉伸、压缩、内压及外压载荷的增加而增大，螺纹首尾起始扣牙应力增大较明显，易屈服失效。特殊螺纹径向位移及轴向位移随拉伸、压缩、外压载荷的增加而增大，随内压载荷的增加而减小。在一定程度上，内压载荷的作用降低了螺纹滑脱的可能性。

3)全尺寸试验及有限元分析综合表明，该特殊螺纹接头上卸扣性能满足使用要求；在极限轴向载荷下，管体屈服，但接头并未发生脱扣或断扣现象，连接强度较高；在内外压气密封试验中，接头并未出现泄漏，密封性能良好。接头脱扣及泄漏发生在管体屈服之后，这一特性有利于保障油气井的安全。

[1] 蔡晓闻, 高连新.我国油套管特殊螺纹接头的发展现状[J]. 焊管, 2008, 31(4):41-44.

CAI Xiaowen, GAO Lianxin. Current development situation of the special thread connection for tubing/casing[J]. Welded Pipe and Tube, 2008, 31(4): 41-44.

[2] 黄强. 油管螺纹损坏原因与对策[J]. 石油天然气学报, 2005, 27(4):708-717.

HUANG Qiang. The damage causes of tubing thread and countermeasures[J].Journal of Oil and Gas Technology, 2005, 27(4): 708-717.

[3] 袁光杰, 林元华, 姚振强, 等. API偏梯形套管螺纹连接的接触应力场研究[J]. 钢铁, 2004, 39(9):35-38.

YUAN Guangjie, LIN Yuanhua, YAO Zhenqiang, et al. Research on contact stress field of API buttress casing thread connection[J]. Iron and Steel, 2004, 39(9):35-38.

[4] Takano J, Yamaguchi M, Kunishige H. Development of premium connection “KSBEAR” for withstanding high compression, high external pressure, and severe bending [J]. Kawasaki steel technical report, 2002(47):14-22.

[5] 陈守俊, 高连新, 张毅, 等. 油套管螺纹联接粘扣失效过程的试验研究[J]. 华东理工大学学报(自然科学版), 2012, 38(2):247-251.

CHEN Shoujun, GAO Lianxin, ZHANG Yi, et al. Experimental study of galling failure process in oil pipe threaded connection [J]. Journal of East China University of Science and Technology (Natural Science Edition), 2012, 38(2): 247-251.

[6] 袁光杰, 姚振强. 油套管螺纹连接抗粘扣技术的研究现状及展望[J]. 钢铁, 2003, 38(11):66-69,14.

YUAN Guangjie, YAO Zhenqiang. Recent situation and future of anti-galling technique for API round thread [J]. Iron and Steel, 2003, 38(11): 66-69,14.

[7] PAN Z Y, SONG S Y, LIU W H, et al. Cause analysis of buttress premium thread connection pullout for a well [J]. Advanced Materials Research, 2011, 37:627-632.

[8] 王琍, 陈兆能, 佟德纯, 等. 套管接头螺纹滑脱失效有限元分析[J]. 北京科技大学学报, 2001, 23(2):137-139.

WANG Li, CHEN Zhaoneng, TONG Dechun, et al. Finite element method simulation of failure on casing thread connection [J]. Journal of University of Science and Technology Beijing, 2001, 23(2): 137-139.

[9] 陈祖志, 宋占兵, 石坤, 等.储气井螺纹连接安全性有限元模拟分析及实验研究[J]. 中国安全生产科学技术, 2012, 8(10):58-63.

CHEN Zuzhi, SONG Zhanbing, SHI Kun，et al. Experimental study and finite element simulation on safety performance of gas storage well’s thread joint [J]. Journal of Safety Science and Technology, 2012, 8(10): 58-62.

[10] 周星. 石油套管螺纹连接性能仿真分析[D]. 东营: 中国石油大学(华东), 2009.

[11] 高连新. 石油套管特殊螺纹接头的结构与性能研究[D].上海: 上海交通大学, 2005.

[12] American Petroleum Institute. Specification for threading, gauging, and thread inspection of casing, tubing, and line pipe threads: API SPEC 5B-2008[S]. Washington DC: API, 2008.

[13] Hua Z. Analysis of the load distribution in a bolt-nut connector[J]. Computers & Structures, 1994, 53(6):1465-1472.

[14] 齐俊林, 罗维东, 张宏, 等.圆螺纹套管接头上扣滑脱与数值模拟[J].石油大学学报(自然科学版), 1998, 22(4):68-71.

QI Junlin, LUO Weidong, ZHANG Hong, et al. Numerical Simulation of screw-on and jump-out behavior of threaded casing connections[J]. Journal of the university of petroleum china (Edition of natural science), 1998, 22(4): 68-71.

[15] Rabia H. 套管设计基础[M].华仲箎译. 北京：石油工业出版社，1995.

[16] American Petroleum Institute. Recommended practice for evaluation procedures for casing and tubing connections: API RP 5C5-2003[S]. Washington DC: API, 2003.