基于Weibull分布的煤体强度计算研究*

陈学华，吕鹏飞，宋卫华，周年韬

(辽宁工程技术大学 矿业学院，辽宁 阜新 123000)

0　引言

地下工程研究的数百年里，煤岩体强度一直是个备受关注的科学问题[1-2]。由于地下工程所处地理环境的恶劣，很难实地进行准确的强度测试，多数采用现场取样，在实验室加工试件并进行强度测试的方法，但是实验室的测试结果又与实际强度存在一定差异，根据实验室测试强度大体估算煤岩体真实强度存在较大误差；另一方面，煤岩体真实强度在矿山压力计算和数值模拟等当中又被经常使用，因此，有必要寻求一种理论上可行，操作上简便，准确性也较高的方法来合理地计算出煤体强度。

专家学者几十年来从未间断过对于煤体强度的研究。石永奎[3]、林琼[4]等对不同直径和高度的煤和灰岩试件进行了强度测试，采用实验方法证明了煤岩强度具有相应的尺寸效应；傅雪海[5]、张鹏[6]、朱传奇[7]、高霞[8]等采用岩石力学实验方法研究了气水饱和、干湿循环、含水率和孔隙率、含瓦斯水合物煤体的强度特征，结果表明煤体中杂质的生成促使煤体容易发生破坏，降低其强度；李凤颖[9]采用PFC软件模拟分析了煤体离散性特征及其对强度的影响；彭瑞[10]等针对Hoek-Brown强度准则复杂的地质参数，建立Hoek-Brown参数与煤岩地质力学参数之间新的转换关系，提出岩体强度参数的新解；李忠华[11-13]等发明了钻杆扭矩法，可实现在地下直接测试煤岩体强度，为地下岩体强度直接测试提供新思路。上述研究众多，实验室实验不能消除煤岩试件强度与现场煤体强度间的误差，现场测试操作繁杂且人员操作误差较大，数值模拟和理论推导存在一定理想性。所以笔者在借鉴上述研究的同时，采用理论分析、实验室实验、数值模拟、拟合分析等手段综合研究出一种煤体强度的理论计算方法和计算公式，为现场煤体强度的研究提供新思路。

1　煤样单向抗压强度尺寸效应实验结果

采集并可供分析的单向抗压强度尺寸效应实验的煤样共3份，其中兖州矿区东滩煤矿3上煤1份，平顶山六矿丁煤1份，借用国外研究结果1份[14]。国内煤样均制成立方体，每份煤样中含有的尺寸分别为边长25,50,100,150,200 mm共5组，每组3个煤样，共实验了10组30个煤样，借用国外5组15个煤样。不同尺寸的各组煤样单向抗压强度均值结果如表1所示。图1为文献[15]提出的指数函数煤体强度拟合形式所对应的3份煤样的实验拟合结果。当煤样尺寸D很小(取D=1 mm)时，可以认为其中不包含任何天然缺陷，则此时的煤样强度定义为原煤强度σ0，按照图1中的拟合公式计算得出Bieniawski煤矿、平顶山丁煤、兖州3上煤的σ0分别为38.85,31.58,29.98 MPa。

表1　煤样单向抗压强度尺寸效应实验结果

图1　煤样抗压强度尺寸效应拟合结果Fig.1　Fitting results of size effect on compressive strength of coal sample

2　基于Weibull分布的煤样单向抗压强度

煤体试件强度的离散性特征和尺寸效应特征是材料内部不同尺度且杂乱无章的细观缺陷所经历演化的必然结果，为了较好地处理无规则试件，比较有效手段就是概率统计方法，因此可以采用概率统计中的Weibull分布方法分析微观煤体强度与宏观煤体强度的关系。若将煤体试件的一个常规截面划分成若干基元，其强度用Weibull统计函数描述，则煤体试件的宏观强度可由Weibull分布中的参数σ0和m近似，σ0为基元体强度的平均值，称为尺度参数，也就是对应前面所述的原煤强度；m为函数形状参数，称为均质度。均质度的物理意义可表示为煤样中缺陷分布不规则程度的度量，假如煤体裂纹表示煤体缺陷，则其表征为煤体裂纹的分布、位置以及粗糙度等对煤体强度的影响。煤体试件的均质度越大，其基元的裂隙化程度就越低，当均值度趋于无穷大时，可将煤体试件看成无缺陷，其基元强度趋近于同一数值，这一数值即是煤体试件的宏观强度。综合以上分析可得出，当m值非常大(m>100)时，煤样的宏观强度就是细观上无缺陷的均质材料强度，将其称作原煤强度σ0，这一点与weibull函数中的基元强度相对应，所以用同一字母表示；反之，当m值减小时，基元的裂隙化程度就会提高，当m趋近于0时，煤样宏观强度就取决于缺陷基元的强度。因此，m值很小(m=1.5)时的煤样宏观强度就是细观上缺陷起主导作用的均质性极差材料的强度，将其称作煤体强度σm。煤样的实验强度则介于以上2种强度之间，其数值受Weibull分布的2个参数的影响，也就是说煤质组分和缺陷共同控制煤样强度。

利用RFPA软件的Monte-carb功能和Weibull函数对表1强度测试结果进行模拟计算，求解6种不同尺寸(包括D=1 mm)的试件对应强度值的均质度，数值计算时将试件模型划分为10 000个网格单元，其他试件参数以现场实测数据为准，多次输入不同m值，直到模拟强度值与实验强度值相差小于1%，然后记录下此时的m值数据，表2为表1所对应强度的均质度模拟计算结果。综合表1、表2可以看出，同一煤矿的煤样其单向抗压强度会随试件尺寸增加而减小，随试件均质度减小而减小；对于均质度相近的不同矿区煤样，其原煤强度越小，试件单向抗压强度也越小。

表2　煤样均质度数值计算结果

为了探求出煤体试件强度σc和原煤强度σ0之间关于均质度m的函数关系，继续利用RFPA软件对现场实际条件中的不同σ0和m值进行组合数值模拟，测试其单向抗压强度，将每个模型都划分5 000个单元，在y方向施加垂直载荷，煤体试件的单向抗压强度数值计算结果如表3所示。

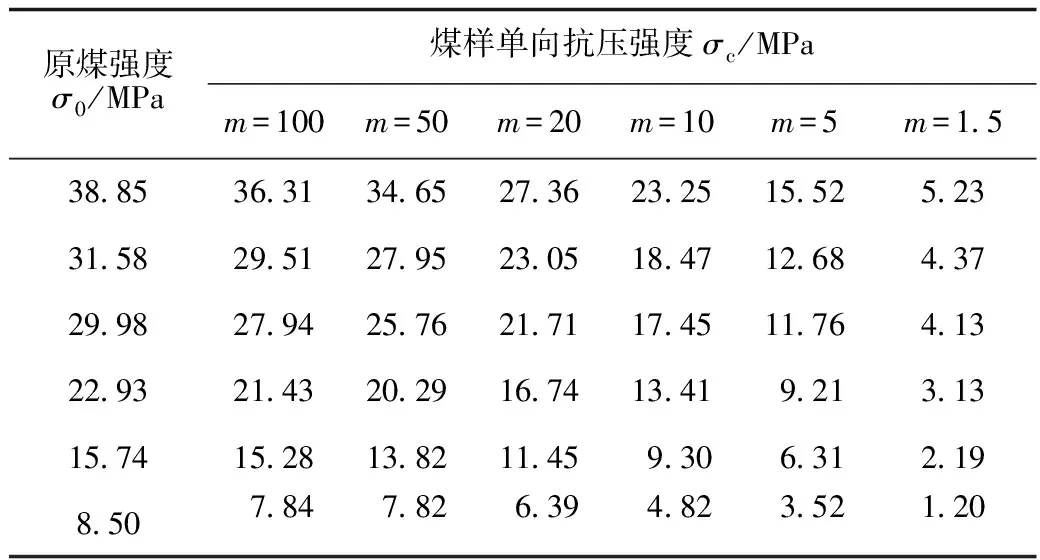
表3　煤样单向抗压强度数值实验结果

从每一行数据可以看出，煤体强度会随m值的减小而减小；从每一列数据可以看出，煤体试件强度会随原煤强度σ0的减小而减小。任意两行及两列数据的σc与σ0的比值相等，这说明以上的2个规律是独立存在的，不同的煤种其强度会随着m值变化的衰减规律具有同一性，而当均质度相同时，不同原煤强度的煤样会具有同一衰减规律。

若定义同种煤的煤样强度σc与原煤强度σ0之比为均质度影响系数Km，通过对表3各行数值的拟合分析，得到均质度与其影响系数Km之间关系如图2所示，图2中的回归精度分别为当m<10时，回归方差R2为0.921 8，当m≥10时，回归方差R2为0.947 7，得到其回归公式见式(1)。

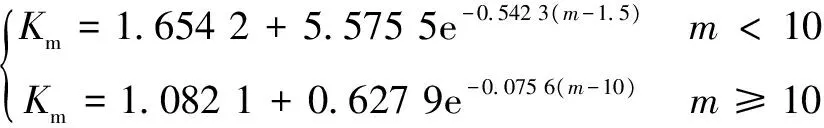
(1)

式中：m为均质度。

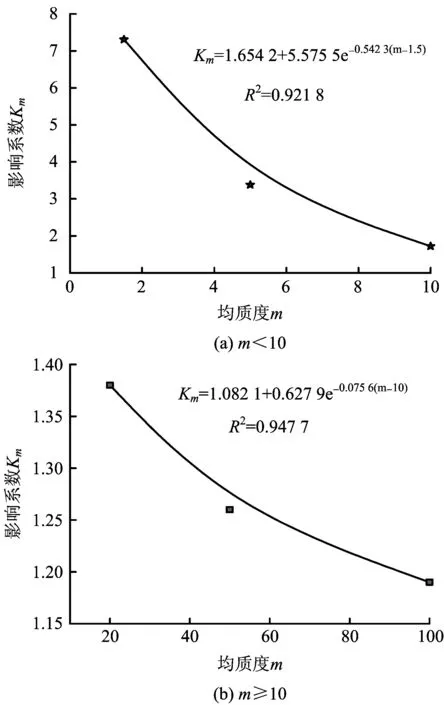
图2　均质度影响系数回归曲线Fig.2　Influence coefficient of homogeneity curves

若定义均质度相同的不同煤种试件强度及原煤强度与标准煤样的试件强度及原煤强度之比为原煤强度影响系数K0，标准煤样是指边长为50 mm的煤样，则通过对表3各列数值的拟合分析，得到回归公式见式(2)，回归精度为R2=0.936 9。

K0=0.949+3.541e-0.117 2(σ0-8.5)

(2)

式中：σ0为原煤强度/MPa。

则任意尺寸煤样的单向抗压强度σc为：

σc=38.85/k0km

(3)

3　煤体单向抗压强度计算

由于煤岩体的强度在矿山工程中很难进行原地的测试，然而矿山工程中的诸多数值计算或理论计算等在原则上又要采用煤体强度，为了解决这类问题，提出一种煤体单向抗压强度的计算新方法。首先定义标准煤样的强度为标准强度，记为σs。然后结合公式(1)～(3)对已经测试好标准强度的8组煤样对其原煤强度和煤体强度进行求解，经过计算得出其标准强度、原煤强度和煤体强度的结果，如表4所示。对表4中的数据进行再次的拟合分析，结果如图3和图4所示。

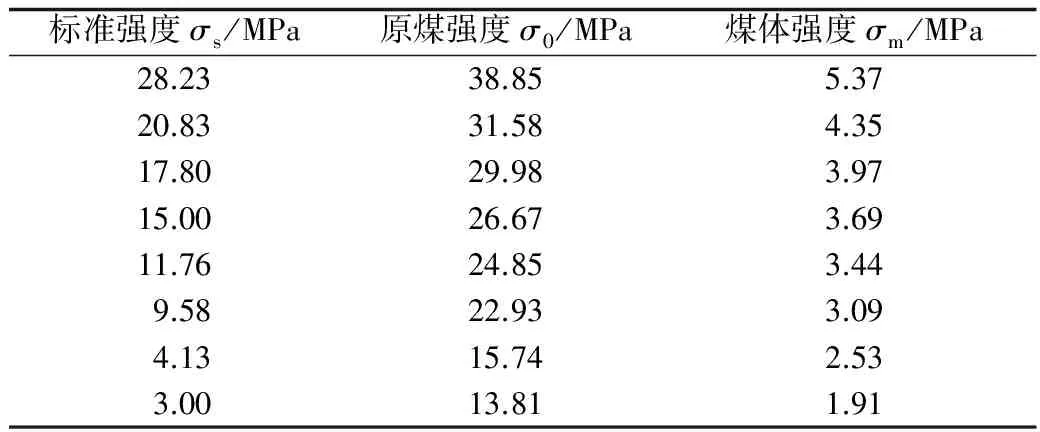
表4　煤样标准单向抗压强度与原煤强度及煤体强度对照Table 4　Comparison table between standard uniaxialcompressive strength of coal sample and raw coal strengthand strength of coal mass

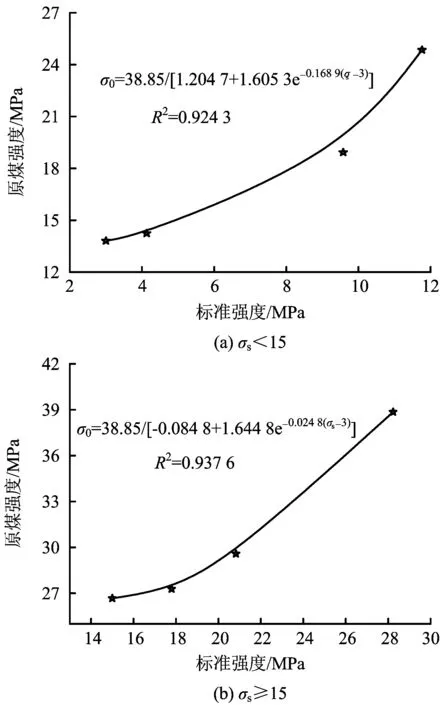
图3　标准强度与原煤强度回归曲线Fig.3　Regression curves of standard strength and raw coal strength

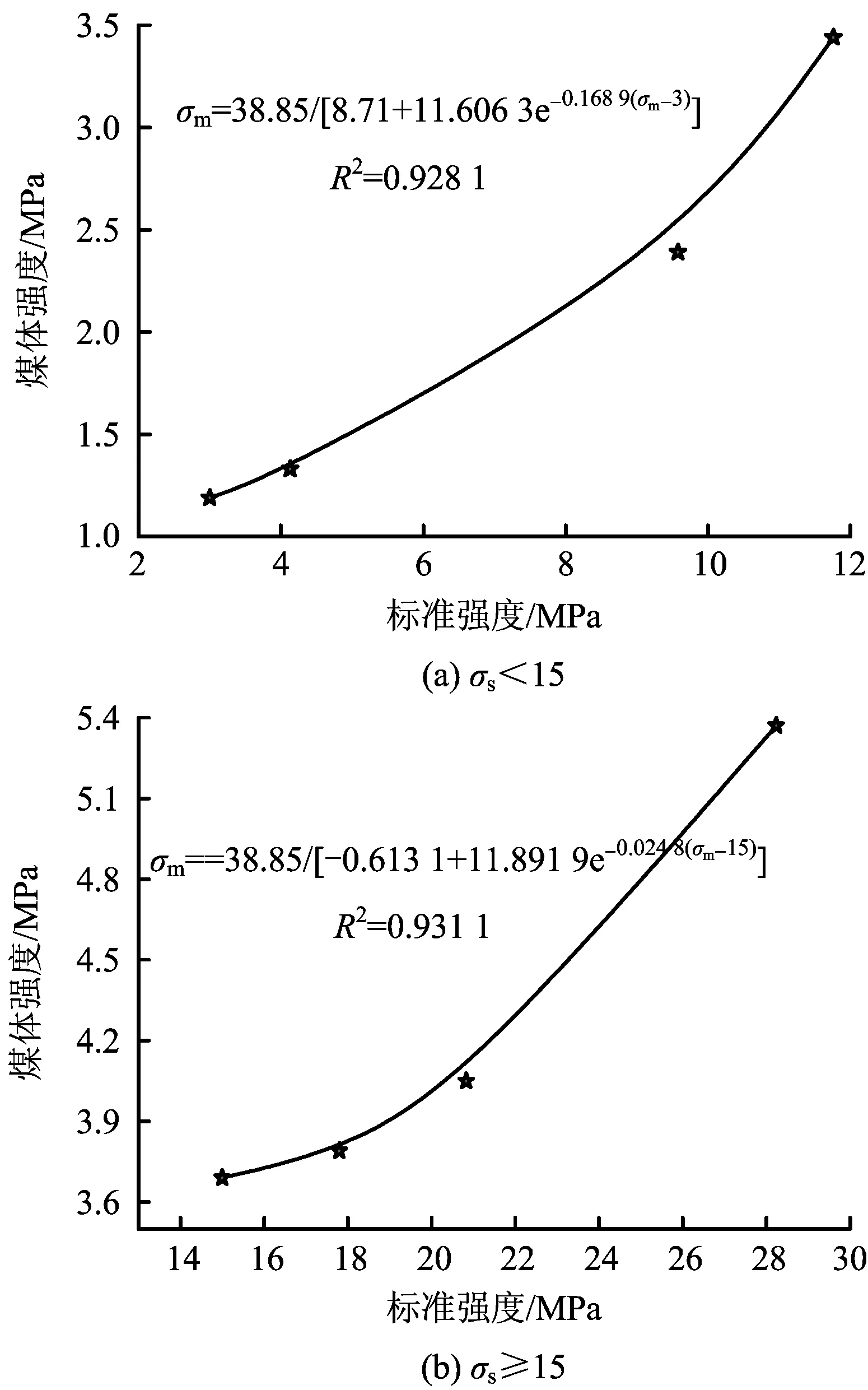
图4　标准强度与煤体强度回归曲线Fig.4　Regression curves of standard strength and coal strength

图3中的回归精度分别为当m<15时，回归方差R2为0.924 3，当m≥15时，回归方差R2为0.937 6；图4中的回归精度分别为当m<15时，回归方差R2为0.928 1，当m≥10时，回归方差R2为0.931 1。同时按照拟合结果得到原煤强度σ0、煤体强度σm、标准强度σs的回归关系见式(4)和(5)。其结果表明，当σs在3～28.23 MPa区间变化时，σm是σs的0.636 9～0.190 1倍。

(4)

式中：σs为标准单向抗压强度，MPa。

(5)

式中：σm为煤体单向抗压强度，MPa。

4　结论

1)煤体内部缺陷是导致其强度存在尺寸效应的根本原因，Weibull分布可较好的描述煤体宏观强度，Weibull函数中的均质度参数可对煤体内部缺陷进行度量，煤体宏观强度是原煤强度和均质度的函数，并且宏观强度随原煤强度和均质度降低呈现递减的规律。

2)按照煤样抗压强度尺寸实验结果，采用RFPA软件的Weibull函数功能，数值计算求解不同条件下的均质度值，据此拟合得出原煤强度、均质度、标准强度之间的函数关系，建立煤体强度计算的拟合公式。

[1]宋建波,张倬元,于远忠,等. 岩体经验强度准侧及其在地质工程中的应用[M]. 北京：地质出版社,2002.

[2]祁连光,杨科,陆伟,等. 煤系地层岩石单轴抗压强度统计分析[J]. 煤炭科学技术,2013,41(2):100-103.

QI Lianguang, YANG Ke, LU Wei, et al. Statistical analysis on uniaxial compressive strength of coal measures[J]. Coal Science and Technology,2013,41(2):100-103.

[3]石永奎,马源鸿,尹延春. 尺寸效应对煤层冲击倾向性测试结果的影响[J]. 煤炭科学技术,2014,42(2):23-26.

SHI Yongkui, MA Yuanhong, YIN Yanchun. Research on size effect affected to seam bump-prone test results[J]. Coal Science and Technology,2014,42(2):23-26.

[4]林琼,毕忠伟,梁政. 基于尺度效应的灰岩强度研究[J]. 中国安全生产科学技术,2007,3(1):26-30.

LIN Qiong, BI Zhongwei, LIANG Zheng. The study of size effect on the limestone strength[J]. Journal of Safety Science and Technology,2007,3(1):26-30.

[5]傅雪海,秦勇,姜波,等. 多相介质煤岩体力学实验研究[J]. 高校地质学报,2002,8(4):446-452.

FU Xuehai, QIN Yong, JIANG Bo, et al. Study on mechanics experiments of multiphase medium coal rocks[J]. Geological Journal of China Universities, 2002,8(4):446-452.

[6]张鹏,柴肇云. 干湿循环致砂岩单轴抗压强度弱化规律试验研究[J]. 煤炭科学技术,2016,44(S1):28-30+42.

ZHANG Peng, CHAI Zhaoyun. Study on deterioration rules of uniaxial compressive strength of sandstone during wetting-drying cycles[J]. Coal Science and Technology,2016,44(S1):28-30+42.

[7]朱传奇,谢广祥,王磊,等. 含水率及孔隙率对松软煤体强度特征影响的试验研究[J]. 采矿与安全工程学报,2017,34(3):601-607.

ZHU Chuanqi, XIE Guangxiang, WANG Lei, et al. Experimental study on the influence of moisture content and porosity on soft coal strength characteristics[J]. Journal of Mining & Safety Engineering,2017,34(3):601-607.

[8]高霞,刘文新,高橙,等. 含瓦斯水合物煤体强度特性三轴试验研究[J]. 煤炭学报,2015,40(12):2829-2835.

GAO Xia, LIU Wenxin, GAO Cheng, et al. Triaxial shear strength of methane hydrate-bearing coal[J]. Journal of China Coal Socety,2015,40(12):2829-2835.

[9]李凤颖. 煤岩力学性质的离散元数值模拟及应用探讨[D]. 成都：成都理工大学,2012.

[10]彭瑞,赵光明,孟祥瑞. 岩体强度参数新解及应用[J]. 中国安全生产科学技术,2014,10(5):43-48.

PENG Rui, ZHAO Guangming, MENG Xiangrui. Latest explanation of rock mass strength parameters and its application[J]. Journal of Safety Science and Technology,2014,10(5):43-48.

[11]朱丽媛,李忠华,徐连满. 钻屑扭矩法测定煤体应力与煤体强度研究[J]. 岩土工程学报,2014,36(11):2096-2102.

ZHU Liyuan, LI Zhonghua, XU Lianman. Measuring stress and strength of coal by drilling cutting torque method[J]. Chinese Journal of Geotechnical Engineering,2014,36(11):2096-2102.

[12]李忠华,朱丽媛,李国臻,等. 钻杆扭矩法测定煤岩强度的理论与试验研究[J]. 中国矿业大学学报,2015,44(4):612-616.

LI Zhonghua, ZHU Liyuan, LI Guozhen, et al. Experimental and theoretical study of determination of coal rock strength using the drill rod torque method[J]. Journal of China University of Mining Technology,2015,44(4):612-616.

[13]朱丽媛,李忠华,徐连满. 钻进速度对钻杆扭矩影响的理论分析与试验研究[J]. 实验力学,2015,30(3):395-400.

ZHU Liyuan, LI Zhonghua, XU Lianman. Theoretical analysis and experimental study of the influence of drilling rate on torque of drill rod[J]. Journal of Experimental Mechanics,2015,30(3):395-400.

[14]Bieniawski Z T. The effect of specimens size on compressive strength of coal[J]. International Journal of Rock Mechanics and Mining Sciences,1968(5):235-335.

[15]刘宝琛,张家生,杜奇中,等.岩石抗压强度的尺寸效应[J]. 岩石力学与工程学报,1998,17(6):611-614.

LIU Baochen, ZHANG Jiasheng, DU Qizhong, et al. A study of size effect for compression strength of rock[J]. Chinese Journal of Rock Mechanics and Engineering, 1998,17(6):611-614.