水毁灾害中埋地管道稳定性研究*

袁巍华，吴玉国，王国付，喻光安

(1.辽宁石油化工大学 研究生学院，辽宁 抚顺 113001；2.辽宁石油化工大学 石油天然气工程学院，辽宁 抚顺 113001； 3.武汉理工大学 材料科学与工程学院，湖北 武汉 430070)

0　引言

石油与天然气是当今社会发展的重要能源基础，埋地管道担负着我国油气资源的长输任务，有“国民经济动脉之称”[1]。

长输埋地油气管道铺设长度常常达到几百甚至上千公里，沿线地形、地质，气象情况变化莫测，加之管道建设工况复杂，工程施工难以避免穿越河流沟谷。因此，管道经常因洪水冲击、坡体滑动、冲沟、河床下切、河道摆动等导致管道整体变形、稳定性降低、裸露甚至悬跨漂浮，这些管道环境灾害统称为水毁灾害[2]。1994年5月[1]，长庆油田元-悦地区遭受70年一遇暴雨，直接导致埋地管道全线35%被冲毁，26处被拉断；2010年7月8日[3]，鄂西山区遭受强降雨，引发洪水造成忠武输气管道长距离漂管事故；2013年7月8日[4]，四川西北地区突降暴雨，导致兰成管道石亭江埋地穿越段于7月9日先是被洪水冲刷露管，随后穿越管段被冲断； 2016年11月13日，中缅天然气管道因连续强降雨造成龙陵1号隧道山体塌方，上游山体汇水直接顺管道顶部冲刷形成冲沟，对管道安全造成严重威胁。水毁灾害种类众多，形成因素复杂，覆盖范围广泛，造成的管道事故又非常容易引发次生灾害。据统计，在埋地管道环境地质灾害中，水毁灾害是造成经济损失最严重、对环境危害最深远的自然灾害之一[5]。

Bing Song等[6]分析了洪水和河床运动对管道的影响；张乐天等[7]分析了洪水冲击管道的流场分布和不同裸露情况下管道的力学反应；Gunnar Furnes等[8]研究了海洋中跨越管道的动态特性，并进行了实验验证；王晓霖等[9]基于解析方法编制了洪水管道分析程序，解析解与Abaqus有限元软件结果吻合良好，基于管道轴向应变，计算得到了管道在洪水中漂浮的极限长度；Sijia Li等[10]建立了管道与土壤耦合有限元模型，主要分析了缺陷对管道在水毁灾害中的影响；康习锋等人[11]考虑到管道初始缺陷，采用有限元方法对埋地管道屈曲临界载荷进行研究，得到屈曲临界载荷修正公式；谭东杰等[12]将微分求积法引入有限元软件进行运算，得到了洪水冲击下形成管跨的危险长度。

现有研究主要针对管道在水毁灾害中的应力分布情况，从材料强度角度分析水毁对管道的影响。本文采用有限元方法，考虑了不同管道外径和管道壁厚的影响，根据特征值屈曲理论，从结构角度分析了管道在水毁灾害中漂浮和悬跨2种主要形式下的稳定性，得到管道漂浮情况下的极限长度，结果与文献[9]一致。

1　研究方法

1.1　载荷计算

根据Morison[13]的理论，管道在水流中承受的载荷可以表示为：

(1)

(2)

(3)

(4)

(5)

式中：FD表示水流绕流拖拽力，N；D表示管道外径，m；V表示水流速度，m/s；FI表示水流惯性力，N；FL表示水流绕流升力，N；Ff表示浮力，N；W表示重力，N；ρp表示管壁密度，kg/m3；t表示管道壁厚，m；ρi表示管道内部介质密度，kg/m3；ρw表示水流密度，kg/m3，可以表示为：

ρw=ρo(1-Sv)+ρsSv

(6)

式中：ρo表示水与砂石密度和，kg/m3；ρs表示砂石密度，kg/m3；Sv表示单位体积水中含沙比，值取1.2%。

CD，CL，CM表示水动力系数，Morison公式属于经验公式，水动力系数需要通过实验来确定，本文采用《管道及储罐强度设计》[14]中给出的部分经验值。

表1　水动力系数经验值

根据Marston-Spangler[15]理论，管道在土壤中承受载荷可以表示为：

T=πDKη

(7)

(8)

G=CcρgghD

(9)

式中：T表示土壤与管道摩擦力，N；K表示土壤压力，N；η表示土壤与管道摩擦系数，本文认为回填土为沙土，沙土与管道摩擦系数一般取值为0.4～0.7，本文取0.5；ρg表示土壤密度，kg/m3；h表示管道埋深，m；φ表示土壤内摩擦角度，沙土内摩擦角一般在25～28°，本文取26°；G表示管土对管道压力，N；Cc表示填埋式土压力系数，根据Marston-Spangler理论一般取1.2～1.4，本文取1.3。

1.2　有限元模型

通过对比文献[1]和文献[3-12]中实际管道几何参数，定义管道埋深2.5 m，管道内压力2 MPa，并分别选择管道外径0.6，0.8，1.0，1.2 和1.4 m，管道壁厚度0.011，0.013，0.015，0.017和0.019 m进行对比分析。模型中材料属性如表2所示。

实际管道水毁位置两侧土壤长度可以认为是无限的。为了简化有限元模型，通过比较发现，管道在水毁灾害中悬跨情况下水毁位置两端各截取5 m土壤可以满足模拟计算精度要求，其几何模型如图1所示。

表2　材料属性

图1　管道在水毁灾害中悬跨几何模型Fig.1　Geometric model of pipeline spanning in washout

管道在水毁灾害中漂浮情况下，截取5 m土壤后管道在水动力作用下脱离土壤。这显然与实际情况不符，通过比较发现，水毁位置两端各截取10 m土壤可以满足模拟精度要求，其几何模型如图2所示。

图2　管道在水毁灾害中漂浮几何模型Fig.2　Geometric model of pipeline floating in washout

设置管道与土壤非线性接触，管土之间不可相互侵入，管道与土壤不分离但允许相对滑移。土壤非水毁面与管道两端完全约束，管道外表面所有节点施加均布载荷。以管道在水毁中漂浮为例，选择Solid 186单元，映射单元数为64 336，管道网格尺寸100 mm × 100 mm。鉴于有限元模型较大，网格密集，展示1/4有限元模型，如图3所示。

图3　有限元模型Fig.3　Finite element model

1.3　屈曲特征值

屈曲特征值用于评估特定载荷下结构的稳定性。当载荷值达到临界载荷P时，结构发生屈曲。屈曲前的平衡形式被破坏，新的平衡形式与屈曲前平衡形式有本质区别，结构的内力和变形都因发生了性质上的突然变化。管道在水毁灾害中长距离漂浮情况下，除管道轴向应力达到材料屈服极限发生断裂以外，管道形变达到一定程度而丧失承压能力也会造成灾难性破坏，其中临界载荷P可表示为：

P=λPc

(10)

([Km]+λ[Kn]){δ}=0

(11)

式中：λ为屈曲特征值；[Km]为弹性刚度矩阵；[Kn]为几何刚度矩阵；{δ}为特征位移向量。

2　结果与分析

2.1　位移分析

计算得到管道在水毁灾害中悬跨和漂浮位移如图4所示。

图4　管道在水毁灾害中位移Fig.4　Pipe displacement in washout

从图4可以看出，与土壤接触处管道位移较小，在水毁位置管道位移沿管道铺设方向先增大再减少，位移最大值发生在水毁中心位置。计算得到不同外径管道在水毁灾害中悬跨和漂浮位移，如图5、图6所示。

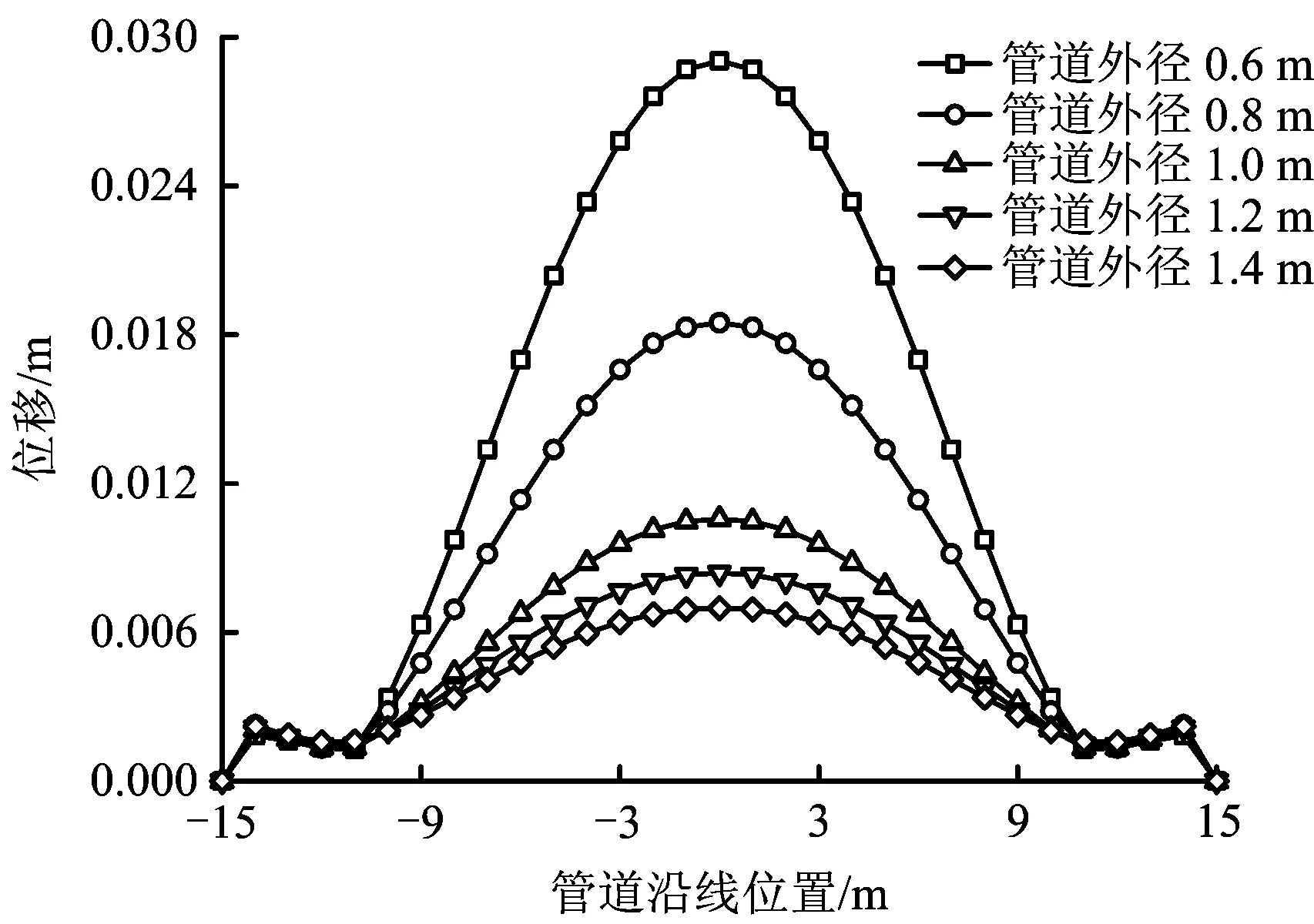
图5　不同外径管道在水毁灾害中悬跨位移Fig.5　Pipeline displacement spanning in washout of different diameter

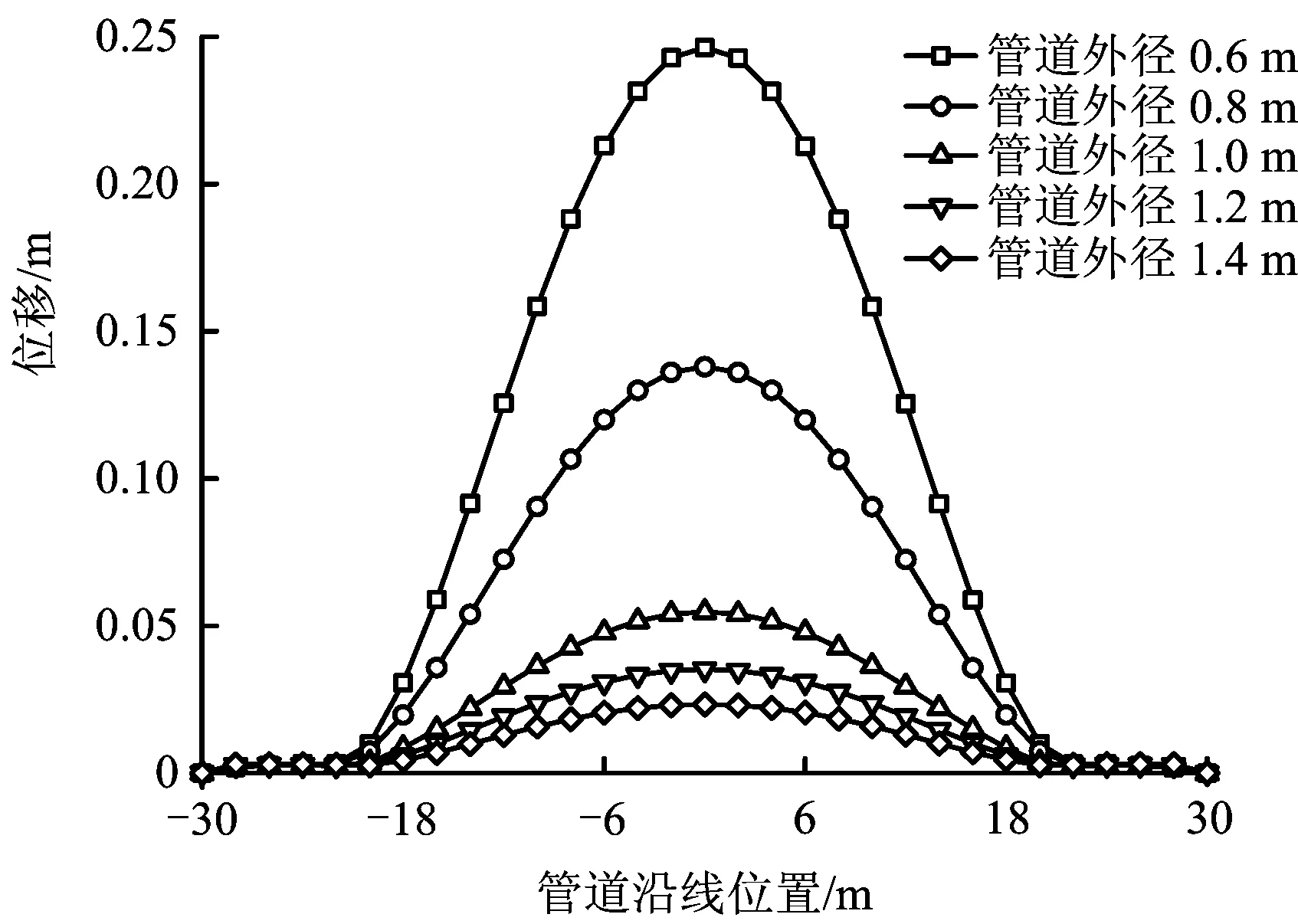
图6　不同外径管道在水毁灾害中漂浮位移Fig.6　Pipeline displacement floating in washout of different diameter

从图5、图6可以看出，随着管道外径的增加，管道最大位移呈降低趋势。这种趋势在管道外径小于1.0 m时表现显著，以管道漂浮为例，管道外径从0.6 m增加至0.8 m、从0.8 m增加至1.0 m，最大位移分别降低约10.8%，8.3%；管道外径从1.0 m增加至1.2 m、从1.2 m增加至1.4 m，最大位移分别降低约2.0%，1.2%。计算得到不同壁厚管道在水毁灾害中悬跨和漂浮位移如图7和图8所示。

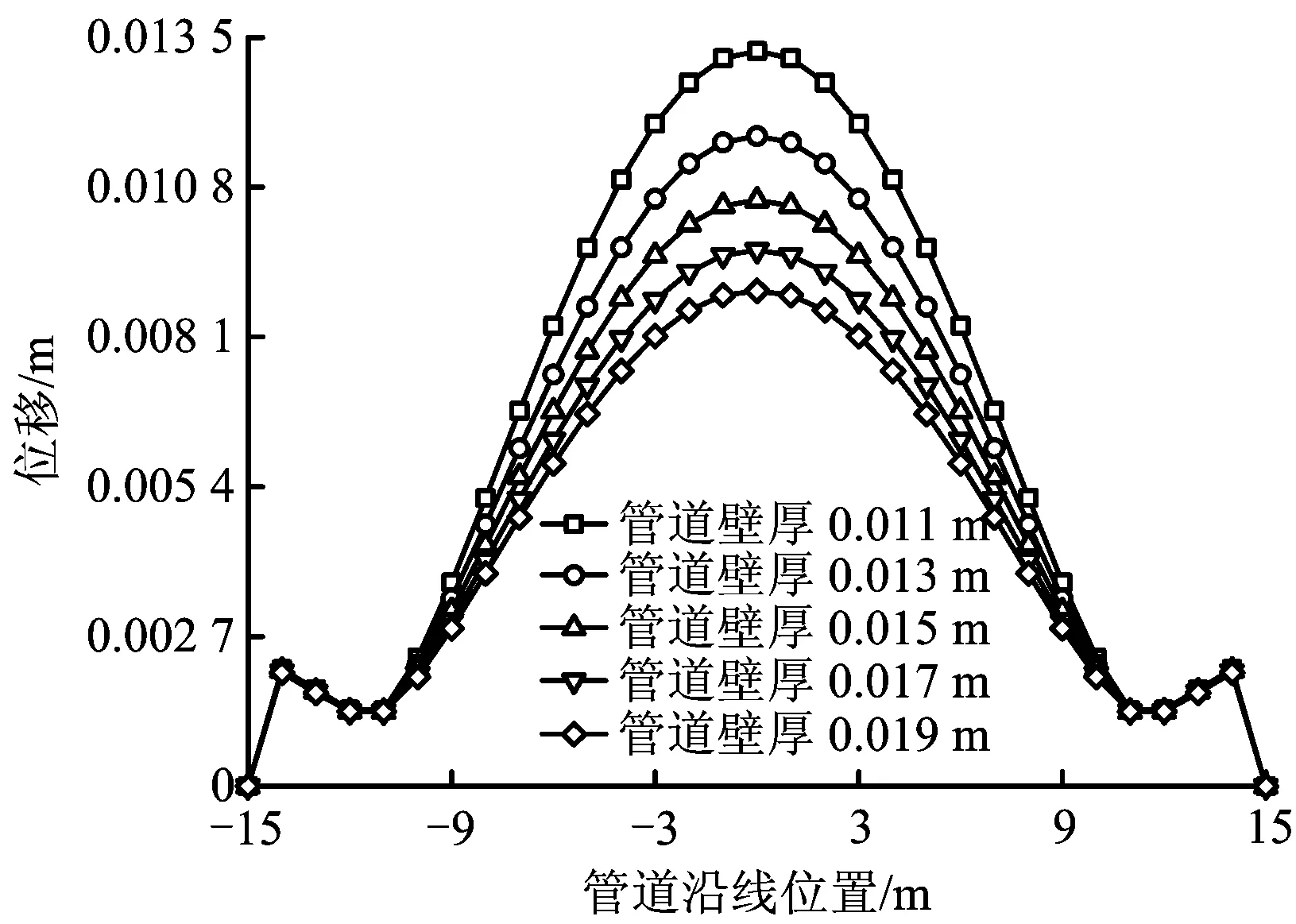
图7　不同壁厚管道在水毁灾害中悬跨位移Fig.7　Pipeline displacement spanning in washout of different thickness

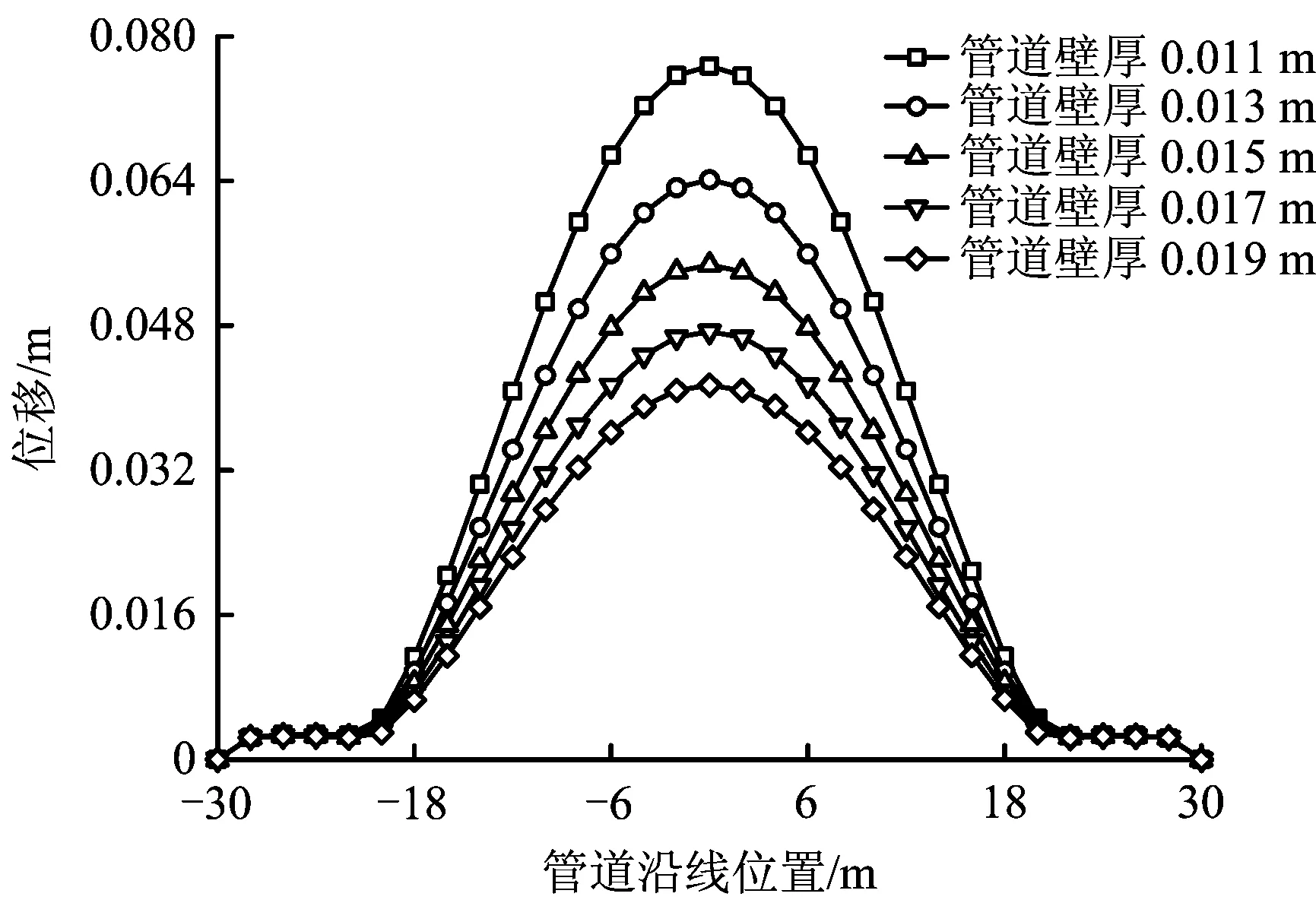
图8　不同壁厚管道在水毁灾害中漂浮位移Fig.8　Pipeline displacement floating in washout of different thickness

从图7和图8可以看出，随着管道壁厚的增加，管道最大位移呈线性降低趋势，壁厚每增加2 mm，最大位移降低约1%。

2.2　屈曲特征值分析

为了确定管道在悬跨和漂浮条件下的极限水毁长度，分别计算得到不同水毁距离下，管道悬跨和漂浮的最小屈曲特征值如图9所示。

图9　不同水毁长度管道最小屈曲特征值Fig.9　Minimum pipeline buckling eigenvalue of different wathout length

从图9可以看出，随着水毁长度的增加，最小屈曲特征值近似呈线性降低。因为当屈曲特征值小于1时结构发生失稳，所以在不考虑安全因子的情况下，管道在水毁中悬跨极限长度约为160 m，管道在水毁中漂浮的极限长度约为200 m。以上2种情况下管道的最小屈曲模态如图10所示。

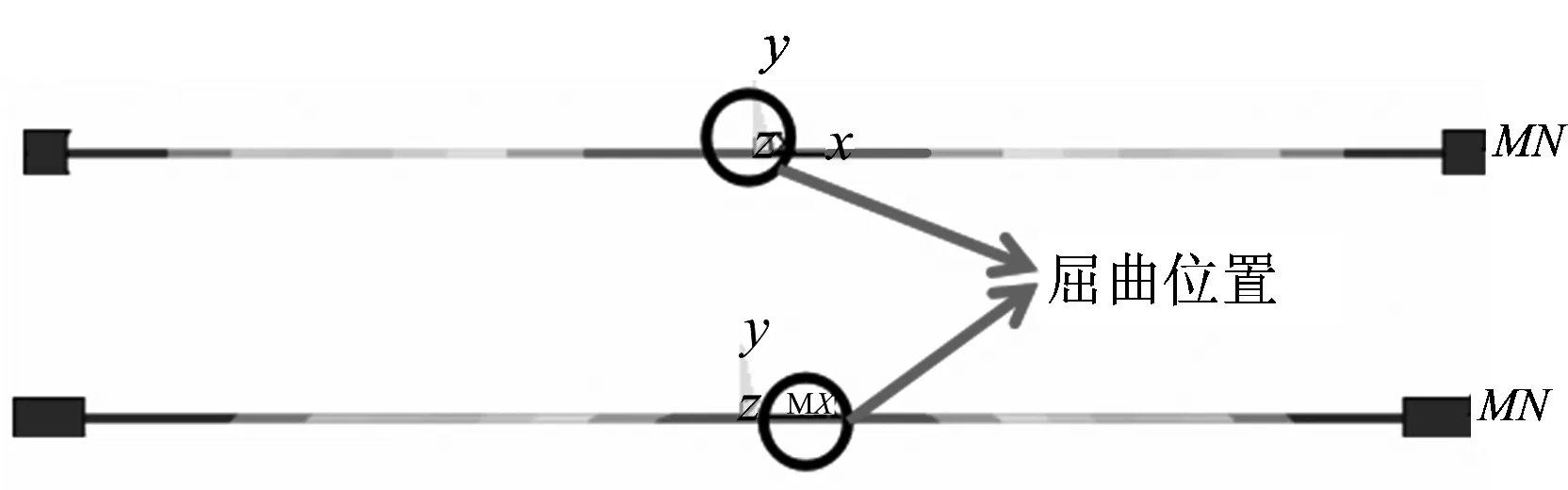
图10　管道在水毁中屈曲模态Fig.10　Buckling mode of pipeline in washout

从图10可以看出，管道在水毁灾害中悬跨最小屈曲模态发生在水毁中心位置，漂浮情况下发生在水毁中心附近偏向流动方向。计算得到不同外径管道在水毁灾害中悬跨和漂浮最小屈曲特征值如图11所示。

图11　不同外径管道最小屈曲特征值Fig.11　Minimum pipe buckling eigenvalue of different diameter

从图11可以看出，随着管道外径的增加，最小屈曲特征值呈显著的线性增长趋势，以管道在水毁中漂浮为例，管道外径从0.8 m增加至1.0 m，最小屈曲特征值增加约160.28%。计算得到不同管道壁厚在水毁灾害中悬跨和漂浮最小屈曲特征值如图12所示。

图12　不同壁厚管道最小屈曲特征值Fig.12　Minimum pipeline eigenbuckling value of different thickness

从图12可以看出，随着管道壁厚的增加，最小屈曲特征值近似呈缓慢的线性增长，以管道在水毁中悬跨为例，管道壁厚从0.015 m增加至0.017 m，最小屈曲特征值增长约5.81%。

3　结论

1)管道在水毁灾害中最大位移发生在中心位置，增加管道外径可以有效抑制管道在水毁灾害中的位移。

2)得到埋地管道在水毁灾害中悬跨和漂浮情况下的极限长度，并确定在该长度下管道的最小屈曲位置。

3)随着管道壁厚的增加，管道在水毁灾害中的稳定性近似呈缓慢的线性增长；增加管道外径显著提高了管道抗屈曲能力。

[1]马延霞, 吴锦强, 唐愚, 等. 成品油管道的极限悬跨长度研究[J]. 西南石油大学学报(自然科学版), 2012,34(4): 165-173.

MA Yanxia, WU Jinqiang, TANG Yu, et al. Maximum suspended length of producton pipeline[J]. Journal of Southwest Petroleum University(Science & Technology Editon). 2012, 34(4): 165-173.

[2]中国石油天然气集团公司. 输气管道环境及地质灾害风险评估方法：Q/SY 1265—2010[S]. 北京：石油工业出版社，2010：7.

[3]张力佳, 王鸿, 郭军, 等. 兰成管道石亭江穿越管段水毁事故原因[J]. 油气储运, 2015, 34(12): 1351-1354.

ZHANG Lijia, WANG Hong，GUO Jun, et al. Causes for flood damage in Shitingjiang River crossing section of Lanzhou-Chengdou Pipeline[J]. Oil & Gas Storage and Transportation, 2015, 34(12): 1351-1354.

[4]李亮亮, 邓清禄, 余伟, 等. 长输油气管道河沟段水毁危害特征与防护结构[J]. 油气储运, 2012, 31(12): 945-949.

LI Liangliang, DENG Qinglu, YU Wei, et al. Damage characteristics and protection structure of washout in long distance transport oil and gas pipeline[J]. Oil & Gas Storage and Transportation, 2012, 31(12): 945-949.

[5]李海川, 吴宏. 靖边-延水关管段汛期水毁现象的防治措施[J]. 油气储运, 2005, 24(8): 53-54.

LI Haichuan, WU Hong. Prevention measures of washout in jingbian-yanshuiguan pipeline section[J]. Oil & Gas Storage and Transportation, 2005, 24(8): 53-54.

[6]Song B, Cheng J J R, Chan D H, et al. Numerical simulation of stress relief of buried pipeline at Pembina river crossing [C]. Proceedings of the ASME International Pipeline Conference 2006, New York, United States, 2007.

[7]张乐天，刘扬，魏立新，等．洪水冲击管道的模拟分析[J]．管道技术与设备，2006(2)：11-12, 17．

ZHANG Letian, LIU Yang, WEI Lixin,et al. Simulation and analysis of impacted pipe[J]. Pipeling Technique and Equipment, 2006(2): 11-12,17.

[8]FURNES G K, BERNTSEN J. On the response of a free span pipeline subjected to ocean currents[J]. Ocean Engineering, 2003, 30(12): 1553-1577.

[9]王晓霖, 帅健. 洪水中漂浮管道的应力分析[J]. 工程力学, 2011,28(2): 212-216.

WANG Xiaolin, SHUAI Jian. Stress analysis of pipeline floating in flood[J]. Engineering Mechanics, 2011,28(2): 212-216.

[10]LI Sijia, DUAN Qingquan, ZHANG Hong, et al. Failure analysis of the floating pipeline with defect under flooding load[J]. Engineering Failure Analysis, 2017, 77: 65-75.

[11]康习锋，张宏，罗茜，等．初始几何缺陷对埋地管道屈曲临界载荷影响研究[J]．中国安全生产科学技术，2015，11(10)：23-27．

KANG Xifeng, ZHANG Hong, LUO Xi, et al. Influence of initial geometric imperfection on critical load of buckling in buried pipeline[J]. Journal of Safety Science and Technology. 2015, 11(10): 23-27.

[12]谭东杰, 施宁, 李亮亮, 等. 洪水冲击流动管道基于DQM的临界长度研究[J]. 西南石油大学学报(自然科学版), 2013,35(4): 173-179.

TAN Dongjie, SHI Ning, LI Liangliang, et al. Research on critical length of flood impacting pipeline within internal flow based on different quadrature method[J]. Journal of Southwest Petroleum University(Science & Technology Editon). 2012, 34(4): 173-179.

[13]Boccotti P, Arena F, Fiamma V, et al. Two small-scale field experiments on the effectiveness of Morison’s equation[J]. Ocean Engineering, 2013, 57(1): 141-149.

[14]帅健, 于桂杰. 管道及储罐强度设计[M]. 北京: 石油工业出版社, 2015.

[15]TIAN Yong, LIU Hao, JIANG Xue, et al. Analysis of stress and deformation of a positive buried pipe using the improved spangler model[J]. Soils and Foundations, 2015, 55(3): 485-492.