CO2/水孔流作用下砂岩真三轴应变分形特征研究*

骆兴科 ，章　光,2，刘明泽,2 ，李小春，胡少斌，张　强

(1. 武汉理工大学 资源与环境工程学院, 湖北 武汉 430070；2. 安全预警与应急联动技术湖北省协同创新中心， 湖北 武汉 430070；3. 中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室，湖北 武汉 430071；4. 河海大学　土木与交通学院，江苏 南京 210098)

数字出版日期： 2017-09-14

0　引言

分形理论用于描述自然界中普遍存在的不规则现象，其主要概念是分形维数，可以作为描述许多物理现象的有力工具[1]。岩石作为一种各向异性的非均质材料，在受力状态下其力学行为具有不确定性与不规则性[2]。因此，用分形理论来研究岩石本质的力学行为与破坏机理具有实际意义。

目前，国内学者结合分形理论与岩石破坏，取得了很多的研究成果。谢和平等研究了岩石节理分形性质[3-5]以及岩石断裂、损伤演化的分形特征[6-7]，研究表明：分维能定量地刻画节理的粗糙性，岩石节理在剪切过程中由于表面损伤而引起的表面分维和截距的演化具有规律性；在岩石的断裂与损伤演化过程中，分形维数能够作为反映岩石损伤断裂机理的特征参数；倪玉山、易顺民[8-9]等通过真三轴压缩试验分别探究了花岗岩断裂表面与三峡坝基岩石脆性断裂的分形特征；高峰、尹贤刚、吴贤振[10-11]等通过岩石单轴压缩力学试验，研究了岩石声发射的分形特征，得出了分形维值随实验时间的变化规律，并以此来分析岩石破坏全过程的损伤演化情况。综上所述，国内学者在对岩石分形的研究上取得了很多有意义的成果，且主要集中在断裂分形与声发射分形。然而，岩石在荷载作用下内部的损伤演化是一个连续的过程，断裂分形的不连续与声发射信号采集误差，均不能准确地描述这一连续过程。在整个试验过程中，应力应变数据的采集是一个连续的过程且具有比较高的精度，岩石内部裂纹扩展、贯通直至破裂都会反映在应力应变曲线上，故而应力应变可作为一种新的表征岩石破坏过程分形维数计算对象[12]。

在此基础上，本文以砂岩为主要研究对象，以CO2、水为孔隙流体介质，通过真三轴试验得到不同流体作用下应力应变数据，分析并比较了砂岩应变分形曲线特征，期以揭示砂岩破坏过程各个阶段的应变分形特征规律。

1　砂岩真三轴压缩试验

1.1　试验样品与装置

本试验岩石样品为均质性较好的四川自贡石英砂岩，根据XRD测试结果，其成分由50.73%石英、34.01%钠长石、10.59%方解石、3.32%伊利石和1.36%蒙脱石组成，见表1。按国际岩石力学学会标准，砂岩被打磨成50 mm×50 mm×100 mm长方体标准试样，将标准试样置于干燥箱内存放以备试验用。

表1　试样矿物组成

试验装置为中国科学院武汉岩土力学研究所自行研制的硬岩高压伺服真三轴试验系统，由轴一加载装置、轴二加载装置、围压加载装置、油源、底座、采集与控制装置以及渗流测试这7部分组成。该系统能够独立精确控制三向轴应力、孔隙流体压力，适用于真三轴应力路径下硬岩的应力应变全过程加卸载试验。孔隙流体压力的精确测量和控制采用ISCO 100DX计量泵。试样3个方向的变形均通过LVDT位移传感器来测量。硬岩高压伺服真三轴试验系统如图1所示。

图1　岩石真三轴试验系统Fig.1　True triaxial testing system of rocks

1.2　试验方案

表2　气体和水对岩石力学特性影响试验参数

图2为砂岩试样压力室安装。试验过程采用偏应力加载控制，加载速率为0.25 kN/s，在注入流体之前将岩样抽真空，注入流体后等到流体在砂岩内部达到平衡之后再进行加载。加载过程中，为了消除加载装置与试样之间的安装间隙，在1方向上首先预加5 kN的偏应力，然后直接加压至岩样破坏。由于干燥砂岩发生的是脆性破坏，为了更好地说明干燥砂岩弹性阶段应变分形特征，在1方向偏应力达到187.5 kN(75 MPa)时稳定一段时间，然后再继续加载。由此采集砂岩破坏全过程的应力应变数据。

图2　砂岩试样压力室安装Fig.2　Sandstone installation

2　试验结果

通过真三轴压缩试验，得到了不同孔隙流体作用下砂岩的物理力学特性，具体参数见表3。从试验结果可知，高压孔隙流体降低了干燥砂岩的峰值强度和弹性模量，相比CO2而言，水对砂岩强度和弹性模量的影响更大。

表3　真三轴压缩试验及计算结果

在Origin中将采集的应力应变数据进行拟合，得到了砂岩的应力-应变曲线和应变-时间曲线。图3为3个岩样的应力-应变曲线，图4为3个岩样的应变-时间曲线。由应力-应变曲线可以看出，干燥砂岩表现出明显的脆性破坏，含水砂岩出现了明显的塑性变形与软化特征，而含CO2砂岩也有一定的塑性变形，其应力在峰后出现回落。

图3　砂岩应力-应变曲线Fig.3　Stress-strain curve of sandstone

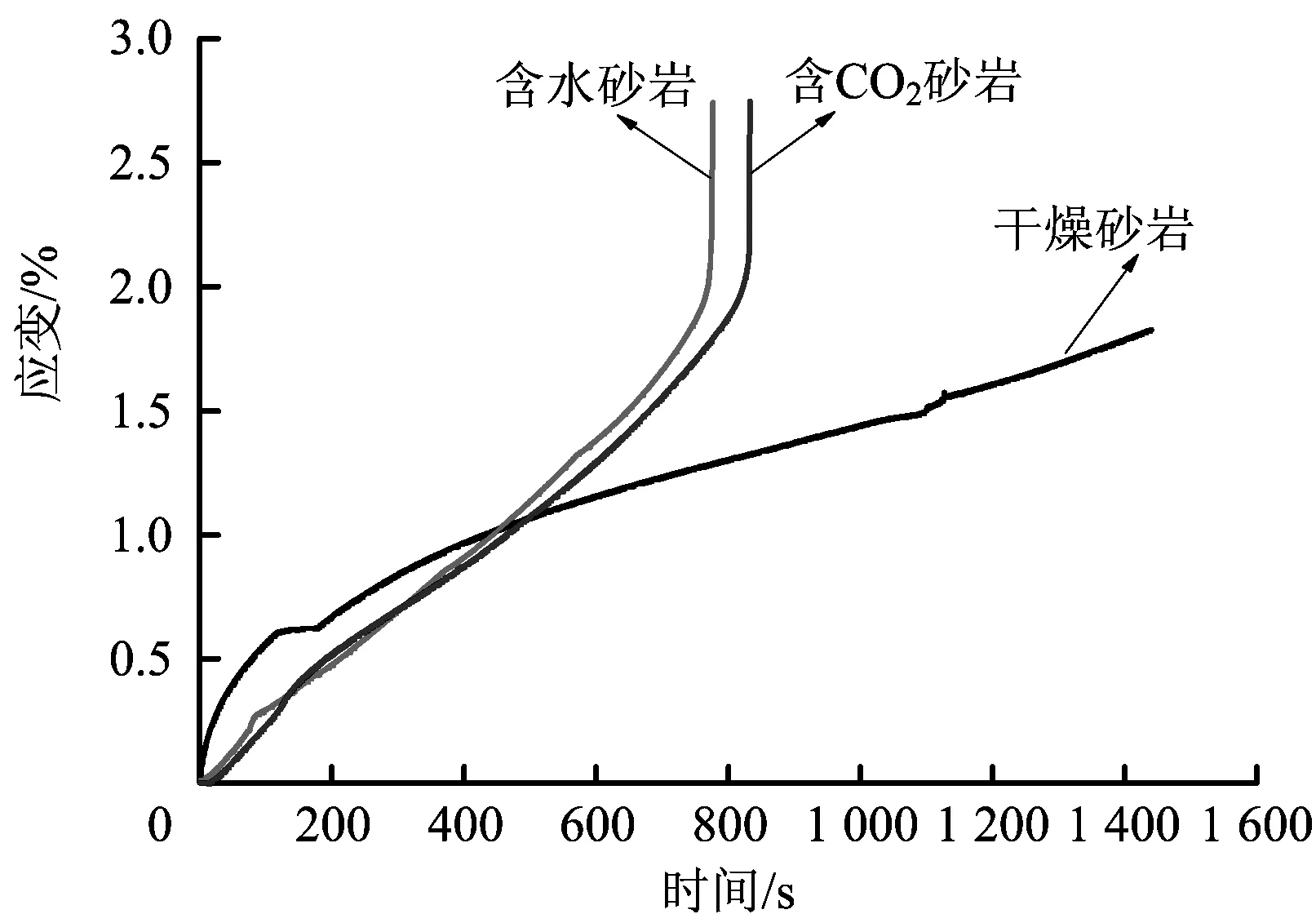
图4　砂岩应变-时间曲线Fig.4　Strain-time curve of sandstone

3　试验结果分析

采用的计算分形维数的方法是计盒维数法，这是一种最常用的计算分形维数的方法。除了自仿射分形以外，计盒维数法可以用来计算不连通的点集、曲线、曲面或立体等分形集，简单实用，适用范围广[13]。

计盒维数的原理是用边长为r的盒子去覆盖分形集，结果有些盒子是空的，有些盒子覆盖了分形集的一部分，得到非空的盒子数N(r)，然后缩小盒子的尺寸，继续覆盖分形集。当r→0时，得到分形维数，其计算公式为：

在本次试验中，计盒维数的计算采用MATLAB编程实现。首先在应变-时间曲线上找到包括特征时间点在内的反映曲线的一系列时间点，在每一个时间点附近取128个应变值作为分形点集。用不同大小的格子去覆盖点集，得到一系列r和N(r)，在双对数坐标中用最小二乘法拟合直线，所得的直线斜率即为所求分形维数[14]。

表4为干燥砂岩的应变分形维数计算结果，为了进一步分析应变分形特征，图5将应变-时间曲线和分形维数-时间曲线绘制在一起。

由计算结果可知，干燥砂岩分形维数范围为1～1.330 3。分析图像可以看出，刚开始加载时，应变分形值迅速上升。这是因为岩石是非均质材料，裂隙分布具有不确定性，当受力裂隙空间被压密时，应变变化的不确定性增加，分形值增大。当弹性阶段稳压时，应力发生突变，随之分形维数也发生突变，迅速下降到1左右，说明这个阶段的砂岩处于一个相对稳定的状态，满足弹性材料的特征。继续加载的一段时间，分形值略有上升，但是上升较慢。进入屈服阶段后，砂岩内部裂纹扩展、贯通，分形值波动起伏较大，最高达到1.330 3，表明了砂岩裂隙扩展的不稳定状态导致应变值波动变化的

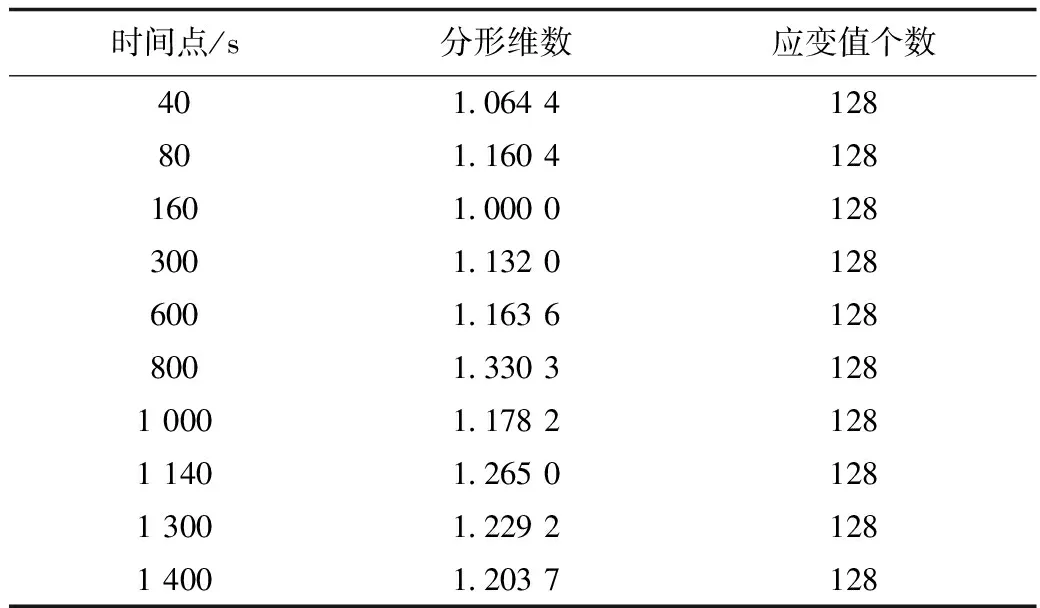
表4　干燥砂岩分形维数计算结果

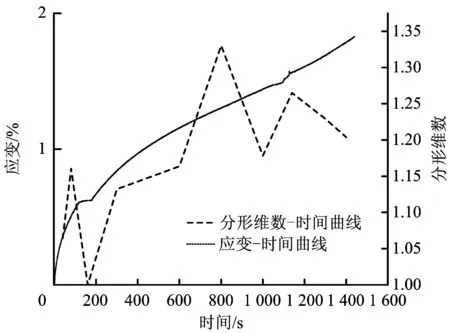
图5　干燥砂岩分形维数-应变-时间关系Fig.5　Fractal dimension-strain-time curve of dry sandstone

无规律性。应变-时间曲线的第2次突变代表的是砂岩破裂阶段，分形值此时也发生突变，之后分形值下降。

表5和图6分别为含水砂岩的分形维数计算结果和分形维数-应变-时间关系图。

表5　含水砂岩分形维数计算结果

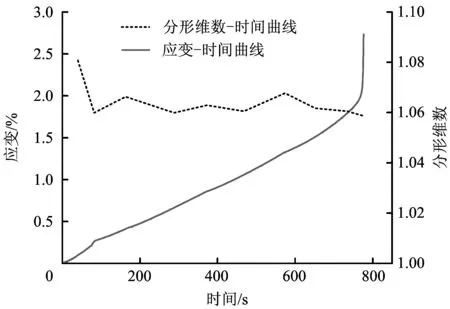
图6　含水砂岩分形维数-应变-时间关系Fig.6　Fractal dimension-strain-time curve of water-bearing sandstone

与干燥砂岩不同，含水砂岩的应变分形值整体较小，最高为1.080 7，最低为1.058 7，并且开始阶段的分形值下降，与干燥砂岩开始阶段分形值上升的规律正好相反。由于砂岩孔隙被高压水充满，加载初期的压密过程实际上是孔隙水排出的过程， 水不具有压缩性，粘性大，含水砂岩应变的变化并不如干燥砂岩那么强烈，这是两者出现差异的根本原因。应变-时间曲线第1次突变点是砂岩骨架开始受力的时刻，此时分形值也发生突变。由于水使砂岩的塑性大大增强，加载过程中分形值只在很小的范围内波动，这是分形曲线最主要的特点。达到峰值应力时，分形-时间曲线与应变-时间曲线同时发生突变，之后分形值下降。

表6和图7分别为含CO2砂岩的分形维数计算结果和分形维数-应变-时间关系图。

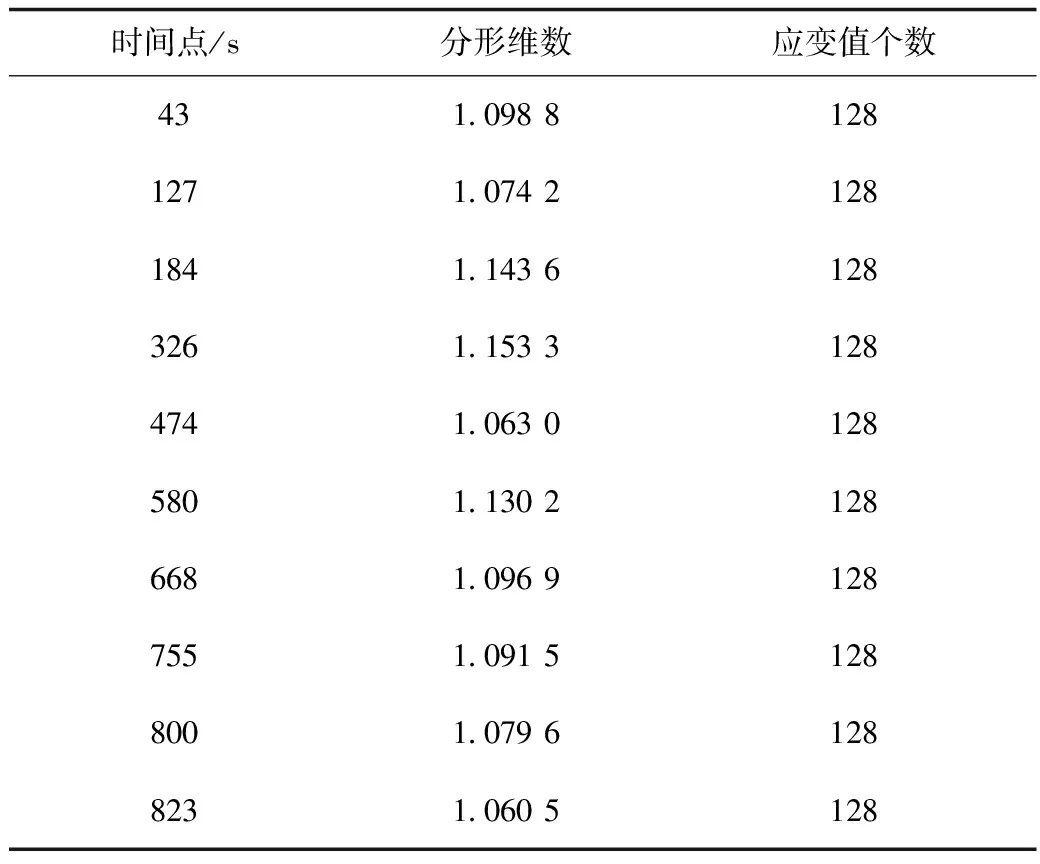
表6　含CO2砂岩分形维数计算结果

图7　含CO2砂岩分形维数-应变-时间关系Fig.7　Fractal dimension-strain-time curve of carbonated sandstone

从整体上来看，含CO2砂岩分形维数范围为1.060 5～1.153 3，介于干燥砂岩与含水砂岩之间。在初期的压密阶段，含CO2砂岩分形曲线与含水砂岩有相似的演化规律，即在达到第1个突变点前，随加载的进行分形是逐渐减小的。在应变发生突变时，分形值也发生突变。从砂岩骨架开始受力到发生破裂的过程中，与含水砂岩分形值不明显的波动相比较，含CO2砂岩波动更大，说明CO2流体与砂岩之间的作用是更加复杂的。事实上，CO2流体不仅可以被黏土矿物吸附(如蒙脱石)[15]，还可以与某些矿物质发生化学反应，因此，CO2的存在对砂岩力学性质的影响很大，其内部裂纹演化过程也是更加复杂的，这与分形值的波动变化现象相吻合。达到峰值应力时，应变与分形均发生突变，之后分形值下降。

对比分析3个分形维数-应变-时间关系图，可以发现，分形维数的范围与最大值排序为：干燥>CO2>水。在砂岩孔隙压密阶段，干燥砂岩与含流体的砂岩应变分形变化规律相反，即干燥砂岩分形维数增大，而含流体砂岩分形维数减小。砂岩从骨架受力到发生破裂的过程中，含水砂岩的分形维数在很小的范围内波动，含CO2砂岩波动较大；而干燥砂岩在弹性阶段分形维数略有上升，屈服阶段分形维数波动较大。在峰后阶段，三者的分形维数均出现下降的趋势，笔者认为这是由于大破坏面出现，砂岩应变变化的不确定性降低。综上所述，含流体砂岩与干燥砂岩的应变分形差异性较大，而CO2、水之间的应变分形存在一定的共性与差异性，这种差异性是由2种流体对砂岩物理力学性质影响的差异所致。

4　结论

1)分形维数的突变与应变的突变具有一致性，分形维数的范围与最大值的排序为：干燥>CO2>水。干燥砂岩的应变分形变化规律为：在孔隙压密阶段，分形维数增大；弹性阶段，分形维数略有上升；屈服阶段，分形维数波动较大；峰后阶段，分形维数减小。

2)含水砂岩和含CO2砂岩的应变分形规律具有共性和差异性。共性表现在孔隙压密阶段和峰后阶段：孔隙压密阶段两者分形维数减小，与干燥砂岩变化规律相反；峰后阶段两者分形维数增大，和干燥砂岩具有一致性。差异性体现在中间阶段：含水砂岩的分形维数在很小的范围内波动，而含CO2砂岩波动较大，这种差异性是由于CO2与砂岩矿物更加复杂的物理化学作用所致。

3)对于砂岩的裂隙扩展阶段，应变分形表现出无规律性，虽然可以说明砂岩此阶段损伤演化的复杂性，但分形维数与裂纹演化状态的具体对应关系还需要更加深入的理论支撑与试验研究。

[1]谢和平.分形几何及其在岩土力学中的应用[J].岩土工程学报,1992,14(1):14-24.

XIE Heping. Fractal geometry and its application in geotechnical mechanics[J]. Chinese Journal of Geotechnical Engineering, 1992,14(1):14-24.

[2]谢和平.分形力学研究进展[J].力学与实践,1996,18(2):10-18.

XIE Heping. Research progress of fractal mechanics[J]. Mechanics in Engineering, 1996,18(2):10-18.

[3]谢和平,王金安.岩石节理(断裂)表面的多重分形性质[J].力学学报,1998,30(3):58-64.

XIE Heping, WANG Jinan. Multifractal behaviors of fracture surfaces in rocks[J].Chinese Journal of Theoretical and Applied Mechanics, 1998,30(3):58-64.

[4]谢和平,周宏伟.基于分形理论的岩石节理力学行为研究[J].中国科学基金,1998,12(4):17-22.

XIE Heping, ZHOU Hongwei. Research on mechanical behaviors of rock joints based on fractal theory[J]. Bulletin of National Natural Science Foundation of China, 1998,12(4):17-22.

[5]王金安,谢和平.剪切过程中岩石节理粗糙度分形演化及力学特征[J].岩土工程学报，1997,19(4):2-9.

WANG Jinan, XIE Heping. The fractal evolution and mechanical characteristics of rock joint roughness in shear process[J]. Chinese Journal of Geotechnical Engineering,1997,19(4):2-9.

[6]谢和平,高峰.岩石类材料损伤演化的分形特征[J].岩石力学与工程学报,1991,10(1):74-82.

XIE Heping, GAO Feng. The fractal features of the damage evolution of rock materials[J]. Chinese Journal of Rock Mechanics and Engineering, 1991,10(1):74-82.

[7]徐志斌,谢和平.断裂尺度的分形分布与其损伤演化的关系[J].地质力学学报,2004,10(3): 268-275.

XU Zhibin, XIE Heping. Relation between fracture-scale fractal distribution and its damage evolution[J]. Journal of Geomechanics, 2004,10(3):268-275.

[8]倪玉山,匡震邦,杨英群.常规真三轴压缩下花岗岩断裂表面的分形研究[J].岩石力学与工程学报,1992,11(3):295-303.

NI Yushan, KUANG Zhenbang, YANG Yingqun. Fractal study of the fracture surface of grantite caused by triaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering,1992, 11(3):295-303.

[9]易顺民,唐辉明.三轴压缩条件下三峡坝基岩石破裂的分形特征[J].岩土力学,1999,18(5):24-28.

YI Shunmin, TANG Huiming. The fractal characteristics of fracture of dam foundation rock under triaxial compression in the three gorges project[J].Rock and Soil Mechanics, 1999,18(5):24-28.

[10]高峰,李建军,李肖音,等.岩石声发射特征的分形分析[J].武汉理工大学学报,2005,27(7):67-69.

GAO Feng, LI Jianjun, LI Xiaoyin, et al. Fractal analysis of the characteristics of acoustic emission of rock[J]. Journal of Wuhan University of Technology,2005,27(7):67-69.

[11]吴贤振,刘祥鑫,梁正召,等.不同岩石破裂全过程的声发射序列分形特征试验研究[J].岩土力学,2012,33(12):3561-3569.

WU Xianzhen, LIU Xiangxin, LIANG Zhengzhao, et al. Experimental study of fractal dimension of AE serials of different rocks under uniaxial compression[J]. Rock and Soil Mechanics, 2012,33(12):3561-3569.

[12]章光,赵顺利,李墨潇,等.岩石单轴压缩试验的应力应变分形特征研究[J].中国科技论文,2015(9):1038-1042.

ZHANG Guang, ZHAO Shunli, LI Moxiao, et al. Research on the fractal characteristic of the rock’s stress and strain under uniaxial compression[J].China Science Paper, 2015(9):1038-1042.

[13]李伯奎,杨凯,刘远伟.分形理论及分形参数计算方法[J].工具技术,2004,38(12):80-84.

LI Bokui, YANG Kai, LIU Yuanwei. Fractal theory and calculation method of fractal parameter[J]. Tool Engineering, 2004,38(12):80-84.

[14]杨书申,邵龙义.MATLAB环境下图像分形维数的计算[J].中国矿业大学学报,2006,35(4):478-482.

YANG Shushen, SHAO Longyi. Estimation of fractal dimensions of images based on MATLAB[J]. Journal of China University of Mining& Technology,2006, 35(4):478-482.

[15]De Jong S M, Spiers C J, Busch A. Development of swelling strain in smectite clays through exposure to carbon dioxide[J]. International Journal of Greenhouse Gas Control, 2014, 24: 149-161.