基于用户兴趣变化的协同过滤推荐算法

李道国1，何狄江，李连杰

（1.杭州电子科技大学信息工程学院；2.杭州电子科技大学管理学院，浙江杭州310018）

基于用户兴趣变化的协同过滤推荐算法

李道国1，何狄江2，李连杰2

（1.杭州电子科技大学信息工程学院；2.杭州电子科技大学管理学院，浙江杭州310018）

文章将用户兴趣设定为变量，重新定义了相似度以及评分预测的计算方法，在一定程度上提高了经典协同过滤推荐算法的精确度；提出结合用户评分时间以及用户访问次数的时间权重模型来描述用户兴趣的变化，使得相似度以及评分预测的计算结果更加合理。实验结果表明，新算法比传统基于项目的协同过滤算法降低了约8%的平均绝对误差、提高了约15%的准确率以及18%的召回率，在一定程度上改善了推荐系统的推荐效果。该算法仅在M ovieLens数据集上进行实验测试，还需要在其他数据集上进行检验。

协同过滤；用户评分时间；用户访问次数；相似度；评分预测

一、引言

互联网的迅猛发展把人们带入了一个新的信息时代，人们周围的数据量正在以指数级的速度增长，怎样能在庞大的数据中快速、准确地找到所需的信息成为难题[1-2]。在这种背景下，个性化推荐应运而生。协同过滤（Collaborative Filtering，简称CF）是其中应用最广泛的推荐算法，其理论基础是人们的从众心理。虽然CF推荐算法在很多方面表现出了独特的优势所在，但也存在一些局限性，例如用户兴趣不是一成不变的。由于所处的环境、年龄等多种因素的影响，每个人的兴趣喜好在发生着变化。而作为帮助用户过滤信息的推荐系统就需要时刻关注用户兴趣的变化才能为用户提供高质量的推荐服务，才能够在飞速发展的互联网时代立足[3]。但是这些因素很难用科学的计算方法来实现，传统的CF推荐算法假定用户评分时间并不影响相似度的度量，但是实际上，不断变化的用户兴趣却在影响着系统推荐的质量。

针对上述问题，本文提出了一种基于用户兴趣变化的协同过滤推荐算法，该算法将用户兴趣随时间的变化情况考虑在内，并通过改善相似度及预测评分的计算方式，来缓解用户兴趣变化对系统推荐结果的影响，进而达到提高推荐精度的目的。

二、研究背景

用户兴趣的准确获取是推荐系统十分重要的研究内容。在初期协同过滤推荐系统运行中，稀疏性和冷启动问题对系统的影响比较大。随着用户对系统使用时间的推移，其兴趣必然也会发生变化，这便增加了系统准确获得用户兴趣偏好的难度，只有解决该问题才能够将用户真正感兴趣的项目推荐给用户。在协同过滤推荐算法中，用户之间相似度的计算结果直接影响着系统的推荐质量。传统相似度的计算方法主要有三种[4]，但是这三种方法都没有将评分的时间考虑在内，认为评分时间不影响用户或者项目之间相似度的计算。虽然刚开始对系统的影响不大，但是随着用户使用系统时间的不断增加，用户的兴趣可能会发生很大的改变，此时再使用传统的方法会使得计算出的相似度出现不准确的结果。另外，在计算预测评分时[5]，仅仅通过相似度的大小来区分每个评分的重要程度，同样也没有将用户评分时间的重要性加以区分，造成预测评分出现不准确，降低了推荐结果的精度。

因此本文提出了基于艾宾浩斯曲线，通过引入用户评分时间及用户访问次数对用户评分建立新的时间权重模型，进而改进传统协同过滤推荐算法中因用户兴趣变化所导致的推荐系统推荐准确性降低的问题。

三、适应用户兴趣变化的协同过滤推荐算法

（一）艾宾浩斯遗忘曲线

19世纪著名的德国心理学家艾宾浩斯（Hermann Ebbinghaus）提出了艾宾浩斯遗忘曲线[6]，如图1所示。他通过实验发现，人在学习之后便会立即开始遗忘，并且遗忘的速度是不同的，刚开始遗忘的速度最快，急剧下降，之后便开始逐渐的缓慢，直到趋于稳定，随后遗忘停止。

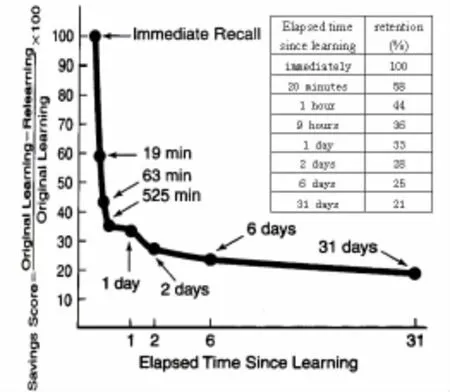
图1 艾宾特斯遗忘曲线

用户兴趣的变化符合艾宾特斯遗忘曲线，因此遵循以该理论为基础的权值计算原则，在传统基于项目的协同过滤推荐算法的基础上引入用户评分时间以及用户访问次数的权值模型来描述用户的兴趣随时间的变化。

（二）基于艾宾特斯遗忘曲线的权重定义

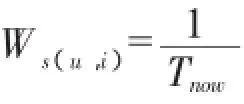
综上所述，新的时间权重模型表示为：

其中n为项目的总数。新的权重模型反映了用户的长期兴趣偏好的同时又准确地反映了用户兴趣的变化。

（三）改进后算法的主要步骤

输入：目标用户u访问过的项目集合Iu。

输出：目标用户u的TOP-N项目推荐列表。

Step1：对目标用户访问过的项目集合Iu中的项目i，根据公式（1）和（2）计算的值。

Step2：根据公式（3）计算项目i（i∈Iu）与其他项目的相似度，根据计算结果确定项目i的最近邻集合Ki，将所有Ki中的数据合并为集合Z，Z=∑Ki。

Step3：统计项目集合Iu和集合Z中重合的项目，并把这些项目从Z中删除，最终得到目标用户u的候选推荐集合Zu，Zu=Z-Iu。

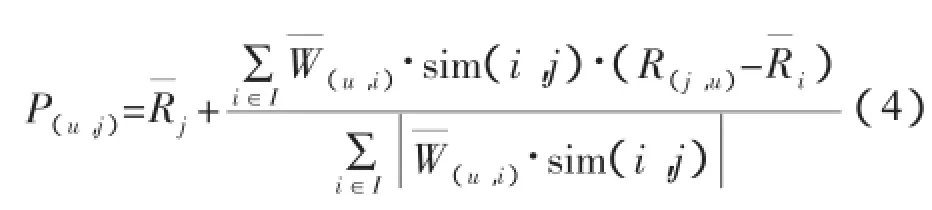
Step5：将Step4中根据计算出的项目预测评分，依据降序从大到小进行排列，选择排在最前面的N个项目推荐给目标用户u。

四、实验结果及分析

（一）实验数据与环境

实验数据采用Minnesota大学GroupLens研究小组创建的MoieLens数据集中的100 K的数据集进行实验。该数据集中记录了总共有943个用户对1 682部电影的1×105条评分。电影的评分分值在[0-5]之间不等，用户对电影的喜爱程度随着评分分值的增加而递增[7]。数据集中的数据按照4∶1的比例划分为训练集和测试集[8]。

实验环境是Intel（R）Core（TM）i3-2310M2.10GHz CPU，内存2GB，Microsoft Windows7操作系统，算法使用Matlab语言编写来实现。

（二）检验指标

1.平均绝对误差（MAE）。MAE是推荐系统中最常用也是最简单的一种性能评价标准，它通过计算出所有的预测评分与实际评分之间的偏差来衡量算法的优劣[3]。MAE值的计算如公式（5）所示：

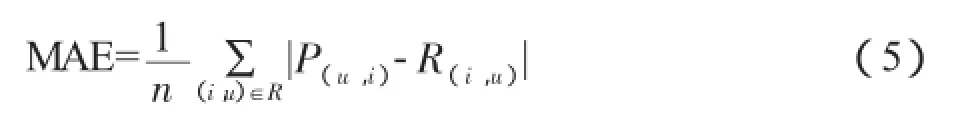
预测评分为P（u，i）（表示用户u对电影i的预测评分），用户实际评分Ru，i（表示用户u对电影i的真实评分），n表示Pu，i或者 Ru，i的数量，MAE值越小说明该算法就越精确。MAE值的计算如公式所示。

2.准确率（precision）。推荐的准确率就是在N个推荐给用户的项目中，同时出现在测试集中的概率。计算如公式（6）所示：

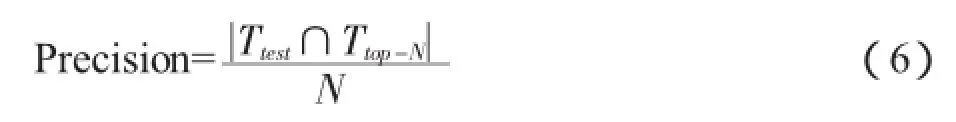
3.召回率（recall）。对于目标用户的推荐召回率则是测试集中目标用户已经选的项目中，出现在该用户的推荐集中的概率，计算如公式（7）所示：

其中 Ttest表示在测试数据集中项目的数量，Ttop-N表示系统推荐给用户的N个项目。准确率越高说明该算法的效果越好，同样，召回率越高说明算法的效果越好。

（三）实验分析

实验一：根据最近邻个数的不同，MAE值的变化情况

最近邻个数分别取10、20、30、40、50（实验二、三取值相同），利用公式（5），计算出本文提出的新算法以及传统基于项目的CF推荐算法MAE值随最近邻个数的不同的变化情况如图2所示：

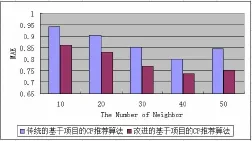
图2 最近邻集合取值对MAE值的影响

从图2看出，引入用户评分时间以及用户访问次数的CF推荐算法在最近邻个数取值范围内，MAE值均小于传统的CF推荐算法。MAE值平均降低8%。

实验二：根据最近邻个数的不同，Precision的变化情况

利用公式（6），计算出本文提出的新的算法与传统基于项目的CF推荐算法Precision值随不同的最近邻个数的变化情况，如图3所示：

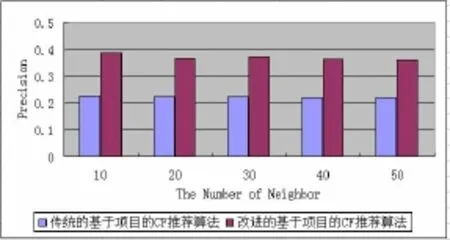
图3 最近邻取值对Precision的影响

从图3可以看出，改进后的算法在最近邻个数取值为[10，50]时，Precision的值均大于传统基于项目的CF算法。Precision平均提高 15%。从图 3还可以看出Precision的值波动不大，其值不与最近邻个数的取值相关。

实验三：根据最近邻个数的不同，Recall的变化情况

利用公式（7）本文提出的新的算法与传统基于项目的CF推荐算法的Recall值随最近邻个数不同的变化情况如图4所示：

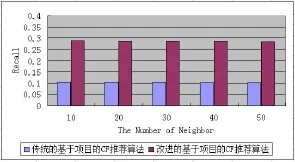
图4 最近邻取值对Recall值的影响

从图4可以看出，在最近邻介于10～50之间时，改进的基于项目的CF推荐算法的Recall值均大于传统基于项目的CF推荐算法。Recall值平均提高18%。从图4还可以看出Recall的值不随最近邻取值的不同而变化，波动不大。

通过以上三组对比实验结果可知，本文提出的算法在MAE、Precision、Recall三项指标上都有很好的表现性能。这是因为改进后的算法在相似度以及评分预测的计算过程中反映了用户兴趣的变化，在一定程度上有助于提高系统的推荐准确度。

五、总结

本文针对传统的基于项目的协同过滤推荐算法中没有将用户兴趣的变化反应在相似度以及预测评分的计算过程中，提出了一种基于用户兴趣变化的协同过滤推荐算法。新的算法通过结合用户评分时间以及用户浏览次数建立新的时间权重模型，改善两个项目相似度以及预测评分的计算。通过实验一、二、三的结果可知，新的算法能够在一定程度上缓解用户兴趣随时间变化的问题，在一定程度上提高了推荐系统的准确性。

[1]罗琦，缪昕杰，魏倩.稀疏数据集协同过滤算法的进一步研究[J].计算机科学，2014（6）：264-268.

[2]邓华平.基于项目聚类和评分的时间加权协同过滤算法[J].计算机应用究，2015（7）：1966-1969.

[3]王鹏.基于矩阵分解的推荐系统算法研究[D].北京交通大学，2015.

[4]李红梅，郝文宁，陈刚.基于改进LSH的协同过滤推荐算法[J].计算机科学，2015，42（10）：256-261.

[5]孙辉，马跃，杨海波，等，2014.一种相似度改进的用户聚类协同过滤推荐算法[J].小型微型计算机系统（9）：1967-1970.

[6]杨峥.基于用户兴趣变化的协同过滤推荐算法研究[D].燕山大学，2015.

[7]刘占兵，肖诗斌，2015.基于用户兴趣模糊聚类的协同过滤算法[J].现代图书情报技术（11）：12-17.

[8]柯良文，王靖，2015.基于用户特征迁移的协同过滤推荐[J].计算机工程（1）：37-43.

（责任编辑：C 校对：L）

F062.5

A

1004-2768（2017）01-0019-03

2016-09-22

李道国（1965-），男，浙江杭州人，杭州电子科技大学信息工程学院教授，研究方向：电子商务、模式识别与人工智能；何狄江（1991-），男，浙江绍兴人，杭州电子科技大学管理学院硕士研究生，研究方向：供应链管理；李连杰（1991-），女，内蒙古赤峰人，杭州电子科技大学管理学院硕士研究生，研究方向：电子商务。何狄江为通讯作者。