压力传感器动态误差修正方法的FPGA实现
杨文杰,张志杰,王代华,陈青青
(中北大学仪器科学与动态测试教育部重点试验室,太原 030051)
压力传感器动态误差修正方法的FPGA实现
杨文杰,张志杰*,王代华,陈青青
(中北大学仪器科学与动态测试教育部重点试验室,太原 030051)
为了实时修正由于压力传感器动态特性引起的动态误差,提出了一种基于IIR数字补偿滤波器的FPGA实现方案。该方案首先依据压力传感器动态标定时的输入和输出数据利用改进的最小二乘算法建立全面描述传感器系统的数学模型,继而运用零极点配置方法重新配置模型零极点得到最优IIR补偿器模型及参数,其次在保证补偿器性能无失真或失真很小的基础上使用MATLAB工具量化补偿器模型参数,最后在以FPGA为控制核心的数据采集及存储系统的基础上应用量化的IIR补偿器模型参数设计了IIR补偿器软核,从而实现传感器动态误差的实时修正。实验结果表明:该方案能够实时有效地修正传感器动态误差。
压力传感器;动态特性;动态误差;IIR滤波器;FPGA;软核
在动态测试中当传感器的工作频带不能有效覆盖被测信号的各种模态及频率分量时,工作频带范围外的信号频率分量就会被“畸形化”,最终导致测量结果无法表征输入信号,产生较大的动态误差[1-7]。而研制动态性能优异的传感器是很困难的[8],许多传感器的动态性能远不能满足各种动态测试的要求,因而研究传感器动态性能改进的方法具有理论和实际意义。在众多改进传感器动态性能的方法中,采用设计动态补偿器的方法最为简单直接可行。对于在线实时修正由于传感器的动态特性不足引起的动态误差需要设计广泛应用于数字信号处理领域的数字补偿滤波器[9]。FPGA(现场可编程门阵列)拥有良好的并行运算能力,以及可配置、可扩展等优点,且基于FPGA设计的数字滤波器成本低廉(无需更改硬件电路),且可靠性高,重复性好,在数字补偿滤波器中得到了广泛的应用。
1 改进最小二乘算法建模原理与实现
单输入、单输出线性定常系统可以用下面差分方程描述[8]
A(d-1)y(k)=B(d-1)u(k)
(1)
如果考虑噪声,则式(1)可写为
A(d-1)[y(k)-ey(k)]=B(d-1)[u(k)-eu(k)]
(2)
式(2)简写为
A(d-1)y(k)-B(d-1)u(k)=ε(k)
(3)
式中:u(k)为系统输入数据,y(k)为输出数据, d-1为延迟算子,ε(k)为拟合残差,有
(4)
(5)
ε(k)=A(d-1)ey(k)-B(d-1)eu(k)
(6)
建模就是根据压力传感器动态标定实验的输入、输出序列{[u(k),y(k)]| k=1,2,…,N}确定模型阶次n,并对模型参数ai,bi,i=0,1,…,n(a0=1)做出估计。
由于建模时输入是假定的理想阶跃信号序列,此时输入端噪声可不予以考虑。如果假定输出端是零均值的白噪声,式(6)可变为
ε(k)=A(d-1)ey(k)=A(d-1)e(k)
(7)
也即
e(k)=ε(k)/A(d-1)
(8)
式中:1/ A(d-1)可称为滤波器。则式(3)可变为A(z-1)[y(k)/A(z-1)]=B(z-1)[u(k)/A(z-1)]+e(k)
(9)
令

(10)

(11)
则式(3)可写为

(12)


步骤2 设迭代第l次时,求得
计算:
序列,对下式作最小二乘估计

(13)

步骤4 令l=l+1,回到步骤2,直到迭代收敛或者达到迭代次数为止。当迭代收敛时,可以得到式(14):

(14)
它将使J=∑e2(k)达到最小。
传感器离散传递函数的一般形式为:

(15)
依据压力传感器动态标定时的输入和输出数据利用上述方法得到的压力传感器数学模型为

(16)
为了较直观的检验所建立模型的好坏,现用相同的输入信号序列u(k)激励模型G(z-1)得到的响应与标定实验时压力传感器对阶跃信号的响应如图1所示。

图1 传感器响应曲线与改进的最小二乘拟合曲线
由图1可知,用改进的最小二乘算法拟合的数据曲线与压力传感器标定实验得到的数据曲线有很高的拟合度,说明建模算法是可行的,是先进的。与此同时,传感器系统阶跃响应存在超调量大,响应时间长等不足,应用时会产生较大的动态误差,因此需要改善传感器的动态性能。
2 零极点补偿方法的原理与实现
传感器的动态特性与其传递函数的零极点尤其是极点位置关系密切[10]。对传感器传递函数的零极点进行分析,观察它们对传感器动态性能的影响,然后串接一个补偿模块,将原来不符合要求的零极点消去,配以新的零极点,使系统动态特性得以改善,这便是零极点补偿方法[11]。对于只有一对共轭极点的二阶系统传感器模型可直接应用下列公式求解满足特定要求的极点(高阶需要研判各极点对动态性能影响程度)。

(17)

(18)
式中:α为新配置极点的实部,β为新配置极点的虚部,T为采样间隔,现取0.5μs,Trr为所要求响应时间,现取6μs,ξe为等效系统的阻尼比,现取0.95。由式(17)与式(18)求出:
pe1,2=0.881 8±i0.036 3
由公式

(19)
(20)
其中Ge(z)为补偿模型,be为系数,p1,p2为传感器二阶模型极点。依据式(19),式(20)设计的补偿滤波器为

(21)
传感器系统串联补偿系统前后阶跃响应曲线如图2所示。

图2 串联补偿系统前后传感器阶跃响应曲线
图1和图2对比表明,在原传感器模型后面串联一补偿环节后传感器的动态性能得到很大程度的改善,也直接表明补偿方法是可取的。上述补偿器的设计方法特别容易在计算机上编程实现,尤其在MATLAB上编程实现,这也是选择上述补偿器设计方法的一个重要原因。
3 补偿器系数量化方法及实现
在IIR滤波器的FPGA实现过程中,由于该滤波器是一个有反馈环节的闭环系统,且中间过程存在除法运算,所以在运算过程中无法做到全精度运算[12],即使实现了全精度运算,运算过程中需要的寄存器字长是难以接受的,因此在进行FPGA实现之前,有必要确定滤波器系数字长。在MATLAB命令窗口输入下列命令
m=max(max(abs(a),abs(b)));
Qm=floor(log2(m/a(1)));
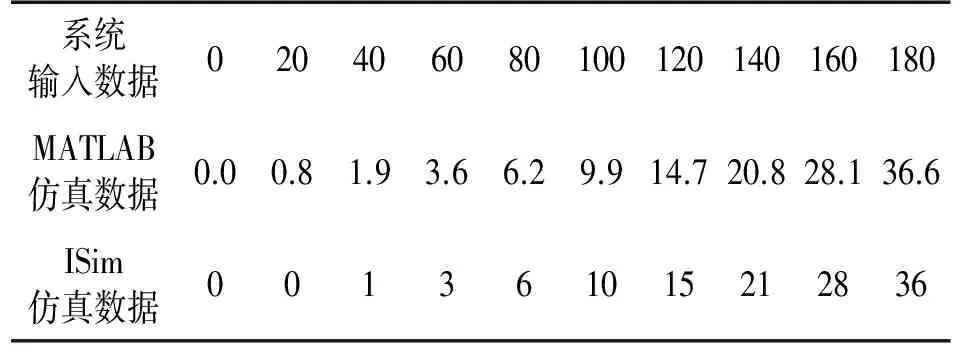
if Qm Qm=Qm+1; end Qm=2^Qm; Qa=round(a/Qm*(2^(n-1)-1)); Qb=round(b/Qm*(2^(n-1)-1)); 其中,a,b,Qa,Qb分别为量化前后滤波器系数,n为带符号位的量化字长。 由于即使是常系数的除法运算在FPGA实现也是十分耗费资源的,但当除数是2的整数幂次方时,可根据二进制的特点直接采用移位的方法近似实现除法运算。而移位运算不仅占用的硬件资源少,且运算速度快。为此上述方法有意将分母系数的第1项设置为2的整数幂次方形式。上述滤波器系数量化字长n可依据不同字长量化后频率特性与滤波器量化前的频率特性对比确定。图3是滤波器系数依据不同字长量化前后频率特性曲线。 图3 IIR滤波器系数量化字长效应 由图3可知,IIR滤波器系数量化字长小于16 bit时滤波器的性能会降低,当量化字长大于16 bit时,精度会随着量化字长增大而提高,但FPGA消耗的内部资源会随着量化字长增大而显著增多,同时处理速度会越来越低。综合精度,资源消耗和处理速度等,现取系数量化字长为16 bit。 依据上述补偿滤波器量化方法,得到所设计滤波器的差分方程为 16 384y(n)=691x(n)-993x(n-1)+688x(n-2)- [-28 134y(n-1)+12 137y(n-2)] (22) 根据式(22),求取式右边运算结构后,除以16 384即完成一次完整的滤波运算。根据FPGA的特点,上式采用向右移14 bit的方法近似实现除以16 384运算,IIR滤波器的实现结构框图如图4所示。 图4 IIR滤波器实现结构框图 从图4可以看出,对于零点系统的实现结构可以看做没有反馈环路的FIR滤波器结构;系统极点的实现结构,即求取Y信号的过程也可以看成一个不带反馈结构的电路结构。整个IIR滤波器的闭环过程只在求取S的减法器和实现除法运算的移位运算过程中完成。上述乘法器可以通过调用通用的乘法器IP核实现。图5是基于上述结构在FPGA上设计的IIR滤波器软核RTL原理图。图6是在Xilinx公司提供的集成软件环境ISE上实现IIR滤波器功能仿真图。 图5 基于FPGA的IIR滤波器软核RTL级原理图 图6 基于FPGA的IIR滤波器功能仿真图 为了验证所设计的IIR滤波器软核功能是否满足设计要求,现将部分图6中输入和输出数据(分别为蓝色和红色部分)以及在同样输入数据条件下利用MATLAB工具得到的仿真输出数据(保留两位有效数字)绘制于表1,作一下对比。 表1 ISim仿真数据和MATLAB仿真数据对比 表1通过ISim仿真数据与MATLAB仿真数据对比表明,随着输入数据的增大,ISim仿真数据与真值之间的相对误差会减小,即基于FPGA的IIR滤波器输出精度会随着输入数据的增大而提高。由于现场测试时以FPGA为核心的采集模块输出数据,也即所设计IIR滤波器软核输入数据,其大小一般都成百上千,因此所设计的IIR滤波器能够以较高的精度修正压力传感器由于动态特性不足产生的动态误差。 图7 传感器第1次动标修正前后输出数据 为了检验压力传感器动态误差修正方法的FPGA实现性能,现将设计的IIR滤波器软核应用在以FPGA为控制核心的压力传感器标定系统中,得到修正前后的部分数据曲线如图7、图8所示。 图8 传感器第2次动标修正前后输出数据 图7、图8表明,处理后压力传感器阶跃响应的超调量得到明显减小,响应时间得到明显缩短。即压力传感器由于动态特性不足产生的动态误差得到了很大程度地修正。 本文在以FPGA为控制核心的数据采集及存储系统的基础上,提出了一种压力传感器动态误差实时修正方法的实现方案。压力传感器动态标定实验表明:该方案可以显著修正由传感器系统特性引起的动态误差。同时该方案具有条理清晰,易于实现,效果明显等优点。综上,该方案可以应用在修正压力传感器动态误差的测试试验中。 [1] 刘清,殷曹国华.模型参考和误差白化的传感器动态补偿算法[J]. 控制理论与应用,2009,26(3):256-260. [2] 吴健,张志杰,王文廉.传感器动态误差高速并行修正方法及其FPGA实现[J]. 传感技术学报,2012,25(1):67-71. [3] 吴建. 传感器动态补偿滤波器及其硬件实现方式研究[D]. 中北大学,2012. [4] 李悦,钟新跃.一种传感器动态误差实时修正方法及其FPGA实现[J]. 核电子学与探测技术,2012,32(9):1112-1115. [5] 黄晓敏. 传感器动态特性补偿方法研究及其FPGA实现[D]. 中北大学,2015. [6] 张海龙,刘一江,马铁华,等. 基于DSP和IIR的传感器动态特性改善单元[J]. 传感技术学报,2013,26(9):1254-1257. [7] 禹东川. 压力传感器动态性能分析与动态补偿[J]. 中国仪器仪表,2003(7):9-11. [8] 黄俊钦. 测试系统动力学[M]. 北京:国防工业出版社,2013. [9] 罗海. 基于FPGA的高速IIR数字滤波器设计与实现[D]. 电子科技大学,2007. [10] 赖富文,张志杰,张建宇,等. 基于动态特性补偿的冲击波测试数据处理方法[J]. 爆炸与冲击,2015,35(6):872-873. [11] 杨文杰,张志杰,赵晨阳,等. 基于零极点配置理论的压力传感器动态特性补偿[J]. 科学技术与工程,2016,16(2):78-82. [12] 杜勇. 数字滤波器的MATLAB与FPGA实现[M]. 北京:电子工业出版社,2014. 杨文杰(1990-),男,河南驻马店人,硕士研究生,主要从事动态测试系统搭建,信号获取,存储与处理以及智能仪器开发,1210921680@qq.com; 张志杰(1965-),男,山西五台人,现任中北大学教授、博导,仪器科学与技术学科带头人之一,主要从事动态测试理论、技术与应用,信号处理理论与技术的研究,zhangzhijie@nuc.edu.cn。 Realization of Dynamic Error Correction Method of Pressure Sensor by FPGA YANGWenjie,ZHANGZhijie*,WANGDaihua,CHENQingqing (Key Laboratory for Instrumentation Science and Dynamic Measurement,Ministry of Education,North University of China,Taiyuan 030051,China) In order to correct the dynamic error caused by the dynamic characteristics of the pressure sensor in real time,a FPGA implementation scheme based on IIR digital compensation filter was proposed. Firstly,on the basis of the input and output data of the dynamic calibration for pressure sensor,a mathematical model describing the sensor system comprehensively was established by using the improved least squares algorithm,and then the optimal IIR compensator model and parameters were obtained by using the pole-zero configuration method to reconfigure the pole-zero of the model. Secondly,in order to guarantee the compensator performance without distortion or low distortion,the compensator model parameters were quantified by using MATLAB. Finally,the IIR compensator soft core was designed by using the quantized parameters of the IIR compensator model in the data acquisition and storage system with the FPGA as the control core so as to realize the real-time correction of transducer’s dynamic error. The experimental results show that the proposed scheme can correct the dynamic errors of sensors in real time. pressure sensor;dynamic characteristic;dynamic error;IIR filter;FPGA;soft core 2016-08-31 修改日期:2016-11-09 TP274 A 1004-1699(2017)03-0402-05 C:7230 10.3969/j.issn.1004-1699.2017.03.012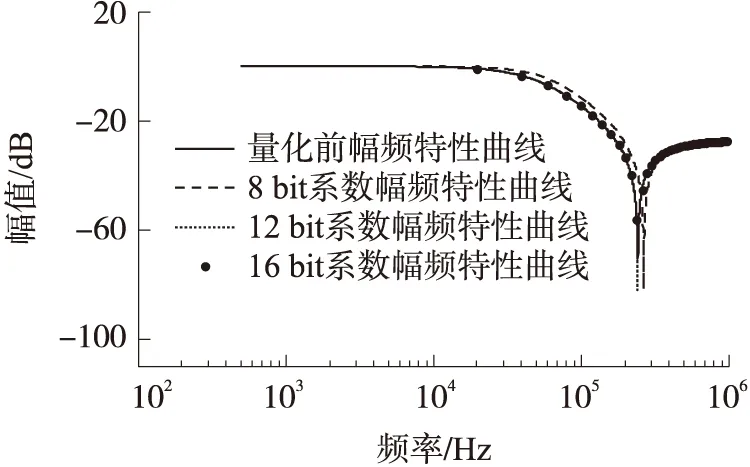
4 基于FPGA的IIR滤波器软核设计




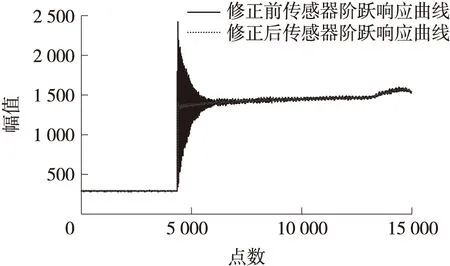
5 结论



