低成本车载组合导航在GPS失效时的算法设计

姜博文,王可东

(北京航空航天大学 宇航学院,北京 100191)



低成本车载组合导航在GPS失效时的算法设计

姜博文,王可东*

(北京航空航天大学 宇航学院,北京 100191)

在低成本MEMS-IMU/GPS车载组合导航应用中,城市中建筑的遮挡会造成GPS失效,此时由于MEMS器件精度较低,导航精度会迅速降低甚至发散。针对此问题,引入车辆的天向和侧向速度约束作为虚拟观测,并且考虑到GPS失效时段由于低精度MEMS-IMU带来的非线性,在不做小角度近似的条件下,推导出非线性速度约束作为虚拟观测,利用非线性UKF滤波算法进行估计,以进一步改善导航性能。车载实验表明,提出的非线性速度约束算法能够有效提高GPS失效时的精度,并且在GPS信号再次有效时能够快速收敛。

GPS;MEMS;UKF;组合导航;惯性导航系统

MEMS-IMU/GPS的组合导航系统由于其低成本和小型化等优点得到了越来越广泛的应用[1-2],但是在城市中GPS容易受高楼、桥梁或隧道等遮挡而失效,给组合系统带来如下问题[3]:一是当GPS失效时组合系统运行在纯惯导解算状态,由于MEMS-IMU的精度较低,解算结果会迅速发散。针对此问题,文献[4]利用里程计的输出作为GPS失效时的观测信息来解决这个问题,这种方案在工程中已有应用,但是新引入额外的传感器无疑增加了实现的成本。文献[5]通过假设车辆侧向和天向速度为零以限制惯导误差的快速发散,这种方案实施简单,但是精度有限,而且只适合于简单的直线运动。文献[6-8]等分别通过神经网络、遗传算法、支持向量机等方法,在GPS信号有效时进行在线训练,当GPS信号失效时利用训练好的模型来估计误差以达到提高精度的效果,但是这些方法由于巨大的计算量在应用中受到了一定限制;第2个问题是在低成本的IMU应用中,当GPS信号再次有效时,在GPS失效期间累积的导航误差已经不是小量,近似的线性模型已经不再适用,线性传递下的系统状态和协方差已不能准确描述系统信息,采用线性的KF(Kalman Filter)进行滤波难以立即对GPS恢复后的状态做出正确的估计。

针对上述问题,本文考虑到城市应用中GPS失效持续时间不长但是比较频繁,并且低精度MEMS-IMU在短时的失效内能造成较强的非线性,因此在传统线性速度约束(用速度误差的线性函数作为观测)的基础上建立了非线性的速度约束(用速度误差的非线性函数作为观测)模型,在GPS失效时将速度约束作为虚拟的观测,并用UKF(Unscented KF)滤波算法在GPS失效时进行估计,提高估计精度,当GPS信号恢复时候能快速收敛,改善导航性能。

1 组合系统模型

1.1 系统误差模型

1.1.1 非线性误差模型

记n为真实地理系,n′为计算系。设n系可以通过三次转动得到n′系,三次转角依次为αz、αx和αy,根据这三次旋转可算出n系到n′系的转换矩阵:

其中cα、sα分别表示cosα、sinα。

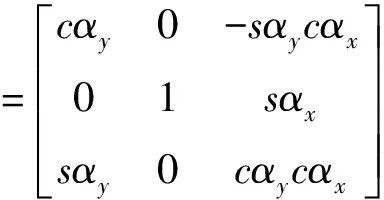
则系统的状态方程[9]可以表示为:

(1)

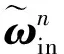
(2)

令15维状态变量x=[αδvδpbabg]T其中α=[αxαyαz],δp=[δLδλδh]T,ba,bg分别为加速度计和陀螺的零偏。则式(1)表示的非线性系统可以写为:

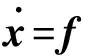
(3)

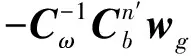
1.1.2 线性误差模型

惯导在小角度近似下的线性误差模型在文献[10-12]已有详细推导,这里直接对式(1)进行小角度线性化,结果如下:

(4)

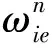
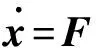
(5)

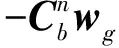
1.2 测量模型

1.2.1GPS有效时

当GPS有效时,采用GPS输出的速度和位置作为观测量[11],观测方程如下:

(6)

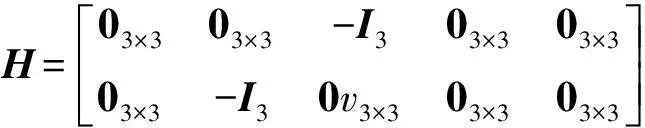
1.2.2GPS无效时

在GPS信号失效的情况下,引入车辆的运动学约束来抑制导航系统的误差[14]。假定车辆没有侧滑并且在平坦的道路行驶,这在大多数城市中都是合理的。如果满足这两个假设,车辆的侧向速度和天向速度的真实值为0,如图1所示。此时可以把这两个值看作车辆的虚拟测量值[15]。

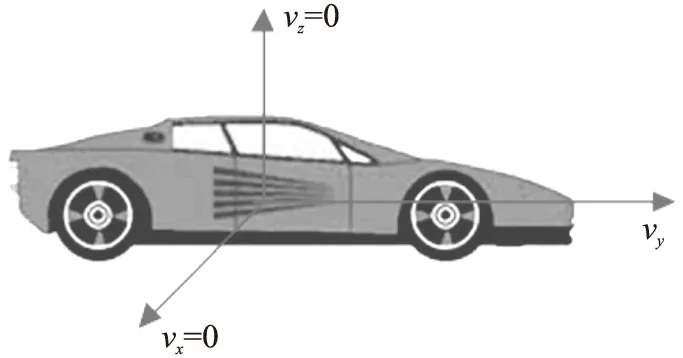
图1 车辆运动学约束示意

假设IMU的测量轴和车辆的右前上方向完全重合,则车辆速度在载体系投影的理论值为:

(7)

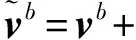
(8)

式(7)和式(8)作差可得:

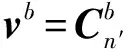
(9)

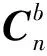
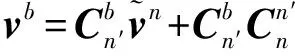
(10)

可以简记为

z=h(x,t)

(11)

(12)

测量噪声的引入是由于考虑到IMU的测量轴并不可能完全重合与车辆的右前上方向,当IMU的y轴与车辆前向有2°～3°的安装误差并且车辆以18 m/s～20 m/s的速度前行时,会在侧向和天向造成1 m/s的误差[14];并且车辆的上下坡或者转弯造成的影响也会引起相应的误差。

当α足够小时,对式(10)做线性化近似可得:

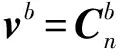
(13)

式中:vn×代表详细vn的斜对称阵。上式与文献[8]中结果一致,说明了本文推导的正确性。考虑到低精度的IMU在GPS失效时精度下降很快,因此本文在GPS失效时段将系统看作非线性,因此通过非线性滤波的手段对参数进行估计,下面介绍UKF滤波。

2 滤波算法

MEMS-IMU的低精度导致在GPS丢失时段系统有较强的非线性,传统的KF滤波算法不再适用。文献[16]从非线性均值和方差的传播的角度出发,通过UT(Unscented Transformation)变换直接进行传播,避免了非线性函数线性化近似,能够获得有比EKF(Extended KF)更高的精度[17]。文献[18-19]对噪声属于加性噪声的情况进行了简化,由于本文中系统噪声和测量噪声都是加性噪声,可以使用简化的UKF进行滤波,步骤如下:

状态初始化:

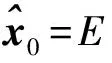
(14)

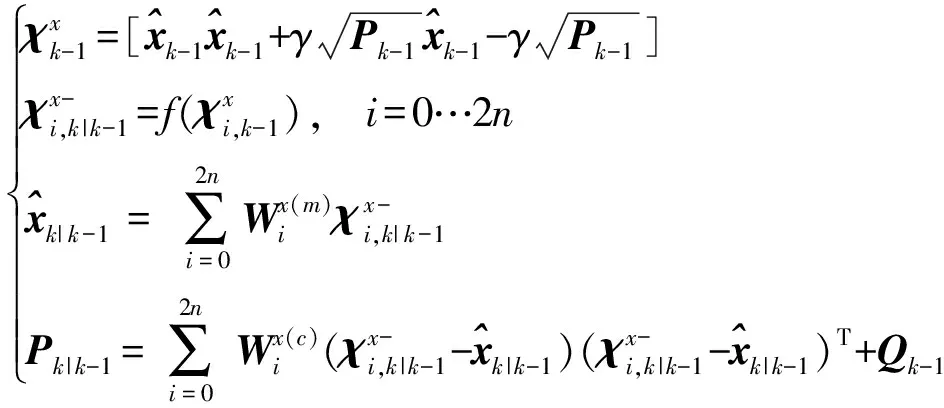
(15)

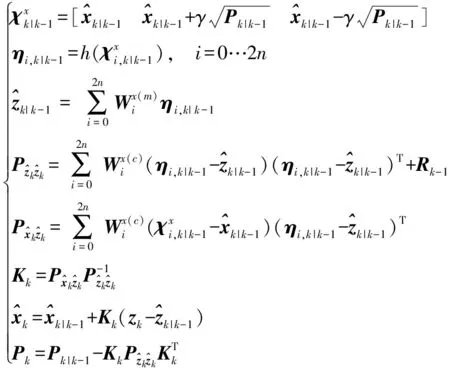
(16)

其中:

(17)

组合系统结构如图2和图3所示。

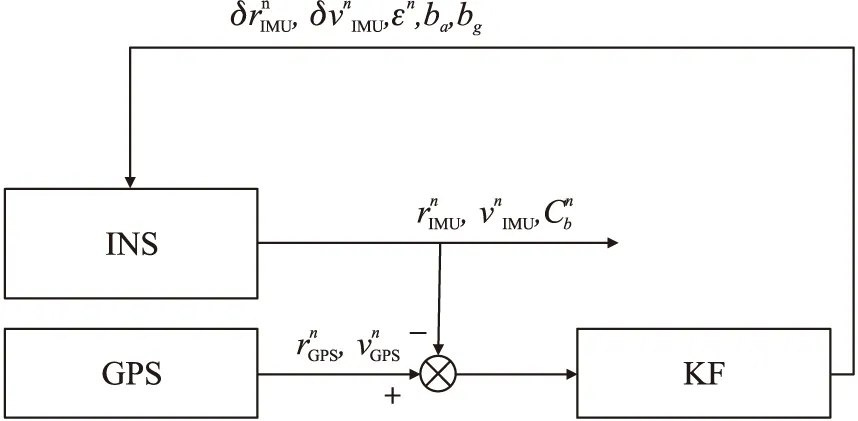
图2 GPS有效时的系统结构

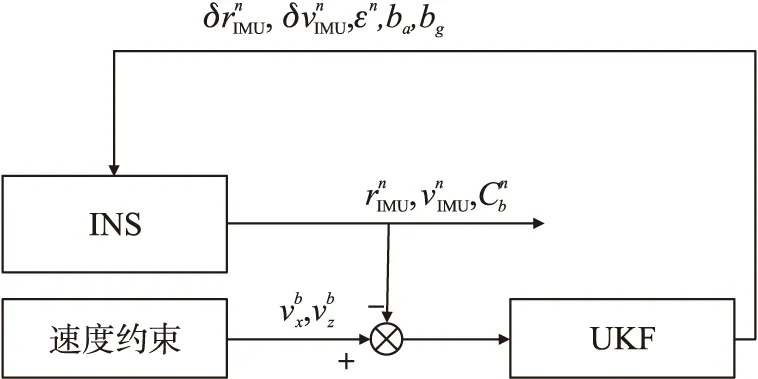
图3 GPS无效时的系统结构

3 车载实验

车载实验中,MEMS-IMU选用的是ADIS16375型三轴集成IMU,数据输出率为200Hz,陀螺和加速度计初始零偏分别为±1°/s和±16mg;GPS接收机为u-blox的NEO-6M定位模块,采样频率为1Hz,定位精度为2.5m,测速精度为0.1m/s;控制器为STM32F103型ARM芯片。采用和芯星通的UR370三频高精度接收机提供基准,该接收机采用双天线RTK(Real-TimeKinematic)测量方法,结合基准站可实现流动站厘米级的定位精度;此外,双天线差分可提供姿态角信息,沿车轴纵向安装两个天线,可输出车体的俯仰角和偏航角,姿态角精度由两个天线间的基线长度决定,基线长度越长,定姿精度越高。试验中的基线长度约为1m,定姿精度为0.5°左右。系统实物照片如图4所示。

图4 实验设备

收集跑车实验的数据做事后处理,截取持续120s的跑车数据,在第60s～100s时间段人为设置数据遮挡40s,在GPS有效阶段采用图2所示的闭环松组合结构,当GPS失效时引入速度约束的虚拟观测,结构如图3所示。首先考察引入速度约束对导航性能的改善情况,再将线性速度约束算法和本文提出的非线性速度约束算法作对比。其中卡尔曼滤波的Q阵值根据AID16375数据手册中陀螺和加计的噪声设置,R阵的值根据GPS速度和位置误差的值设置。

如图5所示为添加线性速度约束前后的导航结果对比,由图可知,当在60s～100s期间引入GPS阻断时,引入的线性速度约束可以较好地提升导航性能,由于此问题已在文献[10]中详细讨论,此处不再画出具体的位置和姿态的误差图。

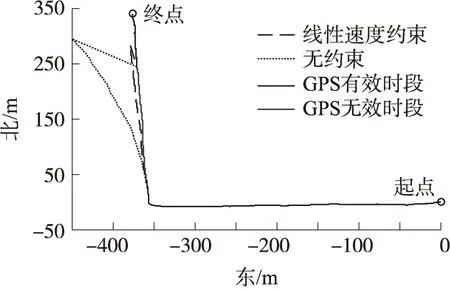
图5 约束前后轨迹对比

如图6～图11所示为非线性速度约束与线性速度约束的导航性能对比,由图可知,与线性速度约束算法相比,在GPS失效的40s中,非线性速度约束算法精度有较大提高,其中东向、北向和天向的最大位置误差分别减小了约42%、67%和21%,由于改进的非线性约束模型在GPS失效时能够做出更准确的估计,所以位置误差的发散得到抑制,非线性速度约束算法的姿态精度也高于线性速度约束算法;更重要的是,在GPS信号恢复后(100s之后),前者能迅速收敛到真值附近,而后者则不能,这是因为在在GPS失效期间造成的惯导姿态误差已经不是小量,小角度假设下的线性模型已经不再适用,线性传播下的状态和协方差也不能准确描述系统信息,而非线性模型和滤波算法则较好地提高了导航性能。由于车载实验环境的复杂性,为了进一步验证改进算法的有效性,选取另一段跑车轨迹,屏蔽其10s～50s的信号(转弯部分考虑在内)。

从图12可以看出改进算法的位置误差明显减小,此处不再画出,下面画出姿态误差,如图13和图14所示。

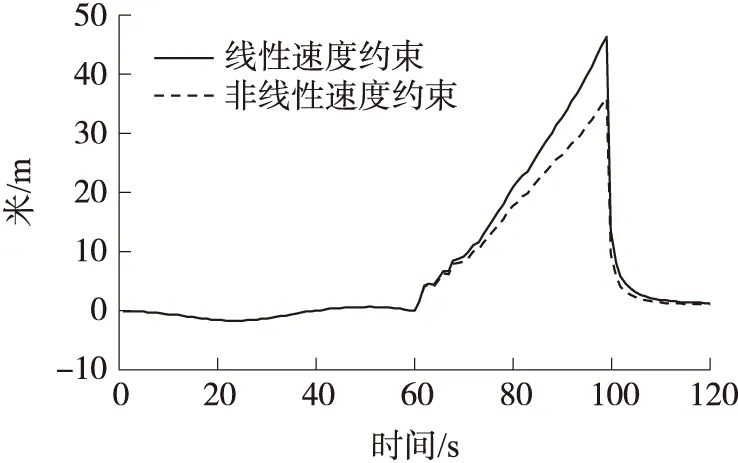
图9 天向位置误差对比

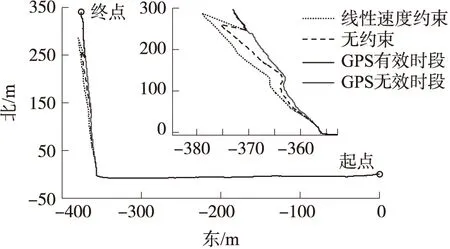
图6 轨迹对比图

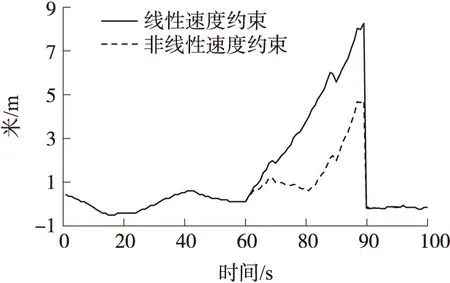
图7 东向位置误差对比

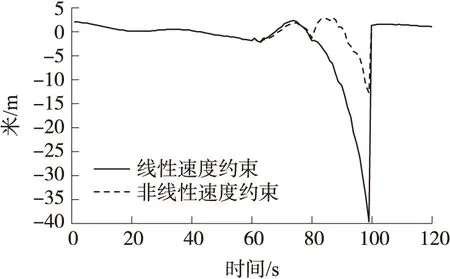
图8 北向位置误差对比

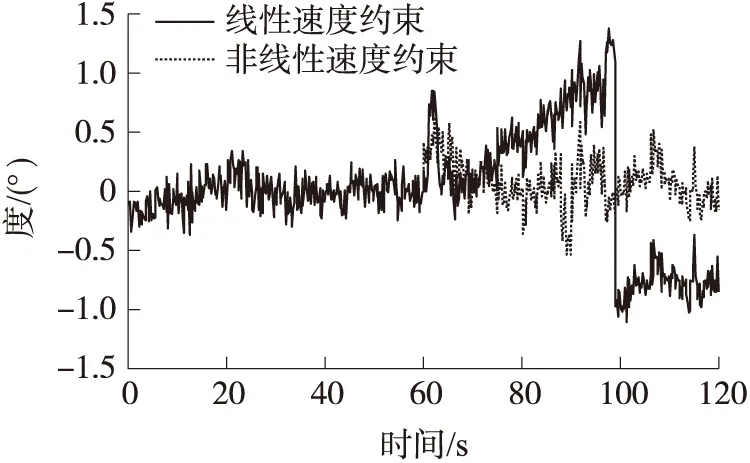
图10 俯仰角误差对比

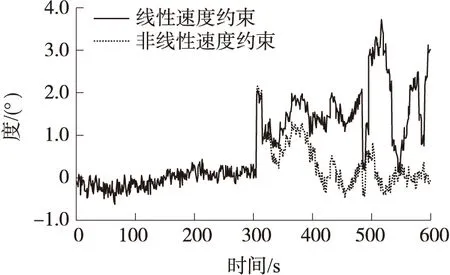
图11 偏航角误差对比

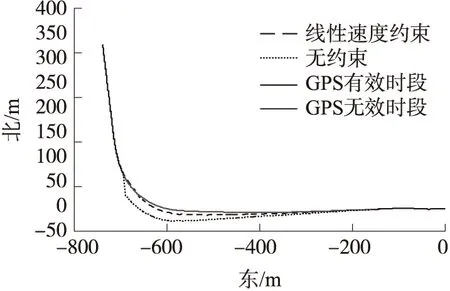
图12 轨迹对比

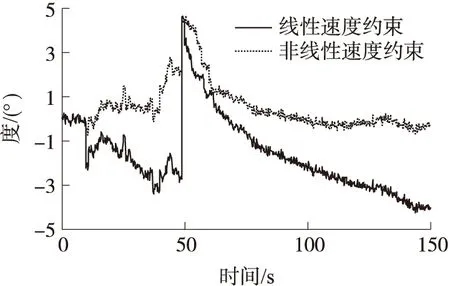
图13 偏航角误差对比

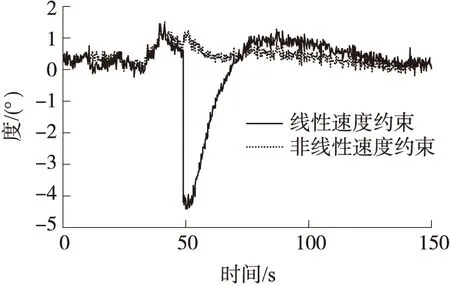
图14俯仰角误差对比

列出两组实验的最大姿态误差如表1所示。

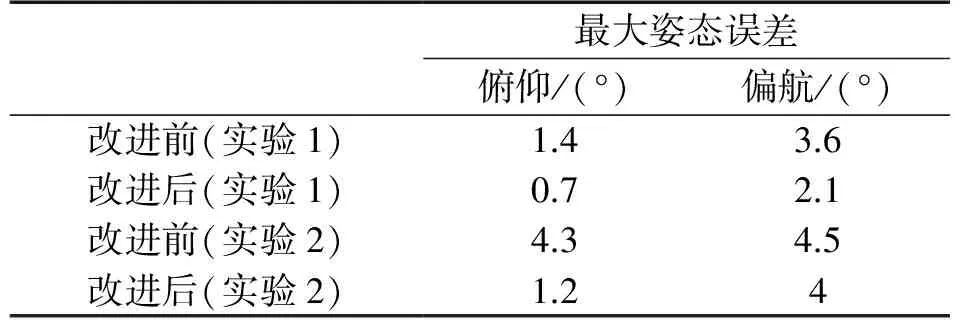
表1 最大姿态误差对比表

由于图中位置误差比较明显,不再列出。

从图中可以看出在转弯时车辆动态较大,低精度的IMU带来非线性更加明显,信号恢复后俯仰角需要更长的时间收敛到正确状态,并且直线运动时偏航角可观性较差,使其更加难以恢复到真值;改进的算法能够明显抑制误差发散,有利于组合导航性能的提升,进一步验证了算法的有效性。

6 结论

本文以车载组合导航为研究对象,当GPS失效时,假设车辆天向和侧向速度为零,引入速度方程作为虚拟观测,并用UKF滤波进行非线性估计。车载实验结果表明,本文提出的非线性速度约束方法精度高于线性速度约束方法,并且在GPS重获信号时也能够保证状态快速收敛到真值,提高了车载导航在GPS失效时的性能。后续研究中可以加入里程计,引入前向的速度约束,进行更高精度的组合导航。

[1] 牛小骥,旷俭,陈起金. 采用MEMS惯导的小口径管道内检测定位方案可行性研究[J]. 传感技术学报,2016,1:40-44.

[2] 吴利青,徐德辉,熊斌. 基于MEMS技术的双凸台微型热电能量采集器的仿真和制备[J]. 传感技术学报,2016,3:305-312.

[3] Zhang B,Chu H,Sun T,et al. Error Prediction for SINS/GPS After GPS Outage Based on Hybrid KF-UKF[J]. Mathematical Problems in Engineering,2015.

[4] Ilyas M,Yang Y,Qian Q S,et al. Low-Cost IMU/Odometer/GPS Integrated Navigation Aided with Two Antennae Heading Measurement for Land Vehicle Application[C]//Control and Decision Conference(CCDC),2013 25th Chinese. IEEE,2013:4521-4526.

[5] Godha S. Performance Evaluation of Low Cost MEMS-Based IMU Integrated with GPS for Land Vehicle Navigation Application[M]. Library and Archives Canada Bibliothèque et Archives Canada,2006.

[6] Zhang T,Xu X. A New Method of Seamless Land Navigation for GPS/INS Integrated System[J]. Measurement,2012,45(4):691-701.

[7] Chen L,Fang J. A Hybrid Prediction Method for Bridging GPS Outages in High-Precision POS Application[J]. Instrumentation and Measurement,IEEE Transactions on,2014,63(6):1656-1665.

[8] Hasan A M,Samsudin K,Ramli A R,et al. Automatic Estimation of Inertial Navigation System Errors for Global Positioning System Outage Recovery[J]. Proceedings of the Institution of Mechanical Engineers,Part G:Journal of Aerospace Engineering,2011,225(1):86-96.

[9] Yan G,Yan W,Yan W,et al. A SINS Nonlinear Error Model Reflecting Better Characteristics of SINS Errors[J]. Xibei Gongye Daxue Xuebao,2009,27(4).

[10] Shin E H,El-Sheimy N. Accuracy Improvement of Low Cost INS/GPS for Land Applications[M]. National Library of Canada=Bibliothèque nationale du Canada,2003.

[11] Titterton D,Weston J L. Strapdown Inertial Navigation Technology[M]. IET,2004.

[12] Groves P D. Principles of GNSS,Inertial,and Multisensor Integrated Navigation Systems[M]. Artech House,2013.

[13] Wu Z,Yao M,Ma H,et al. Improving Accuracy of the Vehicle Attitude Estimation for Low-Cost INS/GPS Integration Aided by the GPS-Measured Course Angle[J]. IEEE Transactions on Intelligent Transportation Systems,2013,14(2):553-564.

[14] Godha S. Performance Evaluation of Low Cost MEMS-Based IMU Integrated with GPS for Land Vehicle Navigation Application[M]. Library and Archives Canada=Bibliothèque et Archives Canada,2006.

[15] 徐田来. 车载组合导航信息融合算法研究与系统实现[D]. 哈尔滨:哈尔滨工业大学,2007.

[16] Julier S J,Uhlmann J K. Unscented Filtering and Nonlinear Estimation[J]. Proceedings of the IEEE,2004,92(3):401-422.

[17] Zhang P,Gu J,Milios E E,et al. Navigation with IMU/GPS/Digital Compass with Unscented Kalman Filter[C]//Mechatronics and Automation,2005 IEEE International Conference. IEEE,2005,3:1497-1502.

[18] Kolås S,Foss B A,Schei T S. Constrained Nonlinear State Estimation Based on the UKF Approach[J]. Computers and Chemical Engineering,2009,33(8):1386-1401.

[19] Van Der Merwe R. Sigma-Point Kalman Filters for Probabilistic Inference in Dynamic State-Space Models[D]. Oregon Health and Science University,2004.

姜博文(1991-),男,硕士研究生,主要研究方向为组合导航;

王可东(1975-),男,博士,副教授,硕士生导师,主要研究方向为卫星/惯性组合导航、天文/惯性组合导航、最优滤波算法和地形匹配算法等,wangkd@buaa.edu.cn。

Algorithm Design for a Low-Cost Vehicle Integrated Navigation System in the GPS Outage

JIANGBowen,WANGKedong*

(School of Astronautics,Beihang University,Beijing 100191,China;)

The performance of a micro-electro-mechanical system-inertial measurement unit(MEMS-IMU)/global positioning system(GPS)integrated system will be degraded significantly due to the poor performance of the MEMS-IMU if the GPS signals are blocked by the buildings. To resolve this problem,the up and side vehicle velocity constraints are modelled as the virtual measurements. The nonlinear velocity measurement equations are derived without the small angle approximation if the nonlinearity due to the low accuracy of the MEMS IMU is taken into account in the GPS outage. The Unscented Kalman Filter(UKF)is employed to improve the integration accuracy. The vehicle test results show that the proposed nonlinear algorithm with the velocity constrains can improve the integration accuracy significantly in the GPS outage and converge quickly when the GPS signals is reacquired.

GPS;MEMS;UKF;integrated navigation;inertial navigation system

2016-07-05 修改日期:2016-11-02

V249.32

A

1004-1699(2017)03-0412-06

C:7230

10.3969/j.issn.1004-1699.2017.03.014