基于二阶矢量位的线圈横向移动三维涡流理论建模
姜盈盈,姚丽芳,朱学平,陈 宇,朱毅晨,吕春峰
(1.上海市计量测试技术研究院,上海 201203;2.上海海洋大学工程学院,上海 201306)
基于二阶矢量位的线圈横向移动三维涡流理论建模
姜盈盈1*,姚丽芳1,朱学平1,陈 宇1,朱毅晨1,吕春峰2
(1.上海市计量测试技术研究院,上海 201203;2.上海海洋大学工程学院,上海 201306)
针对电涡流传感器探头线圈相对导体横向移动时阻抗变化的涡流问题,以二阶矢量位电磁理论为基础,在直角坐标系下,推导出线圈相对导体横向移动时的阻抗及阻抗变化量公式,建立其电磁场三维涡流理论模型,且通过试验验证了模型的正确性。使用Mathematice软件建立模型计算分析线圈几何尺寸(内径、厚度、线宽、线间距)对传感器灵敏度的影响,为合理选择线圈参数和优化传感器性能提供参考。
电涡流传感器;线圈涡流分析;二阶矢量位;几何参数
电涡流传感器是20世纪70年代兴起的一种以电涡流效应为原理的无损、非接触位移、振动检测装置,具有灵敏度高、抗干扰能力强、不受介质影响、结构简单等优点,是大型旋转机械故障诊断与状态检测的标准配置传感器。它由探头(传感头)、变换器(前置器)和连接电缆组成。在交变电流激励下,利用探头线圈和被测体间的磁场能量耦合实现对被测量的检测。对于以位移为检测量的传感器,希望有较大的线性范围和较高的灵敏度。电涡流传感器的灵敏度和线性范围主要受线圈磁场分布影响[1],而线圈磁场分布又受其形状和几何参数直接影响[1-3],因此研究线圈形状及其几何参数对传感器性能的影响具有现实意义。国内外学者在这方面也做了大量研究:文献[4]考察了圆形线圈、矩形线圈以及三角形线圈的厚度、外径对线圈磁场分布的影响;文献[5]针对含铁氧体磁芯的电涡流传感器考察了铁氧体直径、磁导率、线圈内外径比、线圈匝数、提离高度、线径及磁芯高出线圈的高度对传感器灵敏度的影响;文献[6]考察了涡流渗透深度与被测体电导率、磁导率、检测频率、线圈形状及激励磁场间的关系。
本文在前人研究的基础上,针对线圈对导体横向移动的电磁涡流问题进行研究,借助于二阶矢量位电磁场理论建立线圈相对导体横向移动的电磁涡流理论模型,并推导出线圈阻抗求解公式,继而线圈几何尺寸对传感器灵敏度的影响。
1 二阶矢量位电磁场理论
B=×A
(1)
由比奥-沙伐(Biot-Savart)定律可知,磁场中任意一点的磁感应强度为:
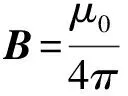
(2)
式中:Idl为电流回路C的线电流元,R为该线电流元至场点的距离。
根据亥姆霍兹(Helmholtz)定理[7-8]可知,要唯一地确定一个矢量场函数,不仅要确定其旋度,而且还需要给定其散度。本论文中,选定·A=0,称之为库仑规范(Coulomb’sgauge),并结合式(1)和式(2),于是可以得到矢量磁位A的表达式为:
(3)
××A=μJ
(4)
2A=-μJ
(5)
在自由电流密度J=0区域,方程(5)变成:
2A=0
(6)
即为矢量磁位的拉普拉斯方程。在忽略位移电流的条件下,关于矢量磁位的泊松方程(5)可以写成:
2A=jωμσA
(7)
式中:ω=2πf为角频率,f为线圈激励频率。令k2=-jωμσ为电磁场中介质的传播常数,则方程可以用亥姆霍兹方程的形式写出:
2A+k2A=0
(8)
使用矢量磁位时,必须保证选取的坐标系得到3个形式相同的分量,即其只能在直角坐标系中使用,不能用于柱坐标系或者球坐标系中。为了解决这个问题,对矢量磁位A进一步分解,引入二阶矢量位[9],矢量磁位的零散度表达式:
A=×W
(9)
式中:W为二阶矢量位,可以由两个标势函数求导得到。
在电磁场研究中,为了满足边界条件,简单的方法是把W分解为两个相互垂直的分量,每个分量由一个标势函数导出,即:
W=uWa+u×Wb
(10)
式中:u为坐标系中的任意坐标轴方向单位矢量,Wa与Wb是矢量W的两个标势函数。通过式(10)分解后Wa与Wb满足拉普拉斯方程或亥姆霍兹方程:
2Wa,b+k2Wa,b=0
(11)
二阶矢量位可运用于三维电磁场的涡流分析[10-11]中,用该方法可以推导出线圈阻抗以及被测导体表面涡流分布的解析表达式。
2 基于二阶矢量位的三维涡流问题理论建模
2.1 直角坐标系下二阶矢量位及其场量表达式
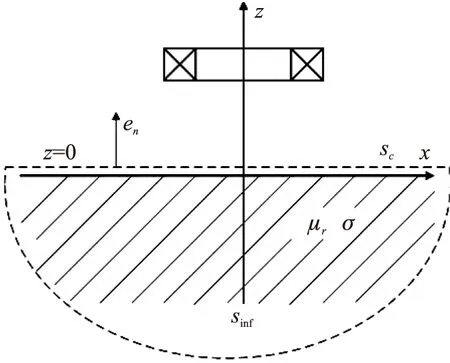
涡流栅位移传感器单线圈通用模型可用图1来表示,在直角坐标系下对传感器进行理论建模。在图中检测线圈位于各项同性的铜质无限大导体正上方,坐标轴z与线圈轴线重合。线圈通入正弦交流电流激励,其表示形式Iejωt(ω=2πf,f为电流激励频率)。无限大导体的磁导率为μr,电导率为σ。
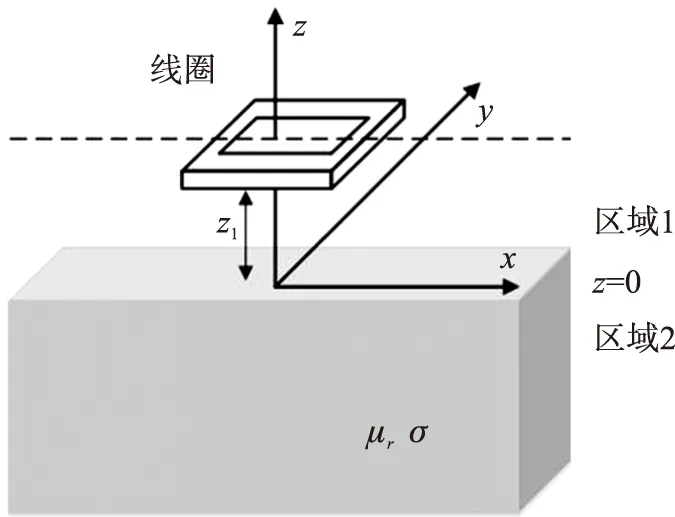
图1 涡流栅位移传感器单线圈通用模型
以z=0平面为分界面,将整个空间区域分成两个区域:①区域1:线圈与空气组成的无限大空间;②区域2:无限大导体空间。
在直角坐标系中,选取z坐标轴方向的单位矢量ez来对二阶矢量位函数进行分解,其表达式为
W=ezWa+ezWb
(12)
式中:Wa与Wb分别为横电(TE)标势函数与横磁(TM)标势函数。可以利用表达式(12)中两个标势函数Wa与Wb通过关系式A=×W与B=××W将矢量磁位A与磁感应强度B在直角坐标系下的各个分量表示出来:
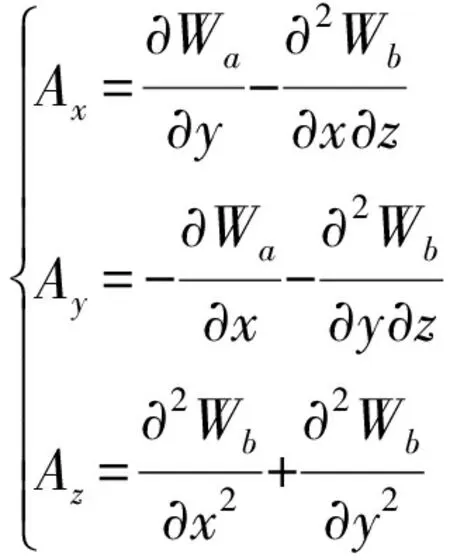
(13)
(14)
式中:k2=jωμ0μrσ为介质传播常数。由表达式(14)可以看出,在非导体区域中磁感应强度B仅与一个标势函数Wa有关,因此可用该函数的梯度将其表示出来:
B=
(15)
2.2 电磁场方程建立及其通解
横电和横磁两个标势函数Wa与Wb在空气区域或导体区域满足拉普拉斯方程或者亥姆霍兹方程:
(16)
根据分离变量法可知拉普拉斯方程通解为:
X(x,y)=[A1sin(kxx)+
A2cos(kxx)][B1sin(kyy)+B2cos(kyy)]
(17)
和
Z(z)=C1ekzz+C2e-kzz
(18)
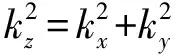
由图1可知,自然边界条件为:
(19)
式中:x=hx为x轴正方向边界,y=hy为y轴正方向边界,hx和hy取线圈外半径的20倍以上。
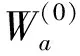
[C(s)(umn,vmn)eγmnz+D(ec)(umn,vmn)e-γmnz]
(20)
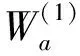
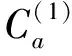
(21)
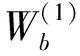
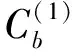
(22)
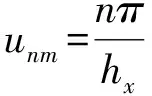
由于区域2中z轴负半轴趋于负无穷大,所以表达式和可以改写为:
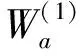
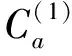
(23)
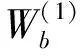
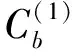
(24)
式(20)、式(23)和式(24)是标势函数在不同区域的通解表达式。
2.3 边界条件下的通解未知系数求解
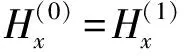
(25)
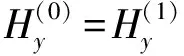
(26)
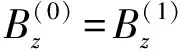
(27)
将式(20)、式(23)和式(24)代入至上述3个等式中可以得到如下方程组:
(28)
由上节的分析可知,只要确定了激励源系数C(s)(umn,vmn),通过求解该方程组就可以通过该激励源系数将其余3个未知系数线性地表示出来:

(29)
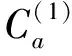
(30)
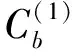
(31)
将上述系数表达式代入式(20)、式(23)和式(24)中,并对其就级数即可得到各个区域内两个标势函数的解析表达式:
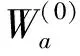
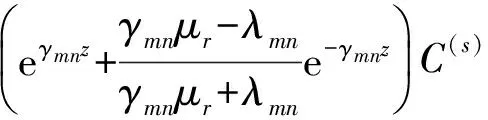
(32)
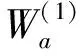
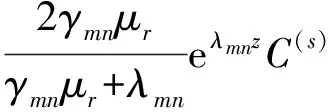
(33)
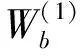
(34)
由式(34)可知,横磁标势函数Wb在整个求解区域内都为0,因此,整个问题可以仅用一个横电标势函数Wa来描述。横磁标势函数Wb在整个求解区域内都为0,表示了在半无限大导体区域内其感应电涡流密度的z方向分量为零。
式(32)和式(33)表明,在确定激励源系数C(s)下,即可获得横电标势函数Wa,也即可以得到磁感应强度。
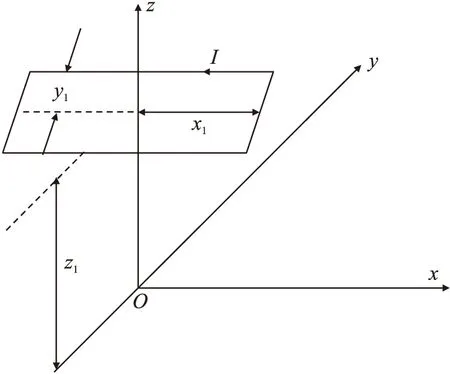
图2 单匝矩形线圈
2.4 矩形线圈激励源系数的确定
线圈激励源系数C(s)与线圈属性以及其在坐标系中的方位有关,从原理上说线圈激励源系数适用于任意形状、任意角度放置的激励线圈。
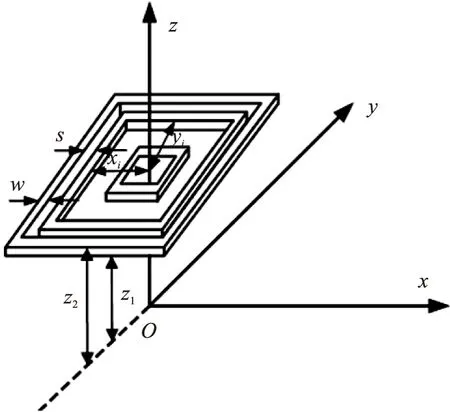
首先从单匝矩形线圈结构开始分析,如图2所示为单匝矩形线圈水平放置于直角坐标系中,线圈中心坐标为(0,0,z1),线圈的长度和宽度分别为2x1和2y1,线圈激励电流为I。
磁场中除线圈外任意一点的磁感应强度B可通过毕奥-沙伐定律来表示:

(35)
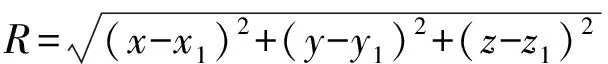
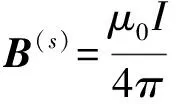
(36)
B(s)=
(37)
将磁感应强度的表达式B=(∂Wa/∂z)与表示式(37)相比较,即可列写出关于激励源标势函数的表达式:
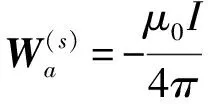
(38)
式(38)对于图2中水平放置的单匝矩形线圈有ds=ezdx1dy1,而关于1/R表示式在直角坐标系中可以写成如下形式:

(39)
将式(39)代入至式(38)中得到:
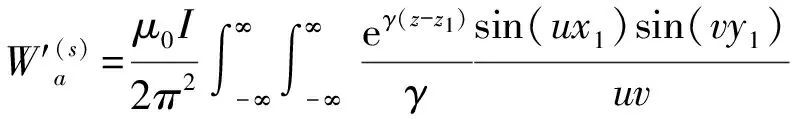
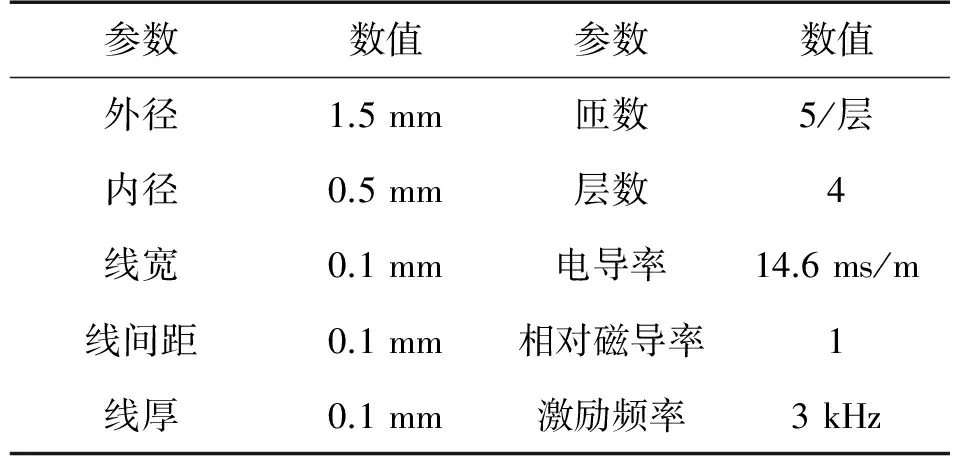
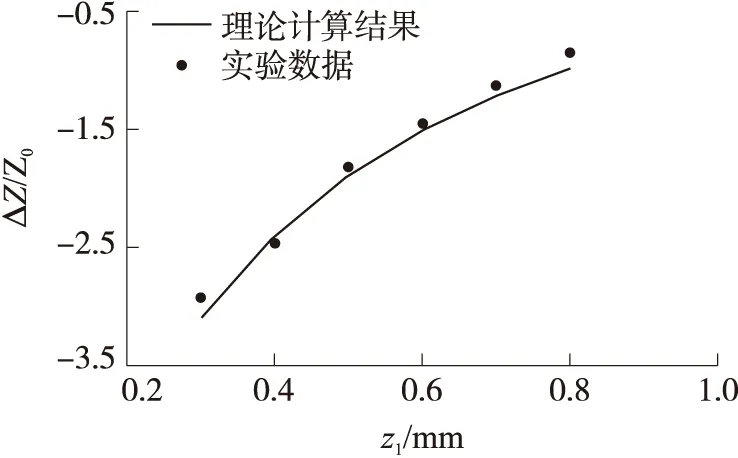
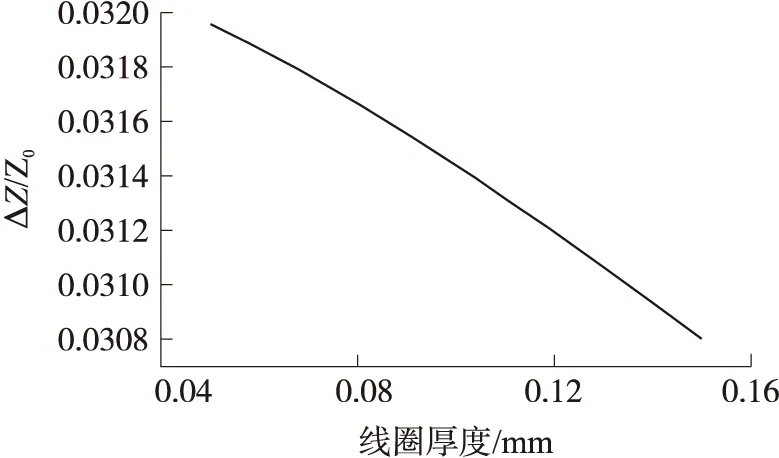
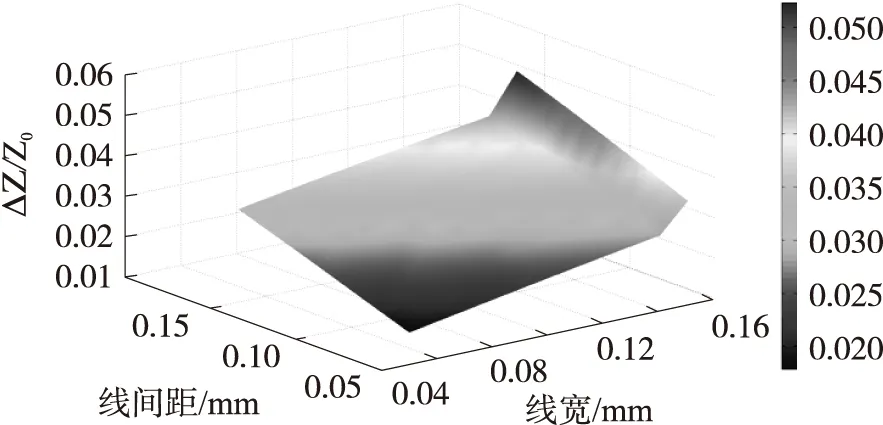
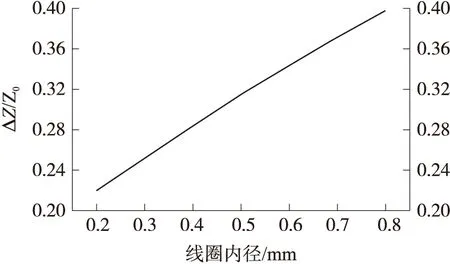
ej(ux+vy)dudvz (40) 式(40)即为单匝矩形线圈的激励源标势函数表达式。如果线圈的中心移动到(x′,y′,z1),则将因子e-j(αx′+βy′)添加到式(40)即可。 图3 多匝平面螺旋线圈简化模型 在实际运用中的电涡流传感器线圈通常为多匝平面螺线型线圈,其中每匝线圈都是有一定宽度和厚度的,所以可以将其简化为多个矩形截面的矩形线圈组合,其结构形状如图3所示。 现在先计算具有矩形截面的矩形线圈的激励源标势函数Wa,该线圈的结构形状和参数如图4所示。 图4 具有矩形截面的矩形环 图4中线圈轴线与z轴重合;xi、yi分别对应在长、宽方向上线圈内边缘至z轴的距离;w为线圈宽度;z1、z2则分别为线圈底面和顶面至z=0平面的距离。对于该种类型的线圈的激励源标势函数和系数 表达式的求解则可在单匝线圈的基础之上运用叠加的方法求解得到。 假设流过线圈每处的电流密度的幅值和相位均保持不变,忽略线圈绕组中的趋肤效应和层间耦合效应,含矩形截面的矩形柱线圈的激励源标势函数可通过单匝矩形线圈的激励源标势函数用积分表达式表示出来: (41) 结合图4中标注的线圈尺寸参数,上式可进一步写成: (42) 将表达式(40)代入式(42)中得到: (43) 式中: 表达式(43)是单匝矩形线圈的激励源标势函数,对其进行叠加即可以得到多匝线圈的激励源标势函数: (44) 式中:N为线圈的匝数。 激励源标势函数在z=0平面上求解时,是在x=hx,y=hy的区域内求解的,其中hx和hy的取值范围为大于20倍的线圈外径。所以可以将用级数形式求解激励源标势函数,即将式(44)转换为级数形式,如下式: (45) 此时,我们得到了级数形式的激励源标势函数。将式(45)与边界条件下的通解表达式(32)作对比,就可以得到线圈的激励源系数的解析表达式: C(s)(umn,vmn)= (46) 在得到激励源系数表达式后,即可根据式(29)~式(31)将其余的未知系数表示出来,并将其代入相应的标势函数中就可推导出电磁场中的各种场量的解析表达式。 2.5 线圈阻抗求解 当线圈下方无导体存在时,线圈交流阻抗的计算通过线圈上的电压和电流的关系来确定,即Z0=V/I。此时线圈上的电压计算表达式为: V=jω∫SB·ds (47) 对于图4中的矩形柱线圈来说,我们仍可用叠加的方法,通过计算垂直穿过线圈的磁感应强度Bz来计算该线圈中的电压。此时式(47)可改写为: (48) (49) 式中:X0=ωL0为线圈初始交流感抗,L0为线圈初始电感。而对于线圈电阻的计算方法,通常在激励频率小于10MHz时可根据线圈尺寸以及电导率等参数按照直流电阻计算公式得到: (50) 式中:NLc为N匝矩形柱线圈导体总长度,σc为线圈制作材料的电导率。因此在实际的线圈制作过程中,为了提高线圈品质因数,需将线圈材质、绕制方法等问题考虑进去,从而达到减小线圈电阻提高品质因数的目的。 图5 线圈阻抗变化值求解区域分析 当传感器检测线圈位于导体上方时,由于导体内涡流效应的作用,将会对线圈阻抗产生影响。设Z0为检测线圈下方无导体时的阻抗值,称之为自由空间阻抗;而当线圈下方有导体存在时,线圈阻抗值变为Z;二者的差值ΔZ=Z-Z0即为受导体感应电涡流引起的线圈阻抗变化值ΔZ。对于图5线圈位于无限大导体正上方时的情形,线圈阻抗变化值的求解表达式为: (51) 式中:SC表明顶面为平面导体表面z=0,且包含半无限大导体区域Sinf的一个无限大闭合曲面,在顶面z=0处,其单位法向矢量en与z轴方向一致;E′与B′分别表示导体存在时的电场强度矢量和磁感应强度矢量;E(s)与B(s)则表示没有导体存在时的电场强度矢量和磁感应强度矢量。 E(S)×B′=-××E(S) (53) 同理对于式(52)积分式中的第2项经化简得到: (54) 将式(53)、式(54)代入至式(51)得到: (55) 式中:有关磁感应强度矢量B(s)、B′也可通过标势函数表示出来: (56) ΔZ= (57) (58) 至此,经过严格的数学推导,我们得到了关于传感器三维涡流场中待求物理量如感应电涡流密度、磁感应强度、线圈阻抗变化值等的闭合解析表示式,其计算结果可通过相关的工具软件如MATLAB、Mathematica等求解得到。 3.1 理论模型实验验证 为了计算出上述阻抗求解表达式,采用Mathematice软件对线圈初始阻抗表达式(49)和线圈阻抗变化表达式(58)。线圈尺寸如表1所示。 表1 线圈以及导体相关参数 根据上述参数计算线圈在导体正上方横向移动时的电感变化量,如图6所示,由图可知理论模型计算的电感变化值与实验数据基本一致,由此可知理论模型是正确的。理论模型给出了线圈几何参数(内径、线宽、线间距、线圈厚度、外径、匝数)与线圈阻抗变化量之间的关系公式,所以根据计算这些公式可以仿真出线圈几何参数对阻抗变化量的影响,有利于传感器设计初期对线圈尺寸的设计。 图6 归一化线圈电感变化曲线 3.2 线圈参数优化 影响涡流栅位移传感器[12]线圈电感线圈几何参数[13]有:内径、线宽、线间距、线圈厚度、外径、匝数等,这些参数同样对传感器信号质量也是至关重要的。根据上述理论模型,本文将讨论怎样的线圈几何参数最有利于传感器的信号质量。 根据式(46)、式(58)可以得到电感相对变化量与线圈厚度z2-z1的关系,如图7所示。由图7可知,电感相对变化值随着线圈厚度的增加近似线性减小,所以为了得到较大的电感相对变化值,可以选取厚度较小的线圈作为敏感元件。 图7 电感相对变化量与线圈厚度的关系 同样的道理可以绘制线间距和线宽对电感相对变化量的影响,如图8所示为其三维图,线间距越大电感相对变化量越大,线宽越大电感相对变化量越大,线间距对电感相对变化量的斜率比线宽小。线圈外径可以由内径、线宽和线间距确定,根据传感器设计要求,一般线圈外径尺寸会被确定,如涡流栅位移传感器的测量码道线圈外径为1.5 mm,所以在外径尺寸一定的条件下,增大线宽较小线间距更有利于获得较高的电感相对变化量。 图8 线间距和线宽对电感相对变化量的影响 线圈内径对电感相对变化量影响也是相当重要的,如图9所示为内径与电感相对变化量的关系,电感相对变化量随着内径的增加而增加,所以在条件允许的情况下,可以考虑通过提高内径来提升传感器的测量精度。 图9 线圈内径对电感相对变化量的影响 根据上述分析,可以得到如表2所示的线圈参数对电感相对变化量的影响,从表中可知内径、线间距、线宽与电感相对变化量成正比,而厚度与其成反比,其中内径对电感相对变化量的影响最大,所以在实际设计线圈时,若在线圈外径尺寸允许的条件下,可以优先考虑提高线圈内径,同时增大线圈线宽;而若在线圈外径尺寸一定的条件下,可以考虑提高线宽、减小厚度来提高传感器的灵敏度。 表2 线圈参数对电感相对变化量的影响量 本文介绍了电涡流相关电磁场基本理论,提出了一种基于二阶矢量位的矩形线圈涡流栅传感器的三维涡流理论模型,在此基础上给出了相关电磁场方程的建立及求解方法,并给出了线圈阻抗求解公式。该模型可以分析矩形线圈几何参数对线圈的阻抗特性及品质因数的影响,同时还可以用于分析矩形线圈几何参数对传感器信号的影响。文章还利用该模型对传感器信号进行分析,得出怎么样的矩形线圈几何参数更有利于提高传感器的灵敏度,所以这个结论在设计传感器线圈时,可以起到指导性的作用。 [1] Hanson J M,Bialek J,Turco F,et al. Validation of Conducting Wall Models Using Magnetic Measurements[J]. APS Physics,2016,56(10):106022-106034. [2] Wang Chunjie,Ji Shengchang,Nie Jiyu,et al. Design and Performance of a Novel Pancake Rogowski Coil for Measuring Pulse Currents[J]. Plasma Science and Technology,2011,13(6):751-756. [3] Liu G,Du J. Performance Analysis of Link Algorithm in Congestion Control[J]. International Conference on Advanced Computer Theory and Engineering,2010,3:84-87. [4] Ruan J,Xu Z. A New Model of Repulsive Force in Eddy Current Separation for Recovering Waste Toner Cartridges[J]. Journal of hazardous materials,2011,192(1):307-313. [5] Capobianco T E,Splett J D,Iyer H K. Eddy Current Probe Sensitivity as a Function of Coil Construction Parameters[J]. NDT and E International,1995,4(28):250. [6] 游凤荷,陈丹,牛龙江. 涡流三维磁场测量及实际渗透深度建模[J]. 仪器仪表学报,2002,23(4):431-433. [7] Mstl U V,Temmer M,Veronig A M. The Kelvin-Helmholtz Instability at CME-Boundaries in the Solar Corona:Observations and 2.5D MHD Simulations[J]. Astrophysical Journal Letters,2013,766(1):52-61. [8] 孙敏杰. 基于亥姆霍兹线圈的磁场探头校准研究[D]. 北京交通大学,2014. [9] 郝宽胜,黄松岭,赵伟,等. 基于二阶矢量位的矩形截面回折线圈阻抗和脉冲磁场的解析建模与计算[J]. 物理学报,2011,60(7):78103-078103. [10] Vyroubal D,Zele D. Experimental Optimization of the Probe for Eddy-Current Displacement Transducer[J]. Instrumentation and Measurement,IEEE Transactions on,1993,42(6):995-1000. [11] 郝宽胜,黄松岭,赵伟,等. 基于二阶矢量位的矩形截面回折线圈阻抗和脉冲磁场的解析建模与计算[J]. 物理学报,2011,60(7):784-793. [12] De G N,Crevecoeur G,Dupré L,et al. A DTI-Based Model for TMS Using the Independent Impedance Method with Frequency-Dependent Tissue Parameters[J]. Physics in Medicine and Biology,2012,57(8):2169-2188. [13] 范吉志,吴运新,石文泽,等. 电磁超声换能器线圈设计与提高换能效率研究[J]. 传感技术学报,2016,29(1):29-34. 姜盈盈(1988-),女,浙江绍兴人,硕士,工程师,主要研究方向为长度、温度传感器等方面研究,jiangyingying@simt.com.cn; 吕春峰(1978-),男,山东莱阳人,主要从事现代传感器与无线传感器网络的研究,博士,上海海洋大学工程学院讲师,cflv@shou.edu.cn。 Analytical Modelling for the Three-Dimensional Eddy Current About Lateral Movement of the Coil Based on Second Order Vector Potential JIANGYingying1*,YAOLifang1,ZHUXueping1,CHENYu1,ZHUYichen1,LVChenfeng2 (1.Shanghai institute of measurement and testing technology,Shanghai 201203,Chnia;2.Shanghai ocean university of engineering science and technology,Shanghai 201306,China) To study eddy current problem of impedance of eddy current sensor coil moving in transverse direction to conductor,this paper deduces the formula of the impedance and the impedance change in the Cartesian coordinate system when the relative position of coil and conductor is changed,based on second order vector potential. Three-dimensional eddy current model of ECS electromagnetic field are derived based on theabove work,and it is verified by experiments. Using Mathematice to build model,the effect of coil geometry(inside diameter,thickness,line width,line spacing)on the sensitivity and linear measurement range of ECS. Theconclusionsfrom the study provide are ference fordeter mining thecoil shapeparameters and optimizing the per for manceof ECS. eddy current sensor,analysis of coil eddy current,second order vector potential,geometricparameter 2016-07-28 修改日期:2016-11-22 TP212.1 A 1004-1699(2017)03-0425-08 C:7230 10.3969/j.issn.1004-1699.2017.03.016

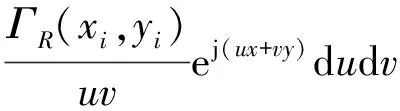
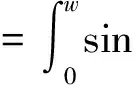
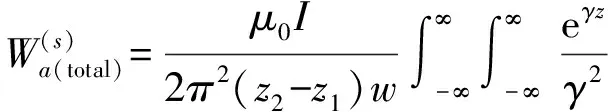
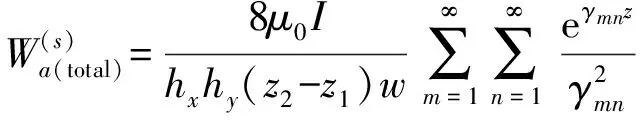
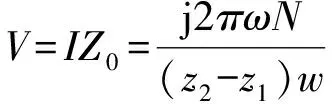
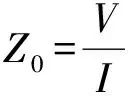
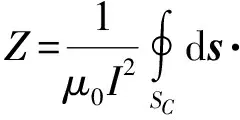
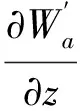

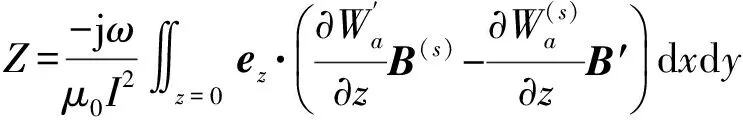
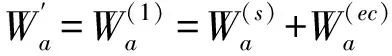
3 实验验证及线圈参数优化

4 结论总结



