基于人工蜂群优化高斯过程的运动想象脑电信号分类*

耿雪青,佘青山,韩 笑,孟 明

(杭州电子科技大学智能控制与机器人研究所,杭州 310018)



基于人工蜂群优化高斯过程的运动想象脑电信号分类*

耿雪青,佘青山*,韩 笑,孟 明

(杭州电子科技大学智能控制与机器人研究所,杭州 310018)

针对传统的高斯过程采用共轭梯度法确定超参数时对初值有较强依赖性且易陷入局部最优的问题,提出了一种基于人工蜂群优化的高斯过程分类方法,用于脑电信号的模式识别。首先,构建高斯过程模型,选择合适的核函数且确定待优化的参数。然后,选取识别错误率的倒数为适应度函数,使用人工蜂群算法搜索寻找出限定范围内可以取得最优准确率的超参数。最后,采用参数优化后的高斯过程分类器对样本分类。分别采用2008年竞赛数据集BCI Competition Ⅳ Data Set 1和2005年数据集BCI Competition Ⅲ Data Set Ⅳa对所提方法进行验证,并与支持向量机(SVM)、人工蜂群优化的支持向量机(ABC-SVM)、高斯过程分类(GPC)方法进行比较,实验结果表明了所提方法的有效性。

脑电信号,高斯过程分类,人工蜂群,运动想象

脑-机接口技术BCI(Brain Computer-Interface)是不依赖于外周神经和肌肉系统,直接在大脑和计算机或其他外部设备建立交流和控制通路的人机交互系统[1]。BCI技术已经引起了国内外研究学者的广泛关注,在助残、康复、辅助控制、娱乐等领域有很好的应用前景。模式分类是脑-机接口的关键技术之一,由于脑电信号具有微弱性、复杂性和非平稳性等特点,有效、快速地区分不同意识活动的成分是脑电信号处理领域面临的严峻挑战。因此,探索有效的分类方法以提高脑电模式分类精度仍然具有重要意义。

目前,国内外研究者提出很多脑电模式分类的方法,主要包括线性判别分析(LDA)[2]、人工神经网络(ANN)[3]、支持向量机(SVM)[4]等。实践证明,LDA实现简单,计算量小,分类速度快,在处理类别较少的EEG数据时可取得较好的分类效果。但在处理小样本问题时,容易陷入维数灾难[2]。ANN的神经元连接比较灵活,所以该方法有较高的拟合度和较强的自适应性,它在解决非线性复杂问题时表现出较大的优越性,但是该方法容易陷入局部最小,存在过学习现象[3]。SVM以统计学习理论为基础,巧妙地引入了核函数,避免了维数灾难现象,且能有效地解决小样本、非线性问题[4]等,因此在脑电信号分类中得到广泛的应用[4-6]。

2006年,Rasmussen等人[7]通过理论研究和数值实验分析,正式提出了高斯过程机器学习方法。高斯过程是基于贝叶斯框架的新型核学习机,除了对于高维数、小样本、非线性等复杂问题具有较好适应性的优点外,它还具有容易实现、预测输出具有概率意义的优点[8]。所以该方法一经提出,就在机器学习领域引起广泛关注,并被用于回归和分类[8-9],但在脑电信号分类研究中应用较少。另外,高斯过程的预测和分类精度都依赖于超参数的选择,传统的高斯过程采用共轭梯度法确定超参数,其效果依赖于初值,易陷入局部最优。为此,文献[10]将遗传算法与高斯过程回归算法相结合,用于隧道围岩变形预测,提高了预测精度。文献[11]采用粒子群算法优化高斯过程回归模型的超参数,用于滑坡位移时序的预测,取得了较好的效果。文献[12]采用人工蜂群算法搜索高斯过程回归模型的最优超参数,用于海上远程精确打击体系作战效能评估中。

针对上述情况,本文基于智能优化与机器学习相集成的思想,提出了一种基于人工蜂群优化高斯过程的运动想象脑电信号分类算法。首先通过实验对比了遗传算法、粒子群算法、人工蜂群算法的性能特点,然后将综合性能较优的人工蜂群算法与高斯过程分类算法相结合,用于脑电信号的特征分类中,最后分别在两届脑电公开竞赛数据集上进行实验测试,验证了所提算法的有效性。

1 实验数据

本文分别采用2008年第四届脑-机接口竞赛数据BCI Competition Ⅳ Data Set 1和2005年第3届竞赛数据BCI Competition Ⅲ Data Set Ⅳa进行实验分析。

①BCI Competition Ⅳ Data Set 1。该数据集由Berlin BCI研究组提供[13]。4名受试者(a,b,f和g)按照要求执行运动想象任务,共采集59个通道的脑电信号数据,采样频率为100 Hz。每个受试者按照电脑屏幕的提示执行左手、右手、单或双脚3种运动想象任务中的两类。具体而言,受试者a和f想象左手、脚运动,受试者b和g想象左手、右手运动。每个受试者执行200次实验,每类任务执行100次。

②BCI Competition Ⅲ Data Set Ⅳa。该数据集也由Berlin BCI研究组提供[14]。5名受试者(aa,al,av,aw和ay)根据显示器提示完成右手和脚的运动想象任务。采用118个通道记录脑电信号数据,采样频率为100 Hz。每个受试者执行280次实验,其中训练集的试验次数分别为168,224,84,56 和28,而剩下的实验数据作为测试集。

2 方法

2.1 高斯过程分类

高斯过程(Gaussian Process)是指任意时刻点集的联合概率密度都服从高斯分布的随机过程[15]。高斯过程可以看作是对高斯分布的特殊推广,只是前者是基于向量,而后者是针对函数。所以,高斯过程也像高斯分布一样,完全由它的均值和协方差确定。

简言之,高斯过程分类就是通过建立高斯过程模型得到后验概率以实现对样本特征的类别判断。其中,高斯过程模型的建立主要由潜变量函数(Latent Function)的定义、似然函数的定义以及潜变量函数后验概率计算三部分组成[16]。

对于脑电样本集D={(xi,yi),i=1,2,…,m},xi,为脑电特征样本,yi为类别标签,取值范围为{1,-1},m为特征值个数,可定义潜函数f(x)来描述xi和yi的映射关系:

p(y=1|x)=φ[f(x)]

(1)

式中:φ为累积高斯(CumulativeGaussian)函数,一般取Sigmoid函数[16],以保证概率值落在[0,1]区间。f(x)服从高斯过程,可表示为f(x,θ)～GP(0,K)。该高斯过程均值为0,K为正定协方差函数,也叫核函数,θ为核函数K的参数。由于潜函数的观测数据是相互独立的伯努利分布变量,其似然函数为:

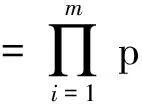
(2)

潜函数f(x)的先验分布可描述为:

p(f|x,θ)=N(0,K)

(3)

式中:K为核函数,θ为超参数,在高斯建模的训练学习过程中选择合适的核函数和最优超参数尤为重要,因为它们影响高斯过程分类器的性能。最常用的核函数为高斯核函数,可表示为:

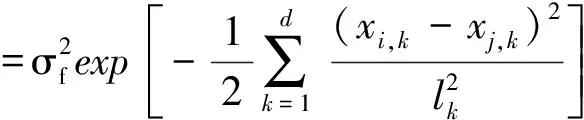
(4)

式中:σf和lk共同组成超参数θ,d表示数据的维数。σf为潜函数的幅值,用于衡量局部相关的程度。lk为长度尺度(LengthScale),用于衡量第k维数据两两之间的相关性。确定了潜函数的先验分布和似然函数,则可以根据贝叶斯公式,得到潜函数f(x)的后验分布:

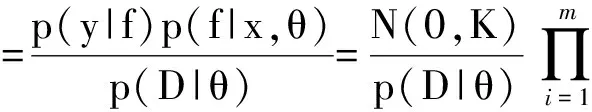
(5)

对于给定的测试样本x*,可以计算与之对应的潜函数f*的条件概率:p(f*|D,θ,x*)=∫p(y*|f,x,θ,x*)p(f|D,θ)df

(6)

进一步得到测试样本x*的类别判断概率y*:

p(y*|D,θ,x*)=∫p(y*|f*)p(f*|D,θ,x*)df

(7)

值得注意的是,由于定义的似然函数p(y|f)为Sigmoid函数,所以不能通过求解得到潜函数的后验分布和类别判断概率。针对此问题,可以采用近似逼近的方法取代原来的后验分布值进行计算,得到对应样本的类别概率。

2.2 人工蜂群算法

人工蜂群算法(ArtificialBeeColony,ABC)[17-18]是受蜂群协作采蜜行为启发而提出的一种群智能算法。该算法的生物学依据是:雇佣蜂,观察蜂和侦察蜂通过信息交流和角色转换的方式完成在不同自然环境下的采蜜。由于该算法原理简单,易于实现,适应性强,所以它引起了广大学者的关注,并被成功用于优化问题中[18]。

人工蜂群算法是一个迭代寻优的过程。对于具体的优化问题,生物学中蜂群采蜜行为涉及的因素被抽象为相应的变量,信息交流行为被抽象为相应的算法控制。其中,蜜源被抽象为潜在解,蜜源的数量即为解空间的大小,蜜源的质量好坏对应解的适应度的高低。雇佣蜂发现蜜源并分享信息的行为被抽象为潜在解的搜寻和适应度计算。观察蜂根据雇佣蜂提供的信息选择蜜源的行为被抽象为:根据适应度的概率公式进行轮盘赌选择,以提高算法收敛速度。雇佣蜂在蜜源质量没有改善时,则放弃现有蜜源,本身转变为侦察蜂的行为,被抽象为:潜在解经过多次迭代到达阈值却没得到改善,则放弃当前解,以避免算法陷入局部最优解。另外,在算法实现时,在不影响算法的思想的前提下,自然采蜜的行为细节被理想化。即假设雇佣蜂和观察蜂数目相等均为蜂群种族大小的一半,等于蜜源的数量,且同一时间内一个蜜源只被一只引领蜂开采[17]。

针对给定的寻优问题,人工蜂群算法的具体步骤如下:

①初始化:初始化蜂群大小为CS,目标函数最大评估次数为MCN,最大不更新次数为Limit,待优化参数个数为Dim,待优化参数的上下限分别为ub,lb。则解空间大小为CS,雇佣蜂和观察蜂的个数为CS/2。初始化解为:

xij=lb+rand(ub-lb)

(8)

式中:rand表示范围为[0,1]的均匀随机分布,i∈{1,2,…,CS},j∈{1,2,…,Dim}。

②雇佣蜂搜寻新解:雇佣蜂在初始解xij邻域产生新的解vij:

vij=xij+φ(xij-xkj)

(9)

式中:i≠k,φ=(rand-0.5)×2,即为范围为[-1,1]的均匀随机分布。通过目标函数和适应度函数计算出初始解和新解的适应度,如果新解的适应度高于初始解,则用新解代替初始解,否则不取代。

③观察蜂选择解:观察蜂根据雇佣蜂传递的解和适应度信息计算选择解的概率:

(10)

式中:fiti表示第i解的适应度。观察蜂根据轮盘赌的方式选择解。接着观察蜂在所选解周围的邻域周围产生新解,计算选择解和新解的适应度后,依据贪心算法在新解和原选择解之间选择解。

④侦察蜂出现:如果某些解经过Limit次循环后,解的质量没有改善,则雇佣蜂转换角色为侦察蜂,放弃该解并随机产生新解,且将迭代次数置0。

⑤结束算法:判断迭代次数是否达到MCN,若未达到,则算法正常进行,否则结束算法,输出最优解。

2.3 人工蜂群优化高斯过程算法

如前所述,人工蜂群算法是一种基于全局搜索的群智能算法,具有操作简单,搜索精度较高和鲁棒性较强的优点。利用ABC优化GPC,确定最优的核函数构建模型,能使GPC表现出更优越的性能。

使用ABC-GPC算法时,高斯过程的核函数选择如式(4),人工蜂群主要用来优化高斯过程核函数的超参数σf和lk。但是,由于σf主要影响信号的幅值,而高斯分类的输出结果被Sigmoid函数限定在[0,1]范围内,所以σf对分类结果并没有大的影响[19],可以把σf值设为1。所以,本文使用人工蜂群只对参数lk进行优化以提升分类精度。

由于优化高斯过程分类核函数中超参数的目的是为了获得更高的分类准确率,所以依据人工蜂群中选择适应度函数的基本形式,在脑电信号模式分类时选取的适应度函数为:

(11)

式中:acc为脑电训练特征样本送入高斯过程分类器得到的分类正确率。

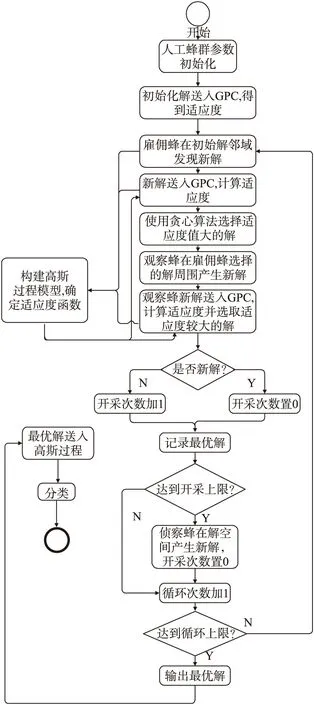
图1 人工蜂群优化高斯过程算法流程

对于给定的运动想象脑电数据,基于人工蜂群优化的高斯过程分类算法的流程如图1所示。

具体算法步骤如下:①根据高斯过程参数优化需求,初始化人工蜂群算法的控制参数;②将人工蜂群的初始解和脑电训练特征样本集送入高斯过程分类器,得到分类准确率,进一步计算适应度;③雇佣蜂在初始解周围产生新解,计算适应度,然后根据贪心算法,在新解和初始解中选择确定的解;④观察蜂从雇佣蜂处得到解并通过轮盘赌的方式选择解,并计算适应度和生成新解,根据贪心算法确定优化解;⑤侦察蜂出现以避免算法陷入局部最优;⑥人工蜂群算法迭代结束,将求得的最优解保存;⑦将脑电测试特征样本集送入高斯过程分类器,将上一步保存的最优解送入核函数,即可得到最后的分类结果。

2.4 基于优化高斯过程的脑电分类

根据脑电信号易受噪声干扰以及非线性等特点,对运动想象脑电信号的处理主要包括预处理、特征提取和分类阶段。

①预处理:巴特沃斯滤波器是数字带通滤波器的一种,由于其实现简单,滤波效果显著,所以在运动想象脑电信号的预处理中得到广泛应用[20],受试者进行运动想象时,大脑中心区域会产生8 Hz～12 Hz的mu节律和18 Hz～25 Hz的beta节律,本文使用8 Hz～30 Hz[21]的5阶巴特沃兹滤波器对脑电数据进行滤波。

②特征提取:共同空间模式CSP(Common Spatial Pattern)算法是一种广泛用于脑电信号处理的特征提取方法[21]。CSP算法对协方差矩阵同时联合对角化,寻找一组空间滤波器,使经过它滤波投影后的信号中一类信号的方差最大,另一类信号的方差最小,从而最大化类间样本的距离。本文使用CSP提取脑电信号的特征向量。在实验中,CSP的滤波器个数m取3。

③分类:对于提取出的脑电特征数据,分别使用支持向量机(SVM)、基于人工蜂群优化的支持向量机(ABC-SVM)、高斯过程分类器(GPC)、基于人工蜂群优化的高斯过程分类器(ABC-GPC)对不同任务下的脑电特征向量进行识别和比对分析。其中,采用ABC-GPC时,人工蜂群算法的适应度函数如式(11),参数设置如表1所示。

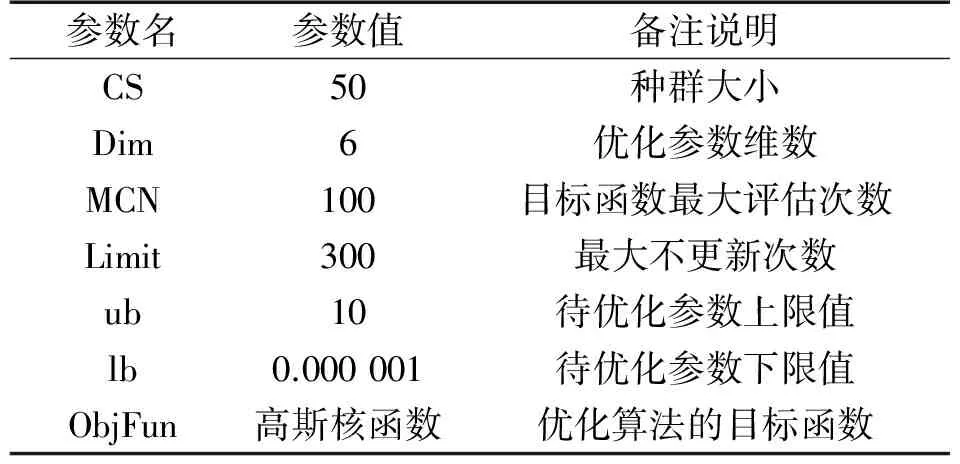
表1 人工蜂群的参数设置

3 实验结果与分析

为了证明方法的有效性,本文采用两个实验:实验一是用来表明人工蜂群算法及其他优化算法的性能优劣;实验二是对比人工蜂群优化的高斯过程分类方法用于脑电信号的分类时,与其他常用或者优化过的分类方法的优劣。

3.1 优化算法实验

为了评估人工蜂群算法的性能,选择函数优化领域中两个具有代表性的标准测试函数进行测试。表2给出了所选择函数的表达式及相应特性。

表2 测试函数

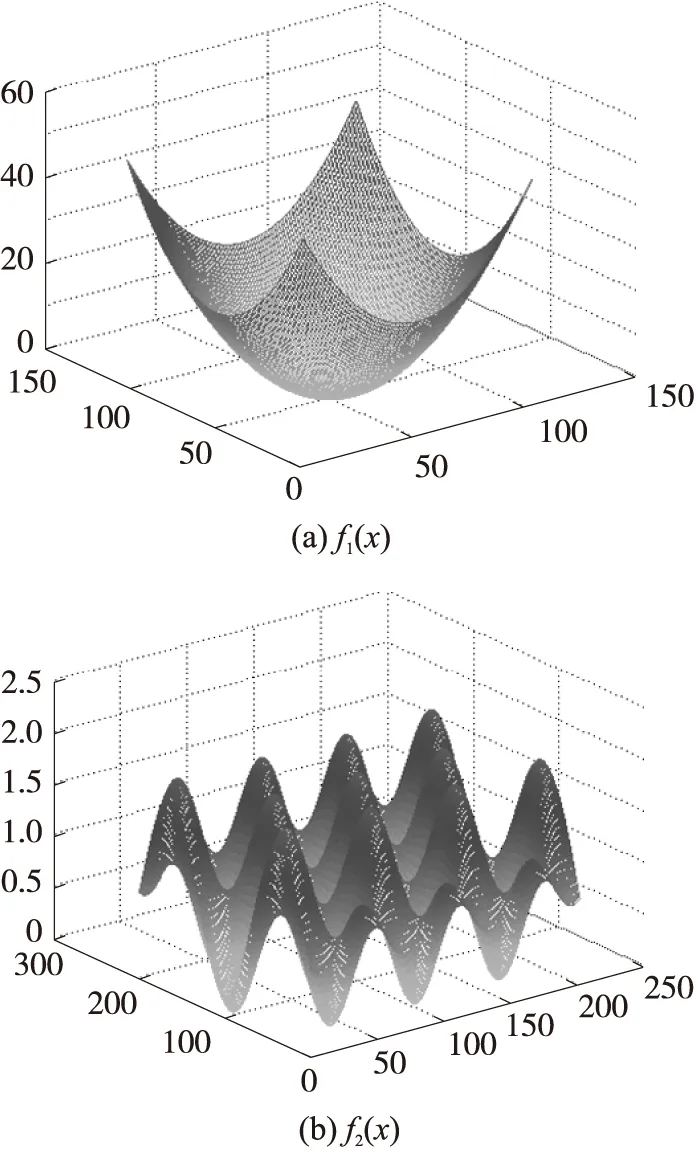
图2 测试函数三维波形图

在表2中f1(x)为连续性单模态函数,只有一个全局最小值没有局部最小值,用来测定算法的寻优精度,f2(x)为复杂的多模态模型,有多个局部最小值,全局最优值难以确定,所以可用来验证算法是否易陷入局部最优。为了更直观的说明两个函数的特点,做出函数的三维波形图如图2所示。

分别用遗传算法、粒子群算法和人工蜂群算法对上面所提测试函数求最优值。其中,粒子群和人工蜂群算法的参数设置依据参考文献[22],遗传算法的种群规模取100,最大迭代次数为100 000,交叉概率为0.5,变异概率为0.045,竞赛规模为10。每种算法重复实验30次,将30次最优值的平均值记录如下表。为了简化表示,当数值小于10-12时,则将该值记作0值。上面3种算法的最优值结果如表3所示。

表3 优化算法的最优值结果

观察表3的实验结果,可以发现:对于函数f1(x)3种算法的寻优性能,人工蜂群优于粒子群,粒子群优于遗传算法,说明人工蜂群的优化精度最高。对于函数f2(x),粒子群算法最优值求取结果不仅差于人工蜂群算法和遗传算法,且与实际最优值有较大差距,说明该算法可能已陷入局部最优值。遗传算法较粒子群算法表现出较好的全局寻优能力,而人工蜂群算法很好的避免了此问题,所以本文提出使用人工蜂群算法优化高斯过程分类器的方法。

3.2 脑电分类实验

为了说明所提算法的有效性,本文采用BCI Competition Ⅳ Data Set 1和BCI Competition Ⅲ Data Set Ⅳa两组数据集对所提分类算法进行验证。

3.2.1 数据集Data Set 1

选用受试者a,b,f和g提供的4组标定数据进行实验。参照文献[20]的推荐,本文选取11个通道的脑电信号进行分析,分别对应10～20系统的“FC3”,“FC4”,“Cz”,“C3”,“C4”,“C5”,“C6”,“T7”,“T8”,“CCP3”,“CCP4”,时间段选取4 s,每个受试者执行200次实验,每类任务执行100次,从200次实验中随机取120次用于训练学习,80次用作测试集。

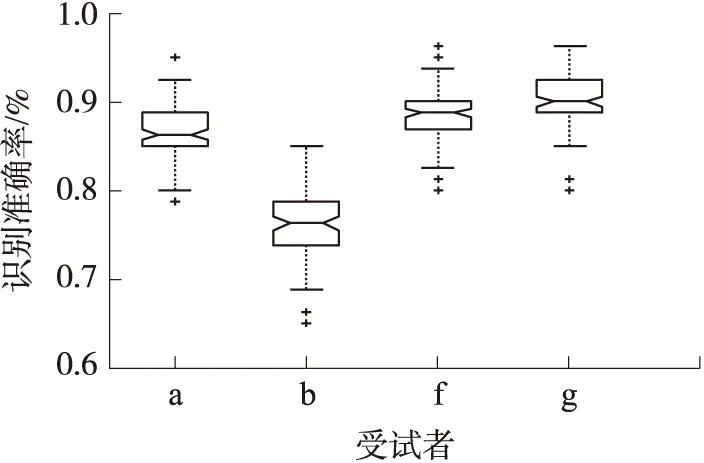
图3 ABC-GPC方法100次分类实验准确率统计

为了使实验结果更直观,将本文所提的分类方法得出的分类准确率统计结果以箱线图的方式画出,如图3所示。其中,箱线图的两端分别表示分类过程重复进行100次迭代后准确率的上下四分数,中线表示准确率的中位数,“+”表示温和异常点。

观察图3可知,除了受试者b的准确率略低外,其他3名受试者的中位线都在0.85以上,说明平均准确率结果都高于85%,其中最高准确率接近92%。

为了进一步说明所提方法的效果,将4种分类方法的分类过程重复试验100次,并统计平均准确率和标准差如图4所示。图4中,柱状图表示平均准确率,柱状图上的短线表示标准差。

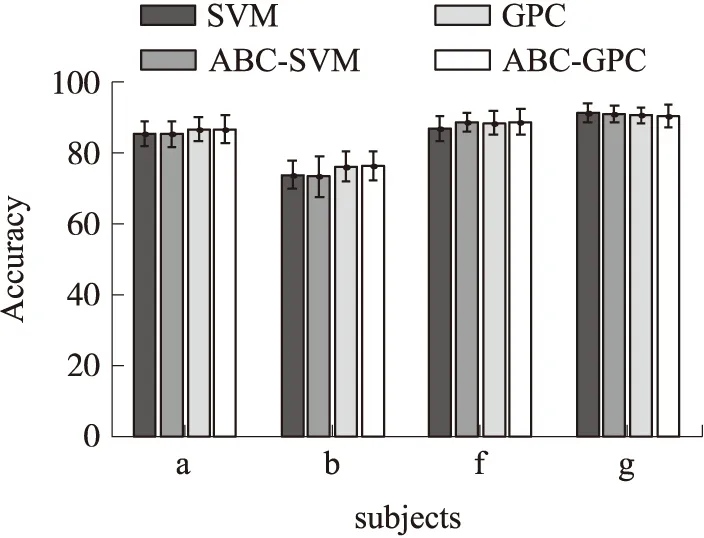
图4 数据集Data Set 1中不同受试者的分类准确率

从图4中可以看出,不同的分类方法对于不同受试者的分类性能优劣不同。图4中对于受试者b和f,ABC-GPC算法的平均准确率相对传统GPC方法分别提高了0.2%、0.3%;对于受试者a,这两种方法分类准确率接近,且都高于SVM和ABC-SVM;对于受试者g,ABC-GPC略低于其他3种方法,总体而言ABC-GPC算法比其他3种分类算法具有相对更好的分类性能。

3.2.2 数据集Data Set Ⅳa

本文选用aa,av,ay 3个受试者,他们的实验次数如表4所示。

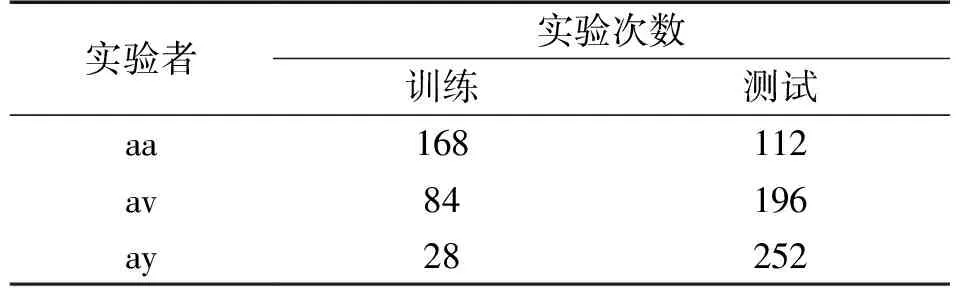
表4 3个受试者实验次数说明

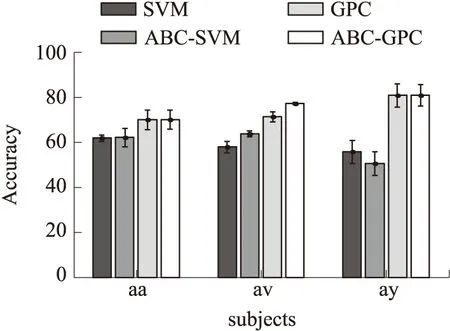
图5 数据集Data Set IVa中不同受试者的分类准确率

图5给出的分类结果,不管是对于受试者个体还是平均值而言,GPC类方法的分类准确率都优于SVM和ABC-SVM,这可能是因为该数据集主要是小样本数据,说明GPC类方法在处理小样本问题时,表现出比SVM更好的性能。另外,ABC-GPC法的平均准确率比传统GPC方法高2%,尤其是在受试者av上表现出了明显优越性。

4 结论

模式分类是运动想象EEG信号识别不同想象任务的关键环节之一。高斯过程算法虽然分类优势明显并且被广泛的研究,但是该算法具有优化迭代次数不确定,容易陷入局部最优的局限性。本文提出了人工蜂群算法优化高斯过程的运动想象脑电信号分类方法。使用人工蜂群优化高斯过程的超参数,以克服传统高斯过程超参数的优化迭代次数不确定,且易陷入局部最优的特点。使用两组脑电竞赛数据集对所提方法进行实验,并与SVM、ABC-SVM以及传统高斯过程方法进行对比,结果表明本文方法能较好地对脑电信号进行分类,因此该方法可以作为一种有效的脑电信号分类方法。然而,本文所提的分类方法在使用人工蜂群优化参数时,耗时较大,这是后期算法研究需要改进的地方。

[1] Marchetti M,Priftis K. Brain-Computer Interfaces in Amyotrophic Lateral Sclerosis:A Metanalysis[J]. Clinical Neurophysiology,2015,126(6):1255-1263.

[2] Chen W,Shen C P,Chiu M J,et al. Epileptic EEG Visualization and Sonification Based on Linear Discriminate Analysis[C]//Proceedings of IEEE Conference on Engineering in Medicine and Biology Society,Milan,2015:4466-4469.

[3] Zuhair M,Thomas S,Keshri A K,et al. Automatic Identification of an Epileptic Spike Pattern in an EEG Signals Using ANN[C]//Proceedings of the 3rd International Conference on Soft Computing for Problem Solving,India,2014:915-923.

[4] Brinkmann B H,Patterson E E,Vite C,et al. Forecasting Seizures Using Intracranial EEG Measures and SVM in Naturally Occurring Canine Epilepsy[J]. PloS One,2015,10(8):e0133900.

[5] 王金甲,贾敏. 辅助训练的半监督线性支持向量机用于EEG分类[J]. 仪器仪表学报,2013,34(4):768-773.

[6] 张毅,祝翔,罗元,等. 基于SVM多分类技术的肌电辅助脑电智能轮椅控制系统[J]. 中南大学学报(自然科学版),2013,S2:73-76.

[7] Rasmussen C E,Williams C K I. Gaussian processes for machine learning[M]. The MIT press,Cambridge,2006.

[8] 夏战国,夏士雄,蔡世玉,等. 类不均衡的半监督高斯过程分类算法[J]. 通信学报,2013,34(5):42-51.

[9] 何志昆,刘光斌,赵曦晶,等. 高斯过程回归方法综述[J]. 控制与决策,2013,28(8):1121-1129.

[10] 刘开云,方昱,刘保国,等. 隧道围岩变形预测的进化高斯过程回归模型[J]. 铁道学报,2011,33(12):101-106.

[11] 徐冲,刘保国,刘开云,等. 基于粒子群-高斯过程回归耦合算法的滑坡位移时序分析预测智能模型[J]. 岩土力学,2011,32(6):1669-1675.

[12] 张乐,刘忠,张建强,等. 基于人工蜂群算法优化的改进高斯过程模型[J]. 国防科技大学学报,2014,36(1):154-160.

[13] Blankertz B,Dornhege G,Krauledat M,et al. The Non-Invasive Berlin Brain-Computer Interface:Fast Acquisition of Effective Performance in Untrained Subjects[J]. NeuroImage,2007,37(2):539-550.

[14] Dornhege G,Blankertz B,Curio G,et al. Boosting Bit Rates in Non-Invasive EEG Single-Trial Classifications by Feature Combination and Multi-Class Paradigms[J]. IEEE Transactions on Biomedical Engineering,2004,51(6):993-1002.

[15] Wang B,Wan F,Mak P U,et al. EEG Signals Classification for Brain Computer Interfaces Based on Gaussian Process Classifier[C]//Proceedings of IEEE Conference on Information,Communications and Signal Processing,Macau,2009:1-5.

[16] 贺建军,张俊星,贾思齐,等. 一种新高斯过程分类算法[J]. 控制与决策,2014,29(9):1587-1592.

[17] Karaboga D. A Idea Based on Bee Swarm for Numerical Optimization[R]. Türkiye:zErciyes University,Engineering Faculty,Computer Engineering Department,2005.

[18] Sharma M,Chandra S. Application of Artificial Bee Colony Algorithm for Numerical Optimization Technique[C]//Proceedings of IEEE Conference on Advance Computing,Banglore,2015:1267-1272.

[19] Wang L,Li C. Spectrum-Based Kernel Length Estimation for Gaussian Process Classification[J]. IEEE Transactions on Cybernetics,2014,44(6):805-816.

[20] Samek W,Kawanabe M,Muller K R. Divergence-Based Framework for Common Spatial Patterns Algorithms[J]. IEEE Transactions on Biomedical Engineering,2014(7):50-72.

[21] Park C,Looney D,Ahrabian A,et al. Classification of Motor Imagery BCI Using Multivariate Empirical Mode Decomposition[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering,2013,21(1):10-22.

[22] Karaboga D,Basturk B. On the Performance of Artificial Bee Colony(ABC)Algorithm[J]. Applied Soft Computing,2008,8(1):687-697.

耿雪青(1990-),女,山西阳泉人,硕士,从事脑电信号处理与分析方面的研究,1565782139@qq.com;

佘青山(1980-),男,湖北荆州人,副教授,博士,从事生物信息处理与分析、机器学习、模式识别等领域的研究,qsshe@hdu.edu.cn;

韩 笑(1991-),女,河南南阳人,硕士,从事脑电信号处理与分析方面的研究,754163862@qq.com。

Classification of Motor Imagery EEG Based on Gaussian Process Optimized with Artificial Bee Colony*

GENGXueqing,SHEQingshan*,HANXiao,MENGMing

(Institute of Intelligent Control and Robotics,Hangzhou Dianzi University,Hangzhou 310018,China)

The conjugate gradient method is used to determine the parameters in the traditional Gaussian process. However,the conjugate gradient method has a strong dependence on the initial value and is easy to fall into local optimum. In order to solve the problem,a Gaussian process classification(GPC)method is proposed based on artificial bee colony(ABC)optimization and applied for pattern recognition of EEG signals. Firstly,Gaussian process model is constructed,and suitable kernel function is chosen and the parameters to be optimized are specified. Then the reciprocal of the recognition error rate is selected as fitness function,and the parameters which are used to obtain optimal accuracy in a limited range are found out by employing the ABC algorithm. Finally,the Gaussian process classifier with optimized parameters is used to classify the samples. The efficiency of the propose method has been demonstrated by comparison with support vector machine(SVM),support vector machine optimized with Artificial bee colony(ABC-SVM)and GPC algorithms on both BCI Competition Ⅳ Data Set 1 in 2008 and BCI Competition Ⅲ Data Set Ⅳa in 2005.

EEG signal,Gaussian process classification,artificial bee colony,motor imagery

项目来源:浙江省自然科学基金资助项目(LY15F010009,LY14F030023);国家自然科学基金资助项目(61201302)

2016-07-01 修改日期:2016-11-18

TP391

A

1004-1699(2017)03-0378-07

C:7230

10.3969/j.issn.1004-1699.2017.03.008